VECTOR ALGEBRA
SCALARS AND VECTORS
- A quantity which has only magnitude and not related to any direction is called a scalar quantity. For example, the quantities such as mass, length, time, temperature, area, volume, speed, density, work etc. are measured by their magnitude only.
- A quantity which has magnitude and also a direction in space is called a vector quantity. For example, the quantities such as displacement, velocity, acceleration, force, torque, etc. must be described by magnitude as well as direction.
REPRESENTATION OF VECTORS
- Vectors are represented by directed line segments. A vector
is represented by the directed line segment PQ such that
- the magnitude of vector
is equal to PQ and
- the direction of vector
is along the line from P to Q.
- The vector
, represented by the directed line segment PQ, is denoted by
and read as 'vector PQ'. The points P and Q are respectively called the initial point and the terminal point of the vector
.
- The magnitude of the vector
is denoted by |
| or simply by PQ and is equal to the distance between the points P and Q. The magnitude of a vector is also called the length or its modulus.
TYPES OF VECTORS
- Zero vector or Null Vector : A vector is called a zero vector if its initial and terminal points are identical. The magnitude of a zero vector is zero and the direction indeterminate. Zero vector is denoted as
. For example
, is a zero vector with identical initial and terminal point P.
- Equal vectors : Two non-zero vectors are said to be equal vectors if their magnitudes are equal and directions are same i.e., they act parallel to each other in the same direction.
In the adjoining figure, vectors and are equal. All zero vectors are defined to be equal vectors.
- Collinear vectors : Two or more non-zero vectors are said to be collinear vectors if these are parallel to the same line.
Thus, non-collinear vectors are vectors which are not parallel to the same line. Hence, when their initial points coincide, they do not lie on the same line.
- Like and unlike vectors : Parallel Vectors are said to be like vectors if they have same direction and unlike vectors, if they have opposite directions.
The equal vectors are like vectors, but like vectors, may not be equal vectors.
- Unit vector : A vector is called a unit vector if its magnitude is equal to one. The sign '^' is used for a unit vector. Thus, denotes a unit vector.
- Localised vector : A vector is called a localised vector if it has a specified initial point.
- Free vector : A vector is called a free vector if it does not have any specific initial point, and can be shifted anywhere in space keeping it parallel and direction unchanged with respect to original position. In general we assume all vectors as free vectors unless stated otherwise.
- Negative of a vector : The negative of a vector is defined as the vector having the same magnitude but opposite direction. For example, if
, then the negative of
is the vector
and is denoted as –
.
- Coplanar vectors : Two or more non-zero vectors are said to be coplanar vectors if these are parallel to the same plane.
Thus, non-coplanar vectors are vectors which are not parallel to the same plane. Hence, when their initial points coincide, they do not lie in the same plane.
ADDITION OF VECTORS
Let  and
and  be any two vectors. From the terminal point of
be any two vectors. From the terminal point of  , vector
, vector is drawn. Then, the vector from the initial point O of
is drawn. Then, the vector from the initial point O of  to the terminal point B of
to the terminal point B of  is called the sum of vectors
is called the sum of vectors  and
and  and is denoted by
and is denoted by  +
+ . This is called the triangle law of addition of vectors.
. This is called the triangle law of addition of vectors.
The vectors are also added by using the following method. Let  and
and be any two vectors. From the initial point of
be any two vectors. From the initial point of , vector
, vector  is drawn. Let O be their common initial point. If A and B be respectively the terminal points of
is drawn. Let O be their common initial point. If A and B be respectively the terminal points of  and
and  , then parallelogram OACB is completed with OA and OB as adjacent sides. The vector
, then parallelogram OACB is completed with OA and OB as adjacent sides. The vector  is defined as the sum of
is defined as the sum of  and
and  . This is called the parallelogram law of addition of vectors.
. This is called the parallelogram law of addition of vectors.
The sum of two vectors is also called their resultant, and the process of addition as COMPOSITION.
PROPERTIES OF VECTOR ADDITION
- Vector addition is commutative, i.e.,
- Vector addition is associative,
i.e., 
. So the zero vector is additive identity.
. So, the additive inverse of
is
.
ADDITION OF ANY NUMBER OF VECTORS
To find the sum of any number of vectors we represent the vectors by directed line segments with the terminal point of the previous vector as the initial point of the next vector. Then the line segment joining the initial point of the first vector to the terminal point of the last vector will represent the sum of the vectors.
Thus if
= 
If the terminal point F of the last vector coincide with the initial point of the first vector then
i.e. the sum of vectors is a zero or null vector in this case.
DIFFERENCE OF VECTORS
If  and
and  be any two vectors, then their difference
be any two vectors, then their difference  is defined as
is defined as  .
.
MULTIPLICATION OF A VECTOR BY A SCALAR
If  be any vector and m any scalar, then the multiplication of
be any vector and m any scalar, then the multiplication of  by m is defined as a vector having magnitude | m | |
by m is defined as a vector having magnitude | m | | 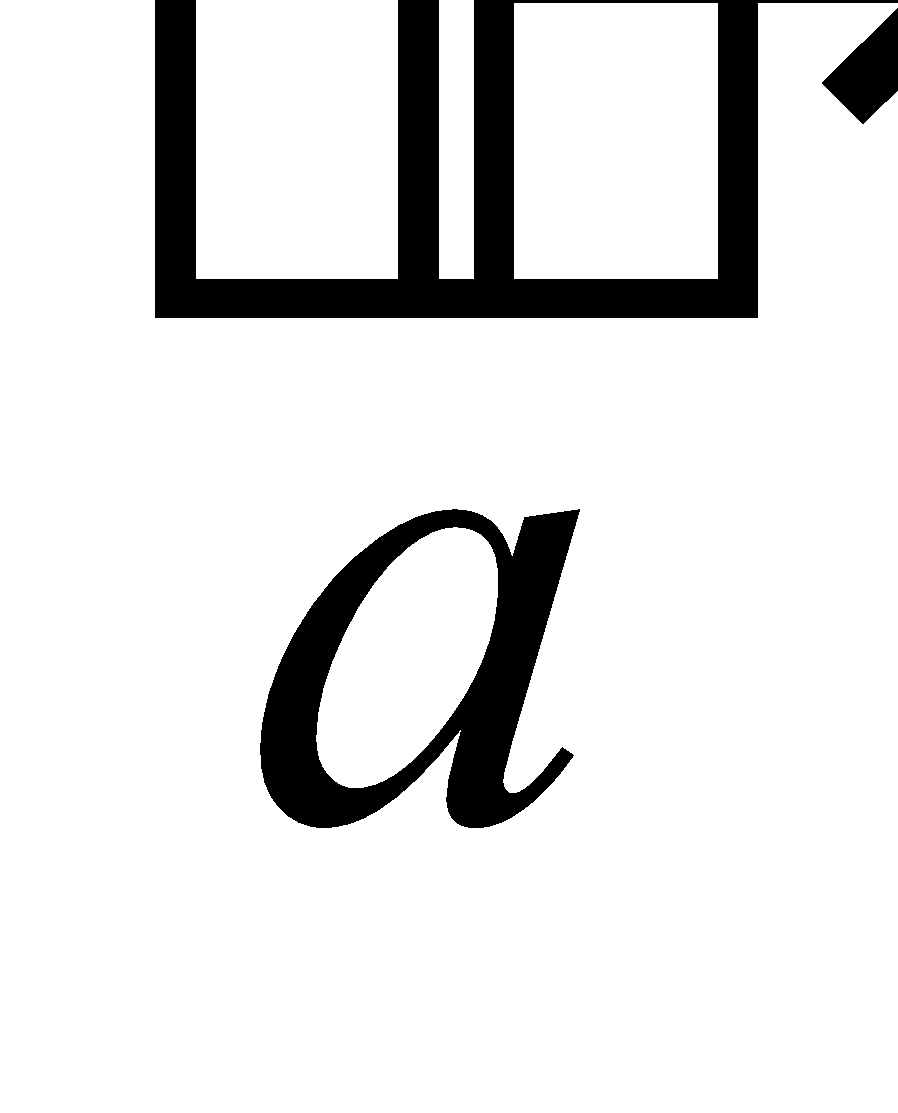 | and direction same as of
| and direction same as of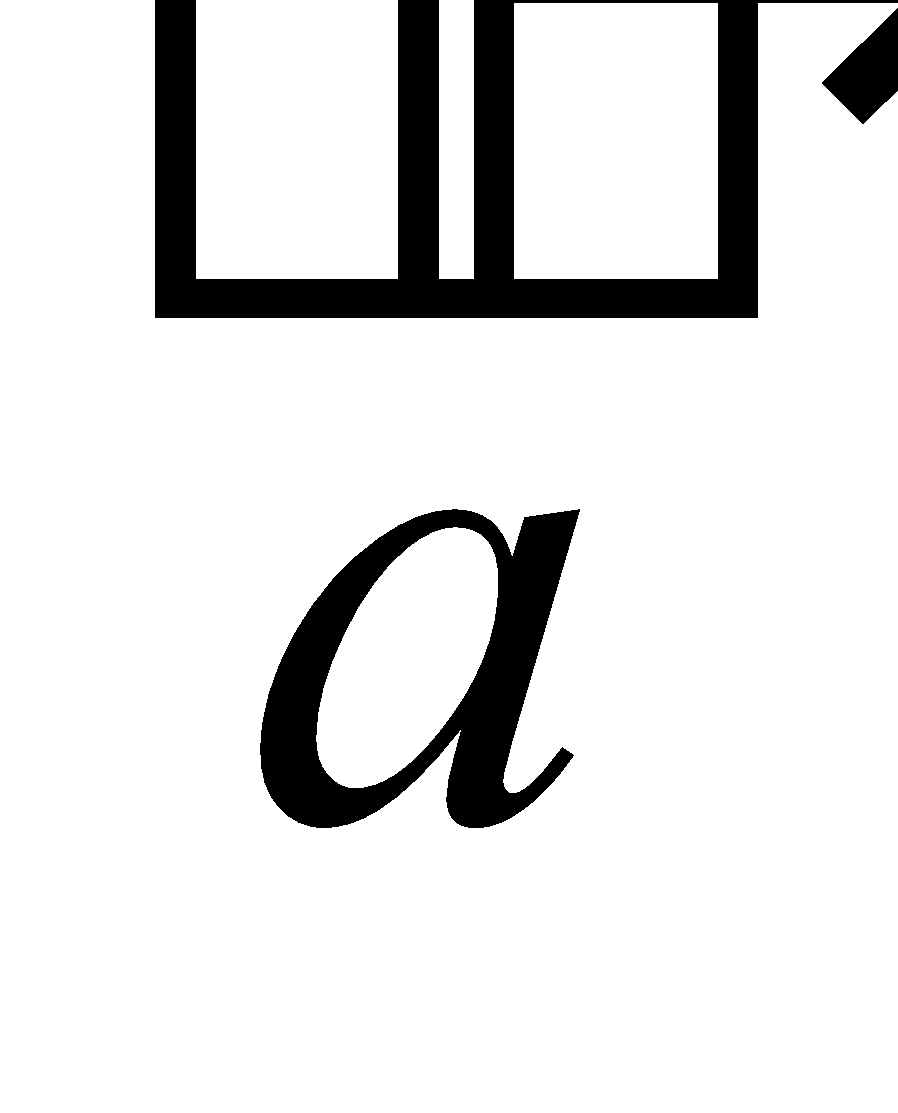 , if m is positive and direction reversed, if m is negative. The product of
, if m is positive and direction reversed, if m is negative. The product of  and m is denoted by . If m
and m is denoted by . If m  = 0, then
= 0, then is the zero vector.
is the zero vector.
For example,
if 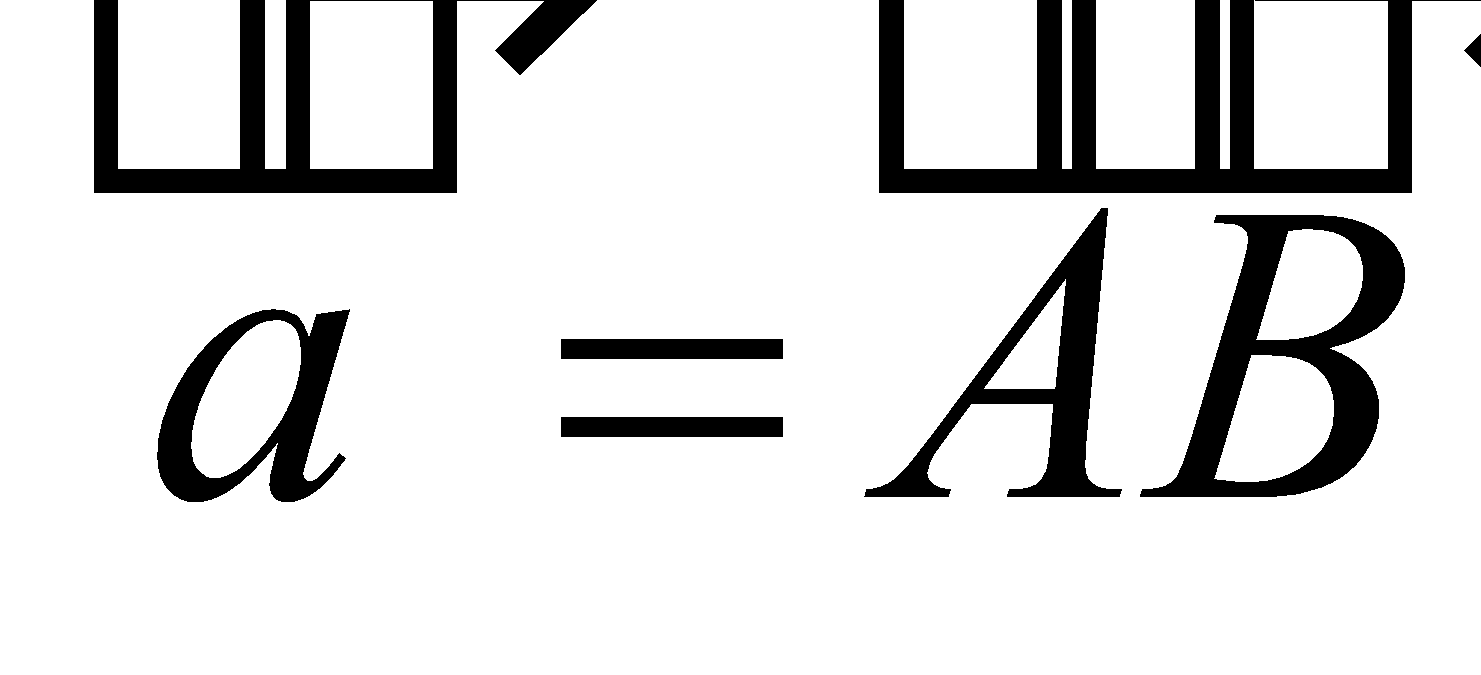 , then
, then and direction same as that of
and direction same as that of  . The magnitude of the vector –3
. The magnitude of the vector –3  = 3 |
= 3 | | and direction opposite as that of
| and direction opposite as that of .
.
PROPERTIES
- If m and n are scalars
and any vector, then
and
- If m is any scalar and
and
any vectors, then
- For any vector
POSITION VECTOR OF A POINT
The position vector of a point P with respect to a fixed point, say O, is the vector  . The fixed point is called the origin.
. The fixed point is called the origin.
Let  be any vector. We have
be any vector. We have
A given vector can be expressed as "position vector of the terminal point minus position vector of the initial point".
COLLINEAR VECTORS
Vectors  and
and  are collinear iff
are collinear iff  , for some non-zero scalar
, for some non-zero scalar  .
.
COLLINEAR POINTS
Let A, B, C be any three points.
A, B, C are collinear  are collinear vectors.
are collinear vectors.
LINEAR COMBINATION OF VECTORS
Let  be vectors and x, y, z, ..... be scalars then the expression
be vectors and x, y, z, ..... be scalars then the expression  is called a linear combination of vectors
is called a linear combination of vectors  .
.
If 
Then the vector  is said to be a linear combination of vectors
is said to be a linear combination of vectors  .
.
LINEARLY INDEPENDENT AND DEPENDENT SYSTEM OF VECTORS
- The system of vectors
is said to be linearly dependent if there exists a system of scalars x, y, z, ..... not all zero such that
- The system of vectors
is said to be linearly independent if
.
THEOREMS
- Two non-collinear vectors
and
are linearly independent.
- Three non-coplanar vectors
are linearly independent.
- More than three vectors are always linearly dependent.
RESOLUTION OR COMPONENTS OF A VECTOR IN A PLANE
- Let
and
be any two non-collinear vectors, then any vector
coplanar with
and
, can be uniquely expressed as
, where x and y are scalars.
- Let
and
be unit vectors along two perpendicular directions OX and OY respectively in a plane. These are called basic unit vectors (or Basis).
Let P(x, y) be any point in the plane
The vectors  and
and  are called the component vectors of
are called the component vectors of along X-axis and Y-axis respectively.
along X-axis and Y-axis respectively.
The component vector of  along X-axis is the
along X-axis is the vector
vector
The component vector of  along Y-axis is the vector
along Y-axis is the vector
Position vector of P(x, y) =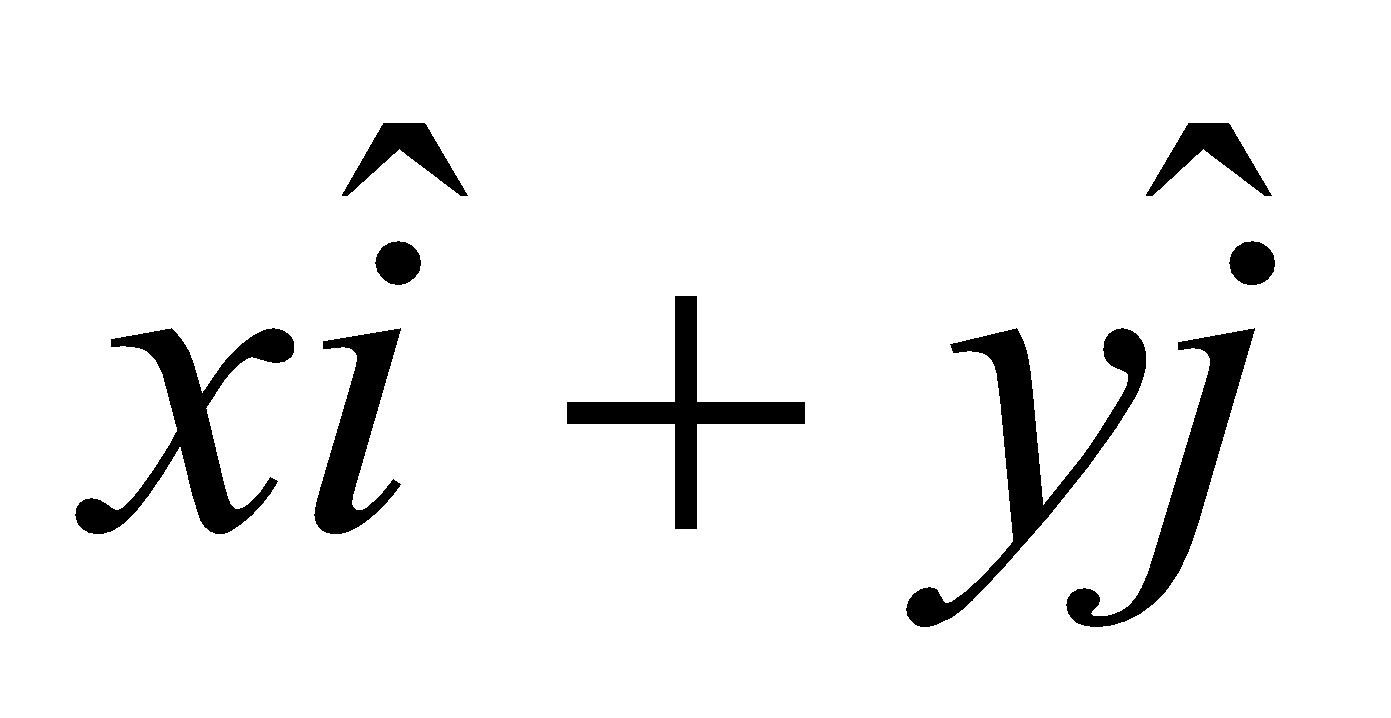 .
.
Also 
RESOLUTION OR COMPONENTS OF A VECTOR IN SPACE
Let  be three non coplanar vectors, then any vector
be three non coplanar vectors, then any vector  in space can be uniquely expressed as
in space can be uniquely expressed as  , where x, y, z are scalars,
, where x, y, z are scalars,  are the components of vector
are the components of vector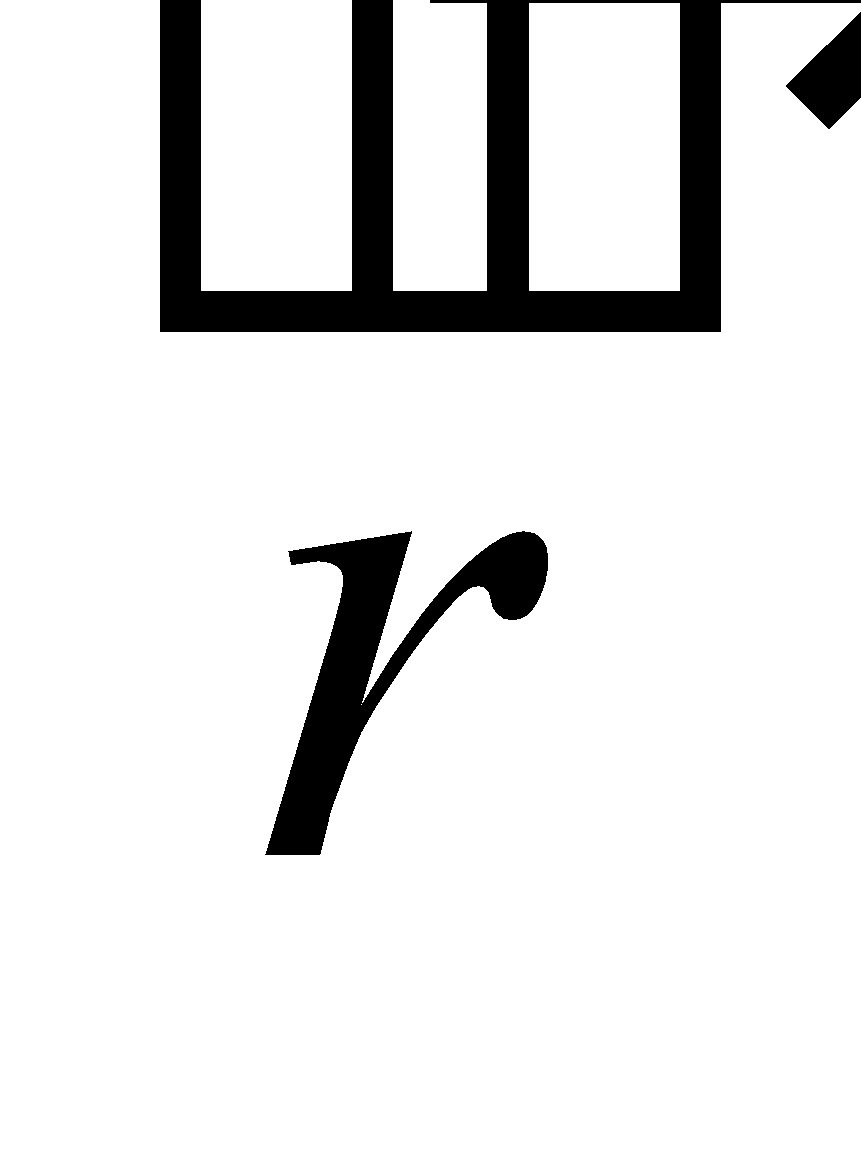 in the directions of
in the directions of  respectively.
respectively.
Let  be unit vectors along rectangular coordinate axes OX, OY and OZ respectively. These are called basic unit vectors, (or BASIS).
be unit vectors along rectangular coordinate axes OX, OY and OZ respectively. These are called basic unit vectors, (or BASIS).
Let P (x, y, z) be any point in space. From P, draw PQ perpendicular on XY-plane. From Q, draw QA and QB perpendiculars on X-axis and Y-axis respectively.
The vectors  ,
,  and
and are called the component vectors of
are called the component vectors of  along X-axis, Y-axis and Z-axis respectively.
along X-axis, Y-axis and Z-axis respectively.
The component vectors of  , along X-axis, Y-axis and Z-axis are respectively
, along X-axis, Y-axis and Z-axis are respectively ,
,  and
and  .
.  is the position vector of the point P(x, y, z).
is the position vector of the point P(x, y, z).
P.V. of P(x, y, z) = 
 .
.
Also, OP2 = OQ2 + QP2 = (OA2 + AQ2) + QP2
= OA2 + OB2 + OC2 = | x |2 + | y |2 + | z |2 = x2 + y2 + z2
Note that the components of a vector may be found in any given direction but the resolved parts are always in perpendicular directions.
SECTION FORMULA
Let be the position vectors of two points A and B respectively with respect to an origin O. Then the position vector
be the position vectors of two points A and B respectively with respect to an origin O. Then the position vector of the point P, with respect to the same origin O, which divides AB in the ratio m : n is given by
of the point P, with respect to the same origin O, which divides AB in the ratio m : n is given by
Also, 
The position vector of the midpoint of  and
and  is
is 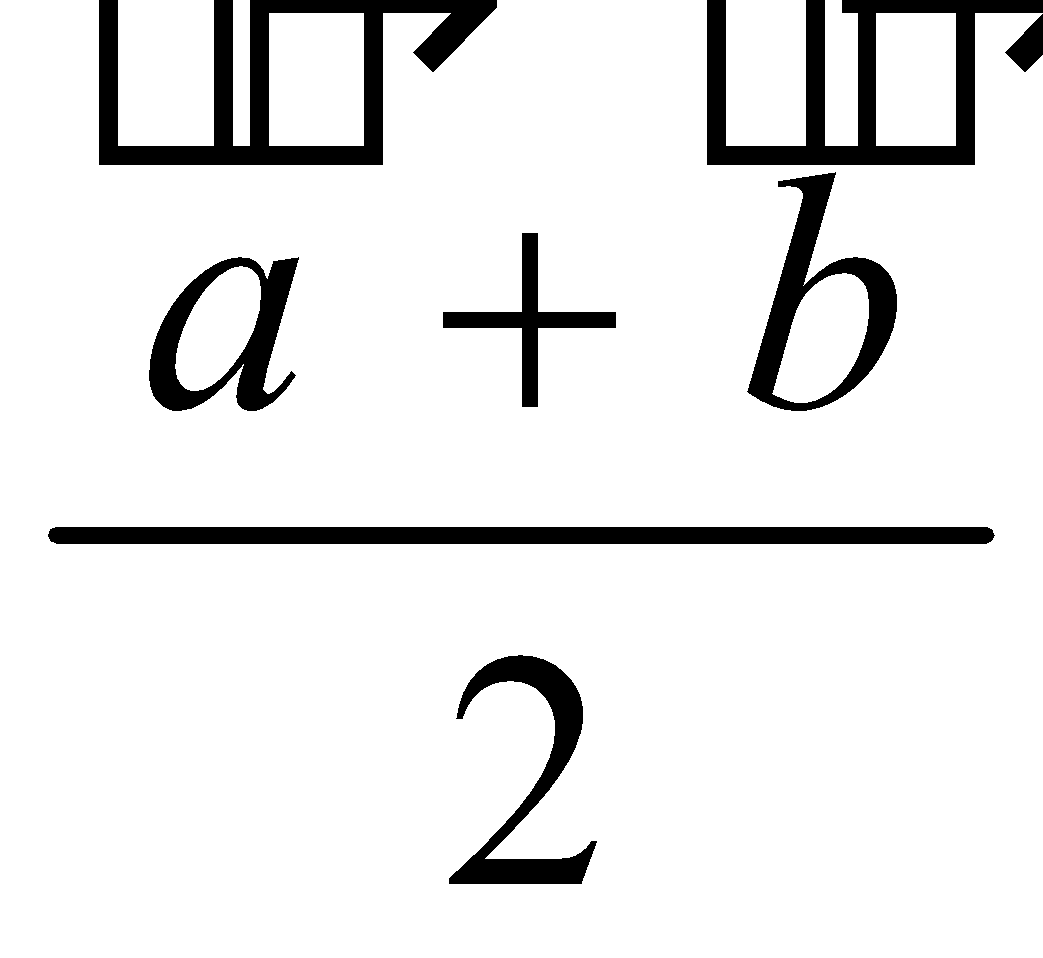 . Thus, if P is the midpoint of points A and B, then
. Thus, if P is the midpoint of points A and B, then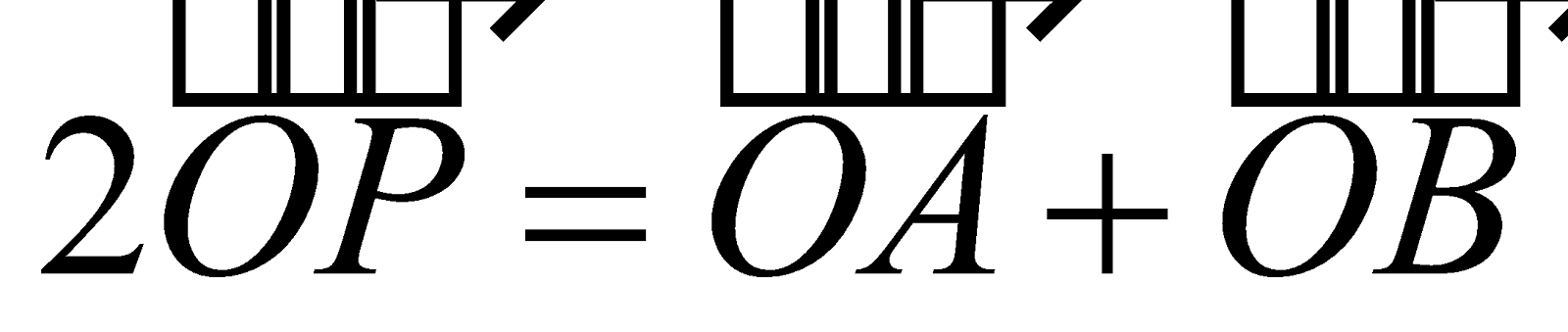 .
.
CENTROID OF A TRIANGLE
If  be P.V.'s of the vertices A, B, C of a triangle ABC respectively, then the P.V. of the centroid G of the triangle is
be P.V.'s of the vertices A, B, C of a triangle ABC respectively, then the P.V. of the centroid G of the triangle is .
.
Also, the P.V. of incentre I of is 
and the P.V. of orthocentre of is  .
.
COLLINEARITY OF THREE POINTS
The necessary and sufficient condition that three points with P.V.'s are collinear is that there exist three scalars x, y, z not all zero such that
are collinear is that there exist three scalars x, y, z not all zero such that 
COPLANARITY OF FOUR POINTS
The necessary and sufficient condition that four points with P.V.'s  are coplanar is that there exist scalar x, y, z, t not all zero such that
are coplanar is that there exist scalar x, y, z, t not all zero such that 
SCALAR PRODUCT OF TWO VECTORS
If  and
and  are two non-zero vectors then the scalar or dot product of
are two non-zero vectors then the scalar or dot product of  and
and  is denoted by
is denoted by .
. and is defined as
and is defined as 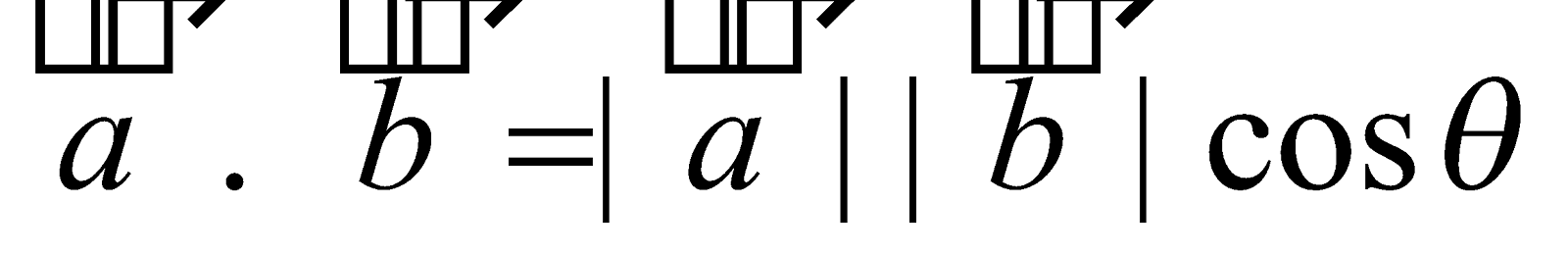
where is the angle between the two vectors and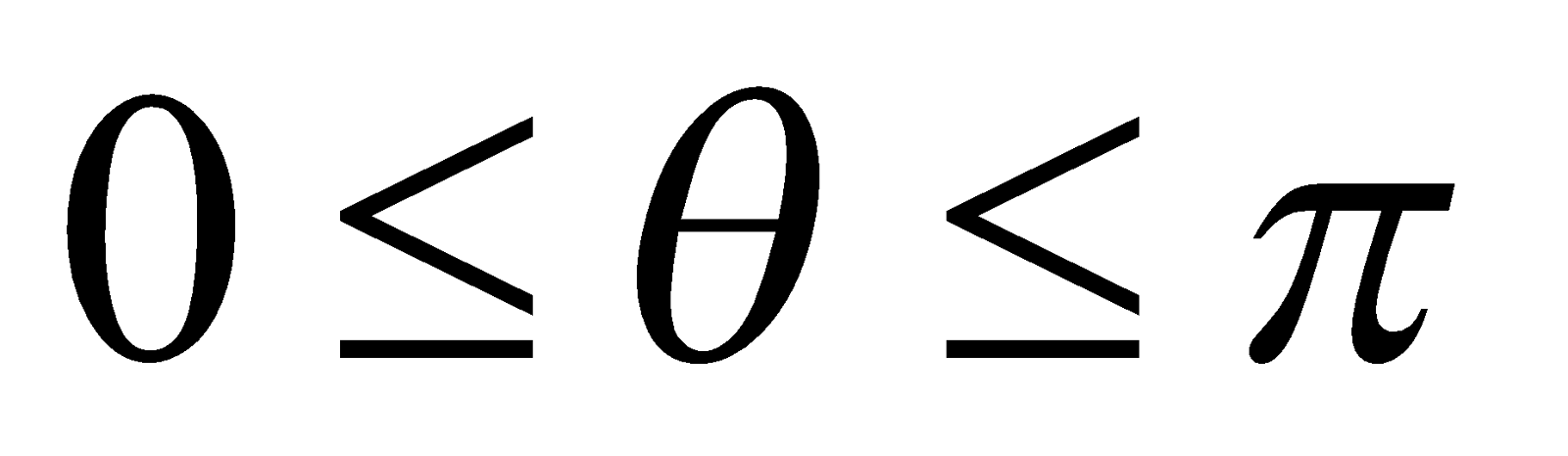 .
.
IMPORTANT POINTS
- The angle between two vectors
and
is defined as the smaller angle between them when they are drawn with the same initial point.
Usually, we take  . Angle between two like vectors is 0 and angle between two unlike vectors is .
. Angle between two like vectors is 0 and angle between two unlike vectors is .
- The dot product is a scalar quantity, since it is the product of three scalars
and
.
- If either
is the null vector, the scalar product is the scalar zero.
- If
are two unit vectors, than
. Thus, the scalar product of two unit vectors is equal to the cosine of the angle between their directions.
- Since the scalar product of two vectors is only a number, we see that (i)
is only a number being the product of two numbers
and
(ii)
is a vector whose modulus is
times that of
.
GEOMETRICAL INTERPRETATION OF SCALAR PRODUCT
Suppose the vectors and
and are represented by the directed line segments
are represented by the directed line segments and
and respectively.
respectively.
Then 
Also,
SIGN OF THE SCALAR PRODUCT
If  be the two non-zero vectors, then the scalar product
be the two non-zero vectors, then the scalar product  , is positive, negative, or zero, according as the angle , between the vectors is acute, obtuse, or right.
, is positive, negative, or zero, according as the angle , between the vectors is acute, obtuse, or right.
LENGTH OF A VECTOR AS A SCALAR PRODUCT
If be any vector, then the scalar product
be any vector, then the scalar product
CONDITION OF PERPENDICULARITY
We notice that if be any two vectors, then their scalar product
be any two vectors, then their scalar product  will vanish, if and only if, either at least one of the two vectors is the zero vector or the two vectors are at right angles to each other. Thus, the scalar product of two non-zero vectors is zero if they are at right angles to each other, and conversely.
will vanish, if and only if, either at least one of the two vectors is the zero vector or the two vectors are at right angles to each other. Thus, the scalar product of two non-zero vectors is zero if they are at right angles to each other, and conversely.
SCALAR PRODUCT IN TERMS OF COMPONENTS
In the view of definition of scalar products of vectors, we have
Hence, if two vectors  and
and  are given by
are given by  and
and 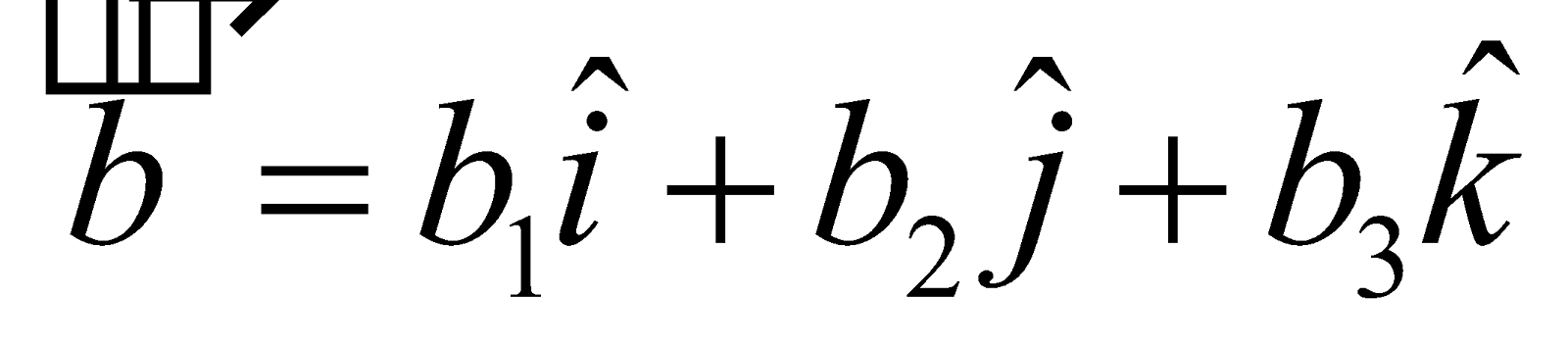 , we have
, we have .
.
PROPERTIES OF SCALAR PRODUCTS
(Commutative Law)
(Distributive Law)
- There is no associative law for the scalar product since
is not defined as
is scalar and the scalar product is an operation on two vectors.
- If the scalar product of a vector
with each of three non-coplanar vectors is zero then
must be the zero vector, because no non-zero vector can be perpendicular to three non-coplanar vectors.
In particular, if a vector is perpendicular to every vector then
is perpendicular to every vector then be a zero vector.
be a zero vector.
- Cancellation law does not hold necessarily.
If , then is not necessarily equal to
, then is not necessarily equal to since
since  is also true when
is also true when  is perpendicular to
is perpendicular to . Thus
. Thus  if
if
(i)  or (ii)
or (ii)  or (iii)
or (iii)  is perpendicular to
is perpendicular to .
.
- If
and
be parallel vectors, then
SOME USEFUL VECTOR IDENTITIES
[∵ Square of a vector = square of its modulus]
- Similarly
- If
APPLICATION OF SCALAR PRODUCT OF VECTORS
TO FIND ANGLE BETWEEN TWO VECTORS
If θ be the angle between two non-zero vectors,  and
and  then we have
then we have 
where  are the unit vectors in the directions of
are the unit vectors in the directions of  and
and  respectively.
respectively.
The angle between two non-zero vectors and is given by  .
.
Further, if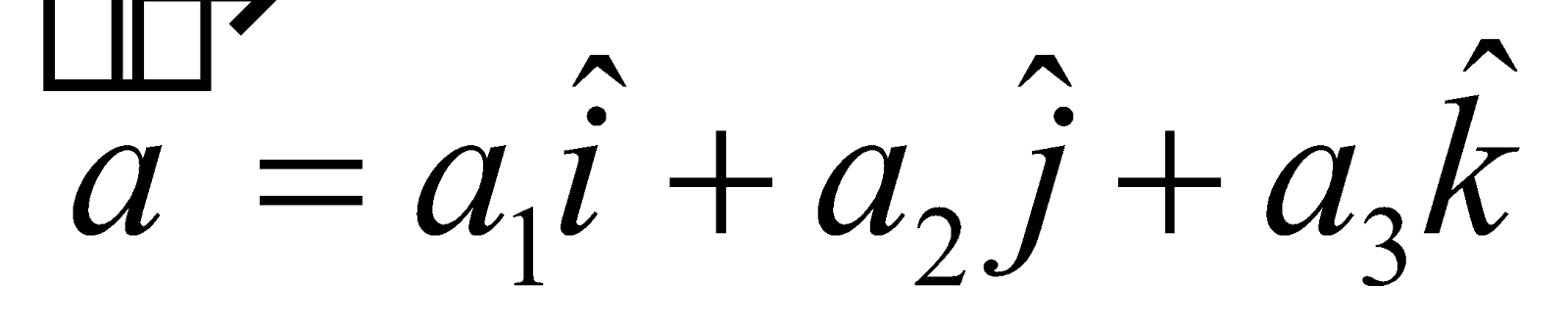 and
and  . Then the angle θ between
. Then the angle θ between  and
and is given by
is given by
TO FIND PROJECTION AND COMPONENT OF A VECTOR
We know that the scalar product of two vectors is the product of the magnitude of either vector and the projection of the other in that direction.
or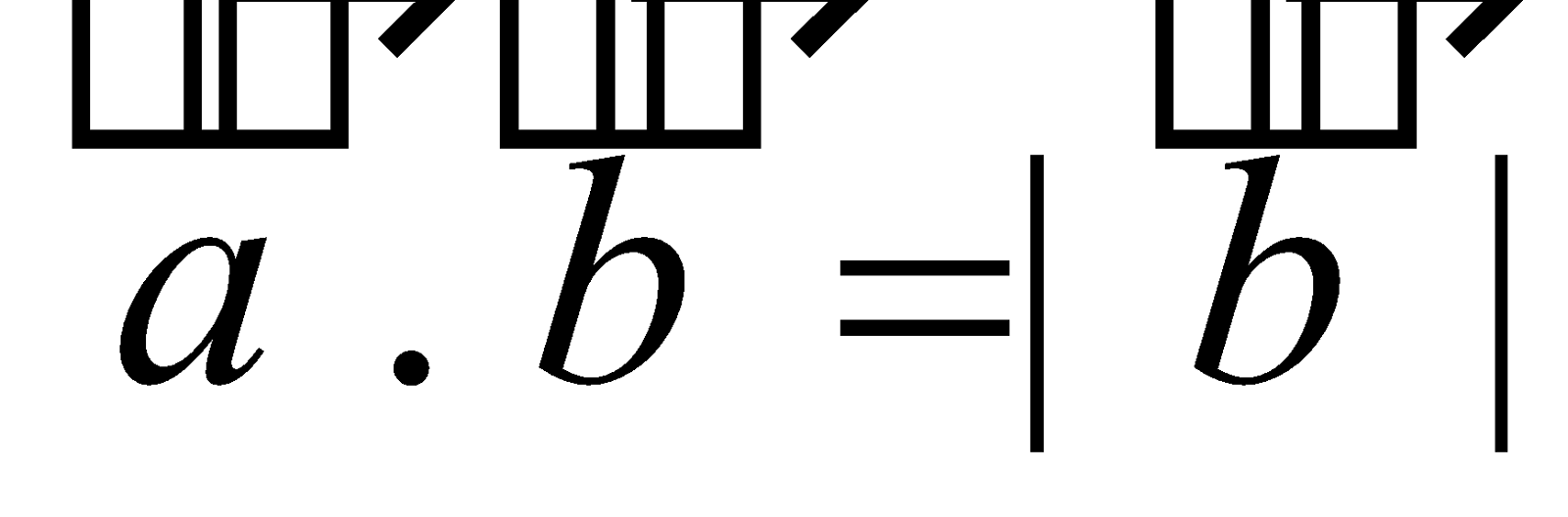 × projection of
× projection of  on
on .
.
It follows from the above that projection of on
on =
=
Projection of  on
on =
= 
Vector component of a vector on
on 
Vector component of a vector
= 
Similarly, the vector projection of  on
on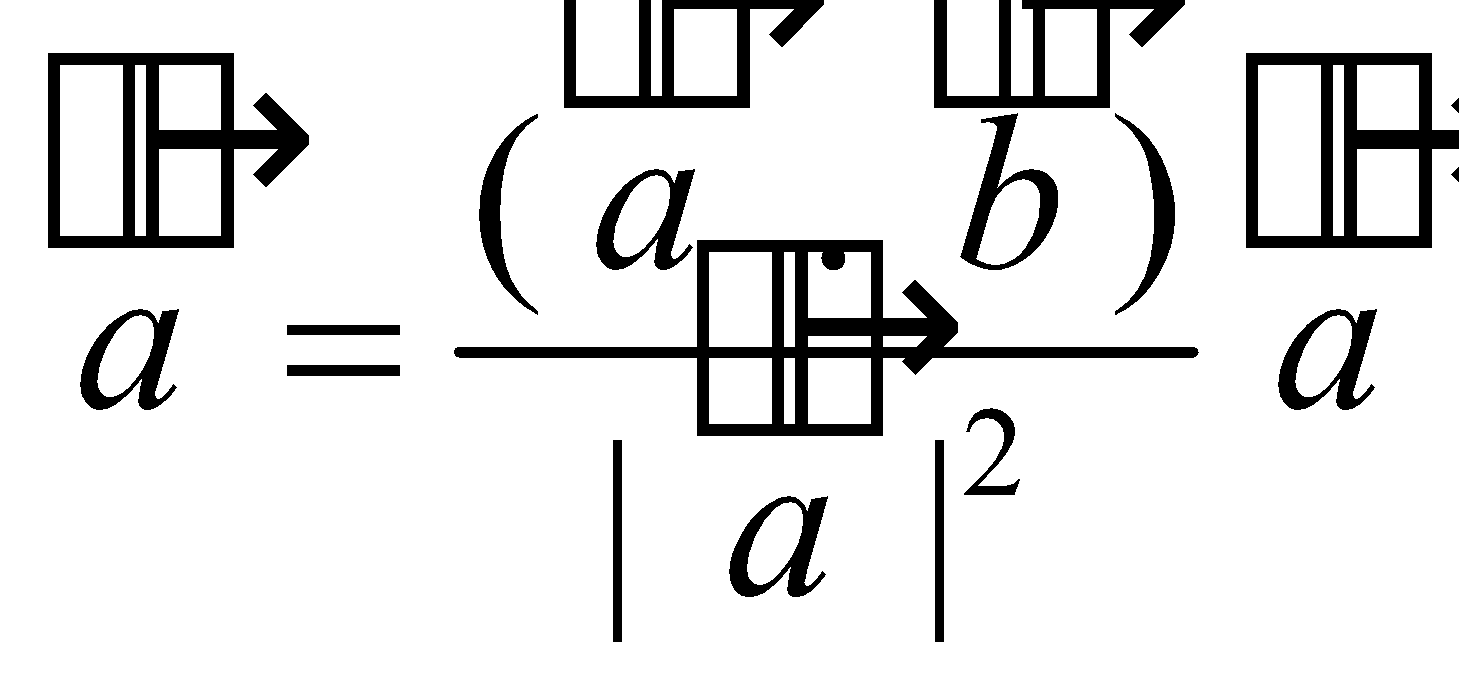 .
.
RESOLVED PARTS
Resolved parts of a vector 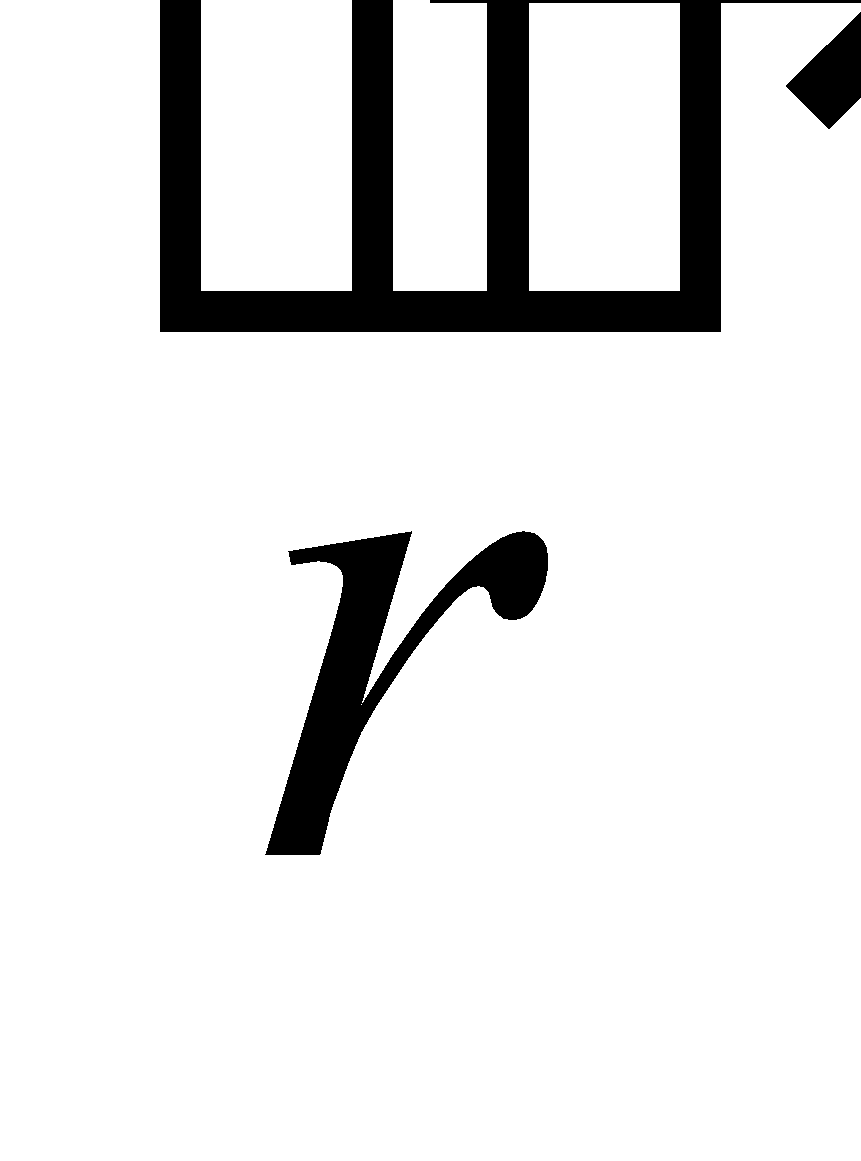 in the direction of a unit vector
in the direction of a unit vector  and in the direction perpendicular
and in the direction perpendicular to are respectively
to are respectively  and
and .
.
Clearly the scalar and vector components of a vector  in direction of coordinates axes are respectively
in direction of coordinates axes are respectively
Hence, 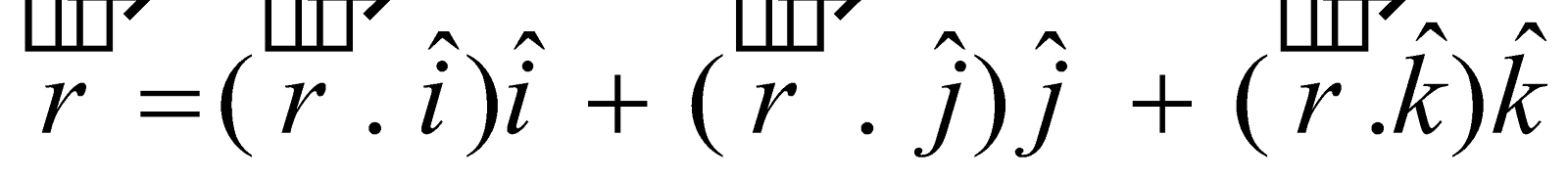 .
.
TO FIND WORK DONE BY A FORCE
Work done by a force causing a displacement .
= displacement × component of the force along the displacement
= 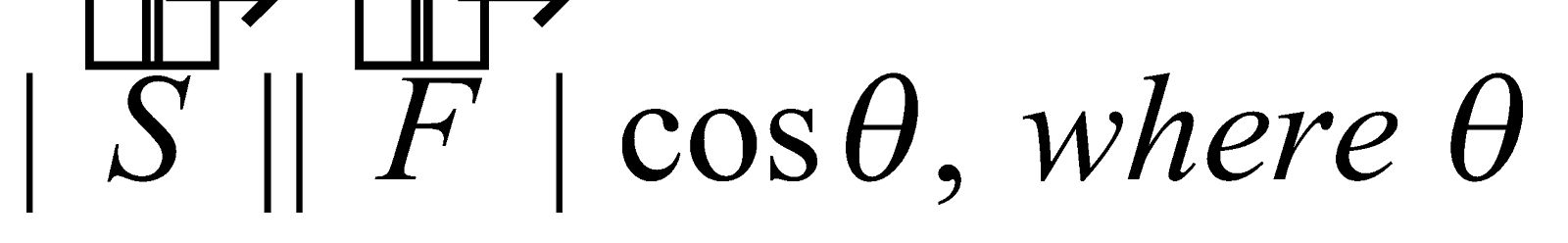 is the angle between
is the angle between  and
and 
=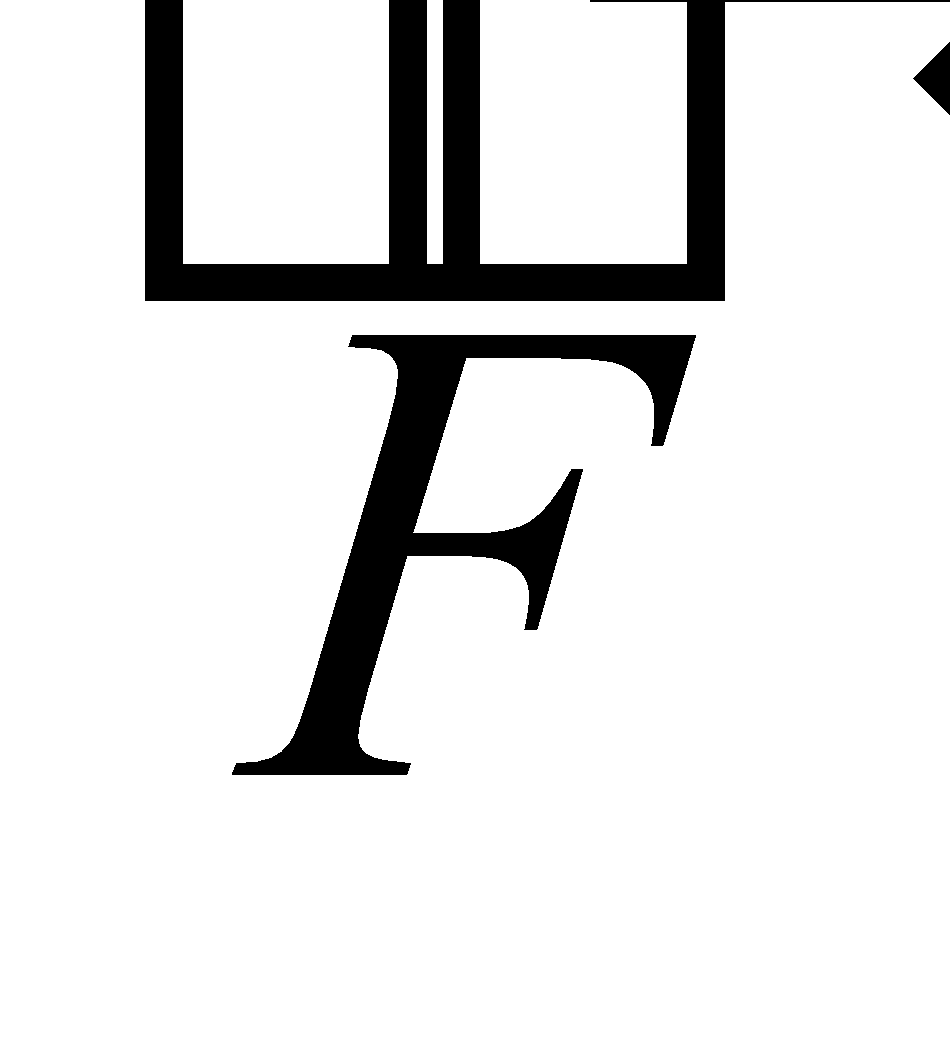 .
. = dot product of force and displacement
= dot product of force and displacement
Let a force displace a particle from a point A(x1, y1, z1) to B (x2, y2, z2). Then
displace a particle from a point A(x1, y1, z1) to B (x2, y2, z2). Then  .
.
= 
= 
Also, let 
Then work done by 
= 
= 
[Note : The work done is zero only  when is perpendicular to
when is perpendicular to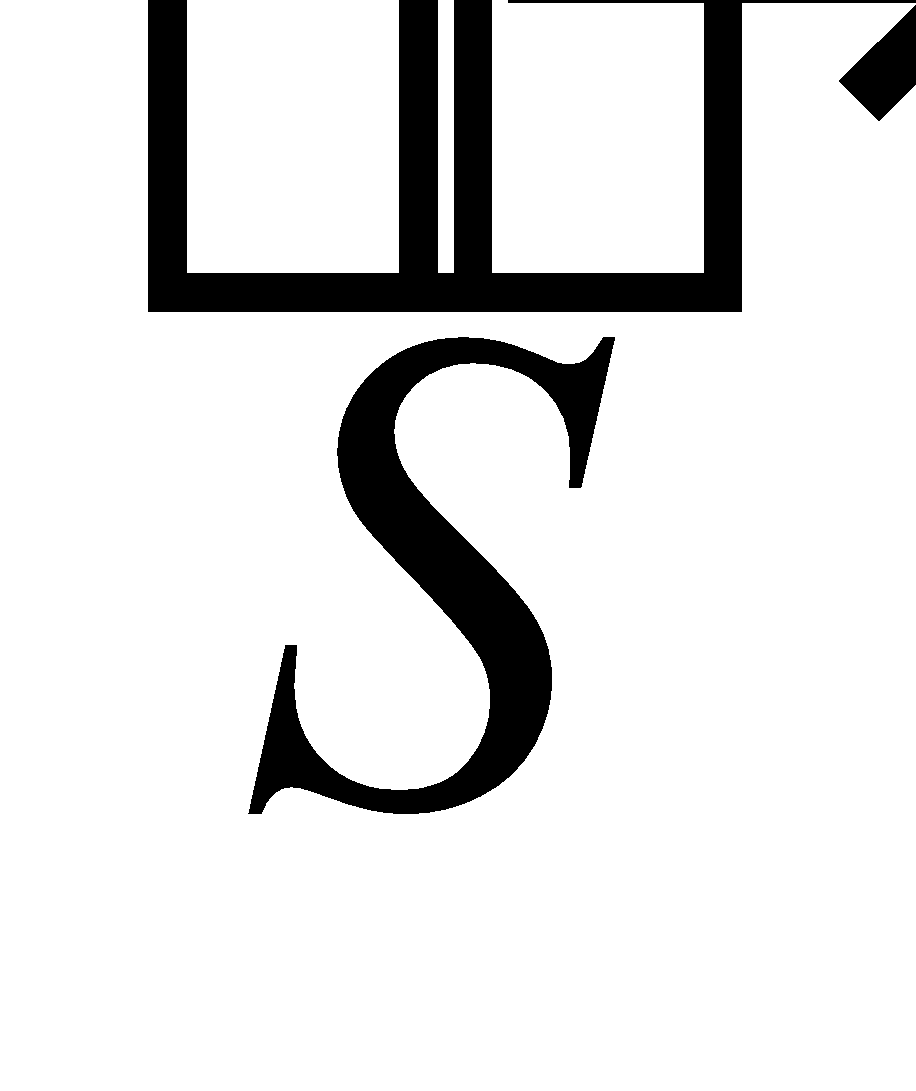 .]
.]
Suppose next that the particle is acted upon the forces  then during the displacement
then during the displacement 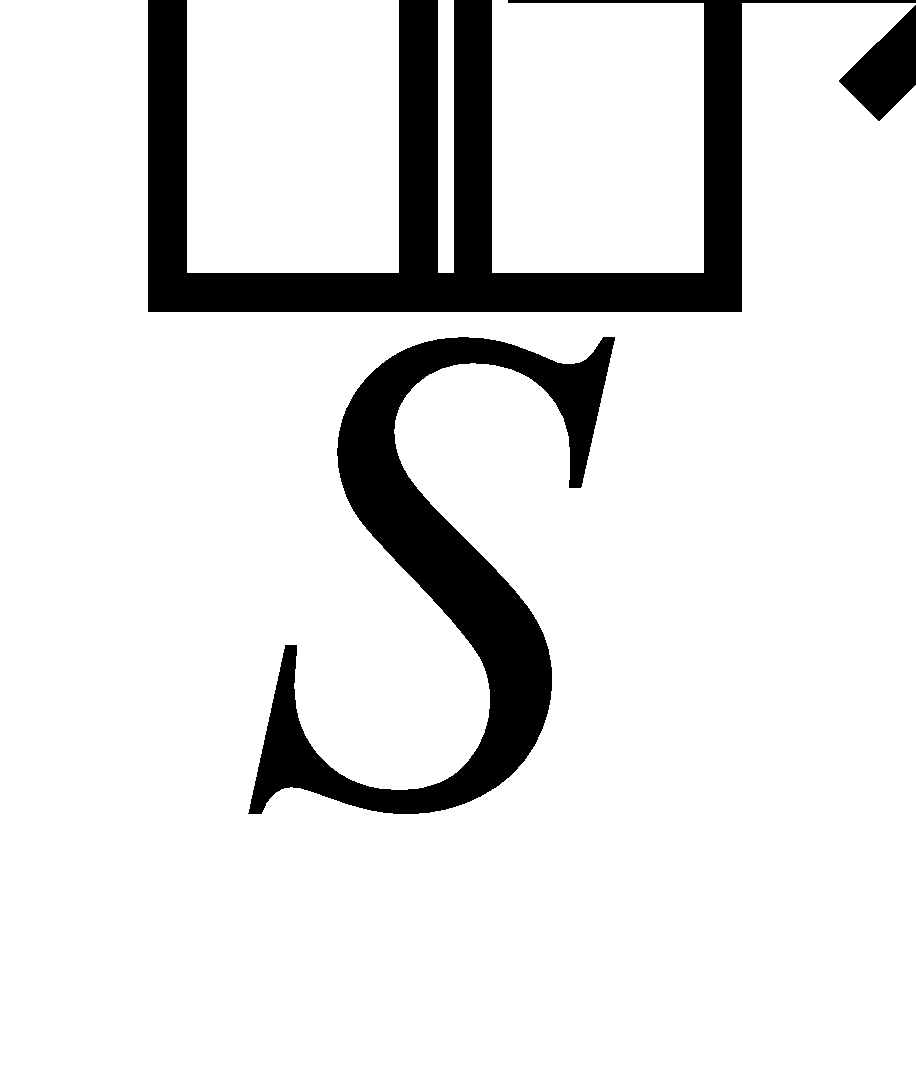 of the particle the separate forces do quantities of work
of the particle the separate forces do quantities of work  .
.
The total work done is  and is therefore the same as if the system of forces were replaced by its resultant
and is therefore the same as if the system of forces were replaced by its resultant .
.
VECTOR OR CROSS PRODUCT OF TWO VECTORS
The vector product of two vectors  and
and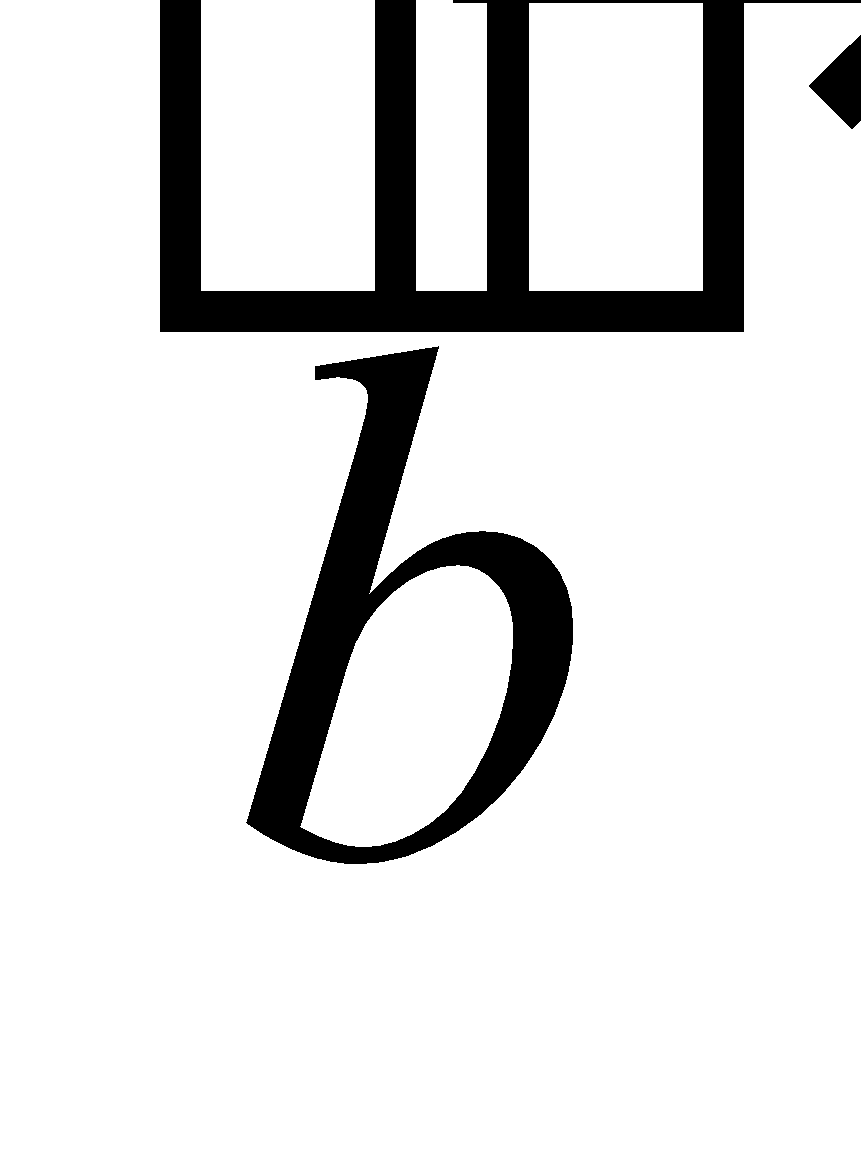 is a vector
is a vector whose magnitude is
whose magnitude is  , where
, where  and θ is the angle between the vectors
and θ is the angle between the vectors  and
and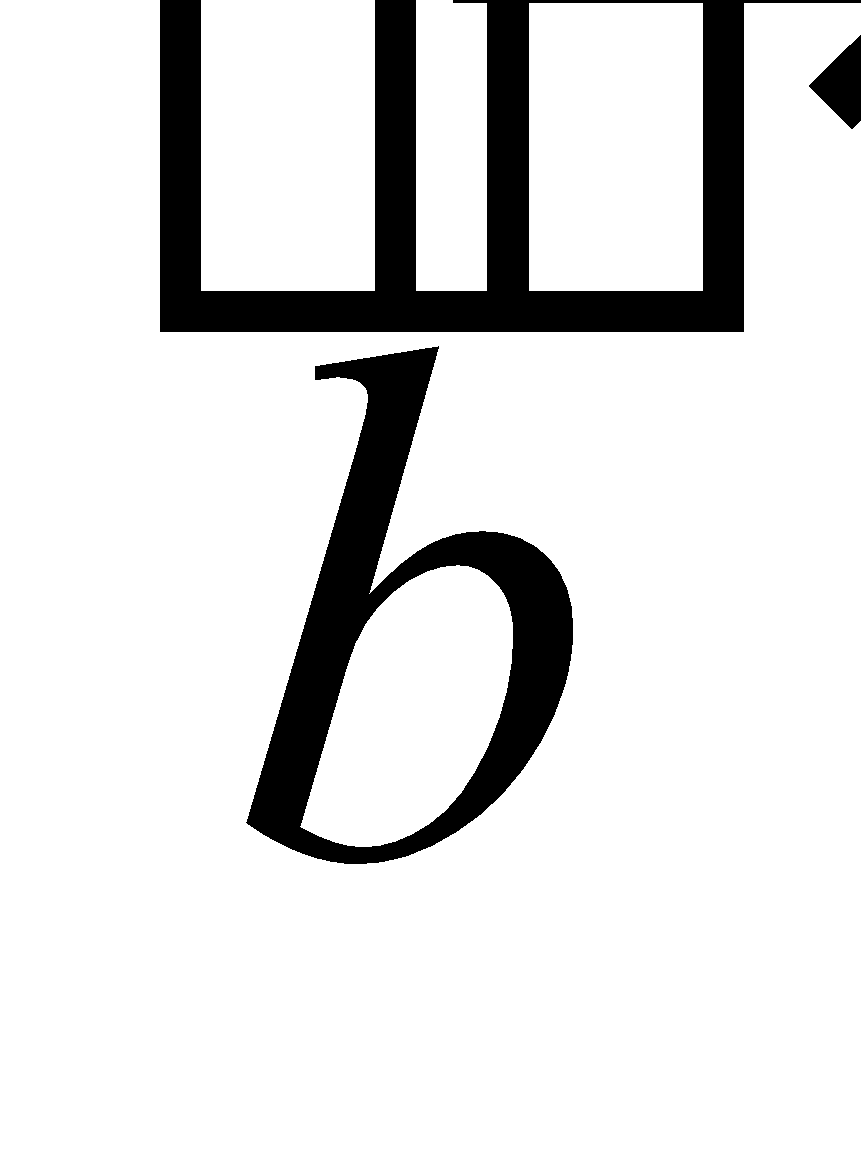 and the direction of
and the direction of is perpendicular to both the vectors
is perpendicular to both the vectors  , such that
, such that ,
,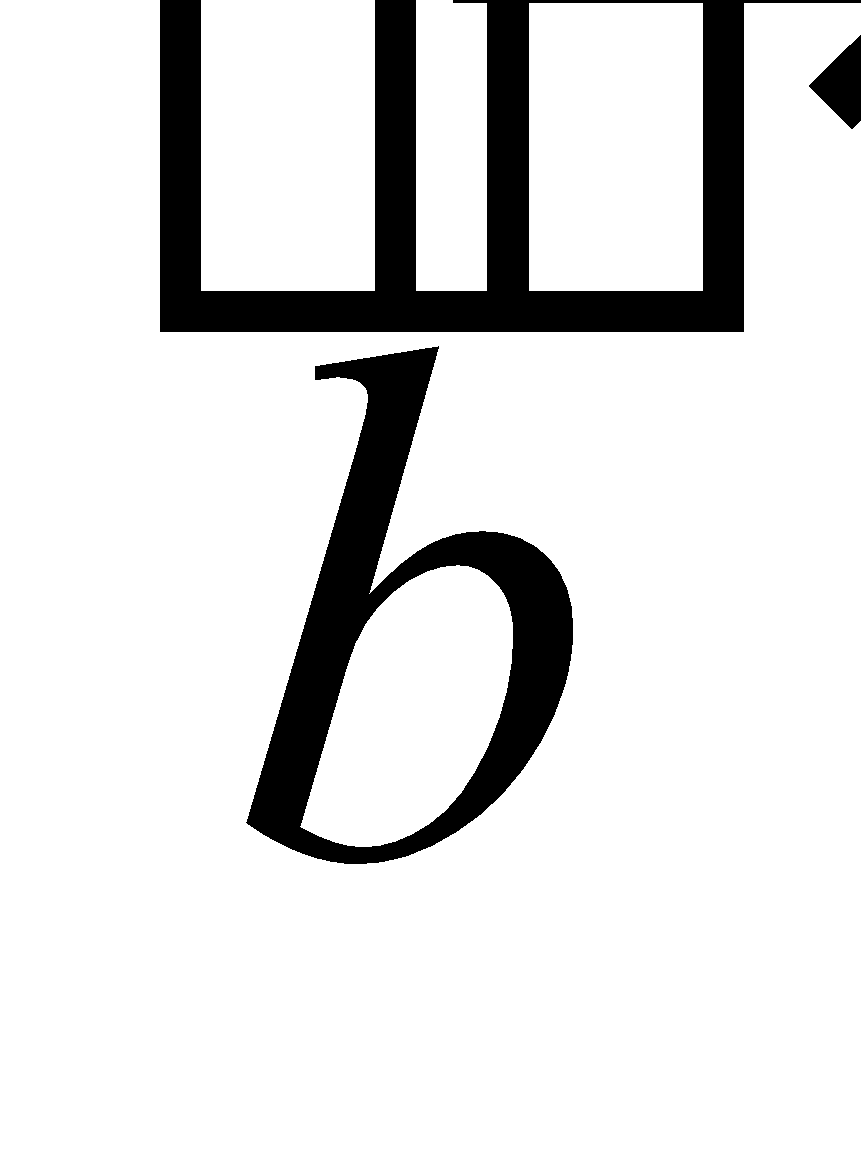 and
and form a right-handed screw.
form a right-handed screw.
The vector product of the vectors and
and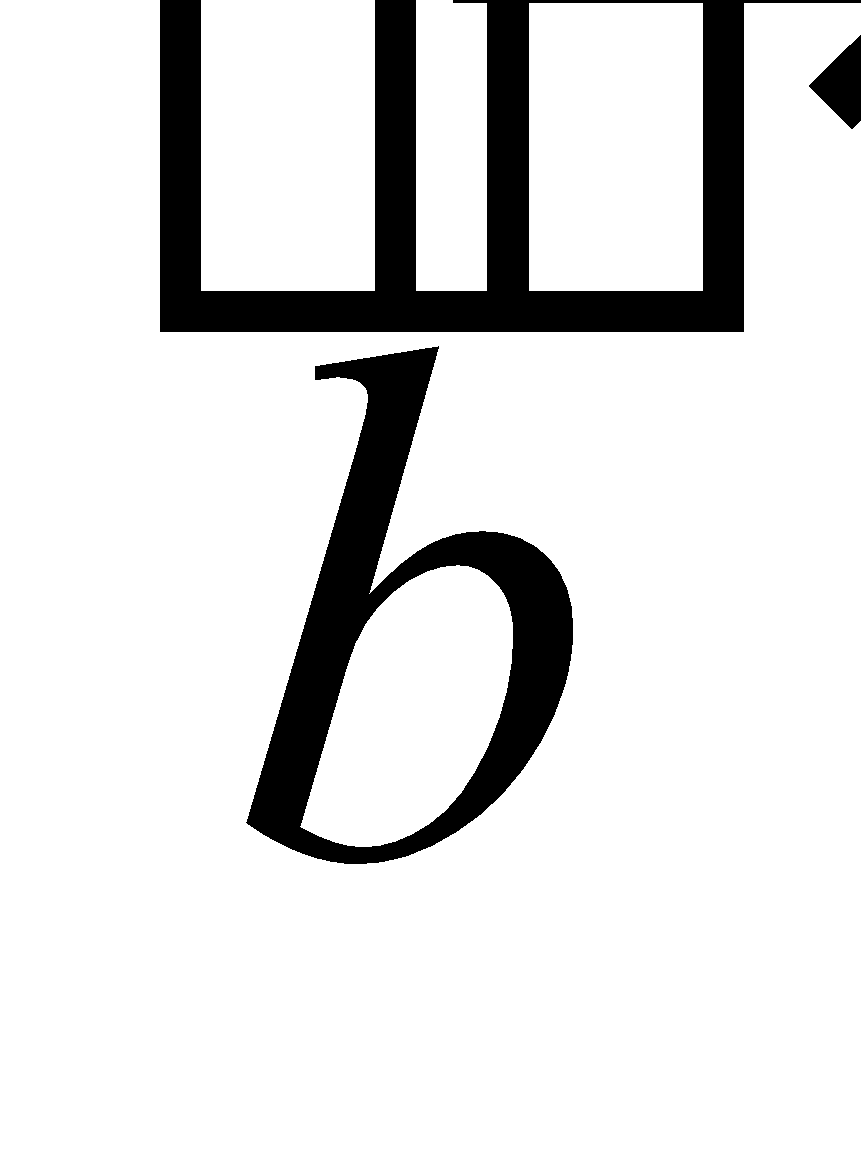 is denoted by
is denoted by and from the above definition, we get
and from the above definition, we get
or  .....(2)
.....(2)
where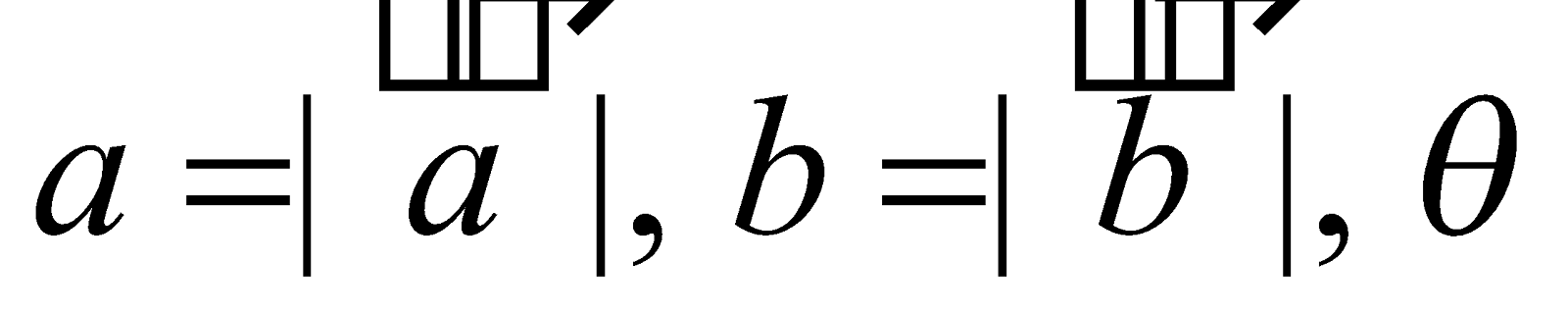 is the angle between the vectors
is the angle between the vectors  and
and , and is a unit vector perpendicular to both and such that from a right-handed triad of vectors.
, and is a unit vector perpendicular to both and such that from a right-handed triad of vectors.
IMPORTANT POINTS
- If
or if
is parallel to
, then
and
so.
- We define that the vector product of any vector with a null vector is a null vector i.e.
, if either
or
.
- The direction of
is regarded positive if the rotation from
to
appears to be anticlockwise.
is perpendicular to the plane which contains both
and
.
Thus, the unit vector perpendicular to both and
and or to the plane containing
or to the plane containing  is given by
is given by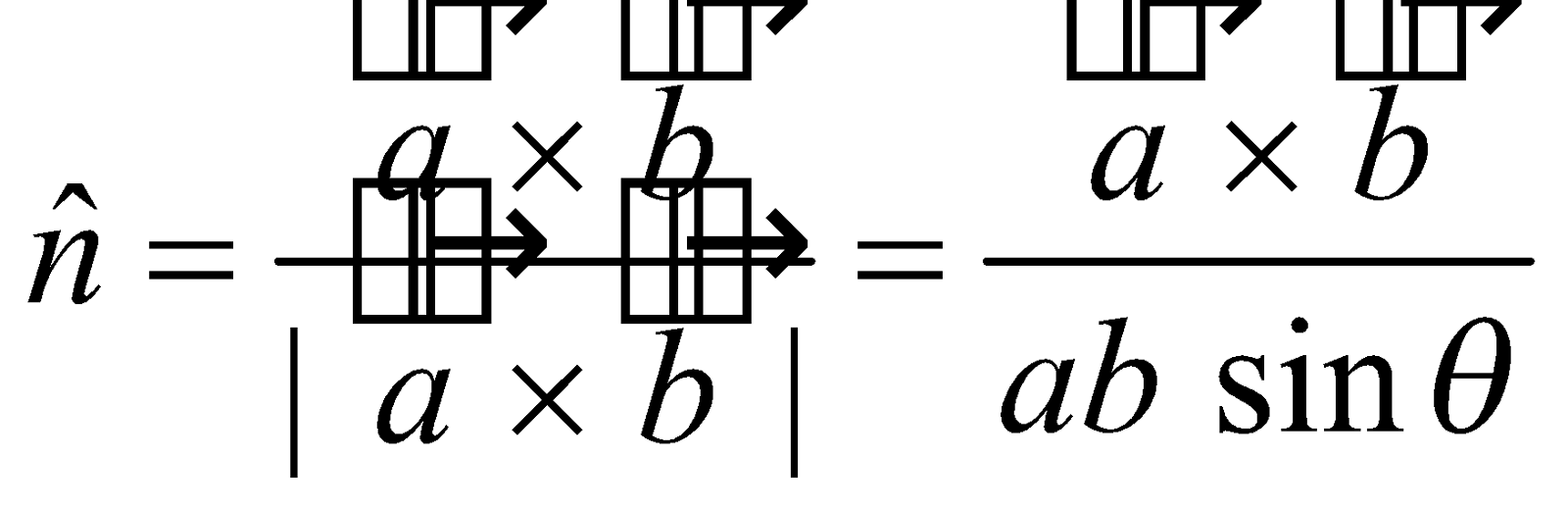 .
.
- Vector product of two parallel or collinear vectors is zero. If the vectors
and
are parallel or collinear, then θ = 0 or 180°, so in each case sin θ = 0. In particular
.
- If
, then
or
or
and
are parallel or collinear.
- Vector product of two perpendicular vectors
If , then
, then , i.e
, i.e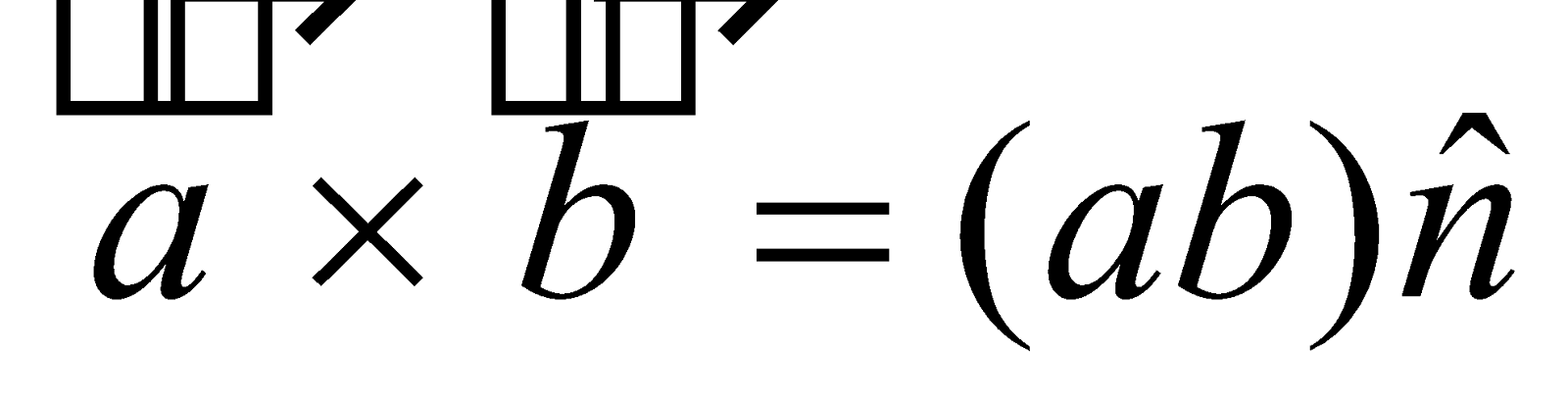 , or
, or  .
.
- Vector product of two unit vectors. If
and
, are unit vectors, then
GEOMETRICAL INTERPRETATION OF CROSS PRODUCT
- Let
and
be two non-parallel and non-null vectors. Let θ be the angle between OA and OB and
.
Then by definitionor
- Now complete the parallelogram OACB. Then area of parallelogram OACB = 2 (are Δ OAB)
= 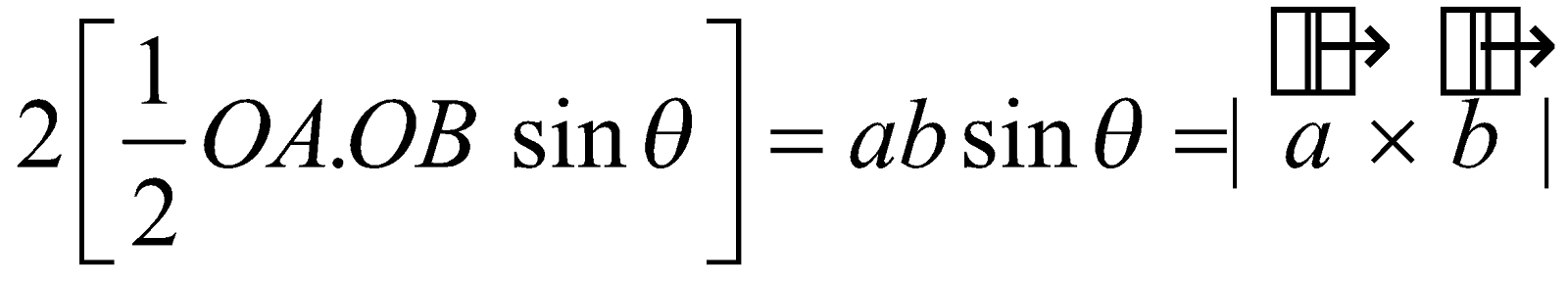 ......From (1)
......From (1)
- Hence
is a vector perpendicular to both
and
whose magnitude is equal to the area of the parallelogram whose adjacent sides are the vectors
and
.
Note : Vector area of Δ OAB = 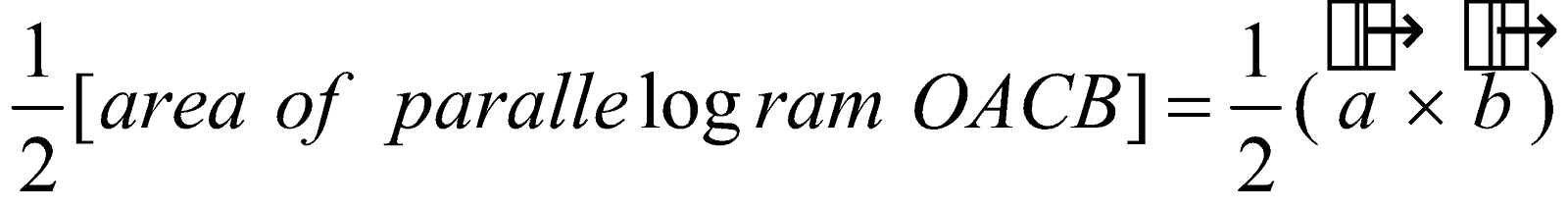
Area of Δ OAB = 
PROPERTIES OF VECTOR PRODUCT
- Vector product is not commutative : The two vector products
and
are equal in magnitude and opposite in direction.
Hence, we conclude that  .
.
Due to the result (i), vector product is said to be anti-commutative
- The vector product of a vector
with itself is a null vector, i.e.,
.
- Vector product is associative with respect to a scalar. Thus if
and
are any two vectors and m a scalar, then
- Distributive Law : For any three vectors
,
,
VECTOR PRODUCT IN TERMS OF COMPONENTS
Let  be the orthonormal triad of unit vectors then we have
be the orthonormal triad of unit vectors then we have 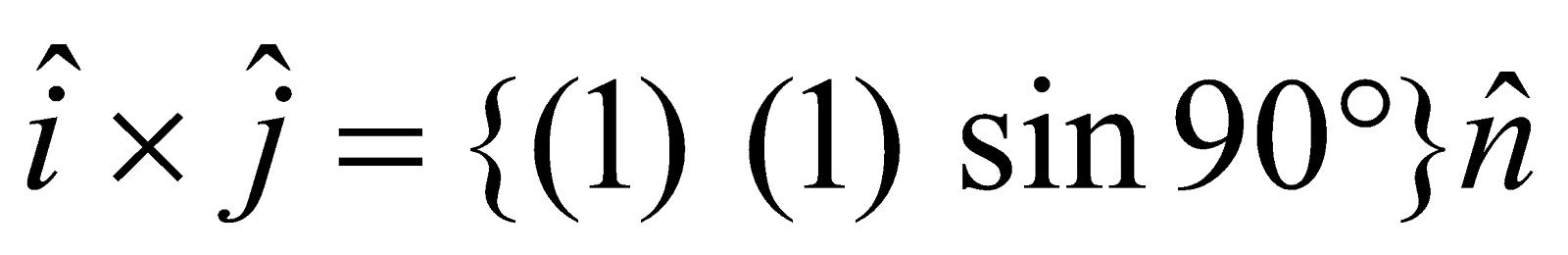 where
where is a unit vector perp. to both
is a unit vector perp. to both  and
and , i.e.
, i.e.  .
. 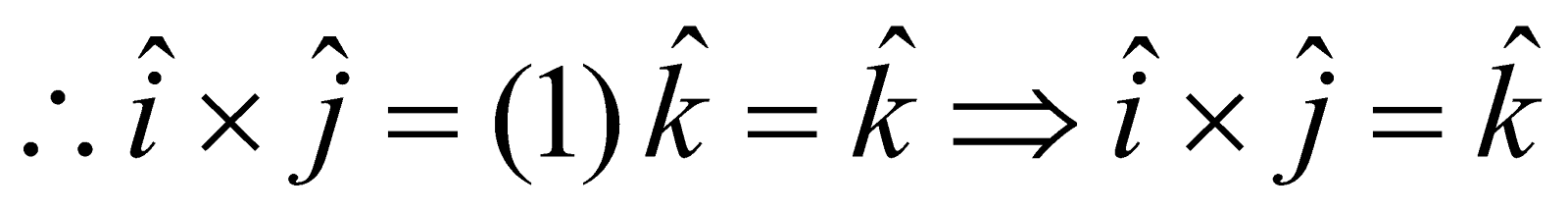 .
.
Similarly,  . Also,
. Also, 
Further,  as , so we have
as , so we have 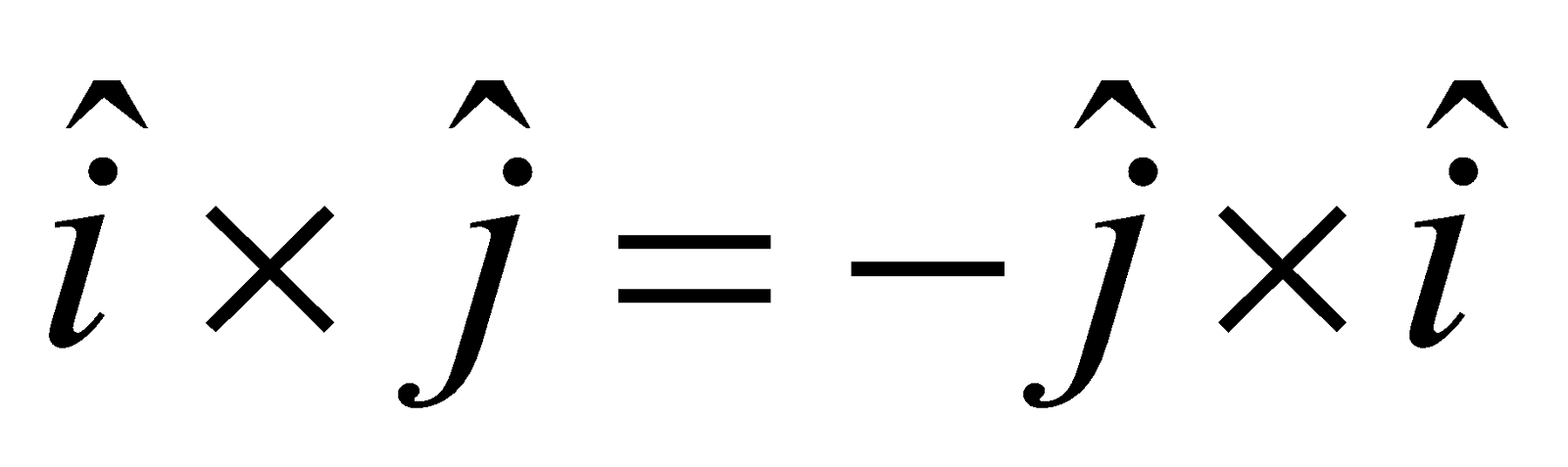 , etc.
, etc.
Hence 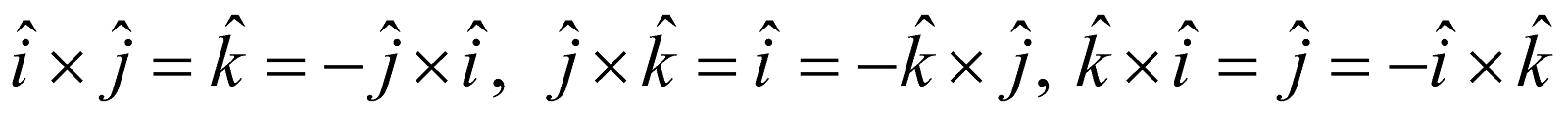
Let 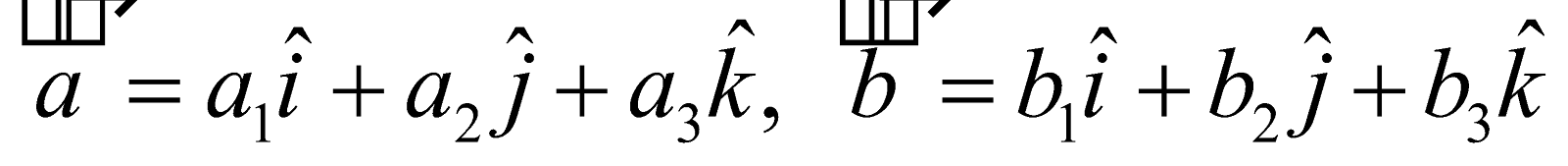
Then
Then
= 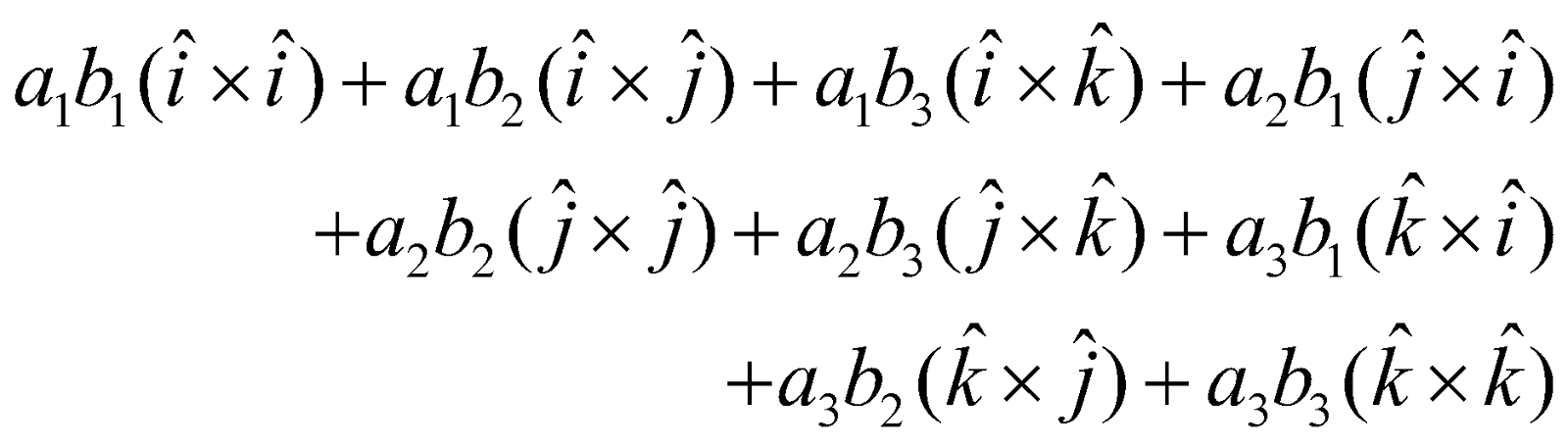
[Using results on cross products of orthonormal triads obtained above]
i.e. 
APPLICATION OF VECTOR PRODUCT
ANGLE BETWEEN TWO NON-ZERO, NON-PARALLEL VECTORS
[In terms of components]
Note : If 0 < sin θ < 1, then θ will have two value θ1 and θ2 such that 0 < θ1< 90° and 90° < θ2 < 180°. In this case angle between two vectors cannot be determined by the above formula. Hence, angle between two vectors should be evaluated using dot product.
CONDITION THAT TWO VECTORS MAY BE PARALLEL
If two vectors and
and  are parallel, then
are parallel, then  , i.e.,
, i.e., in both cases.
in both cases.
Thus two vectors are parallel if their corresponding components are proportional.
are parallel if their corresponding components are proportional.
TO FIND AREA OF A TRIANGLE AND PARALLELOGRAM
- The vector area of a triangle ABC is equal to
.
- The vector area of a triangle ABC with vertices having p.v.s
respectively is
.
- The points whose p.v.'s are
are collinear, if and only if
represents the vector area of the parallelogram OACB whose adjacent sides are
and
so that
form a vector triad in a right-handed system.
- Vector area of a quadrilateral ABCD is given by
.
TO FIND VECTOR MOMENT OF A FORCE ABOUT A POINT
The vector moment or torque  of a force
of a force about the point O is the vector whose magnitude is equal to the product of
about the point O is the vector whose magnitude is equal to the product of and the perpendicular distance of the point O from the line of action of
and the perpendicular distance of the point O from the line of action of  .
.
i.e., 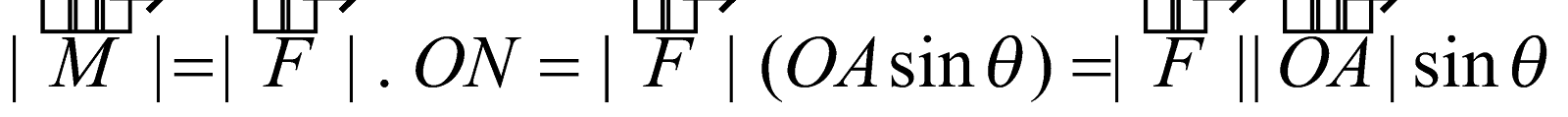
where is the position vector of A referred to O.
is the position vector of A referred to O.
The moment of a force about O is independent of the choice of point A on the line of action of
about O is independent of the choice of point A on the line of action of . If several forces are acting through the same point A, then the vector sum of the moments of the separate forces about a point O is equal to the moment of their resultant force about O.
. If several forces are acting through the same point A, then the vector sum of the moments of the separate forces about a point O is equal to the moment of their resultant force about O.
TO FIND THE MOMENT OF A FORCE ABOUT A LINE
Let  be a force acting at a point A, O be any point on the given line L and be the unit vector along the line, then moment of
be a force acting at a point A, O be any point on the given line L and be the unit vector along the line, then moment of about the line L is a scalar given by
about the line L is a scalar given by .
.
TO FIND THE MOMENT OF A COUPLE
Two equal and unlike parallel forces whose lines of action are different are said to constitute a couple. Let P and Q be any two points on the lines of action of the forces – and
and respectively.
respectively.
The moment of the couple =  .
.
TRIPLE PRODUCTS OF VECTORS
SCALAR TRIPLE PRODUCTS
For any three given vectors, the scalar product of one of the vectors and the cross product of the remaining two, is called a scalar triple product.
Thus, 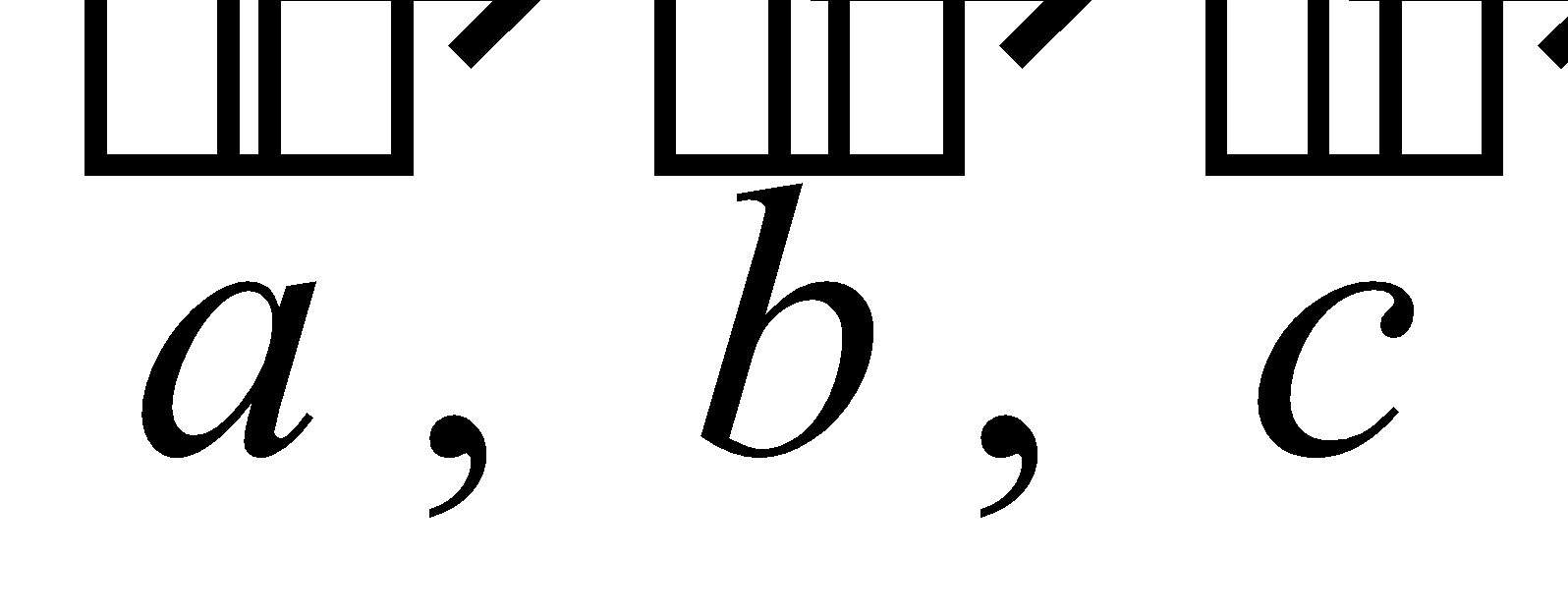 If are three vectors, then
If are three vectors, then  is called scalar triple product and is denoted by
is called scalar triple product and is denoted by  .
.
GEOMETRICAL INTERPRETATION OF SCALAR TRIPLE PRODUCT
The scalar triple product 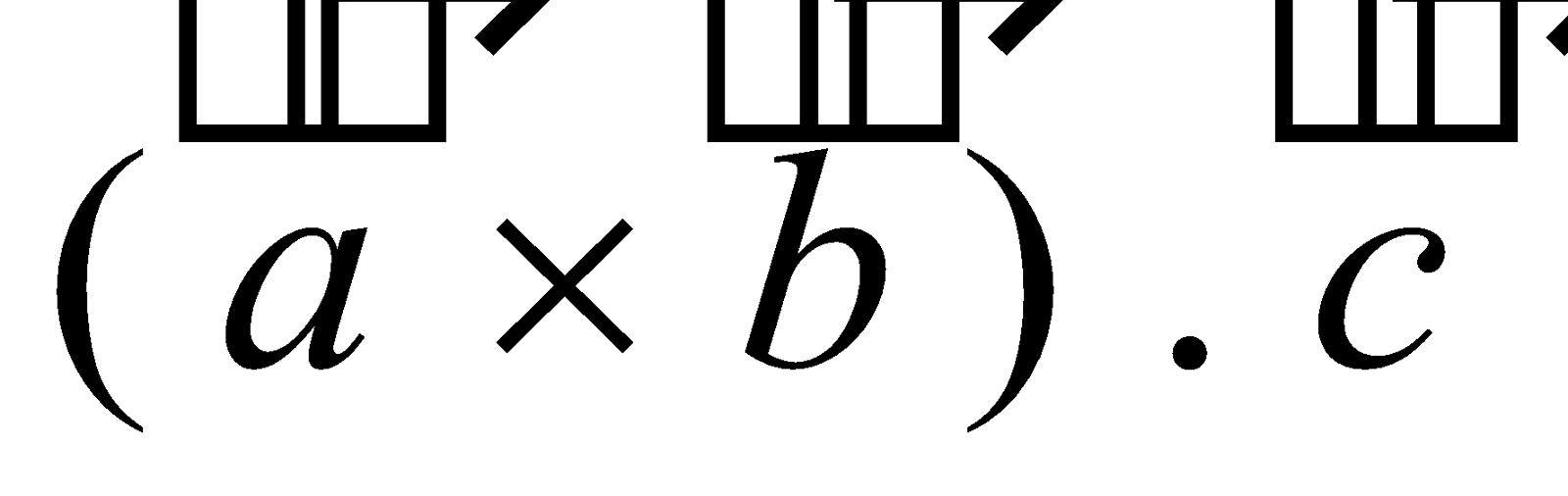 represents the volume of a parallelepiped whose coterminous edges are represented by
represents the volume of a parallelepiped whose coterminous edges are represented by  which form a right handed system of vectors.
which form a right handed system of vectors.
Note : The scalar triple product is positive or negative according as form a right handed or a left handed system respectively.
is positive or negative according as form a right handed or a left handed system respectively.
EXPRESSION OF THE SCALAR TRIPLE PRODUCT IN TERMS OF COMPONENTS
IN TERMS OF COMPONENTS
Let , 
then
= 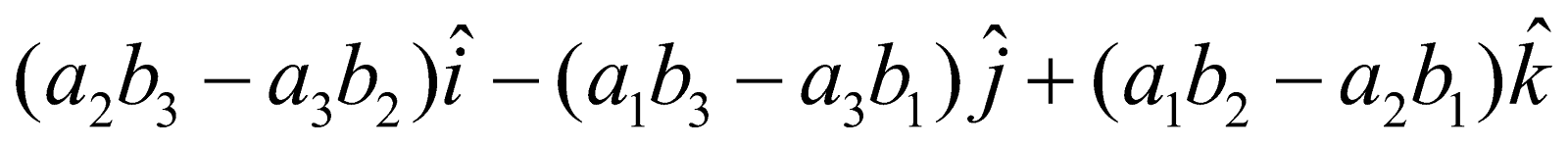
= 
= 
or 
PROPERTIES OF SCALAR TRIPLE PRODUCTS
- The scalar triple product is independent of the positions of dot and cross i.e.,
.
- The scalar triple product of three vectors is unaltered so long as the cyclic order of the vectors remains unchanged, i.e.
,
or
- The scalar triple product changes in sign but not in magnitude, when the cyclic order is changed.
etc.
- The scalar triple product vanishes if any two of its vectors are equal.
i.e. 
- The scalar triple product vanishes if any two of its vectors are parallel or collinear.
- For any scalar x,
Also, 
- For any vector
- Three non-zero vectors are coplanar if and only if
.
- Four points A, B, C, D with position vectors
respectively are coplanar if and only if
, i.e., if and only if
.
- Volume of parallelopiped with three coterminous edges
- Volume of prism on a triangular base with three coterminous edges .
- Volume of a tetrahedron with three coterminous edges
TO EXPRESS IN TERMS OF NON-COPLANAR VECTORS
IN TERMS OF NON-COPLANAR VECTORS
Let 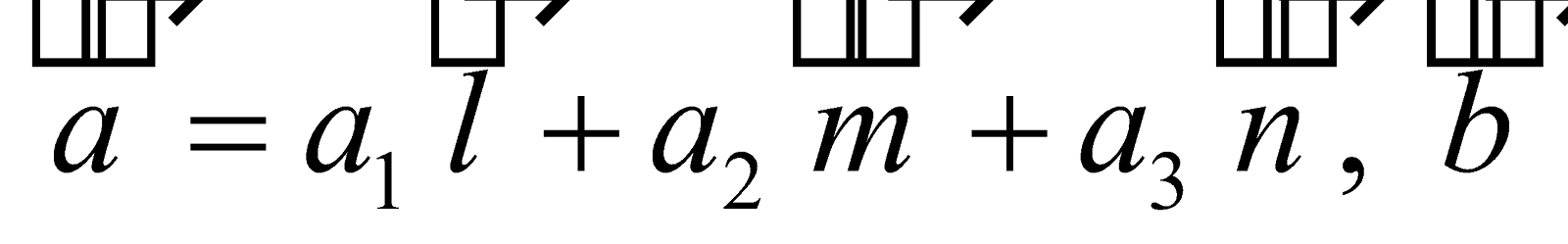
Then , 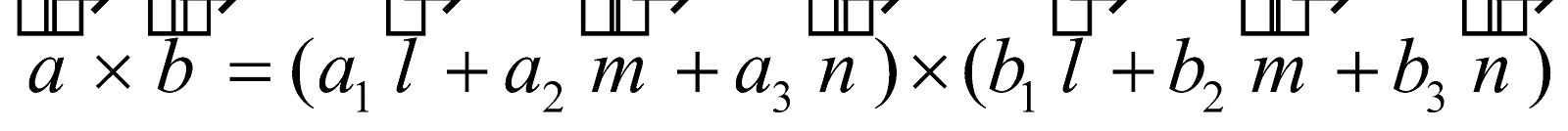
= 
VECTOR TRIPLE PRODUCT
If  be any three vectors, then
be any three vectors, then  and
and  are known as vector triple product
are known as vector triple product
THEOREM : For any three vectors, 
IMPORTANT PROPERTIES
is a vector in the plane of vectors
and
.
, that is the cross product of vectors is not associative.
, if and only if
, if and only if
if
if and only if
is parallel to
. [
be non-zero vectors]
PRODUCTS OF FOUR VECTORS
SCALAR PRODUCT OF FOUR VECTORS
Let  be four vectors. Then their scalar product is defined by
be four vectors. Then their scalar product is defined by .
.
THEOREM : For any four vectors 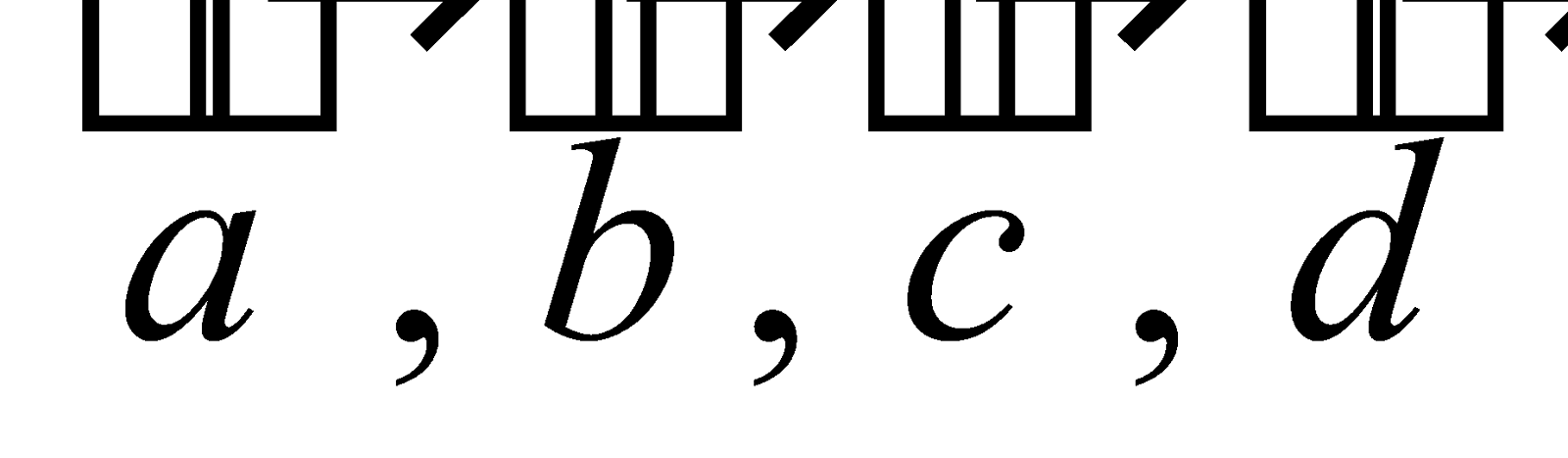
= 
VECTOR PRODUCT OF FOUR VECTORS
Let  be four vectors. Then the vector
be four vectors. Then the vector  is defined as the vector product of the four vectors.
is defined as the vector product of the four vectors.
THEOREM : For any four vectors 
EXPRESSING A VECTOR IN TERMS OF THREE NON-COPLANAR VECTORS
IN TERMS OF THREE NON-COPLANAR VECTORS 
Let  be non-coplanar vectors, then any vector
be non-coplanar vectors, then any vector  in space can be expressed as
in space can be expressed as
RECIPROCAL SYSTEM OF VECTORS
Let 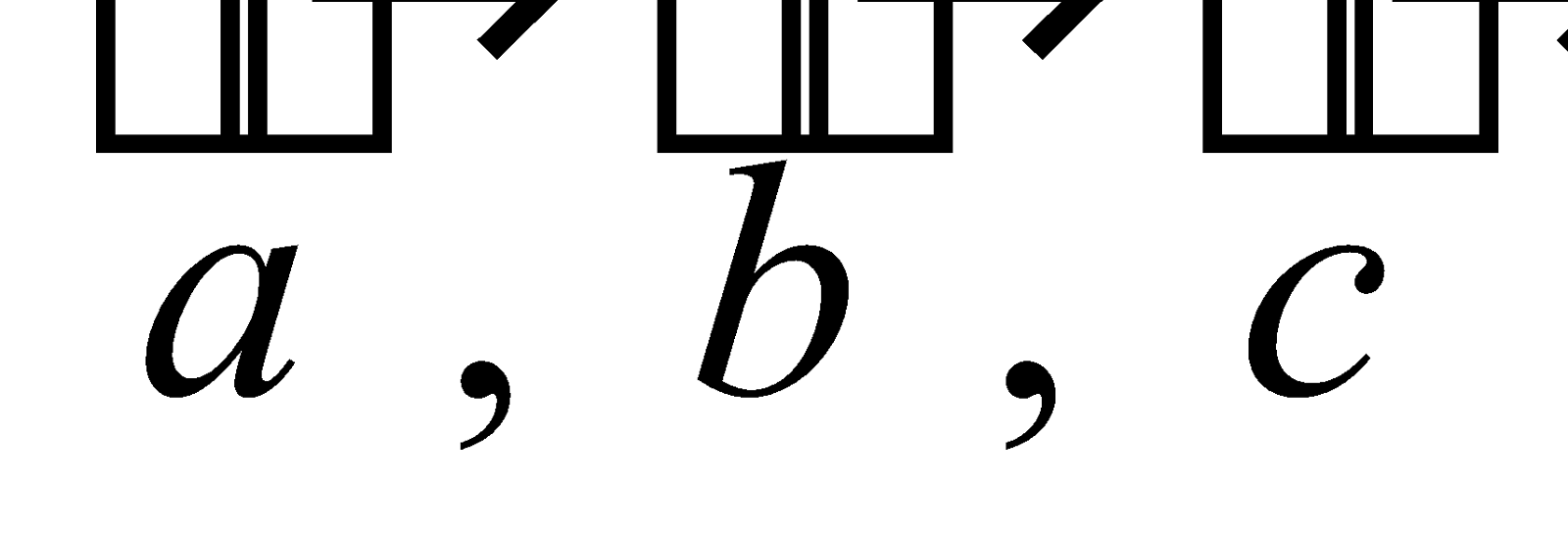 form a system of non-coplanar vectors. Then the three vectors
form a system of non-coplanar vectors. Then the three vectors defined by
defined by
are called reciprocal system of vectors to the system of vectors  .
.
PROPERTIES OF RECIPROCAL SYSTEM
.
.
Thus,  is reciprocal to the system
is reciprocal to the system  .
.
- The orthonormal vector triad
form a self-reciprocal system.
- If
be a system of non coplanar vectors and
be the reciprocal system of vectors, then any vector
can be expressed as







