TRIGONOMETRIC EQUATIONS AND INEQUATIONS
TRIGONOMETRIC EQUATIONS
The equations containing trigonometric functions of angles are called trigonometric equations, which hold for some values (and not for all values) of the angles involved. The set of values which, when substituted for the variable angle or angles, satisfy the given equation are called the SOLUTIONS (or ROOTS) of the equation.
A trigonometric equation may have infinite number of solutions which are classified as
- Principal Solution : The solutions of a trigonometric equation in the variable ‘x’ for which are called principal solutions.
For example
The principal solutions of the equation  are
are 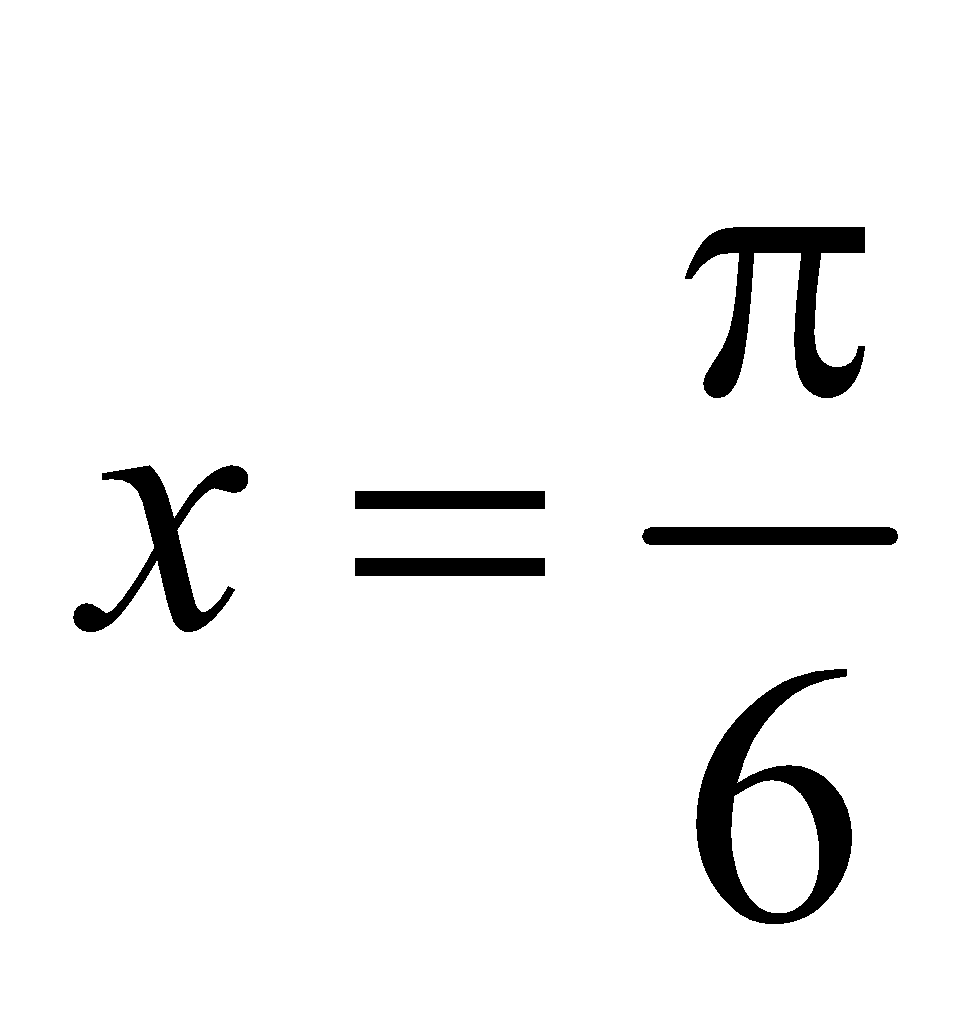 and
and 
The principal solutions of the equation are x =
are x = 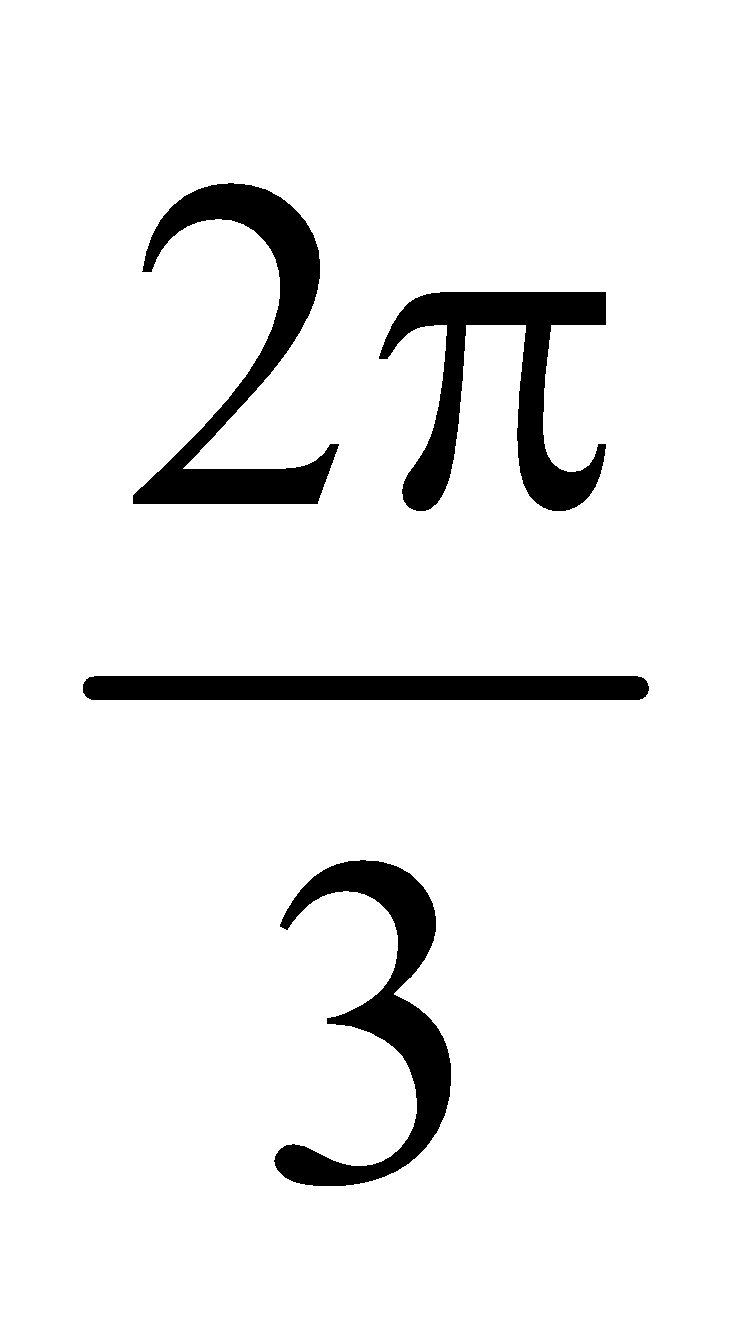 and
and 
- General Solution : The solution consisting of all possible solutions of a trigonometric equation generalised by means of periodicity of the trigonometric functions is called the general solution.
GENERAL SOLUTION OF ELEMENTARY TRIGONOMETRIC EQUATIONS
If 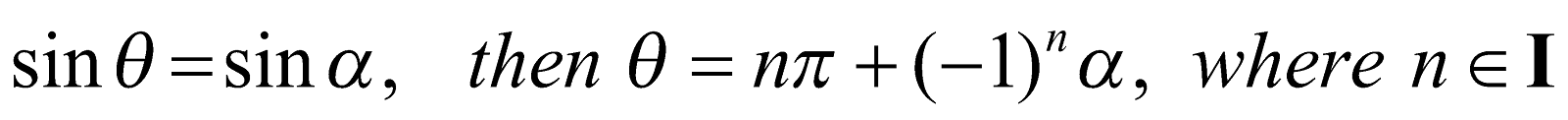
α is the principal value in each case.
SOLUTION OF BASIC EQUATIONS
DIFFERENT METHODS OF SOLVING TRIGONOMETRIC EQUATIONS
SOLUTION OF EQUATIONS BY FACTORING
Example :
Solve : 2 cos x cos 2x = cos x.
Solution :
The given equation is equivalent to the equation
cos x (2 cos 2x –1) = 0.
This equation is equivalent to the collection of equations
Answer :
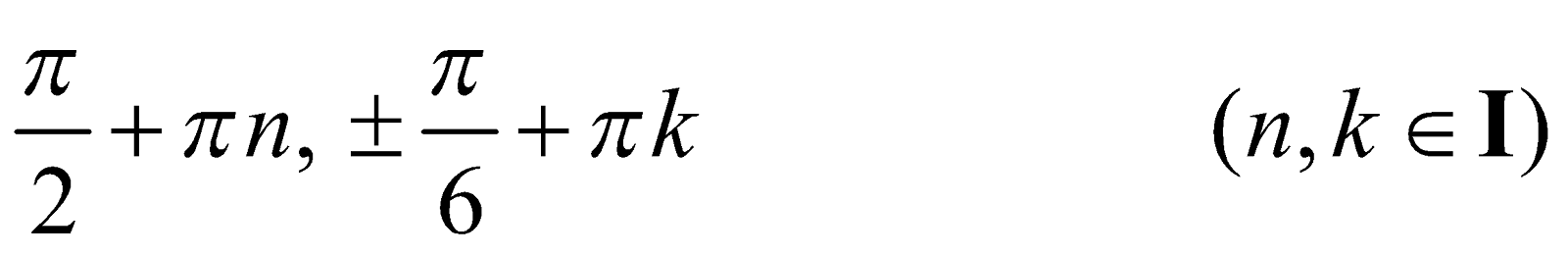
SOLUTION OF EQUATIONS REDUCIBLE TO QUADRATIC EQUATIONS
Example :
Solve the equation 3 cos2x – 10 cos x + 3 = 0.
Solution :
Assume cos x = y. The given equation assumes the form 3y2 – 10 y +3 = 0.
Solving it, we find that 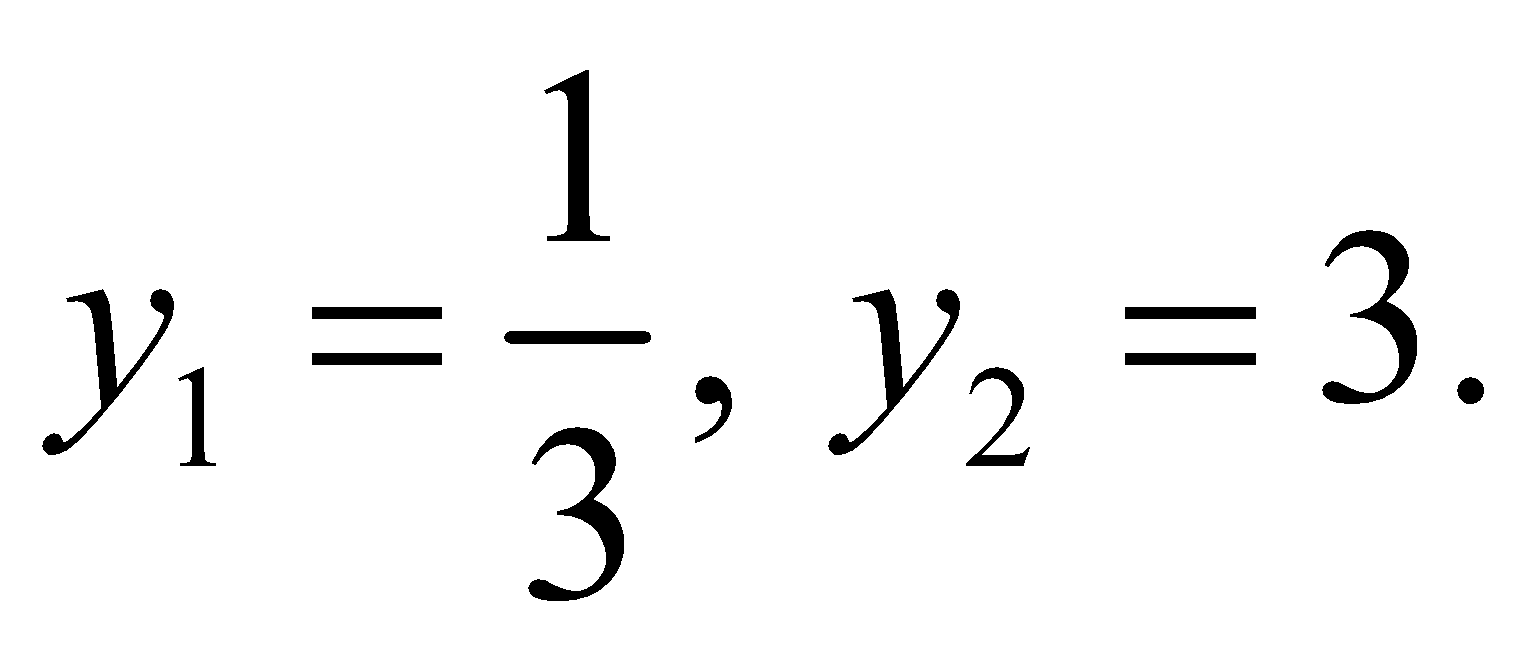
The value y2 = 3 does not satisfy the condition since | cos x | ≤ 1.
Consequently, 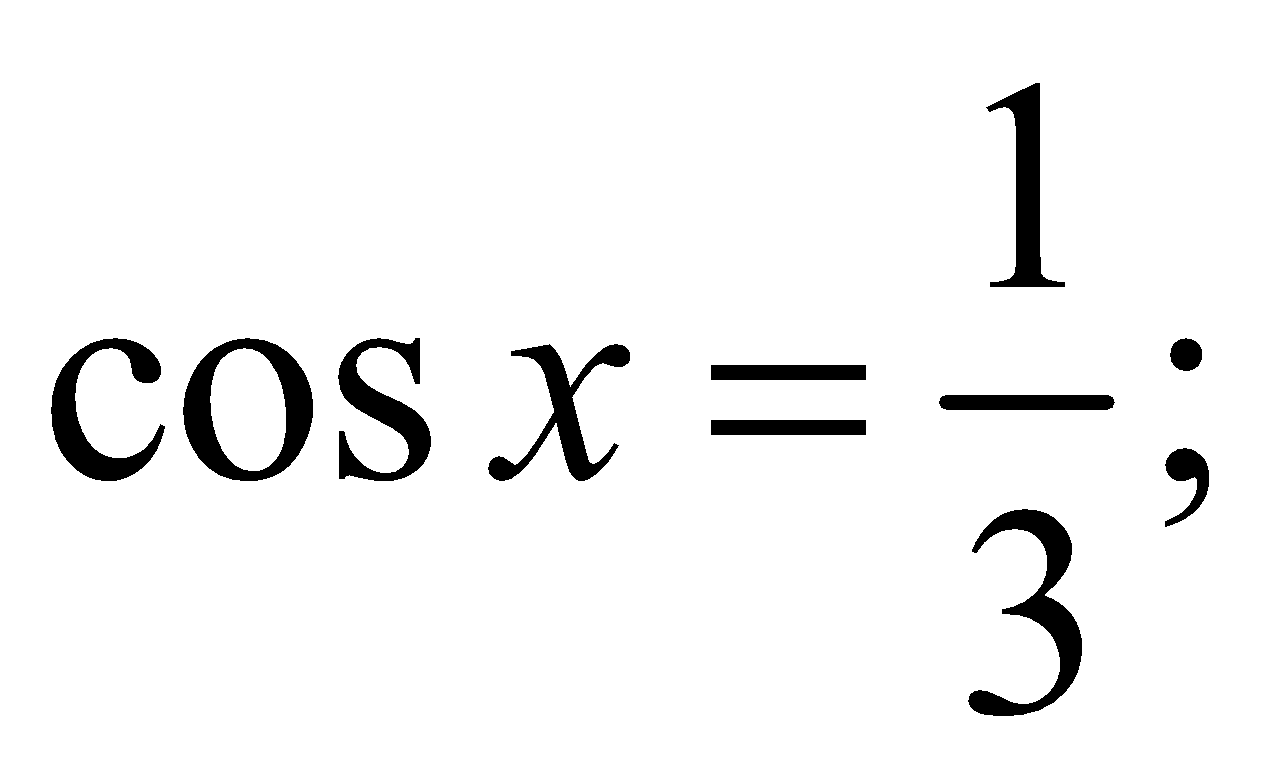
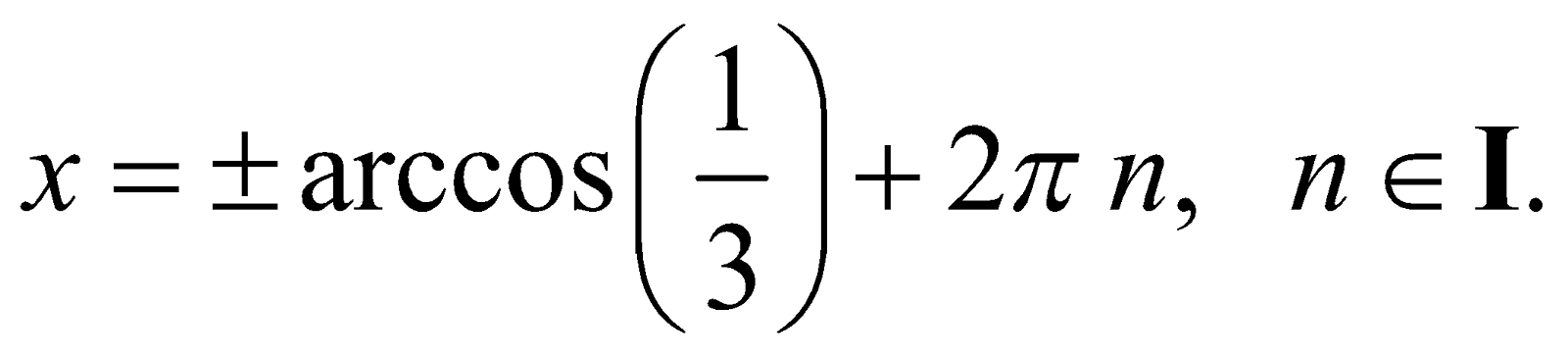
Answer :
SOLUTION OF HOMOGENEOUS EQUATIONS AND EQUATIONS REDUCIBLE TO HOMOGENEOUS FORMS
Equations of the form
a0 sinnx +a1 sinn–1 x cos x + a2 sinn–2 x cos2 x +.....+an–1 sin x cosn–1 x + an cos n x = 0.
(Where a0, a1, ......, an are real numbers), are said to be homogeneous with respect to sin x and cos x. Such an equation is solved by dividing the equation by cosn x.
Example 1 : Solve the equation cos 3 x + sin 3 x = 0
Solution : sin3x = – cos 3x.
Since the values of x for which cos3x is equal to zero cannot serve as roots for the given equation, we divide both sides of the initial equation by cos3x and obtain an equation, equivalent to the initial equation
Hence, 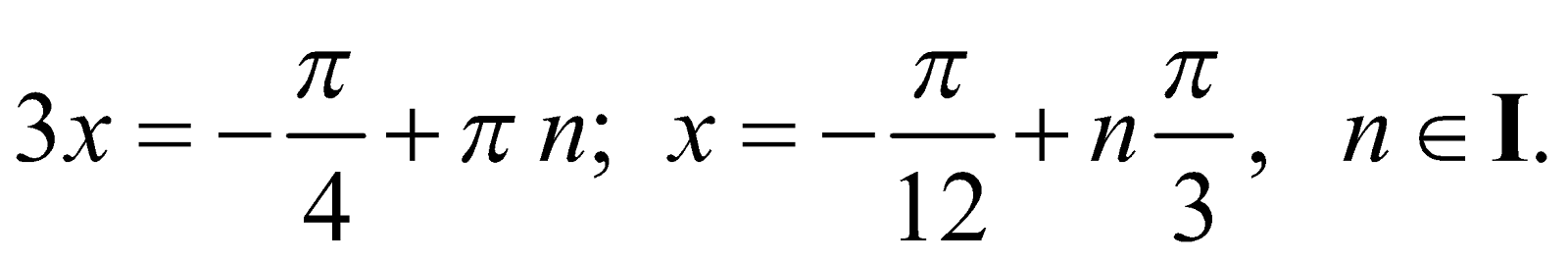
Answer : 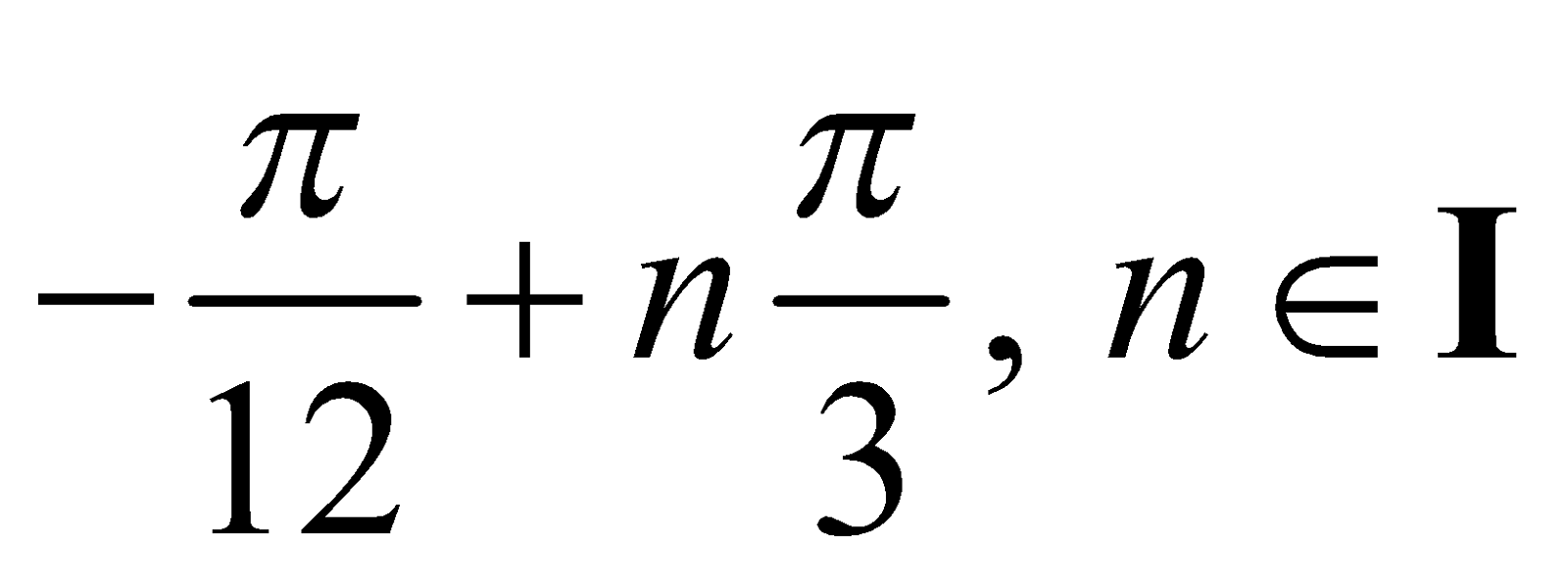
Example 2 :
Solve : 6 sin2 x – sin x cos x – cos2 x = 3
Solution :
6sin2 x – sin x cos x – cos2 x – 3 (sin2 x + cos2 x) = 0.
Removing the brackets and collecting like terms, we get 3sin2 x – sin x cos x – 4 cos2 x = 0.
Since the values 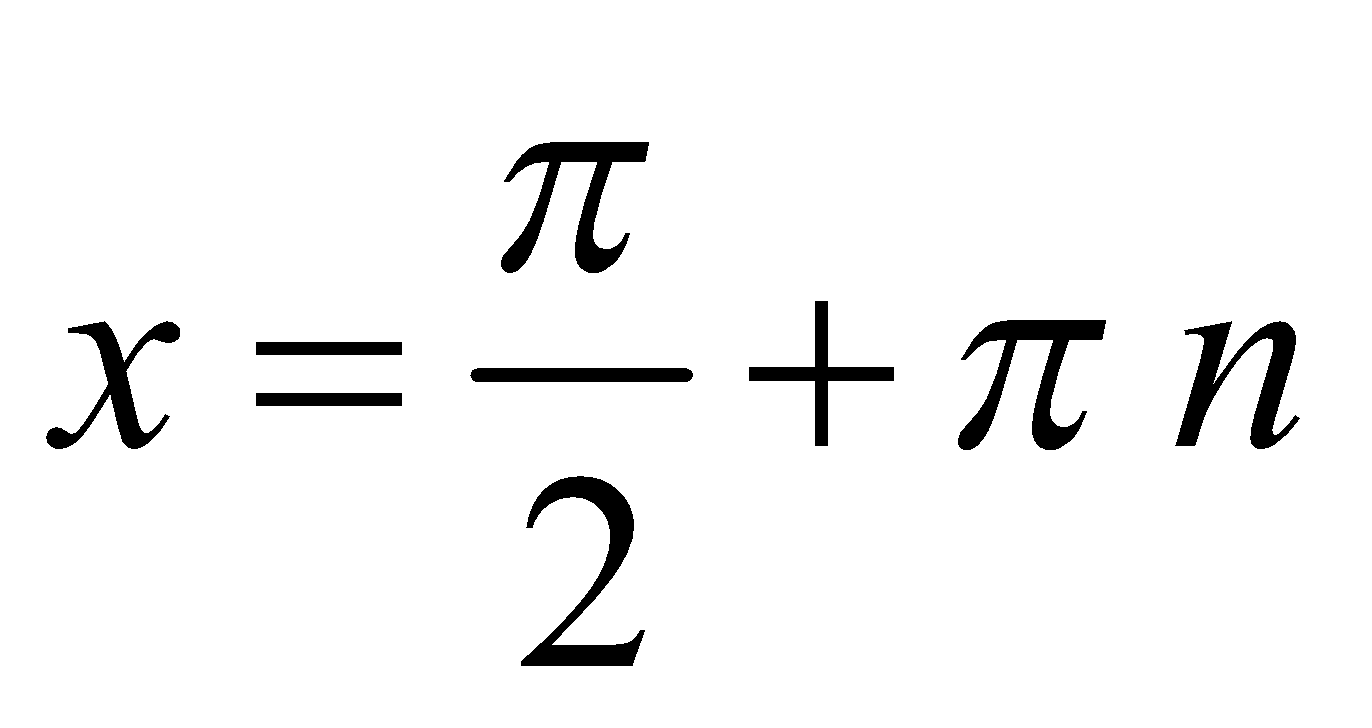 are not roots of the equation and cos x ≠ 0, we divide both sides of the equation by cos2 x : 3 tan2 x – tan x – 4 = 0,
are not roots of the equation and cos x ≠ 0, we divide both sides of the equation by cos2 x : 3 tan2 x – tan x – 4 = 0,
Whence tan x = –1, 
and 
Answer : 
SOLVING EQUATIONS BY INTRODUCING AN AUXILIARY ARGUMENT
Equations of the form a sin x + b cos x = c is solved by dividing the two sides of equation by 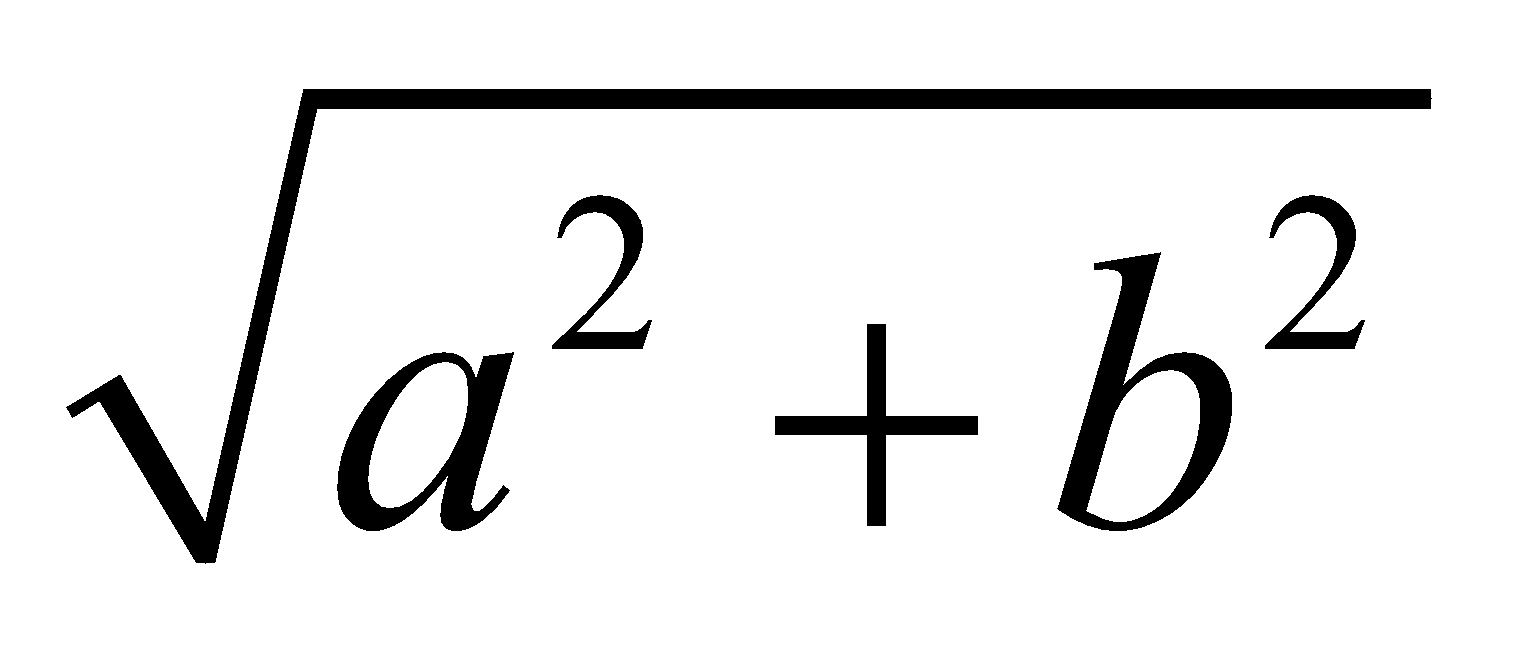 and substituting
and substituting 
Example :
Solve the equation sin x + cos x = 
Solution :
Answer :  :
:
SOLVING EQUATIONS BY TRANSFORMING A SUM OF TRIGONOMETRIC FUNCTIONS INTO A PRODUCT
We take the help of the formulae sin C + sin D = ......etc.
Example :
Solve the equation cos 3x + sin 2x – sin 4x = 0
Solution :
cos 3x + (sin 2x – sin 4x) = 0
Transforming the expression in brackets into product form we obtain
cos 3x + (–2 sin x cos 3x) = 0, or cos 3x (1 – 2 sin x) = 0
The last equation is equivalent to the collection of equations
cos 3x = 0 or 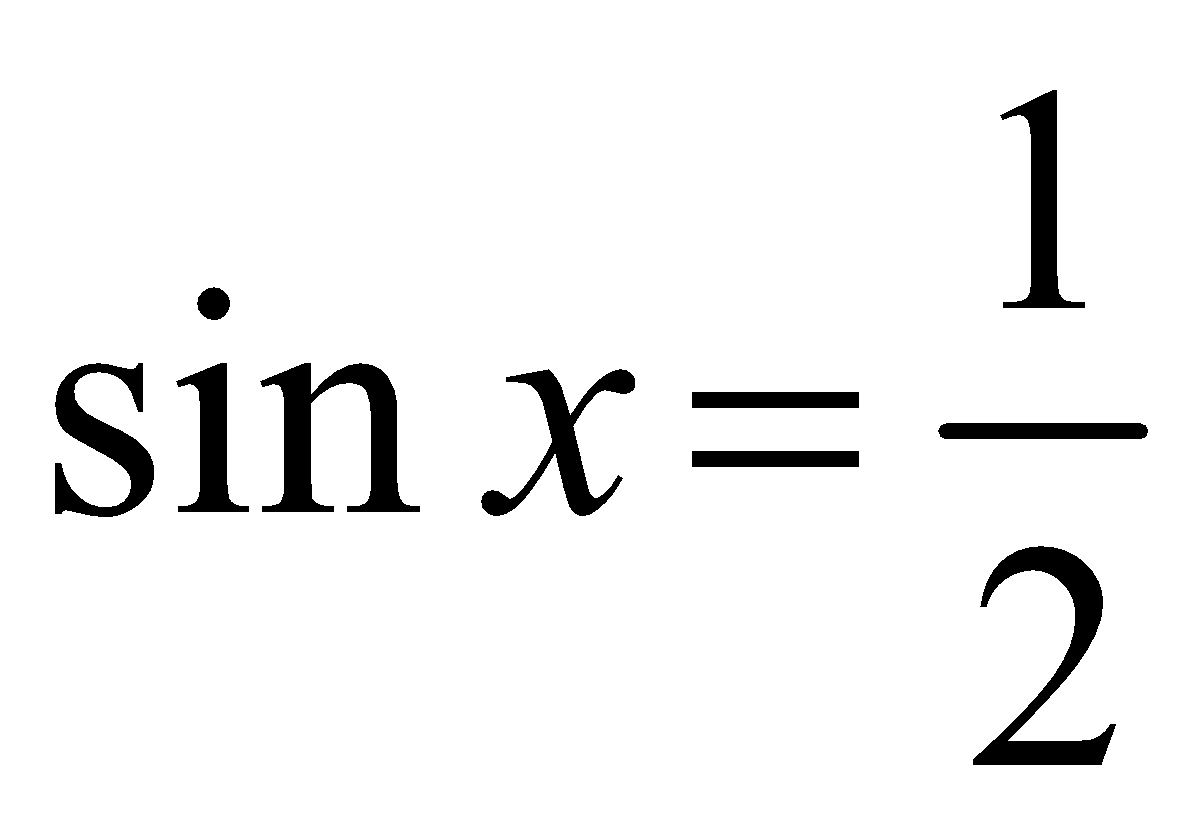
Consequently, 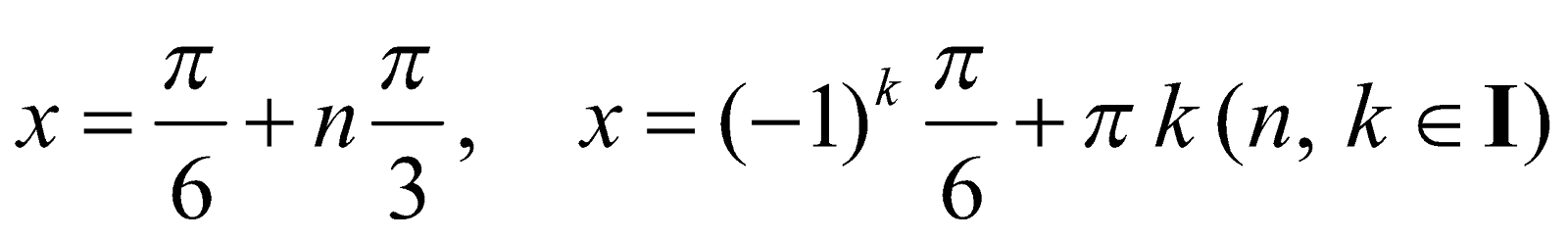 .
.
The set of solutions 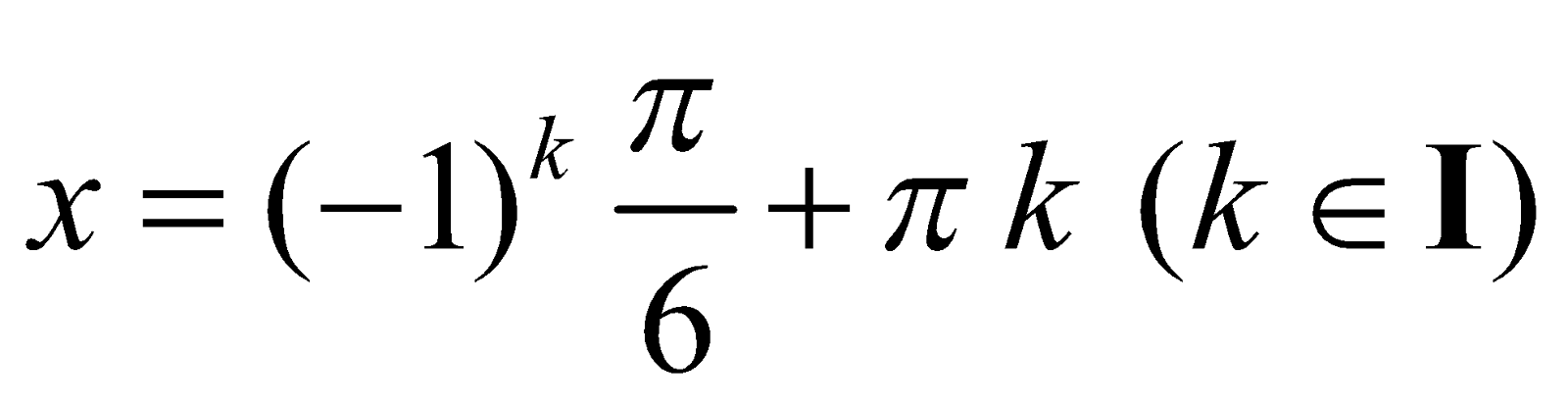 belongs entirely to the set of solutions
belongs entirely to the set of solutions 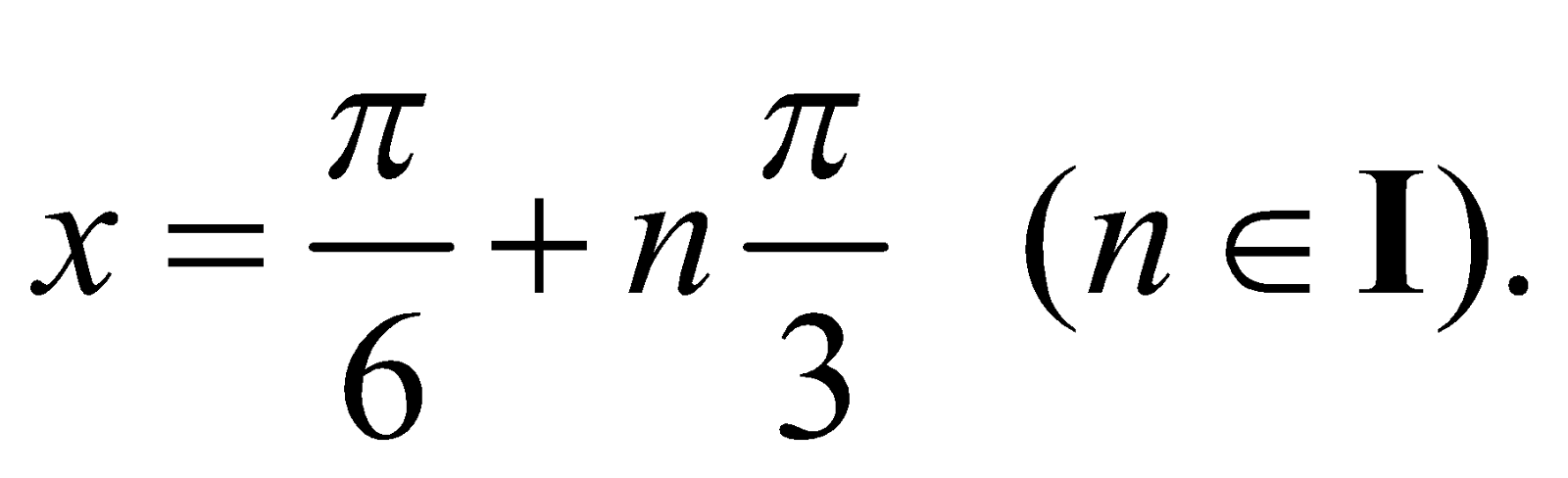
Therefore this set alone remains as a set of solutions.
Answer : 
SOLVING EQUATIONS BY TRANSFORMING A PRODUCT OF TRIGONOMETRIC FUNCTIONS INTO A SUM
We use the set of formulae 2 sin A sin B = ..........etc.
Example :
Solve : sin 5x cos 3x = sin 6x cos 2x.
Solution :
We apply formula of 2 sin A cos B to both sides of the equation :
Answer : 
SOLVING EQUATIONS WITH THE USE OF FORMULAS FOR LOWERING A DEGREE
Example :
Solve the trigonometric equation sin2 x + sin2 2x = 1
Solution :
We have 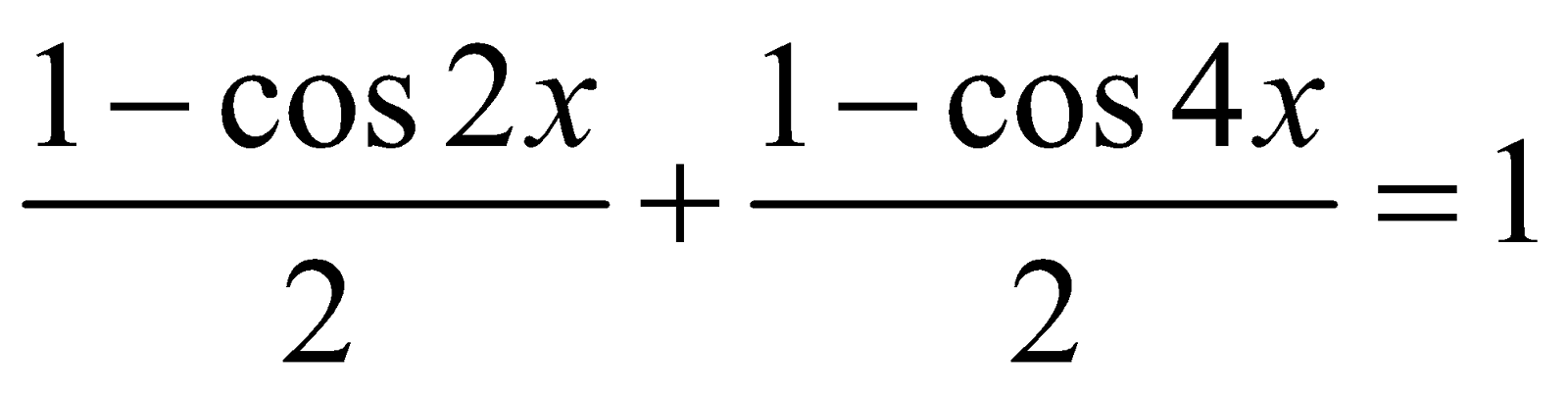
The last equation is equivalent to the collection of two equations
(a) cos 3x = 0, 
 n ∈ I.
n ∈ I.
(b) cos x = 0,  n ∈ I.
n ∈ I.
The set of the solutions of equation (b) is a subset of the set of solutions of (a) and, therefore in the answer we write only roots of equation (a).
Answer : 
SOLVING EQUATIONS WITH THE USE OF HALF ANGLE FORMULAS
Example :
Solve : 
Solution :
cos x – (1 – cos x) = 0 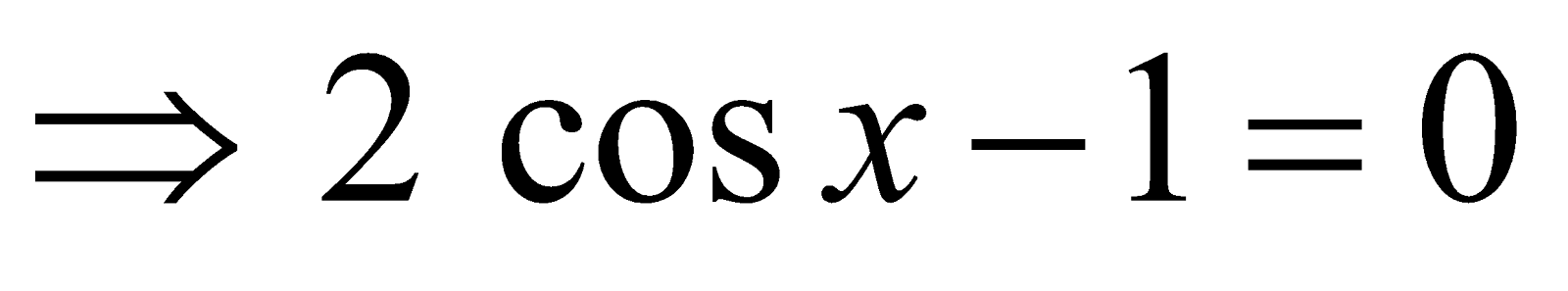
Answer : 
SOLVING EQUATIONS WITH THE USE OF FORMULAS FOR DOUBLE AND TRIPLE ARGUMENTS
Example 1 :
Solve : 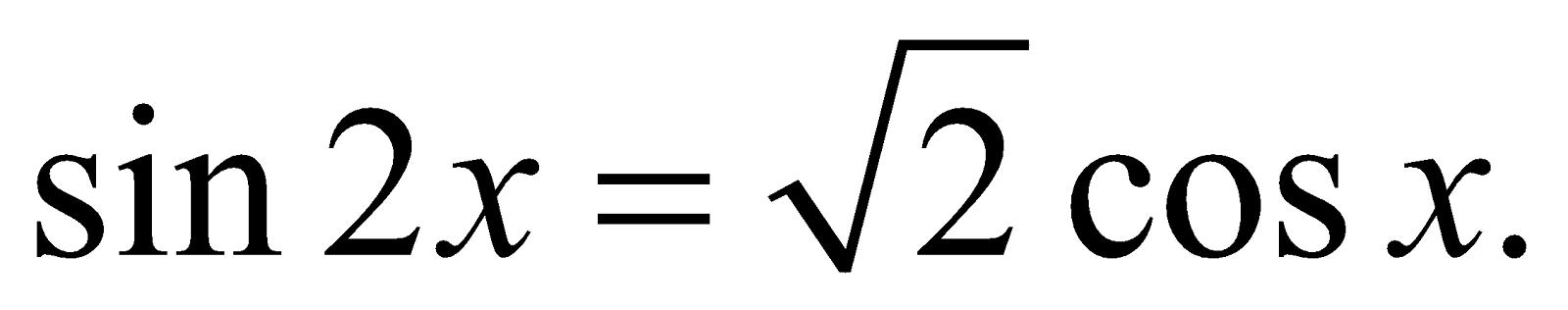
Solution :
Using formula, we obtain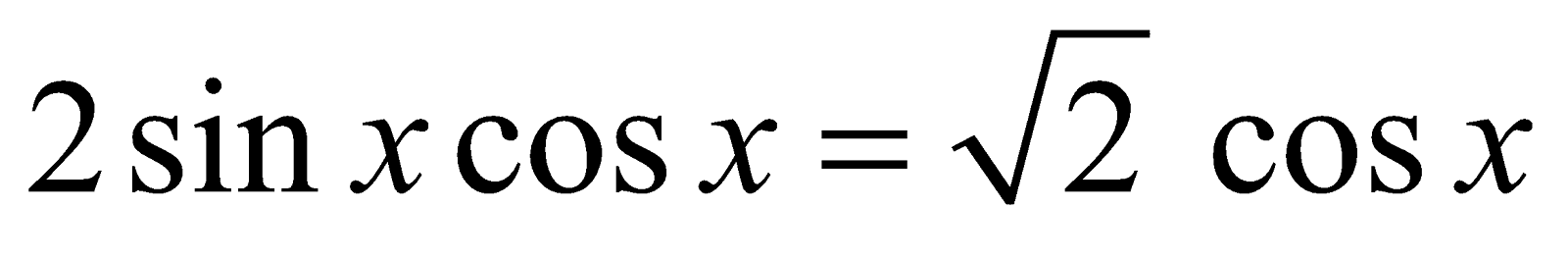
It is impossible to divide both sides of the equation by cos x since it would lead to the loss of solution which are roots of the equation cos x = 0.
We transfer to the left - hand side and get
to the left - hand side and get
Answer : 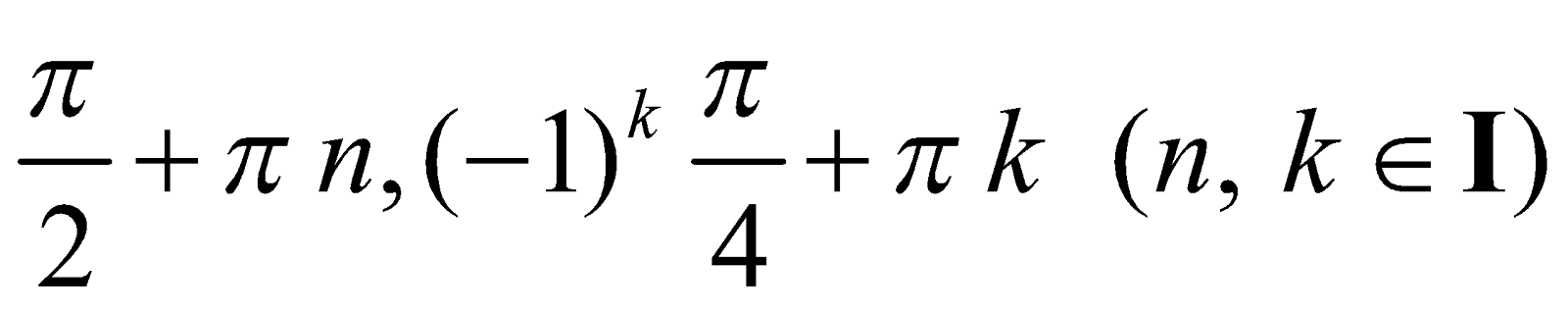
Example 2 :
Solve the equation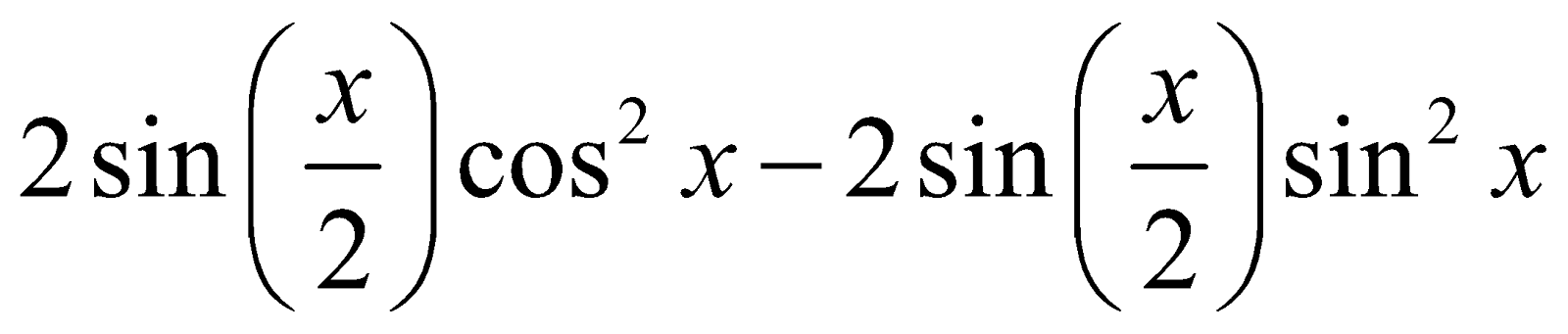

Solution :
The given equation is rewritten as
Replacing the expression ,  we get
we get
Answer : 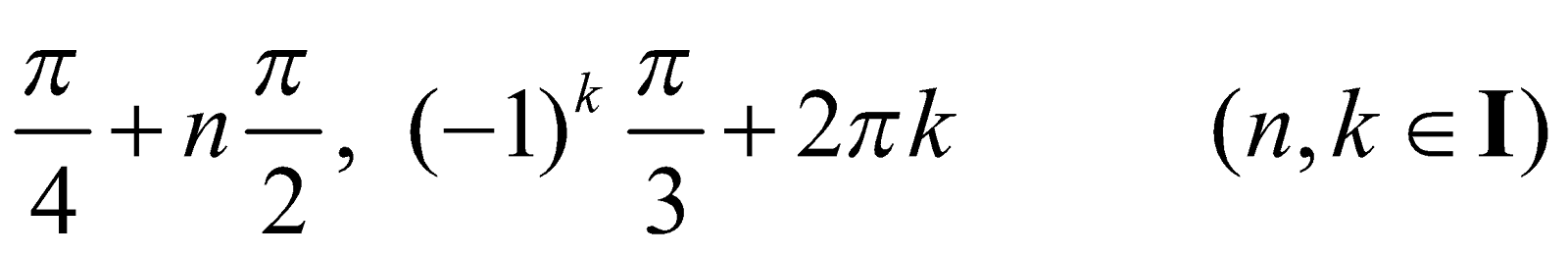
SOLVING EQUATIONS BY A CHANGE OF VARIABLE
- Equations of the form P (sin x ± cos x, sin x cos x) = 0
Where P (y, z) is a polynomial, can be solved by the substitution.
cos x ± sin x = t ⇒ 1 ± 2 sin x cos x = t2.
Let us consider an example .
Example :
Solve the equation sin x + cos x = 1 + sin x cos x
Solution :
We introduce the substitution sin x + cos x = t.
Then (sin x + cos x)2 = t2,
1 + 2 sin x cos x = t2  sin x cos x
sin x cos x
The initial equation in new variable is
i.e., sin x + cos x = 1, 
Answer : 
- Equation of the from a sin x + b cos x + d = 0,
Where a, b, and d are real numbers, and a, b ≠ 0, can be solved by the change
Note that such equations can be solved by dividing by  as well.
as well.
Example : Solve the equation 3 cos x + 4 sin x = 5
Solution :
Answer : 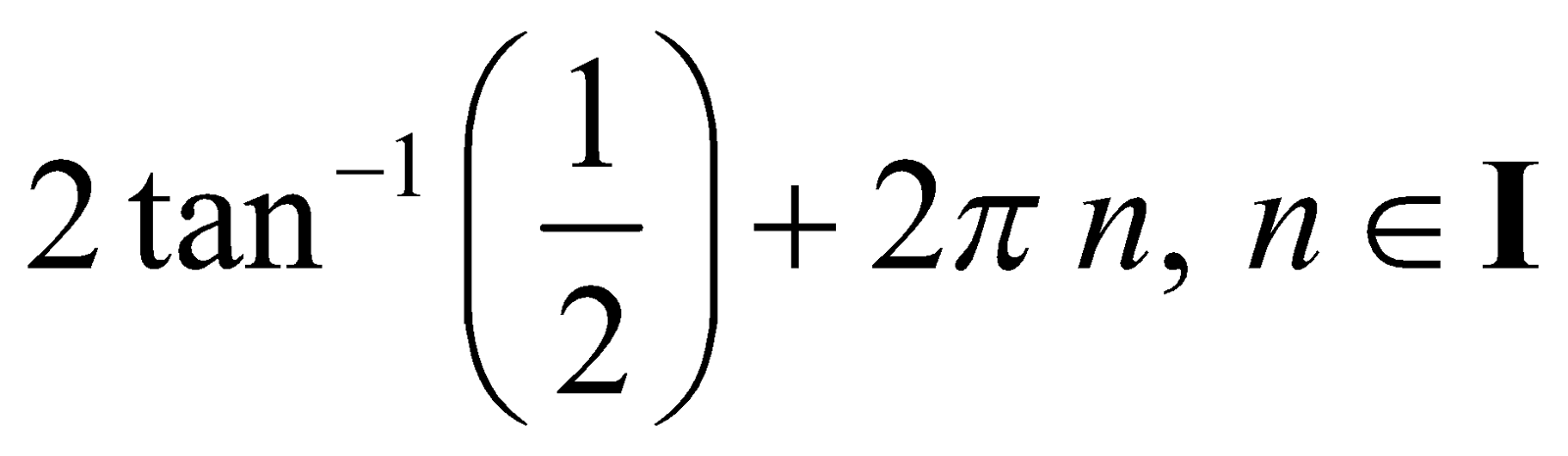
- Many equation can be solved by introducing a new variable :
Example :
Solve the equation
Solution :
The given equation can be written as
We introduce the substitution sin 2x cos 2x = y.
The last equation assumes the form 2y2 + y – 1 = 0, or 
We pass to the variable x and obtain
- sin 2x cos 2x = –1
2 sin 2x cos 2x = –2
sin 4x = –2
- sin 2x cos 2 x =
sin 4x = 1
Answer : 
SOLVING EQUATIONS WITH THE USE OF THE BOUNDEDNESS OF THE FUNCTIONS sin x AND cos x
We normally use the following extreme values of the functions.
Example :
Solve the equation
Solution :
Since the functions  and cos x have the greatest value equal to 1, their sum is equal to 2 only if
and cos x have the greatest value equal to 1, their sum is equal to 2 only if  and cos x = 1 simultaneously,
and cos x = 1 simultaneously,
i.e., 
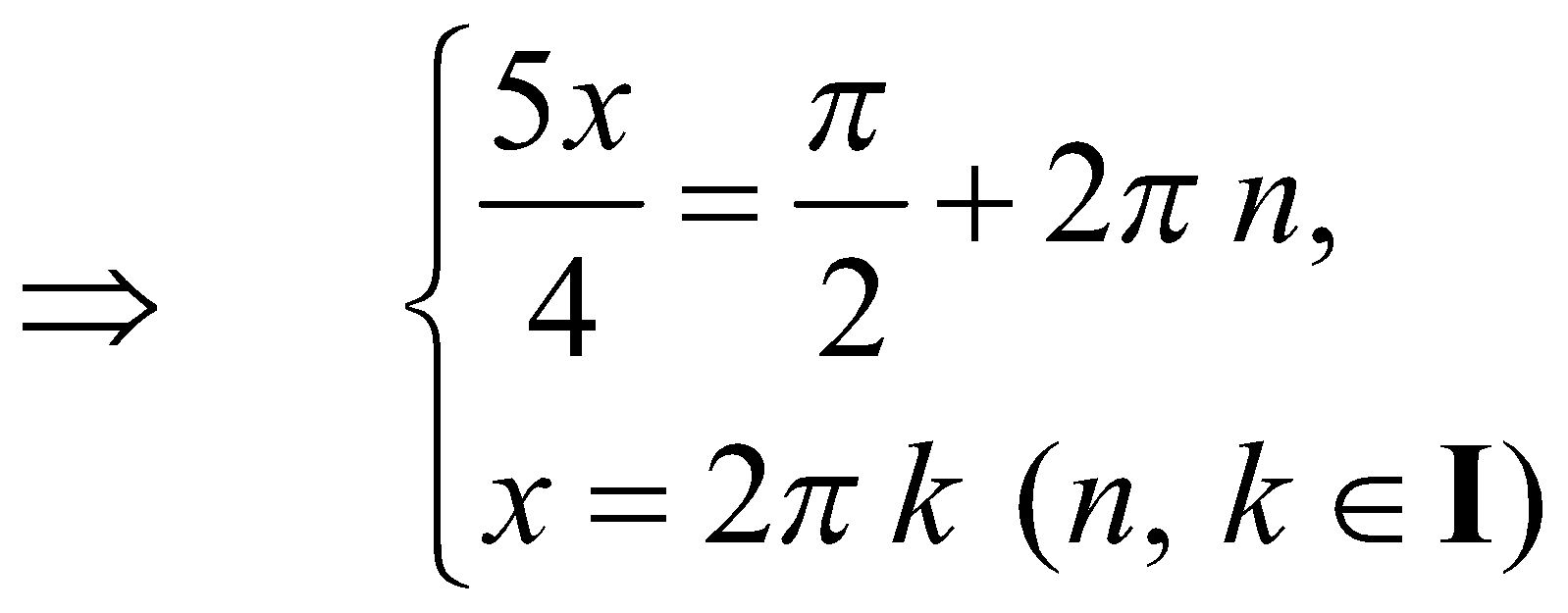
∴ 
Since k∈I, it follows that n = 1 + 5 m (m∈I), and then
x = 2 + 8π m, m∈I.
Answer : 2π + 8π m, m∈I
TRIGONOMETRIC SYSTEMS
Example :
Solve the following system of equations
Solution :
We transform the second equation and get 3 sin x cos y – sin y cos x = 0
Substituting now the value of the product sin x cos y form the first equation into the equation obtained, we get a system
 ...(1)
...(1)
Adding together the equations of system (1) and then subtracting the first equation from the second, we get a system which is equivalent to system :
Hence we have  ...(3)
...(3)
and 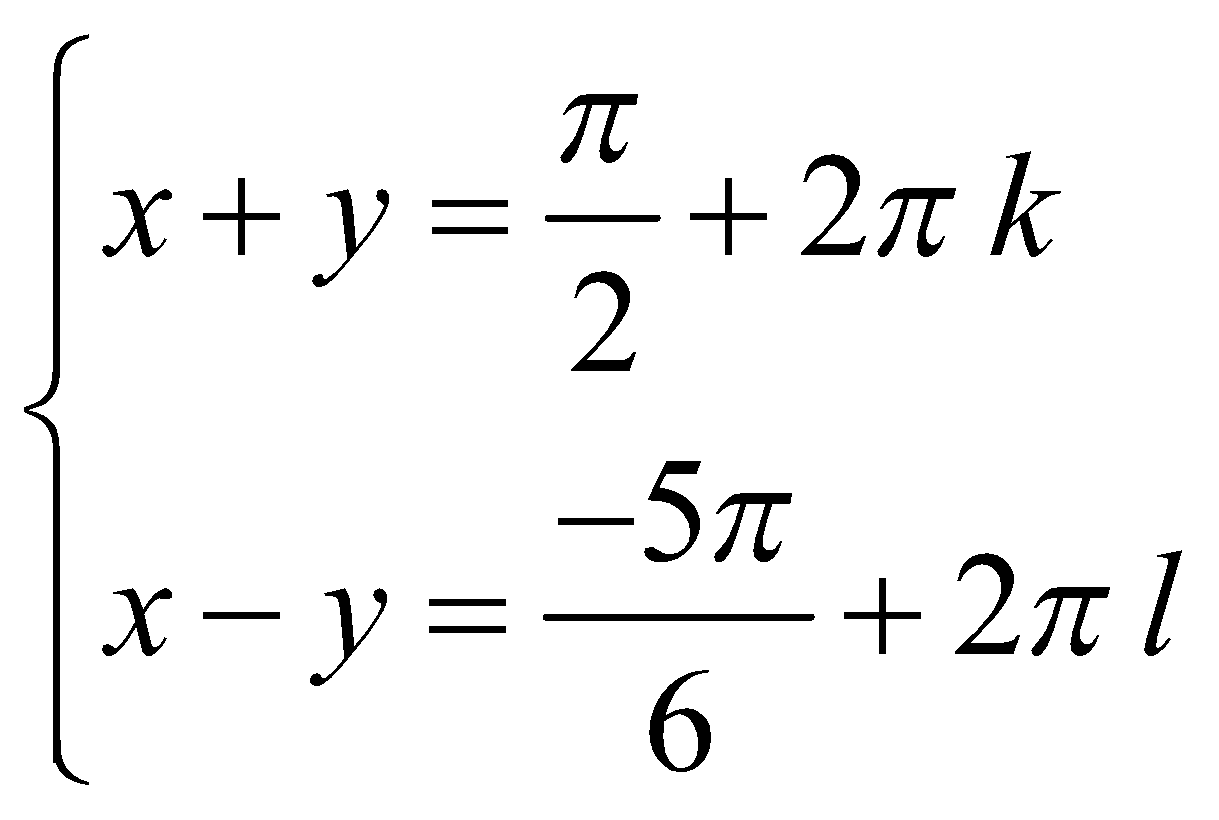 ...(4)
...(4)
From system (3) we find From system (4) we find letters
Pay attention to the fact that the integers by which 2π is multiplied in (3) must be represented by different letters (say, k and l), since these sets are not interconnected. If the same letter is used in these sets, solutions will be lost.
SOLUTION OF TRIGONOMETRIC INEQUATIONS
WORKING PROCEDURE
- We try to convert the inequation in direct form, e.g.,
sin x > a or cos x < b or c ≤ tan x ≤ d, etc
- Draw graph of the involved trigonometric function for one period nearest to origin, in general – π to π or 0 to 2π for sin x and cos x and
to
for tan x
- Identify the region in the graph, which satisfies the given inequality and find out corresponding interval(s) of x on x – axis
- If the solution contains more than one interval of x, try to change them into one interval by shifting the graph slightly left or right
- Add to the interval obtained above 2nπ in case of sin x and cos x inequalities and nπ in case of tan x inequality, which is the general solution.
Example : We solve sin x > 0
Solution : We draw graph of y = sin x in [–π, π]. Clearly
sin x > 0 is represented by 0 < x < π in the graph. So principal solution is 0 < x < π and the general solution is 2nπ < x < 2nπ + π. We represent the solution as following:
sin x > 0 is represented by 0 < x < π in the graph. So principal solution is 0 < x < π and the general solution is 2nπ < x < 2nπ + π. We represent the solution as following:







