Indefinite Integration | Mathematics Notes for IITJEE Main

INDEFINITE INTEGRATION

Integration is the inverse process of differentiation The process of finding f(x), when its derivative f’(x) is given, is known as integration.

PRIMITIVE OR ANTIDERIVATIVE

F(x) is a primitive of a function f(x) if F’(x) = f(x).

If F(x) is a primitive of f(x) then F(x) + C, where C is a constant is also a primitive. Thus, if a function possesses a primitive then it possess infinitely many primitives.

A function may or may not possess a primitive.

The collection of all primitives of a function f(x) is called its indefinite integral, denoted by ∫f(x) dx. Thus

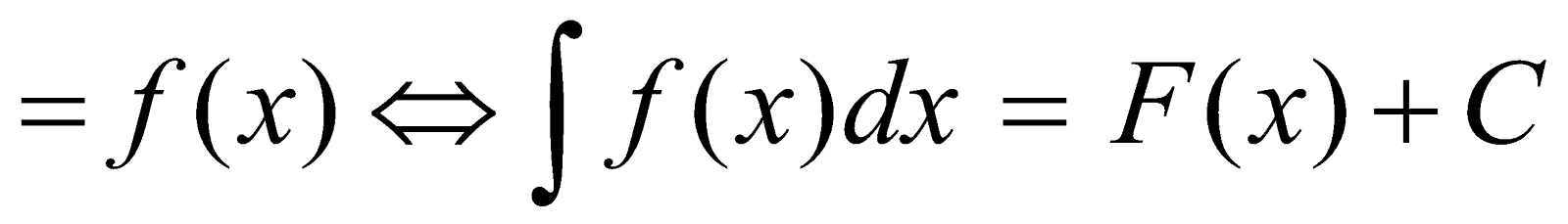
C is called constant of integration.

ELEMENTARY RESULTS

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 

RULES OF INTEGRATION

1. 
2. 
3. 
4. 
5. If then
6. 
7. 

INTEGRATION BY SUBSTITUTION

If φ(x) is continuously differentiable function, then to evaluate we substitute and giving .

SOME RECOMMENDED SUBSTITUTIONS

• If  a2 + x2, put x = a tan θ
• If  a2 – x2, put x = a sin θ
• If  x2 – a2, put x = a sec θ
• If  put x = a cos 2θ
• If
• If .

IMPORTANT RESULTS USING STANDARD SUBSTITUTION

1. 
2. 
3. 
4. 
5. 
6. 
7. 

INTEGRATION OF FUNCTIONS USING ABOVE STANDARD RESULTS

FORM 1

Integral of type ,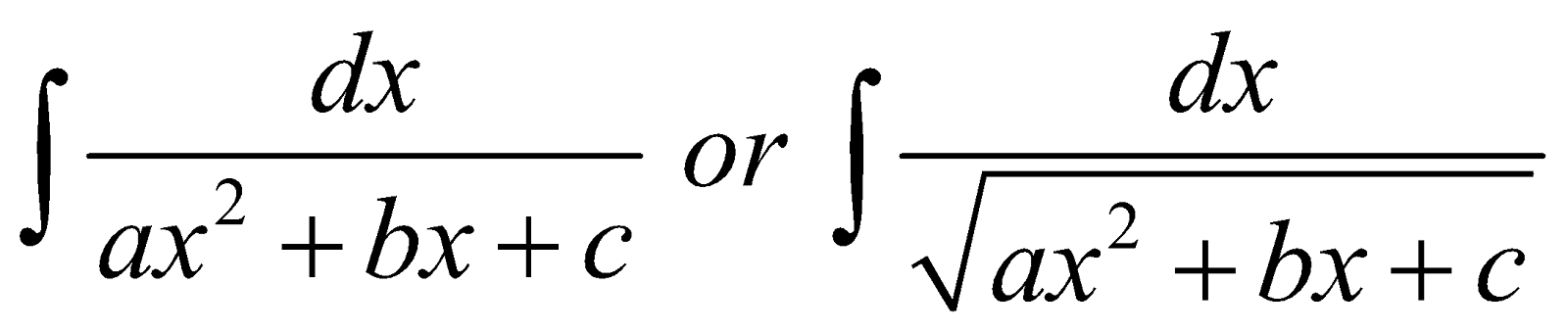

Express 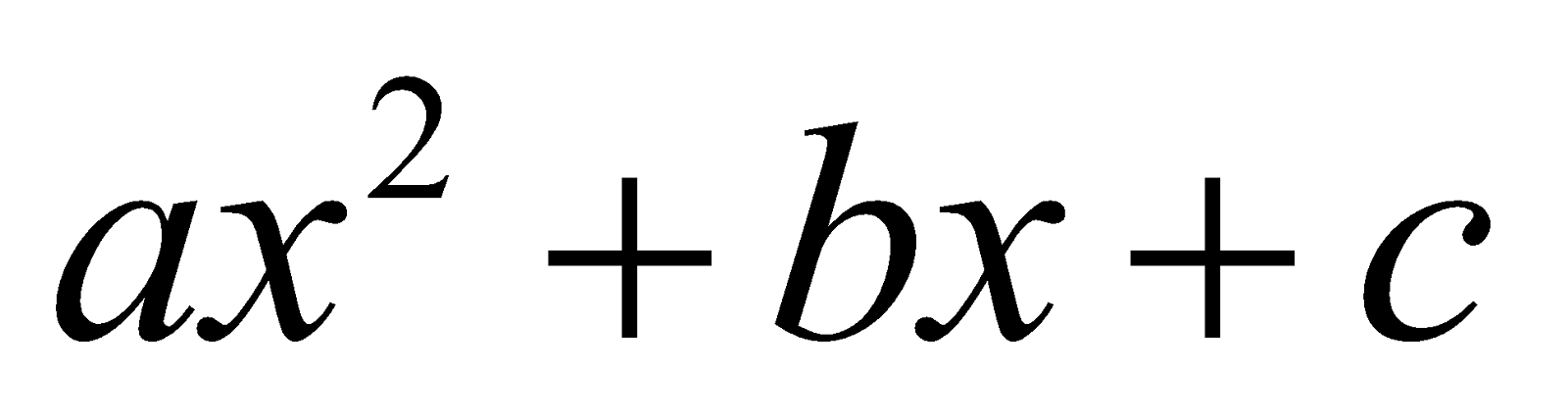as sum or difference of two squares i.e.,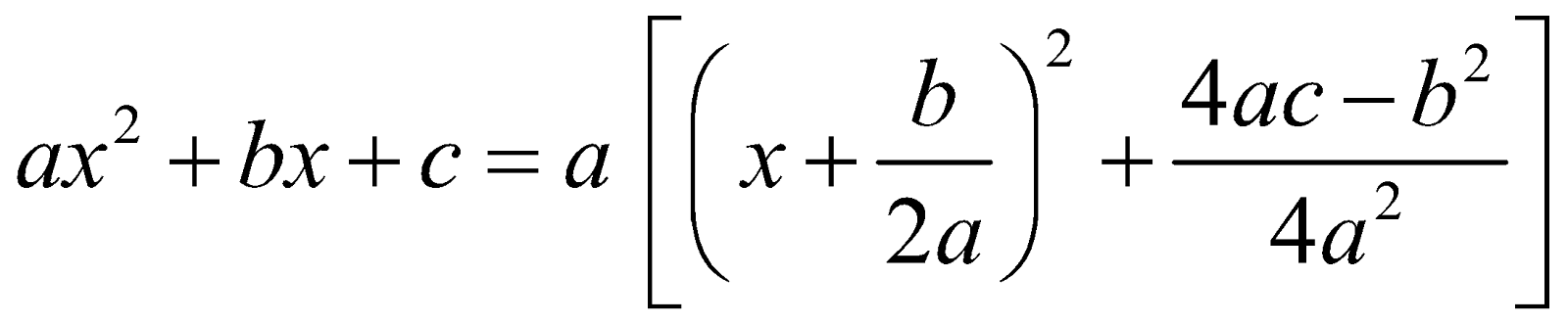  

Then use appropriate formula.

FORM 2

Integral of type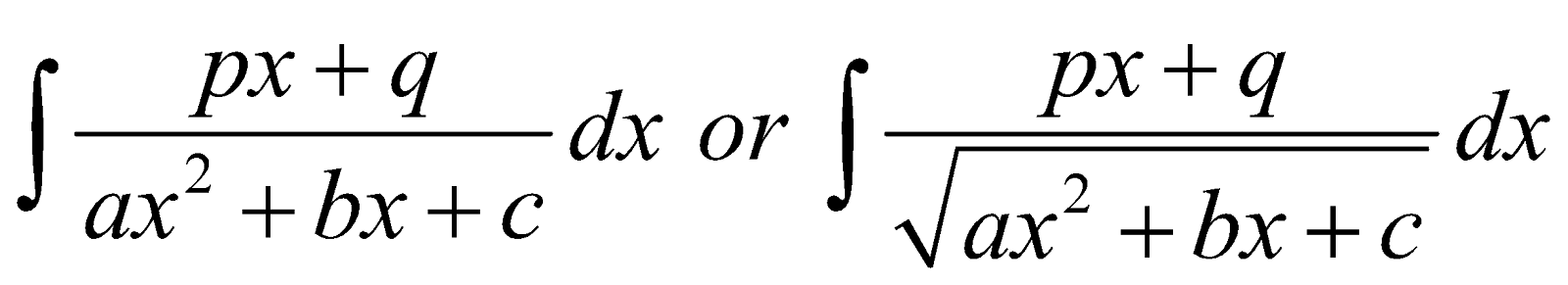  

Express px + q in the form

That is,

Evaluate λ and μ by equating coefficients of x and x°. The integral reduces to known forms.

FORM 3

Integral of the type when P(x) is a polynomial of degree 2 or more.

First carryout the division and express it in the form

Where R(x) is a linear expression or constant Then the integral reduces to known forms

FORM 4

Integrals of the forms

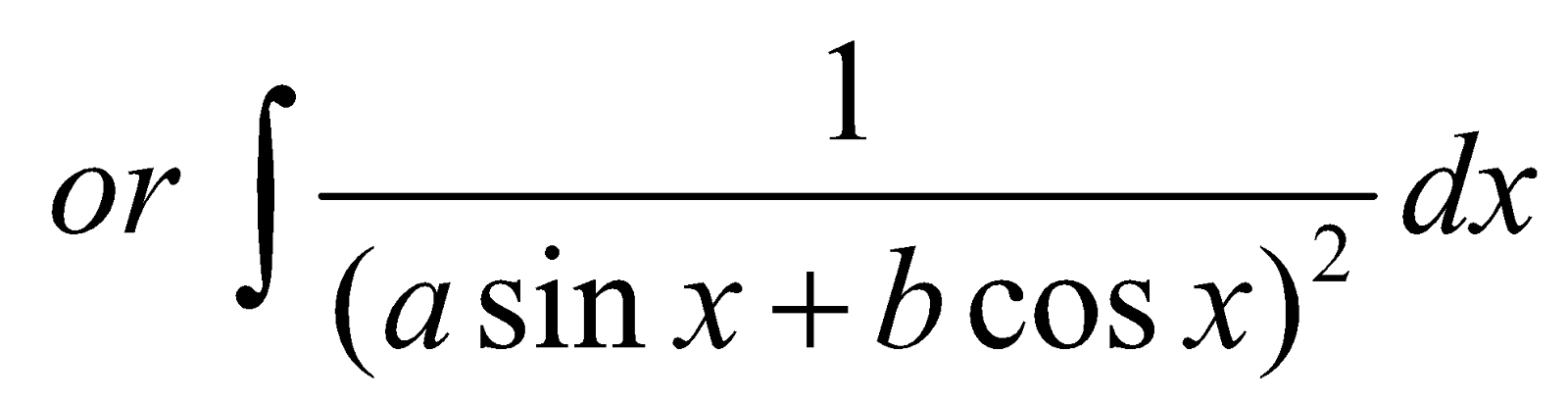
PROCEDURE

For each of the above integrals, we proceed as following :

1. Divide Numerator and Denominator by cos2x
2. Replace sec2x, If any in denominator by 1+tan2x
3. Substitute tan x = t,  sec2 x dx  = dt

FORM 5

Integrals of the form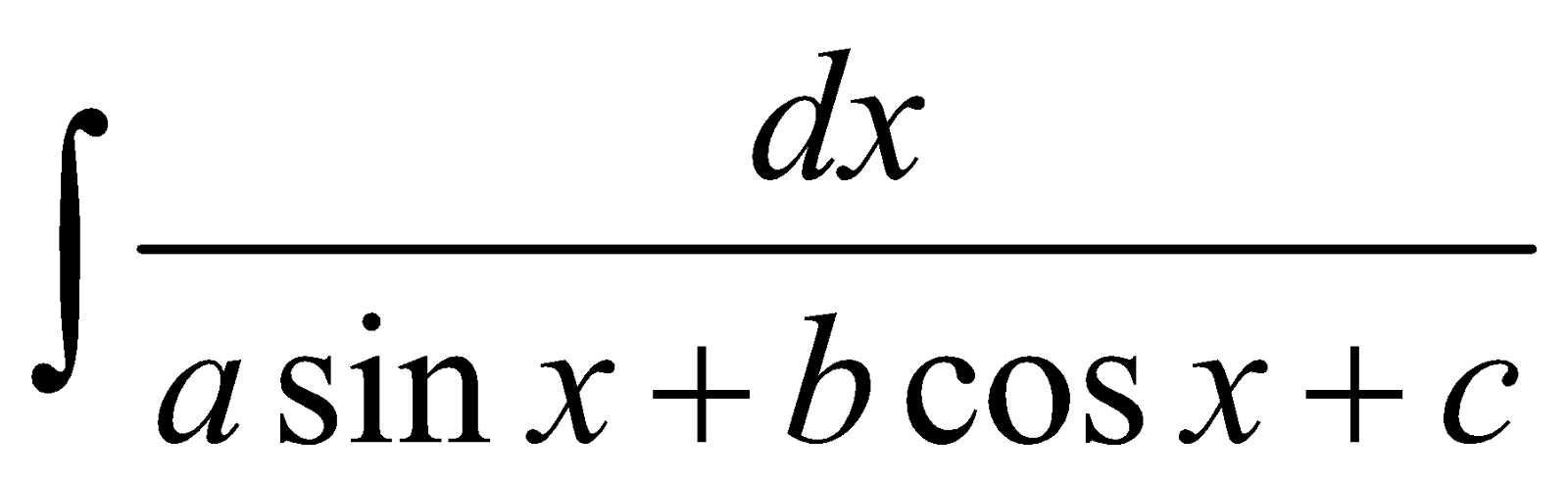

PROCEDURE

To evaluate such integrals we proceed as follows

1. Replace sin x = and cos x =
2. Replace 1+ in numerator
3. Substitute

FORM 6

Integral of the form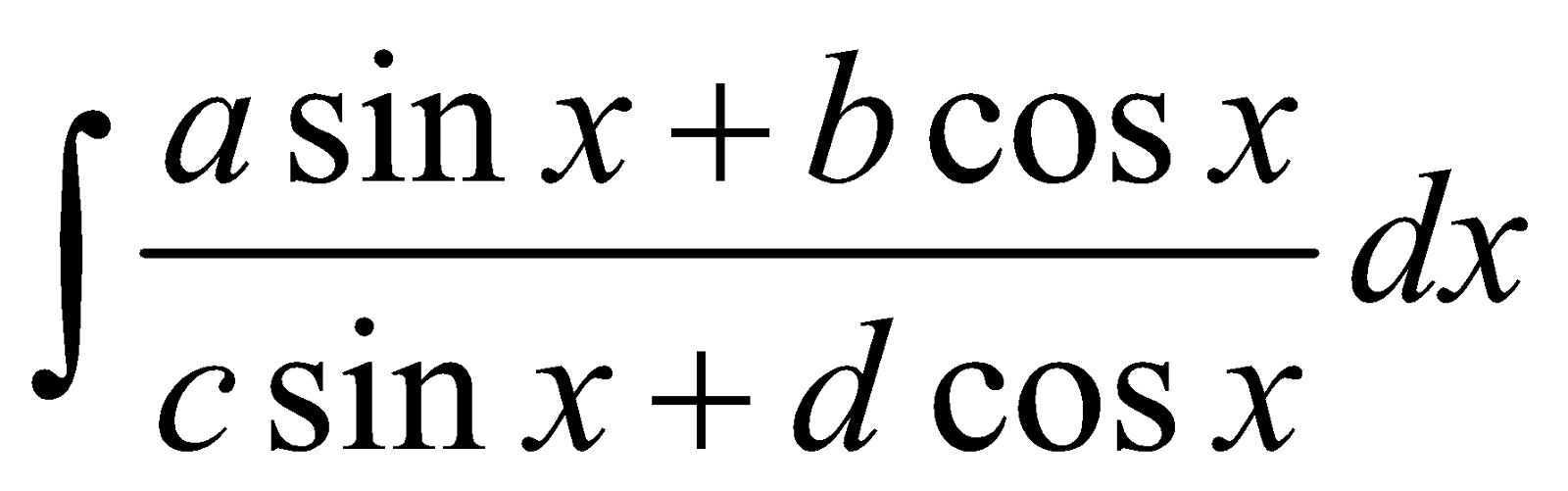

PROCEDURE

We proceed as follows

Express, Numerator = λ (Denominator) + (Denominator)

That is a sin x + b cosx = λ (c sin x + d cosx) +

FORM 7

Integral of the form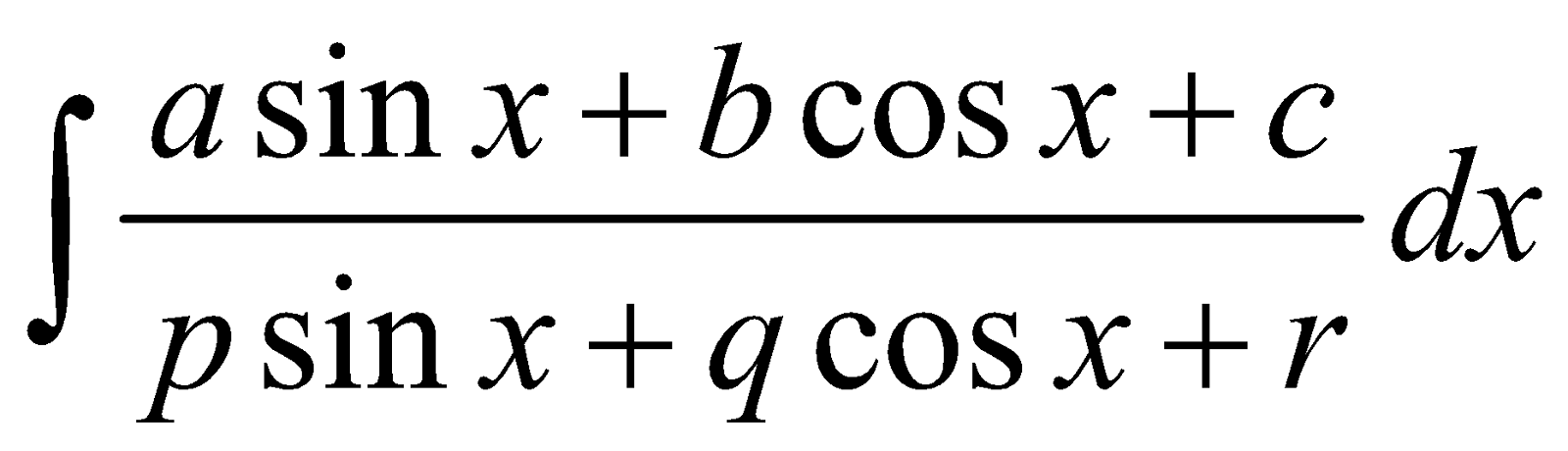

PROCEDURE

We proceed as following :

Express Numerator = λ (Denominator) + (Denominator) + ν

That is a sin x + b cos x + c = λ (psin x + q cos x +r) + (pcos x – qsin x) + ν

[Form 6 and form 7 differ in constant only]

INTEGRATION OF RATIONAL ALGEBRAIC FUNCTIONS USING PARTIAL FRACTIONS

Consider the integral of the type, where f(x) and g(x) are two rational polynomials of x. By decomposition of the fraction 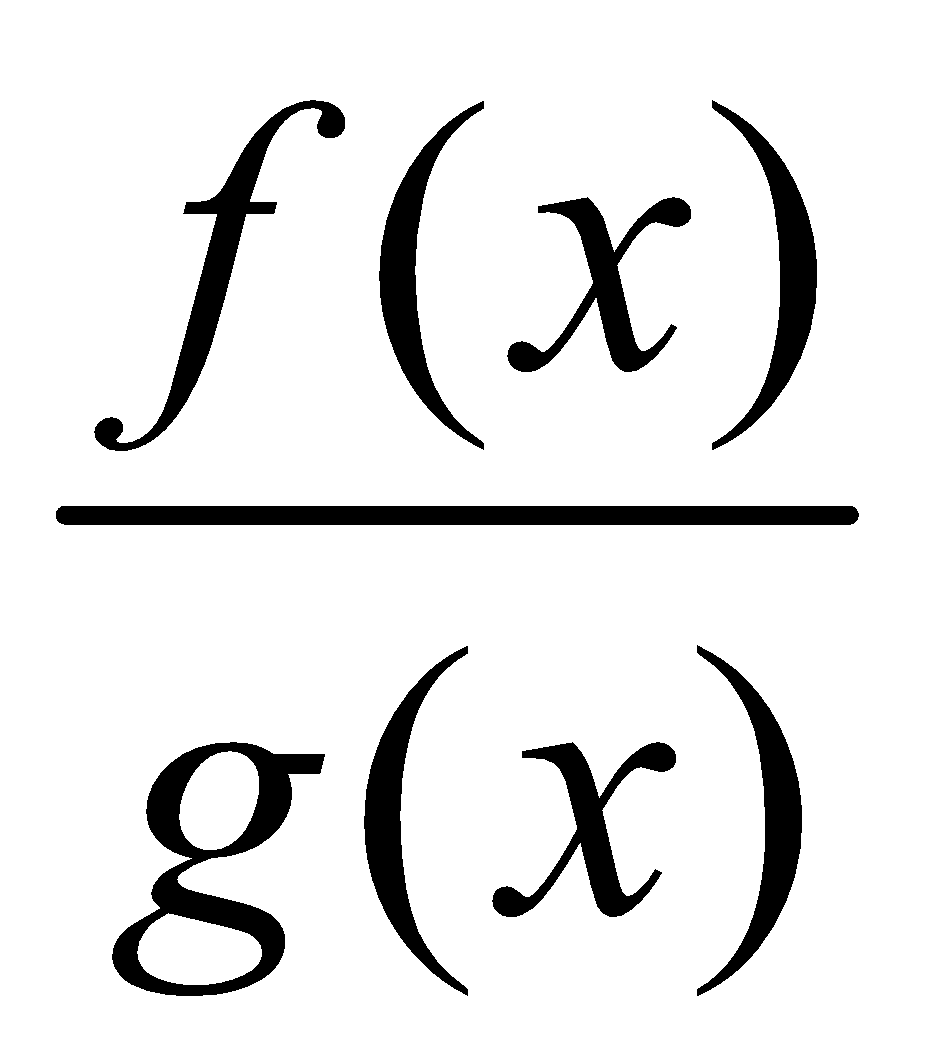 into partial fractions we may convert the integral into the forms already discussed.

To start with we assume that the degree of polynomial f(x) (the numerator) is less than the degree of g(x) (the denominator). In case it is not so, we may convert it in such form by carrying out actual division.

The partial fractions depend on the nature of the factors of denominator g(x).

CASE 1 : When g(x) is expressible as the product of non-repeated linear factors

Let g(x)  = (x – a1) (x – a2) (x – a3) ......... (x – an)

Express  

Where,  are constants and can be determined by equating the numerator from both the sides and substituting by equating the coefficients of different powers of x.

SHORTCUT FOR FINDING CONSTANT A1, A2 . . . . .

Alternatively, we may find the constants from the following

 

 

      

Trick : To find A1, Put x = a1 in numerator and denominator after deleting the factor x–a1, from denominator.

CASE 2 : When g(x) is expressible as the product of linear factors such that some of them are repeated (occur as  square or cube.........) Let g(x) = (x – a)k (x – a1) (x – a2) ......(x–an)

Express

Here, all the constants A1, A2, ....,  Ak, B1,  B2, ................, Bn can not be obtained using the method discussed in CASE(i).

However B1, B2, ....Bn  can be found using the same method thus.

;  

Also Ak can be found in the same way

Other constants A1, A2, ... Ak–1 must be determined by equating the coefficients of powers of x.

CASE 3 : g(x) contains quadratic factors, which are non-repeating

Let g(x) =

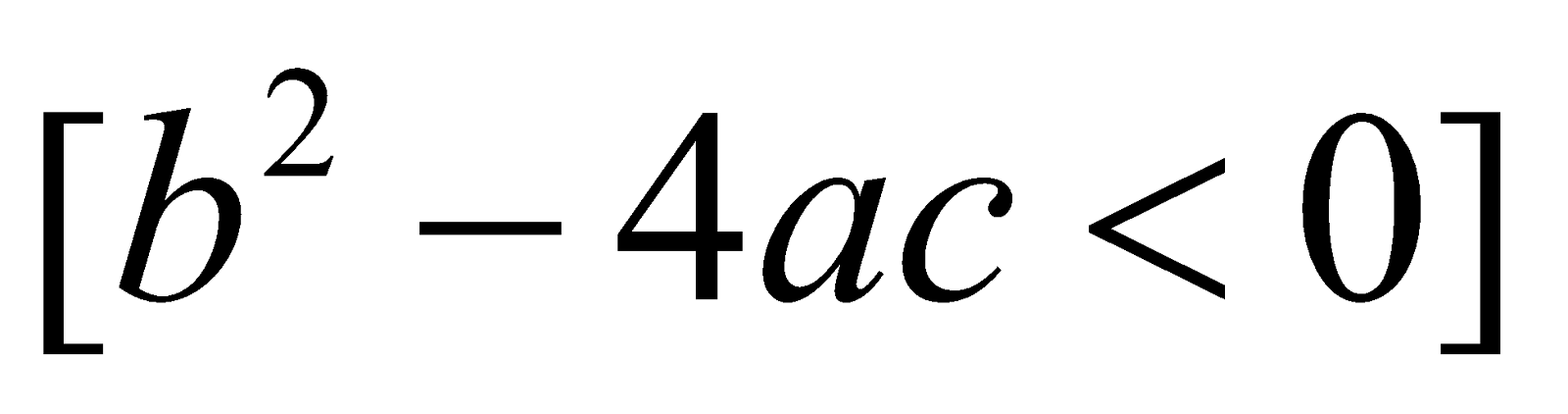
Express

Again A1, A2, ..........An can be obtained using method discussed in two previous cases A and B must be evaluated by equating the coefficients.

DERIVED FORMS

FORM 1

Integrals of the Form

1. Divide Numerator and Denominator by x2, we get

2. Substitute . Also on squaring
3. The integral becomes , which is one of standard forms.

Note : This type of integral has even powers of x only.

FORM 2

Integrals of the form

I =

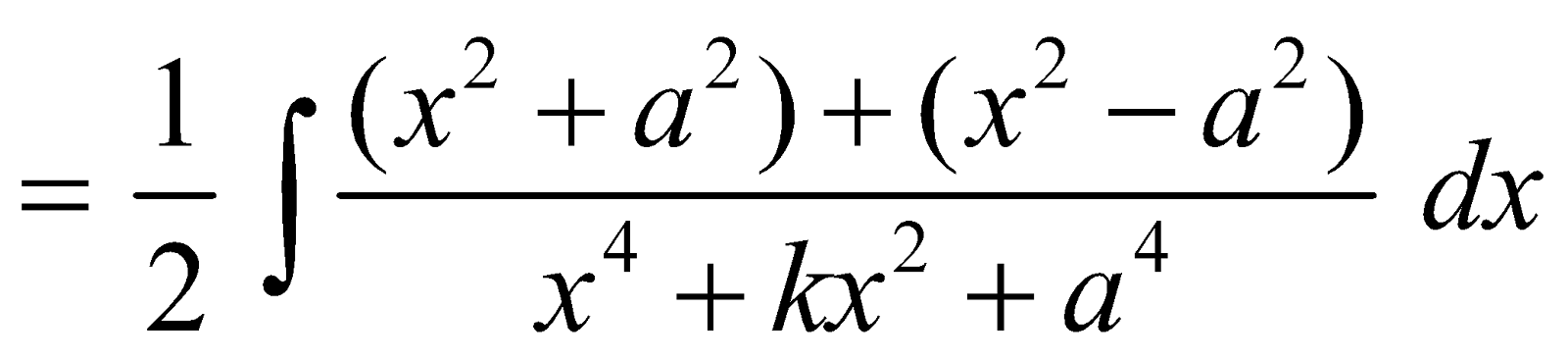
Now both the integrals can be evaluated as in form 1

FORM 3

Integrals of the form

I =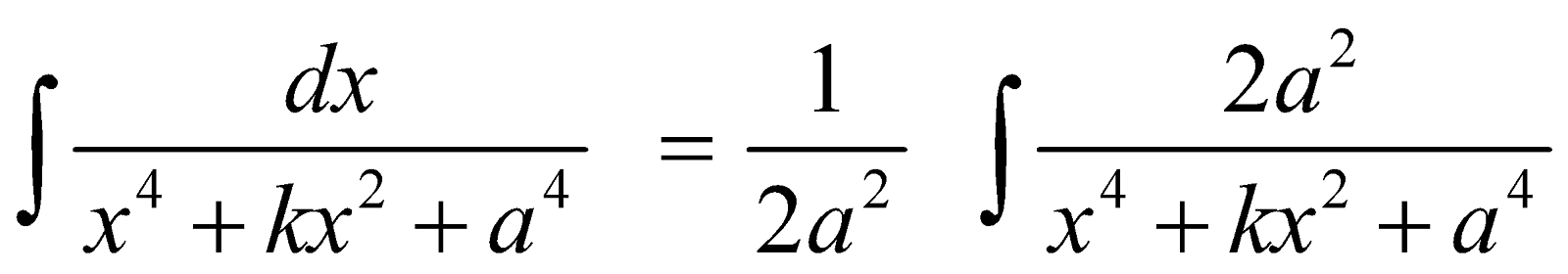

Now both the integral can be evaluated.

INTEGRATION BY PARTS

The formula of integration by parts is used to integrate the product of two functions.

If f(x) and g(x) be two integrable functions then

or

where, u and v are two integrable functions of x. More precisely.

  

SELECTION OF FIRST AND SECOND FUNCTION

1. Usually we use the following preference order for the first function.
   Inverse–Logarithmic–Algebraic–Trigonometric–Exponentials, the function on the left is normally chosen as the first function. In short we write ILATE.
2. If one of the functions is not directly integrable then we take it as the first function.
3. If there is no other function, then unity is taken as the second function.
4. If both the functions are directly integrable then the first function is chosen in such a way that its derivative vanishes easily or the function obtained in integral sign is easily integrable.

INTEGRALS OF THE FORM

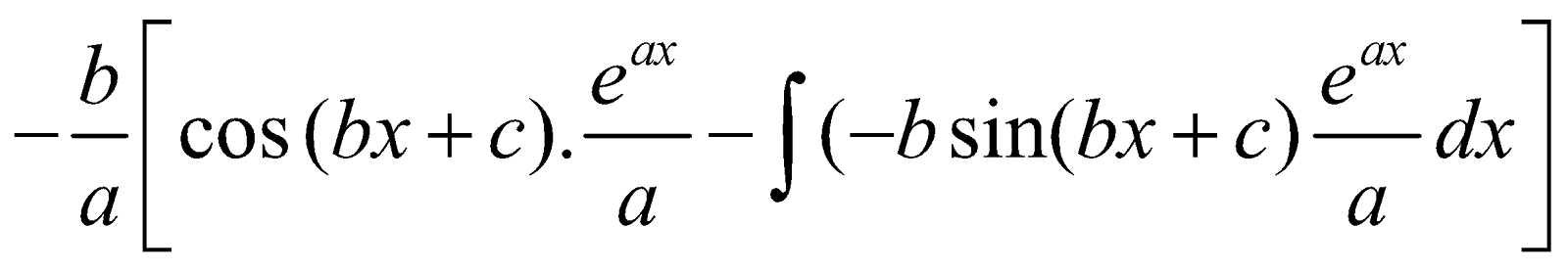
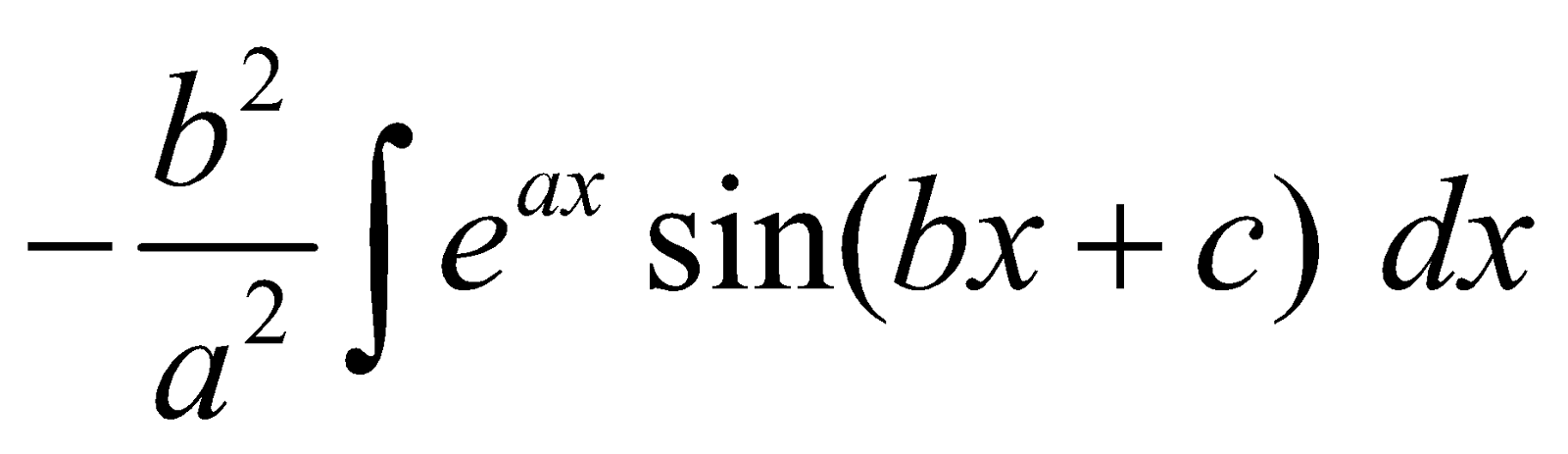
Let I =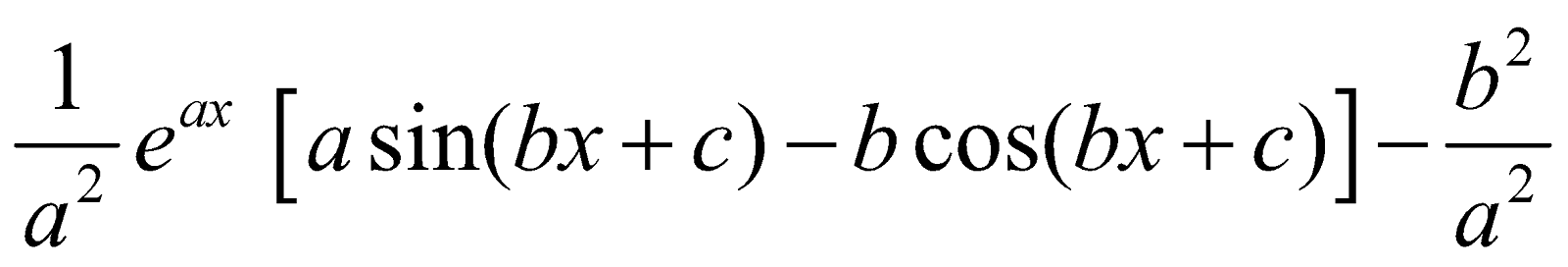

=  

    

=

I = I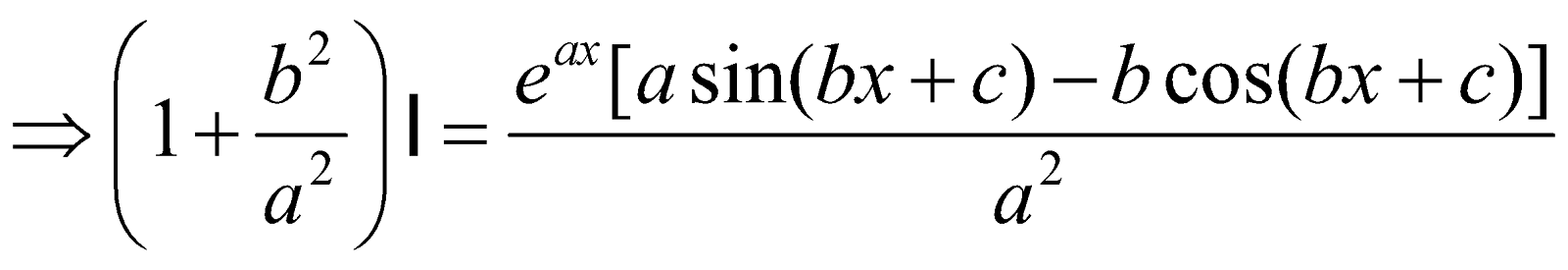

∴ I  = [K is constant of integration]

=

=  

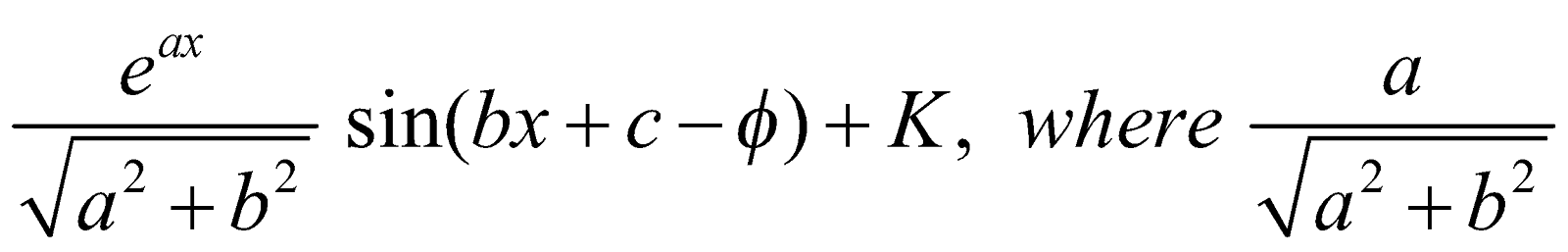
Similarly,  

where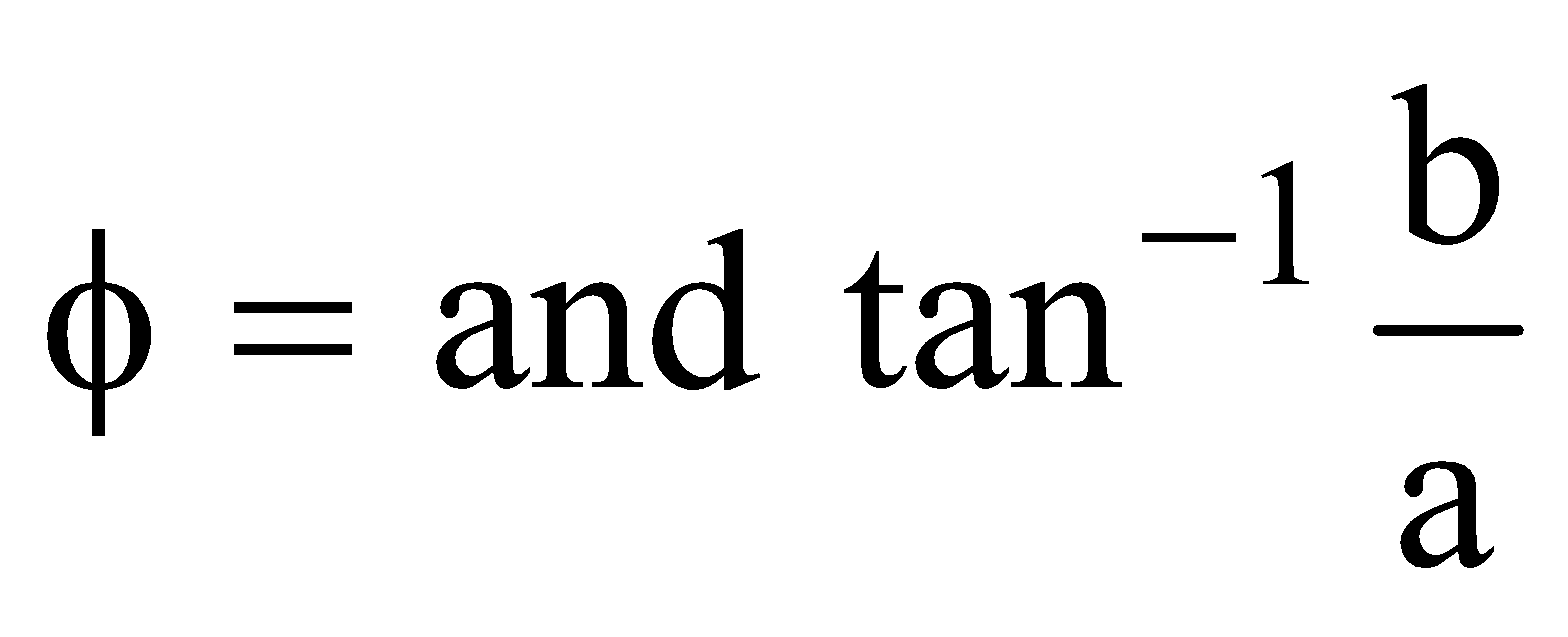  

INTEGRALS OF THE FORM

(I)   (II) (III)

Let I =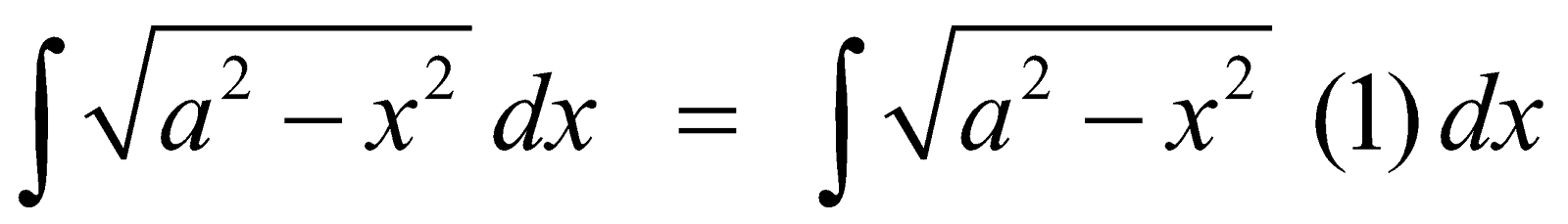

I

2 I =

⇒ I =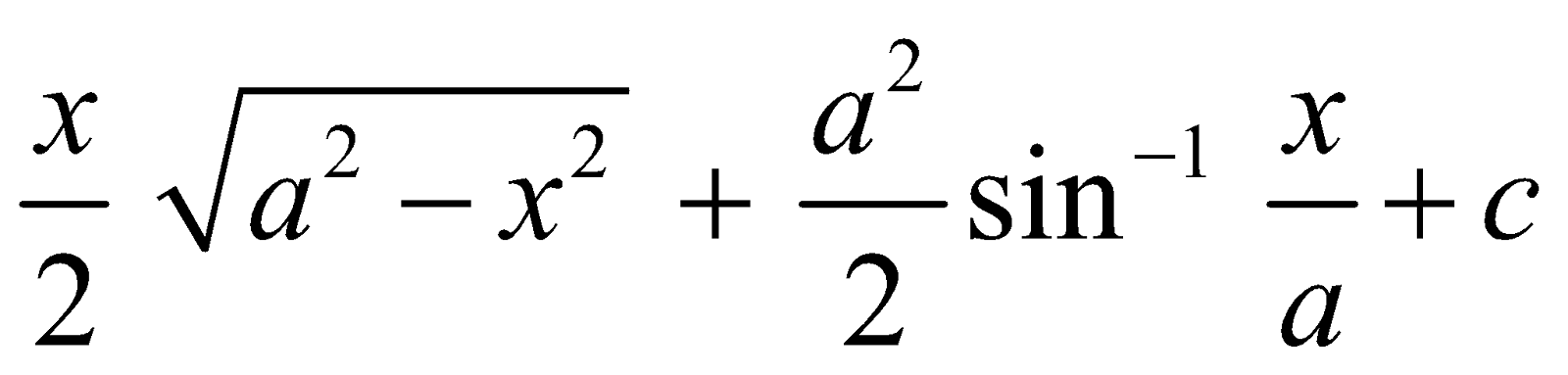

Similarly ,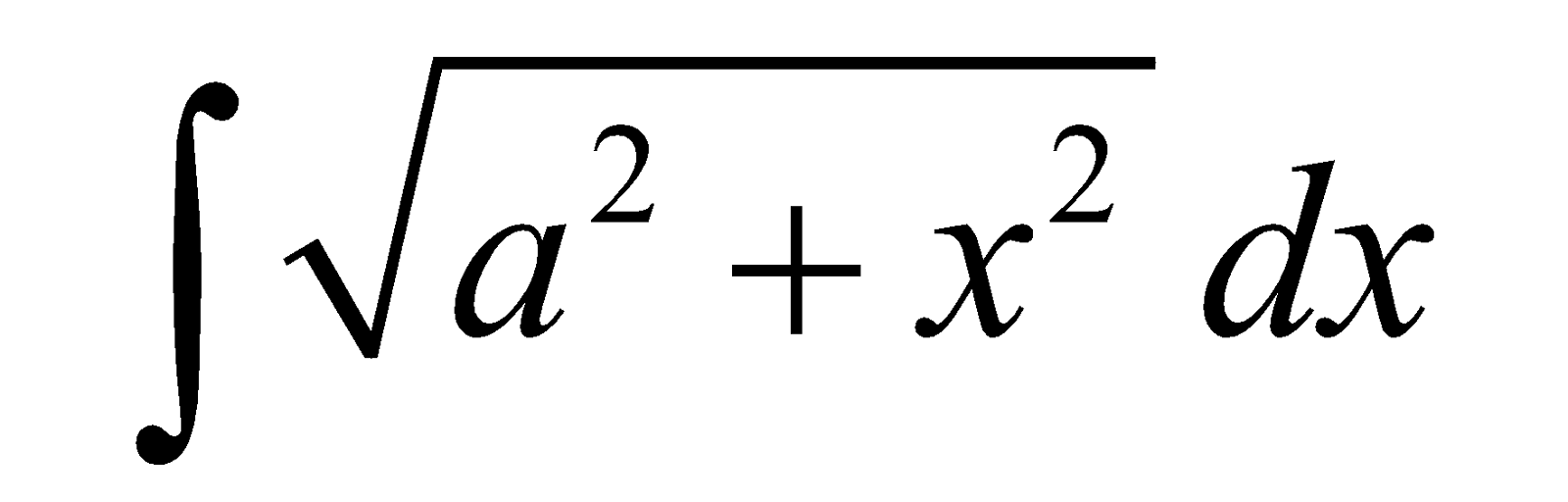

INTEGRATION USING TRIGONOMETRIC IDENTITIES

When the integrand is a trigonometric function, we transform the given function into standard integrals or their algebraic sum by using trigonometric formulae :

The following trigonometric identities are important :

• sin2 mx =
• cos2 mx =
• sin mx = 2 sin cos
• sin3 mx =
• cos3 mx =
• tan2 mx = sec2 mx – 1
• cot2 mx = cosec2 mx – 1
• 2 cos A cos B = cos (A + B) + cos (A – B)
• 2 sin A cos B = sin (A + B) + sin (A – B)
• 2 sin  A sin B = cos (A – B) – cos (A + B)

INTEGRAL OF THE FORM

WORKING PROCEDURE

1. If m is odd. put cos x = t
2. If n is odd. put sin x = t
3. If m and n both odd put sin x = t or cos x = t
4. If m and n both even use trigonometric identities sin2 x =  and cos2 x = or use reduction formula (see next forms)
5. If m and n be rational numbers and is negative integer, put tan x = t.

INTEGRATION OF IRRATIONAL ALGEBRAIC FUNCTIONS

1. If integrand is a function of x and   then substitute (ax + b) = tn.
2. If integrand is a function of x,  and then substitute (ax + b) = tp where p = LCM of m and n.
3. If integrand is a function containing various fractional powers of x, then substitute x = tp where p = LCM of denominators of powers of x.
4. Integrals of the form

where R is a rational function and m1, n1, m2, n2 are integers, can be transformed into an integral of a rational function by substituting ax + b = ts, where s is the least common multiple of the number n1, n2 .......

5. Integrals of the form Put cx + d = t2
6. Integrals of the form   Put px + q = t2
7. Integrals of the formare solved by substituting .
8. Integrals of the form   Put ax + b =
9. Integrals of the form Put x =   followed by c + dt2 = u2

Note : In all of the above forms φ(x) is a rational function of x or constant.

10. Integrals of the form   Put  =
11. Integrals of the form , where m, n and p are rational numbers can be solved as follows :
1. If p is an integer, the integral reduces to the integral of a rational function by means of the substitution x = ts, where s is the least common multiple of the denominator of the fractions m and n.
2. If = s is an integer, the integral can be rationalized by the substitution a + bxn = ts.
3. If +p is an integer, substitute ax–n + b = ts, where s is the denominator of the fraction p.

INTEGRATION BY SUCCESSIVE REDUCTION (REDUCTION FORMULA)

1. Reduction Formula for

Let In =

[Integrating by parts using  as second function]

In =   Where

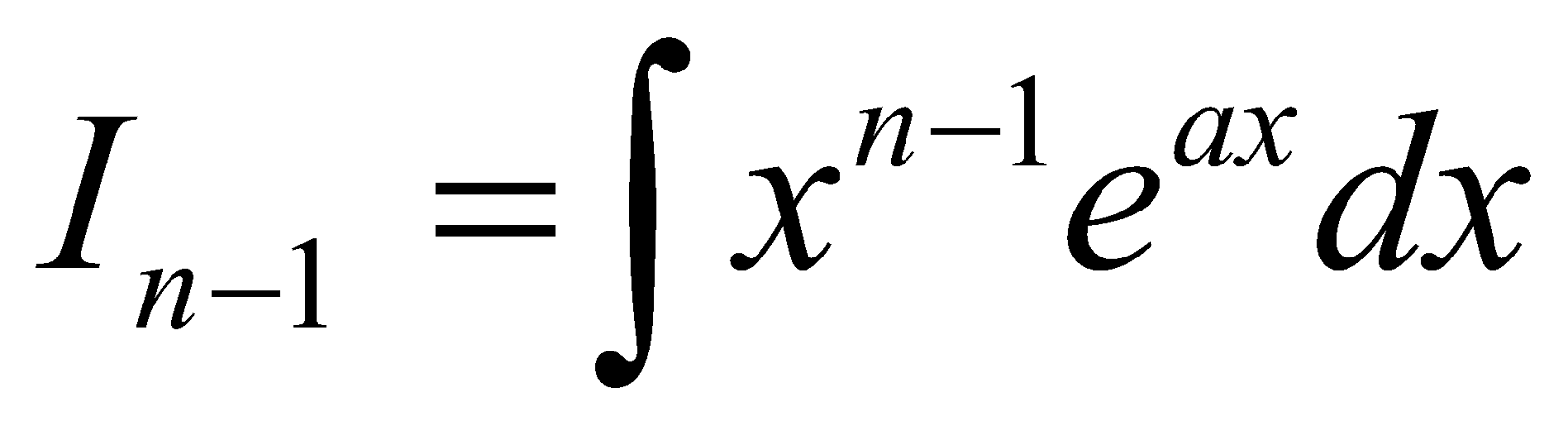
2. Reduction formula for

Let In =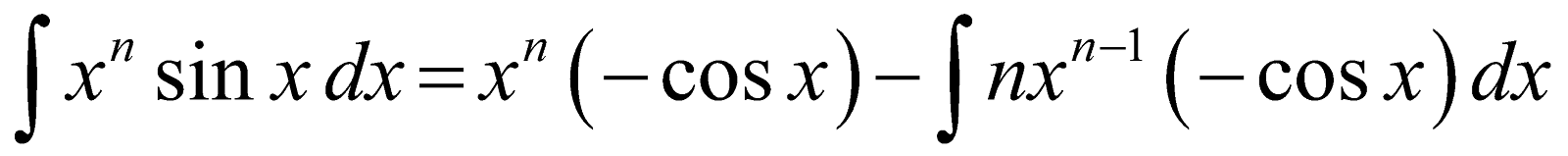

[Integrating by parts using ‘sin x’ as second function]

3. Reduction Formula for

Let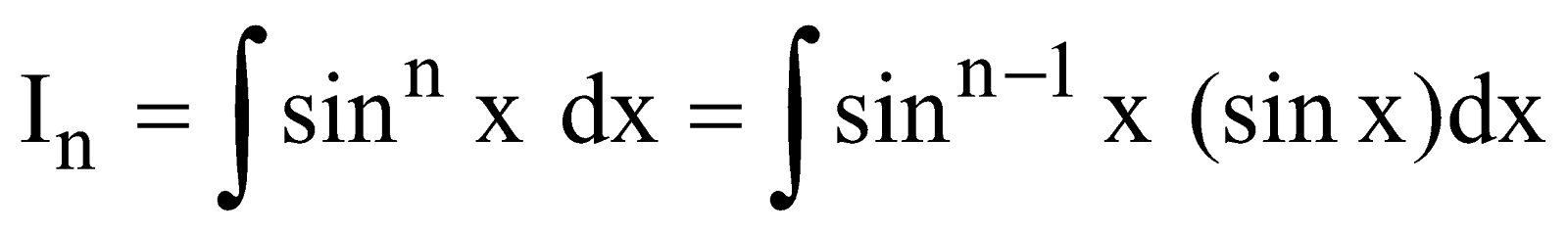

I =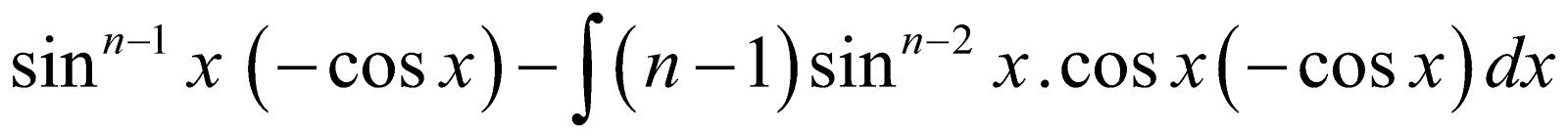

[Integrating by part taking sin x as second function]

4. Reduction Formula for

As for 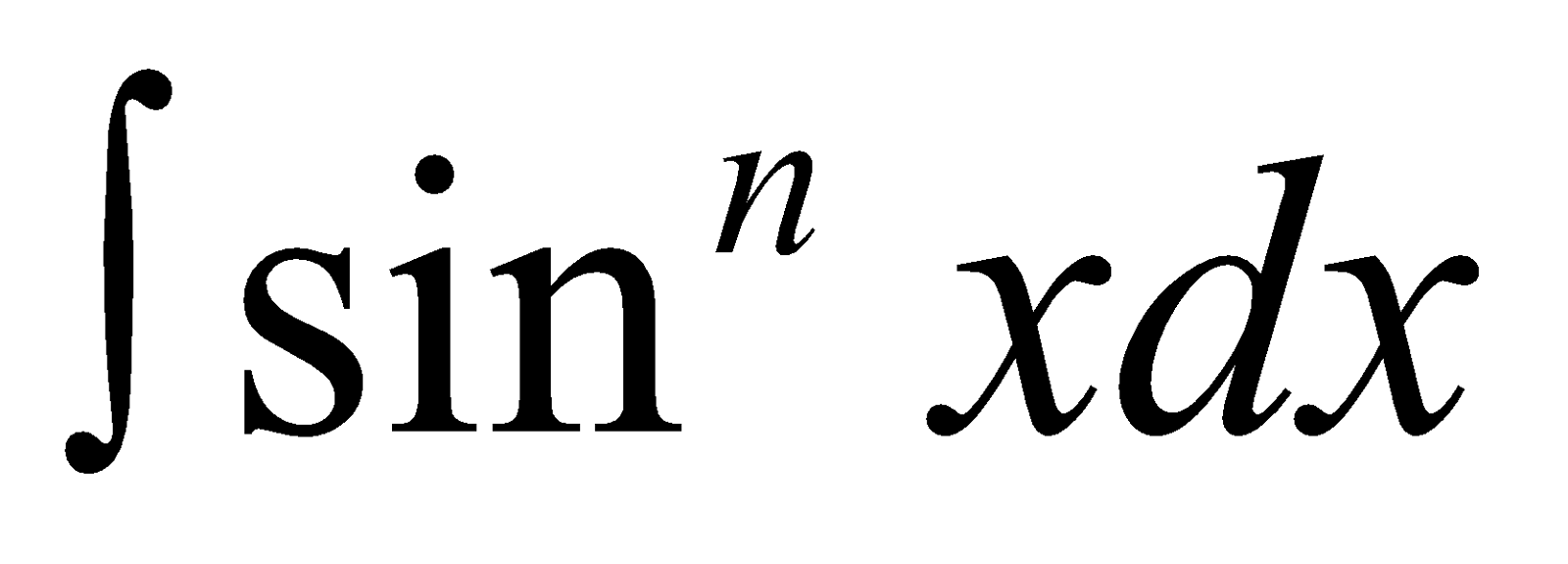, we may find .

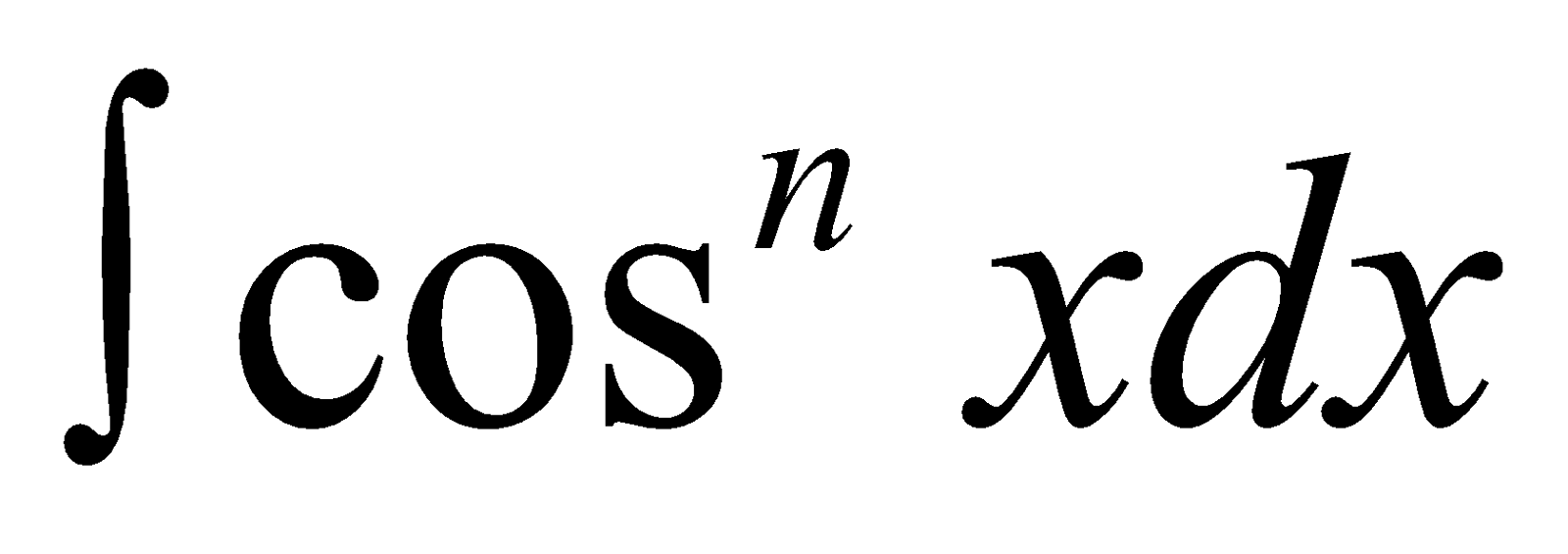The required reduction formula is

5. Reduction formula for

Let In = =

[Put tan x = t]

=

6. Reduction Formula for

As above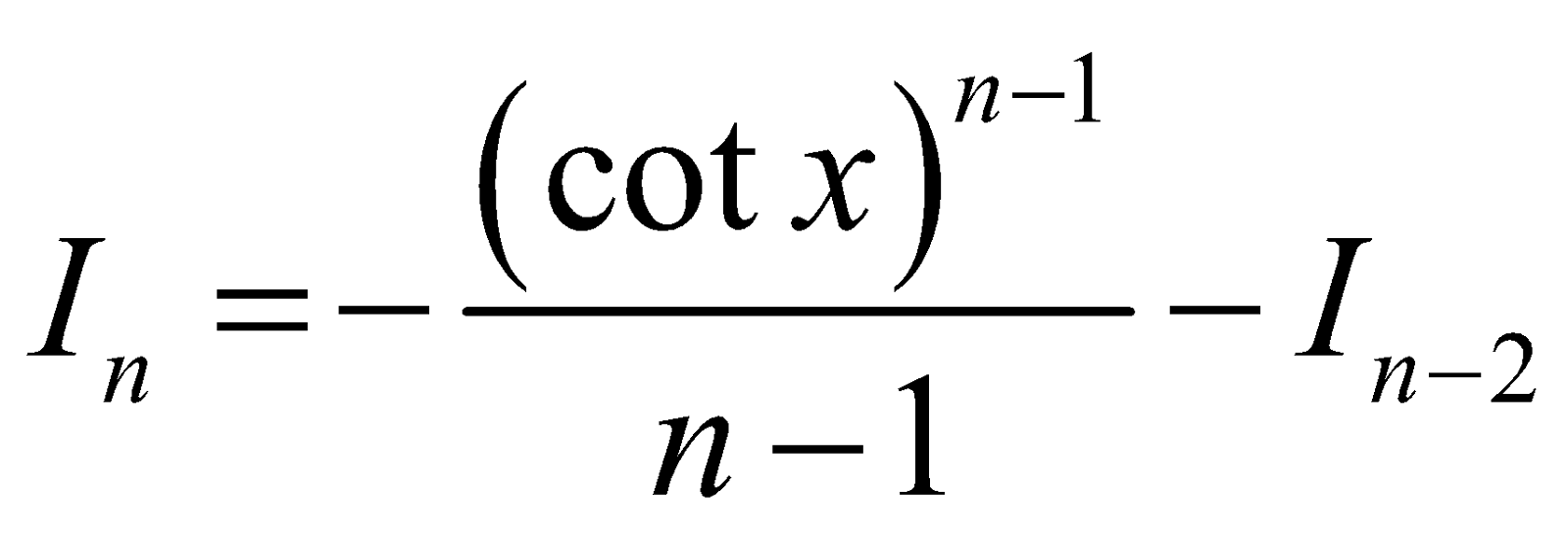

7. Reduction formula for

Let In =

[Integrating by parts taking sec2x as second function]

⇒

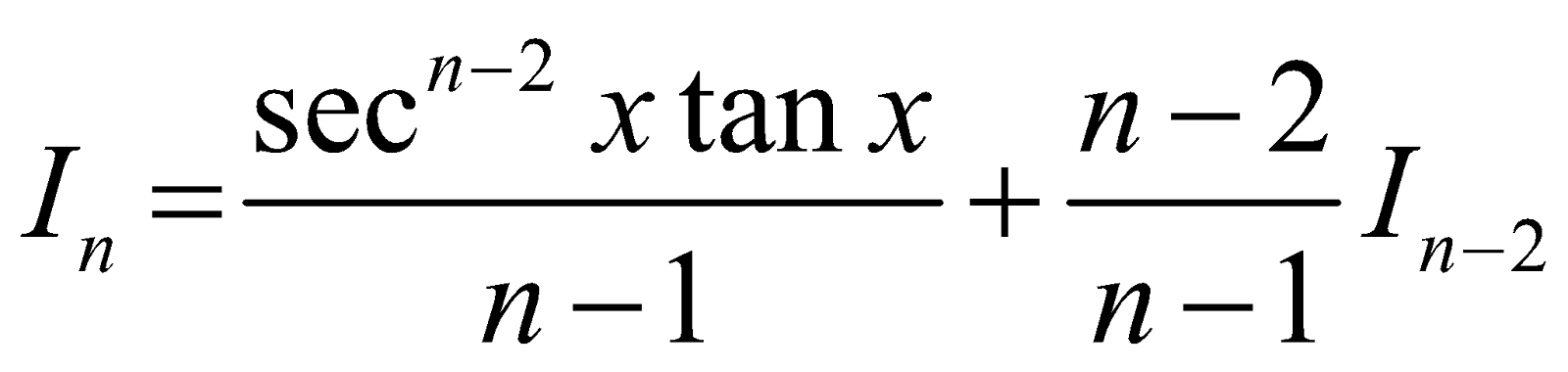
8. Reduction Formula for

As in previous case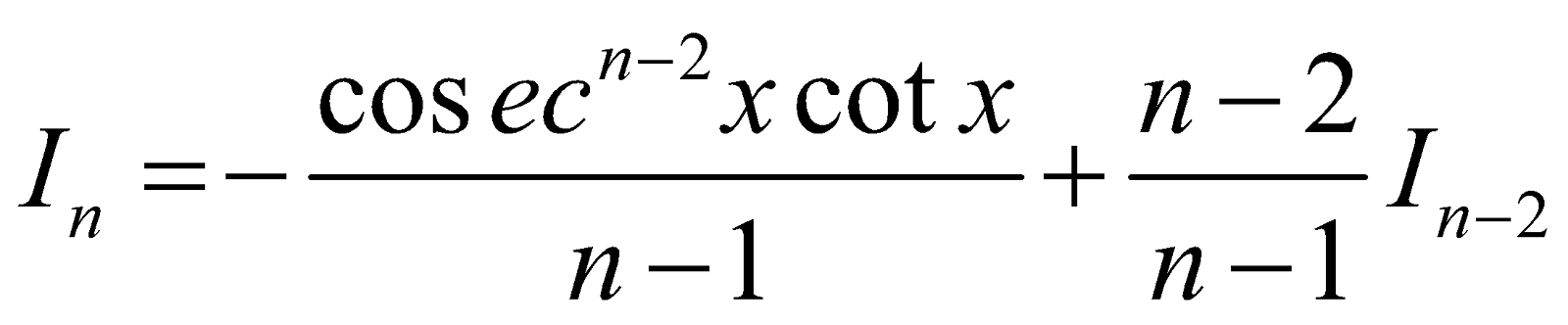

9. Reduction Formula for

Let Im,n =

Integrating by parts using sinmx . cos x as second function

=

=

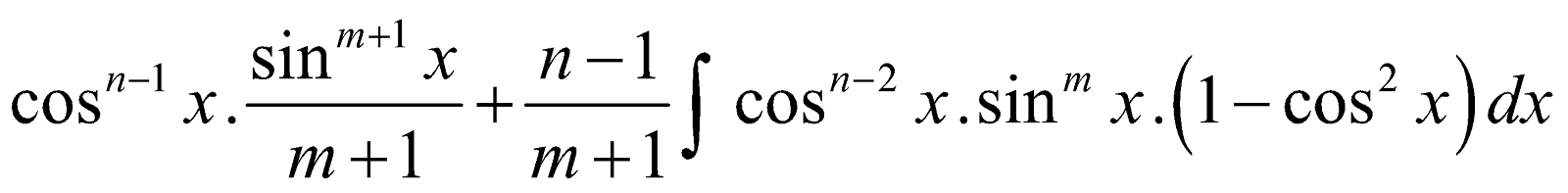
Above reduction formula can also be reduced to the following formula.

These formulae are specifically useful when m and n are both even numbers.

10. Reduction formula for

Let Im,n =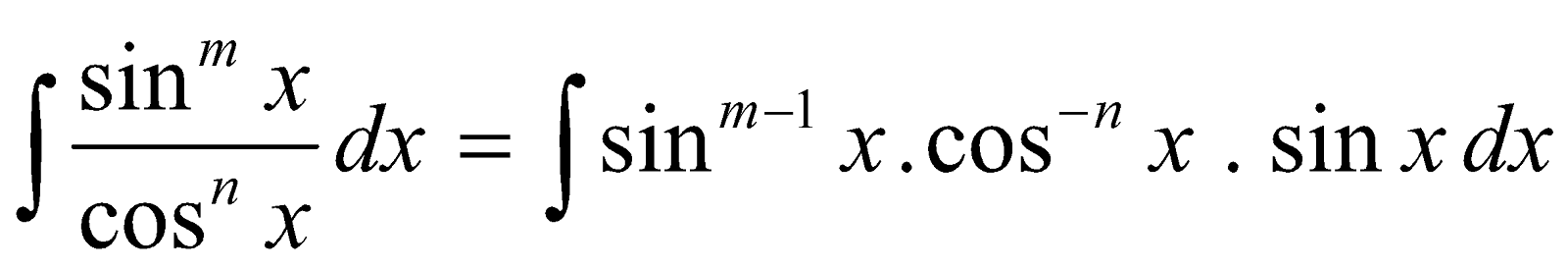

Integrating by parts using as second function

Im,n =

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT