Probability Basic | Mathematics Notes for IITJEE Main

PROBABILITY BASIC

TRIAL AND EVENT

Let us consider an experiment, which does not give unique result but results in any one of the several possible outcomes. Then the experiment is called a TRIAL and the possible outcomes are called EVENTS or CASES. For example,

• Tossing of a coin is a trial and getting head or tail is an event.
• Throwing of a die is a trial and getting, say, 3 is an event.
• Drawing a card from a pack of well-shuffled cards is a trial getting, say, a king is an event.

EXHAUSTIVE NUMBER OF CASES

The total number of possible  outcomes of an experiment in any trial is known as the exhaustive number of events (cases). For example

• In throwing a die, the exhaustive number of cases is 6 since any one of the six faces marked with 1, 2, 3, 4, 5, 6 may come uppermost.
• In tossing a coin, the exhaustive number of cases is 2, since either head or tail may turn over.
• If a pair of dice is thrown, then the exhaustive number of cases is 6 × 6 = 36
• In drawing four cards from a well-shuffled pack of cards, the exhaustive number of cases is 52C4.

MUTUALLY EXCLUSIVE EVENTS

Events are said to be mutually exclusive or incompatible if the occurrence of any one of them prevents or precludes the occurrence of all the others, i.e. if no two or more of them can occur simultaneously in the same trial. for example,

• In tossing of a coin the events head (H) and tail (T) are mutually exclusive.
• In throwing of a die all the six faces are mutually exclusive.
• In throwing of two dice, the events of the face marked 5 appearing on one die and face 5 (or other) appearing on the other are not mutually exclusive.

EQUALLY LIKELY EVENTS

Outcomes of a trial are equally likely if there is no reason for an event to occur in preference to any other event, for example,

• In throwing of an unbiased die, all the six faces are equally likely to occur.
• In drawing a card from a well-shuffled pack of 52 cards, there are 52 equally likely possible outcomes.

FAVOURABLE EVENTS

The favourable cases to an event are the outcomes, which entail the happening of an event, for example,

• In the tossing of a die, the number of cases which are favourable to the “ appearance of a multiple of 3” is  2, viz, 3 and 6.
• In drawing two cards from a pack, the number of cases favourable to "drawing 2 aces” is 4C2.
• In throwing of two dice, the number of cases  favourable to “getting 8 as the sum” is 5, : (2, 6), (6, 2), (4, 4), (3, 5) (5, 3).

INDEPENDENT EVENTS

Events are said to be independent if the happening (or non-happening) of one event is not affected by the happening or non-happening of others

CLASSICAL DEFINITION OF PROBABILITY

If there are n-mutually exclusive, exhaustive and equally likely outcomes to a random experiment and ‘m’ of them are favourable to an event A. then the probability of happening of A is denoted by P (A) and is defined by .

Obviously,  therefore   so that

Since, the number of cases in which the event A will not happen is ‘n – m’, then the probability P () of not happening of A is given by

IMPORTANT POINTS

1. If P (A) = 1, then A is called a SURE EVENT.
2. If P (A) = 0, then A is called an IMPOSSIBLE EVENT.
3. The ODDS IN FAVOUR of occurrence of A are given by m : (n – m), or   P  : P
4. The ODDS AGAINST the occurrence of A are given by (n – m) : m, or P : P (A).

AXIOMATIC APPROACH TO PROBABILITY (SET THEORY APPROACH)

RANDOM EXPERIMENT

The phenomenon where outcomes cannot be precisely predicted are known as random experiments.

For example, tossing a coin, throwing a die, drawing a card from a pack of playing cards, taking out a ball from an urn, etc.

SAMPLE SPACE

The set of all possible outcomes of a random experiment is called the sample space.

Let e1, e2, ......, en be the possible outcomes of a random experiment such that no two or more of them can occur simultaneously and exactly one of them must occur. Then the sample space S = {e1, e2, e3,......en}

For example :

• In tossing of a coin, S = {H, T}
• In rolling a die, S = {1, 2, 3, 4, 5, 6}
• In tossing a coin and rolling a die simultaneously

S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 4), (T, 5), (T, 6)}

EVENT

An event is defined as a subset of the sample space. Single element subset of the sample space, which correspond to each outcome of a random experiment are known as the ELEMENTARY EVENTS or INDECOMPOSABLE EVENTS.

For example :

• In throwing a die, there are six elementary events, viz {1}, {2}, {3}, {4}, {5} {6}.
• In tossing a coin, there are two elementary events {H}, {T}.
• In tossing a pair of coins, there are four elementary events, viz {HH}, {HT}, {TH}, {TT}.

Those subsets of the sample space S related to an experiment which are disjoint union of single element subsets of the sample space S, are known as the DECOMPOSABLE or COMPOUND EVENTS.

For example :

In the experiment of throwing a die, the event of getting an even number is a compound event as it is the union of elementary events {2}, {4}, {6}.

An event represented by a subset ‘E’ of the sample space S related to an experiment is said to have occurred if the outcome ‘w’ of the experiment is such that w∈E.

If the outcome ‘w’ is such that w∉E, we say the event E has not occurred.

Since the set S ⊆ S and every outcome of experiment belongs to S, therefore the event represented by S is a CERTAIN EVENT.

Similarly, the empty set φ is subset of S and no outcome of the experiment belongs to φ . Thus the event represented by φ cannot occur at all when the experiment is performed and is called the IMPOSSIBLE EVENT.

MUTUALLY EXCLUSIVE EVENT

Events represented by subsets E and F of the sample space related to an experiment are mutually exclusive if E∩F = φ.

For example :

In a single throw of die, the following events

A = Getting an even number;

B = Getting an odd number are mutually exclusive.

However the events

A = Getting an even number;

B = Getting a multiple of 3 are not mutually exclusive, because

Let A1, A2, A3,......., An be elementary events related  to an experiment with sample space ‘S’. Then at the same time, if any one of these events occurs the others cannot occur. Therefore, the elementary events are always mutually exclusive.

Also, A1 ∪ A2 ∪ A3 ......∪An = S. Thus, elementary events related to an experiment form a mutually exclusive and exhaustive system of events. i.e.,

(i) Ai ∩ Aj = φ , for i ≠ j, and (ii) A1∪ A2∪..... ∪An = S

FAVOURABLE EVENTS

Those elementary events, which belong to the subset E of the sample space S related to an experiment, are known as favourable events to the event ‘E’.

AXIOMATIC DEFINITION OF PROBABILITY

Suppose the sample space related to a random experiment has ‘n’ elements and let E be a subset of S representing an events ‘A’ If the set ‘E’ consists of ‘m’ elementary events, then the probability of event A is defined as

It follows from the definition that and

The elementary event each has same probability 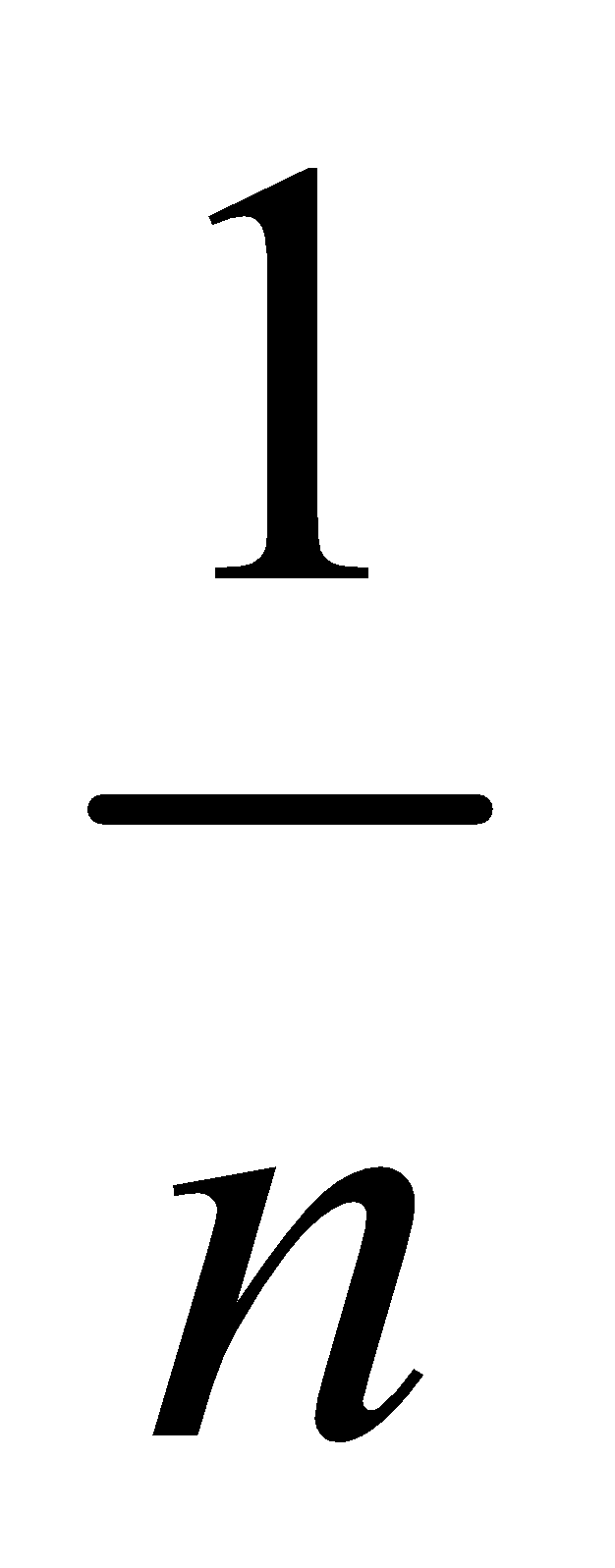. We can also write

ALGEBRA OF EVENTS

Let A and B be two events related to a random experiment. We define

1. The event “A or B” denoted by “AB”, which occurs when A or B or both occur. Thus,

Probability that at least one of the events occur

2. The event “A and B”, denoted by , which occurs when A and B both occur. Thus,= Probability of simultaneous occurrence of A and B.
3. The event “ Not - A” denoted by , which occurs when and only when A does not occur. Thus = Probability of non-occurrence of the event A.
4. denotes the “non-occurrence of both A and B”.
5. “A  B” denotes the “occurrence of A implies the occurrence of B”.

Example :

Consider a single through of die and following two events

A = the number is even = {2, 4, 6}

B = the number is a multiple of 3 = {3, 6}

Then

ADDITION THEOREM ON PROBABILITY

• ADDITION THEOREM : If  A and B are two events associated with a random experiment, then
  
• ADDITION THEOREM FOR THREE EVENTS :  If A, B, C are three events associated with a random experiment, then
  

SOME INTERPRETATIONS

Let  A, B, and C are three arbitrary events, then the events

• Only A occurs
• Both A and B, but no C occur
• All three events occur
• At least one occurs
• At least two occur
• One and no more occur
• None occurs

FINITE PROBABILITY SPACES

Let S be a finite sample space; say, S = {a1, a2, ......an}. A finite probability space is obtained by assigning to each point ai S a real number pi, called the probability of ai, satisfying the following properties:

• Each pi is non negative,
• The sum of the pi is one, p1 + p2 + ........+pn = 1

The probability of an event ‘A’ given by P(A) is then defined to be the sum of the probabilities of the points in A.

Example :

Let three coins be tossed and the number of heads observed; then the sample space is

S = {0, 1, 2, 3}. We obtain a probability space by the following assignment and .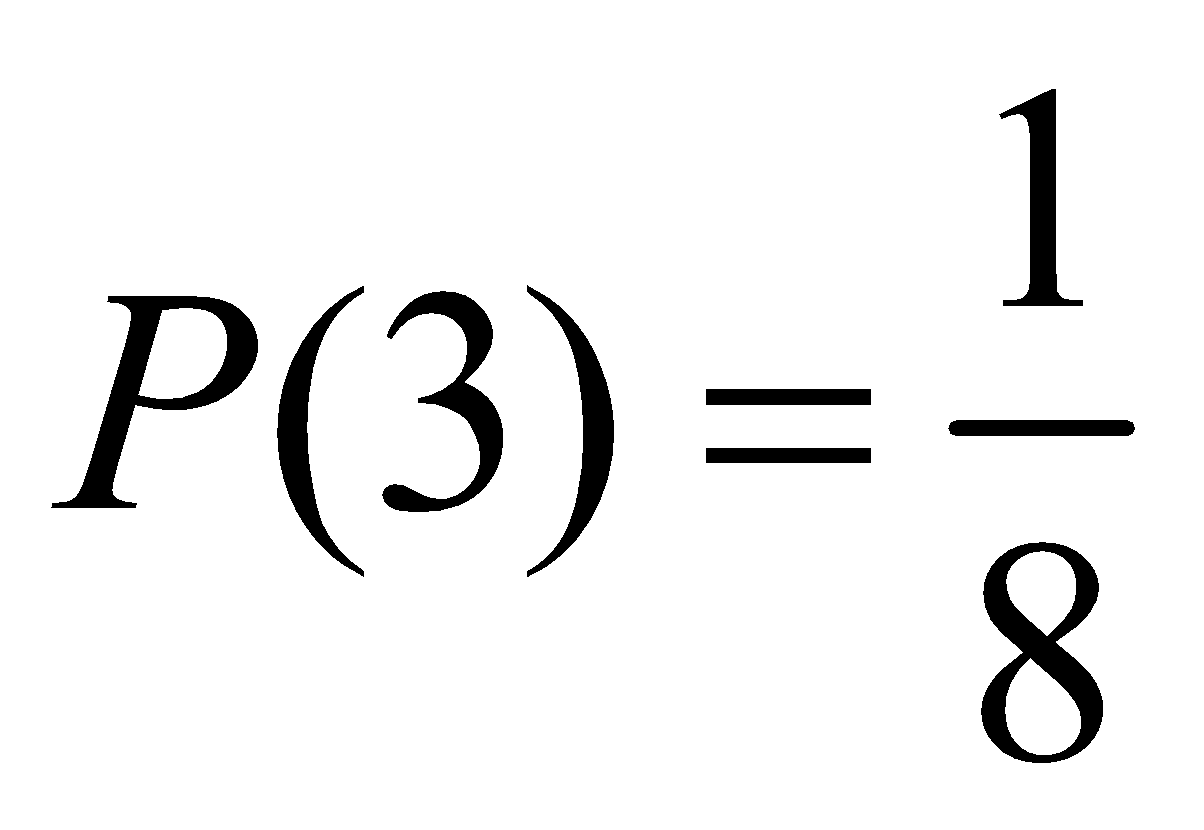

Since each probability is non negative and the sum is 1.

Let A be the event “At least one head appears”.

B be the event “All heads or all tails appear”.

Then A = {1, 2, 3}, and B = {0, 3}

Then by definition

INFINITE SAMPLE SPACE

Suppose S is a countable infinite sample space; say S = {a1, a2, ....}.

As in the finite case, we obtain a probability space by assigning to each ai  S real number pi called its probability, such that

• 
• 

The probability P(A) of any event A is then the sum of the probabilities of its point S.

Example :

Consider the sample space S = {1, 2, 3,.....,  } of the experiment of tossing a coin till a head appears; where ‘n’ denotes the number of times the coin is tossed. A probability space is obtained by setting

 .

UNCOUNTABLE PROBABILITY SPACES

The only uncountable sample spaces S considered (here) are those with some finite geometrical measurement m(S) such as length, area or volume, and in which a point is selected at random. The probability of an event A, i.e., that the selected points belongs to A, is then

or

or

Such a probability space is said to be uniform.

Example :

On the real line R, points a and b are selected at random such that and as shown below. Find the probability ‘p’ that the distance ‘d’ between ‘a’ and ‘b’ is greater than 3.

The sample space ‘S’ consists of the ordered pairs (a, b) and so forms the rectangular region shown in the adjacent diagram. On the other hand, the set A of points (a, b), for which d = a – b > 3 consists of those points of S which lie below the line x – y = 3, and hence forms the shaded area in the diagram.

Thus, the required probability

NOTE:- A finite or countable infinite probability space is said to be discrete, and an uncountable space is said to be non discrete.

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT