DETERMINANTS
DETERMINANTS
A determinant is a particular type of expression written in a special concise form of rows and columns, equal in number.
For example  is a determinant having 2 rows and 2 columns, hence it is of second order. The numbers a1, b1, a2, b2 are called the elements of the determinant.
is a determinant having 2 rows and 2 columns, hence it is of second order. The numbers a1, b1, a2, b2 are called the elements of the determinant.
The value of the above determinant is Δ=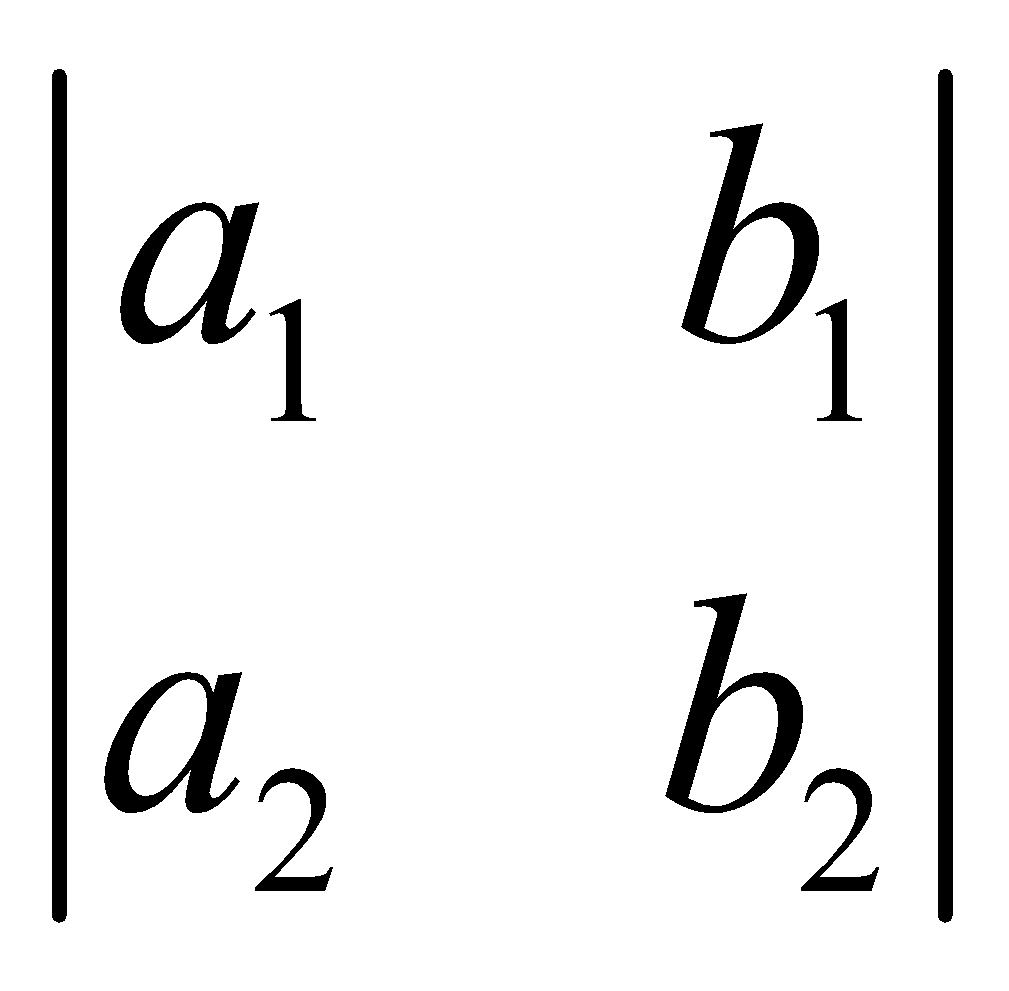 == a1b2 – a2b1.
== a1b2 – a2b1.
Similarly, a determinant of third order is written as
Δ = . It has three rows and three columns. The number of elements = 32 = 9. In general, the number of elements in a determinant of order n is equal to n2.
It has three rows and three columns. The number of elements = 32 = 9. In general, the number of elements in a determinant of order n is equal to n2.
Δ = .
The determinant is expanded along any one row or any one column. The sign to be taken before the elements are  . To expand, take first element of the row (or column) with sign and multiply it with the determinant (of lower order) obtained by omitting the row and the column of the element. For example, let us expand the above determinant along the elements of first row (R1).
. To expand, take first element of the row (or column) with sign and multiply it with the determinant (of lower order) obtained by omitting the row and the column of the element. For example, let us expand the above determinant along the elements of first row (R1).
where,  = cofactor of a1
= cofactor of a1
Putting values of A1, B1, C1
The determinant can be similarly expanded along the elements of some other column (or row), and it can be seen that
Δ = a1A1 + b1B1 + c1C1 = a2A2 + b2B2 + c2C2
= a3A3 + b3B3 + c3C3
= a1A1 + a2A2 + a3A3 = b1B1 + b2B2 + b3B3
= c1C1 + c2C2 + c3C3
Thus there are six ways for expanding a determinant of order 3.
NOTE :
- In a determinant Δ, the determinant (of lower order) obtained by omitting the row and column which contains an element is called the minor of that element in Δ. If the minor is taken with proper sign, then cofactor of that element is obtained. For example, if
Minor of a1 =  , cofactor of a1 = b2c3 – b3c2 = A1
, cofactor of a1 = b2c3 – b3c2 = A1
Minor of b1 =  = a2c3 – a3c2, cofactor of
= a2c3 – a3c2, cofactor of
b1 = – (a2c3 – a3c2) = B1 etc. In general if minor of an element
aij is Mij and its cofactor is Cij then Cij = (–1)i+j Mij
b1 = – (a2c3 – a3c2) = B1 etc. In general if minor of an element
aij is Mij and its cofactor is Cij then Cij = (–1)i+j Mij
- A determinant of nth order can be expanded in successively n! ways.
- It can be shown for the determinant
That
That is expansion by taking elements of a row (or column) and cofactors of other row vanishes.
APPLICATION IN GEOMETRY
- Area of a triangle having vertices (x1, y1), (x2, y2),(x3, y3) can be expressed in determinant form as
- The condition for the equation
representing a pair of straight lines can be written in determinant form as
- The two point form of straight line joining the points A(x1, y1) and B(x2, y2) can be expressed in determinant form as
.
- Three points with coordinates (x1, y1), (x2, y2) and (x3, y3) are collinear if
- Three straight lines having equations a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 and a3x + b3y + c3 = 0 are concurrent if
SARRUS METHOD OF EVALUATION
This method of evaluation of determinants is applicable to determinants of order 3 only. In this method the following diagram is made
The product of three entries on each of three arrows are prefixed by a positive sign and the product of three entries on each of the three dotted lines arrows are prefixed by a negative sign. Thus
PROPERTIES OF DETERMINANTS
Property I : If each entry in any row, or each entry in any column, of a determinant is 0, then the determinant is equal to 0.
For example, 
Property II : The value of a determinant is not altered by changing its columns into rows and rows into columns. Thus,
Property III : If two adjacent rows or columns of a determinant are interchanged, the sign of the determinant is changed, but its numerical value is unaltered. Thus, if
Where Δ' is obtained by interchanging the first and second columns (C1 and C2), then 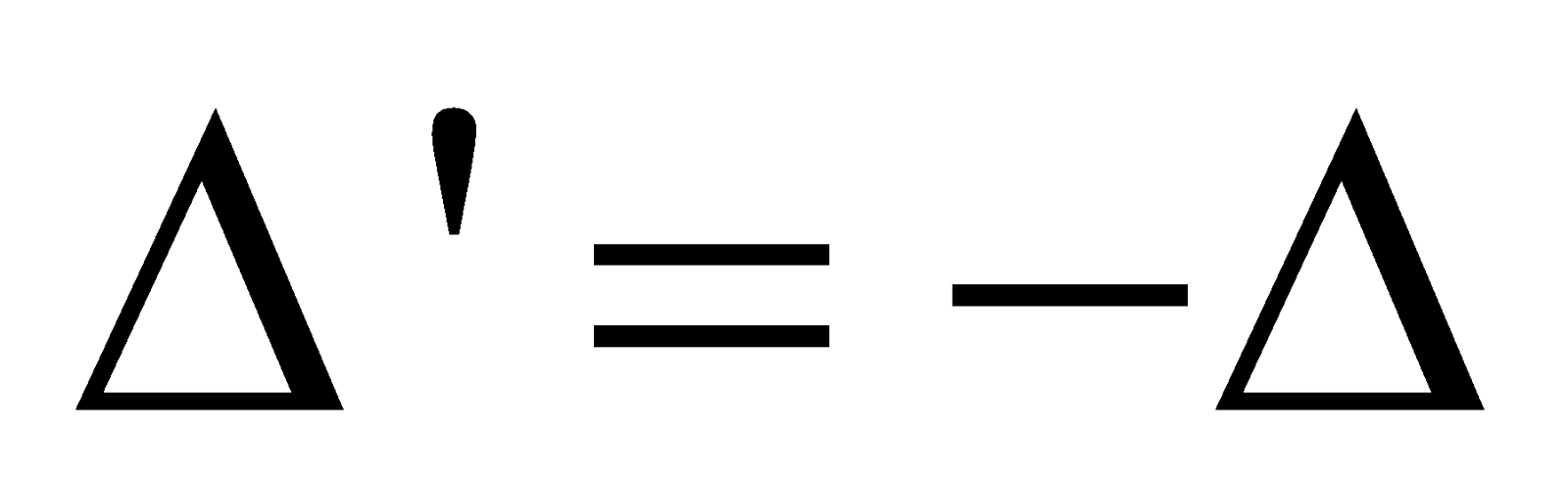 .
.
If any row (or a column) of a determinant is passed over m parallel rows (or columns), the resulting determinant 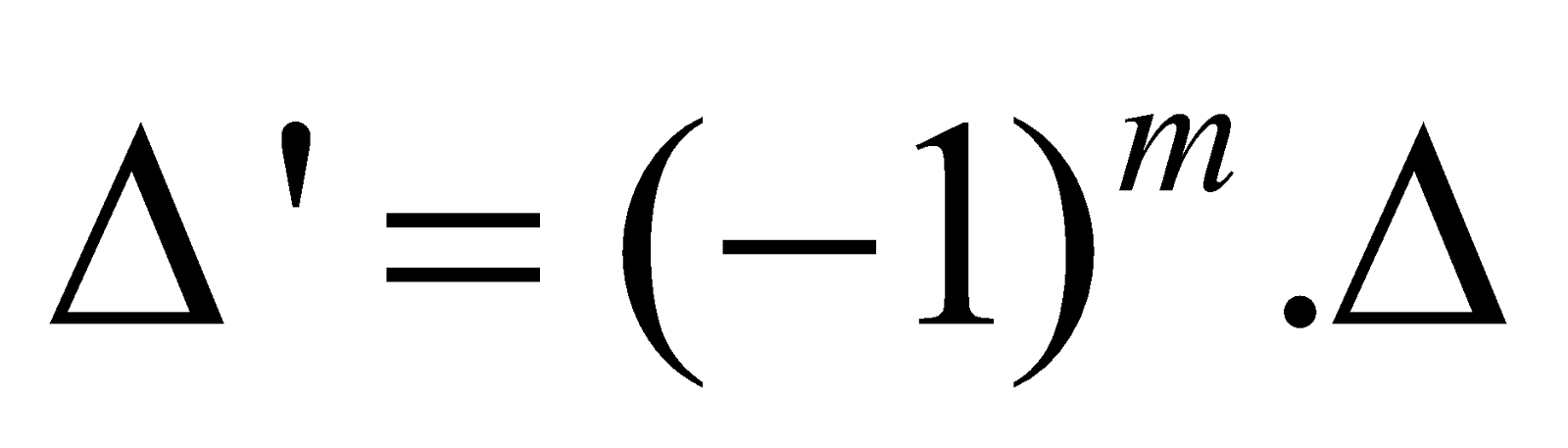
Property IV : If two rows or columns of a determinant are identical, the value of the determinant is zero. Thus,
If the element in a row (or column) of a determinant are respectively equal to k times the corresponding elements in another row (or column), the value of the determinant is zero.
Property V : If every element in a row, or a column, of a determinant is multiplied by the same constant, then the value of the determinant gets multiplied by that constant.,
Let Δ =  .
.
Then Δ' = kΔ
Property VI : If each element of any row or any column of a determinant can be expressed as a sum of two terms then the determinant can be expressed as the sum of the two determinants. Thus
Property VII : If to the elements of a row (or a column) of a determinant, same multiples of the corresponding elements of any other row (or column) of the same determinant are added (or subtracted), the value of determinant is not altered. This is a very useful property used in the evaluation of determinants.
For example, let
Δ =  . Then Δ' = Δ.
. Then Δ' = Δ.
Property VIII : If to each element of a row (or column) of a determinant be added, the equimultiples of the corresponding elements of one or more parallel rows (or columns), the determinant remain unaltered.
Let  . Then Δ' = Δ.
. Then Δ' = Δ.
Property IX : If on putting x = α, the determinant vanishes, then (x – α) is factor of the determinant. For example, if
then x – 2 is a factor of the determinant since on putting
x = 2, C1 and C2 become identical which made Δ = 0. Thus by factor theorem (x – 2) is a factor of the determinant.
x = 2, C1 and C2 become identical which made Δ = 0. Thus by factor theorem (x – 2) is a factor of the determinant.
MULTIPLICATION OF TWO DETERMINANTS
MULTIPLICATION OF SECOND ORDER DETERMINANTS
The product of two determinants of second order is also a determinant of second order.
Let 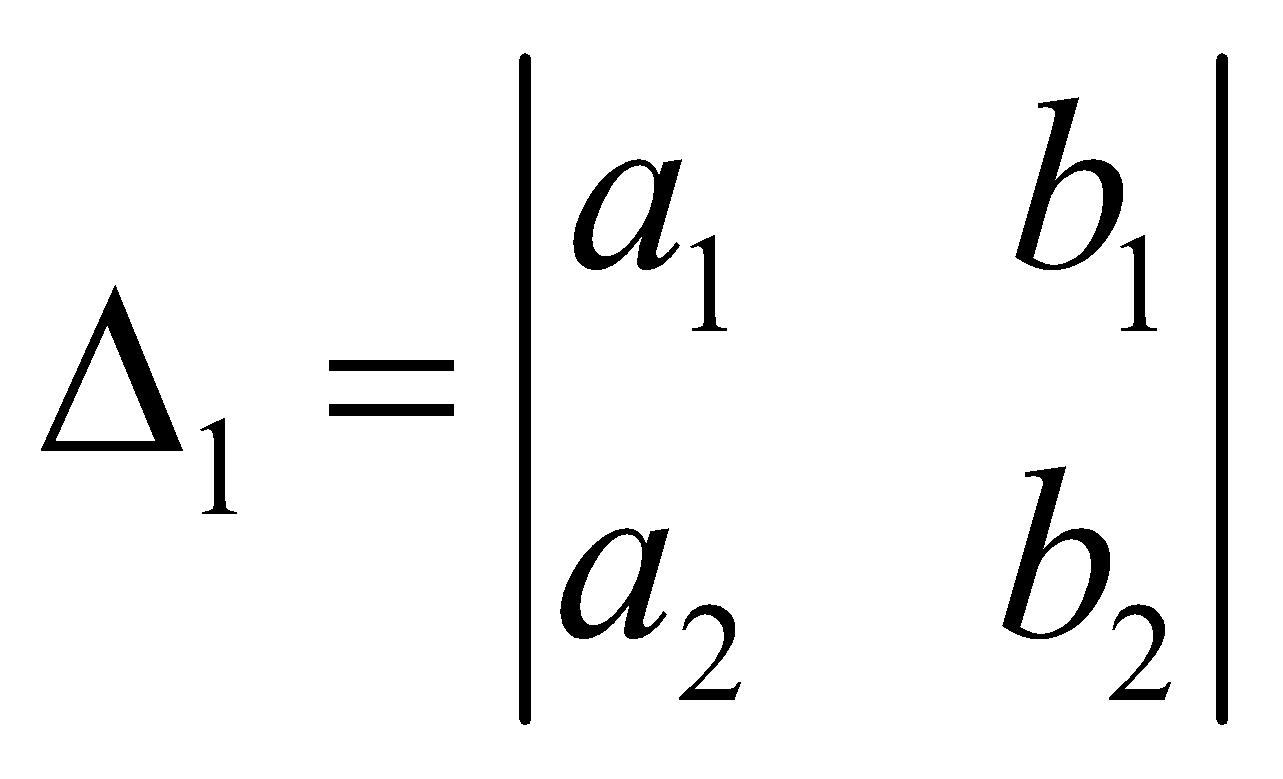 and
and
Then 
Here note that ith row jth column element (pij) of product determinant is obtained by multiplying the elements of ith row of first determinant (Δ1) by the corresponding elements of jth column of the second determinant (Δ2), and then adding them.
MULTIPLICATION OF THIRD ORDER DETERMINANTS
Let 
Then
The elements of product determinant Δ are obtained in the same manner as for the product determinant of second order i.e.,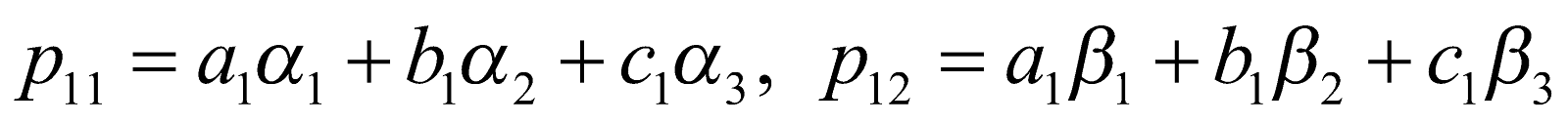 etc.
etc.
IMPORTANT POINTS
- The above is row by column multiplication rule since the value of the determinant is not altered by interchanging rows and columns, we can also follow row by row rule or column by row rule or column by column rule, for example Δ1Δ2 can be expressed as following also :
[Row by Row multiplication]
- Multiplication of two nth order determinants is also a determinant of nth order.
For Example
Let  and
and 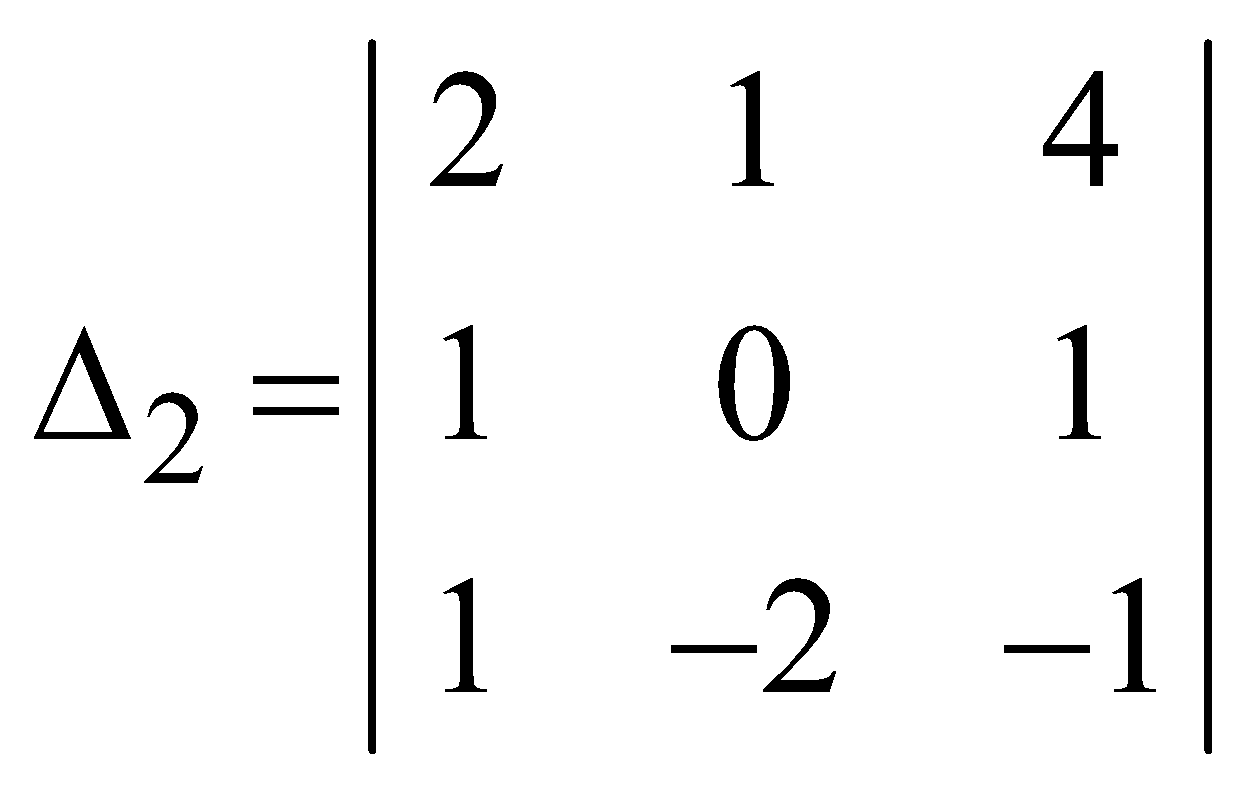
be two third order determinants then
Above is obtained using column by column multiplication. Again using row by row multiplication, we get
Further using row by column multiplication, we get
Similarly we can find Δ1Δ2 using column by row multiplication we see that the entries of the determinant Δ1Δ2 obtained by different method are different but the value comes out to be – 10 on expanding any of the forms. Also, Δ1 = 5 and Δ2 = – 2. Thus Δ1Δ2 = – 10.
THEOREM
If the determinant Δ' is obtained by replacing the elements of nth order determinant Δ by their corresponding cofactors, then Δ' = Δn–1. Thus for third order determinant Δ' = Δ2.
Proof : Let
Where the capital letters denote the cofactors of the corresponding elements with small letters in Δ. By row to row multiplication rule,
Here a1A1 + b1B1 + c1C1 = Δ etc. and a1A2 + b1B2 + c1C2 = 0
Thus ΔΔ' = 
The determinant Δ' is called the reciprocal determinant of Δ.
DIFFERENTIATION OF A DETERMINANT
SECOND ORDER DETERMINANT
Let 
Then, 
If we write  where Ci denotes the ith column, then
where Ci denotes the ith column, then 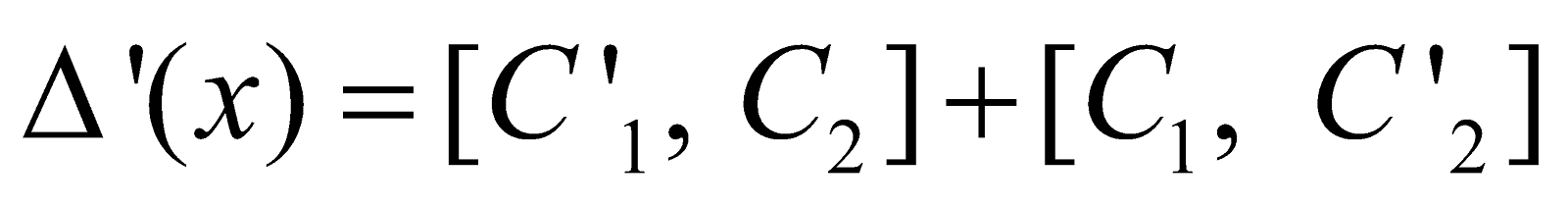
Where C' denotes that column with contains the derivative of all the functions in the ith column Ci, i = 1, 2.
Further if we write . Then
. Then 
THIRD ORDER DETERMINANT
Next if  and if we write
and if we write 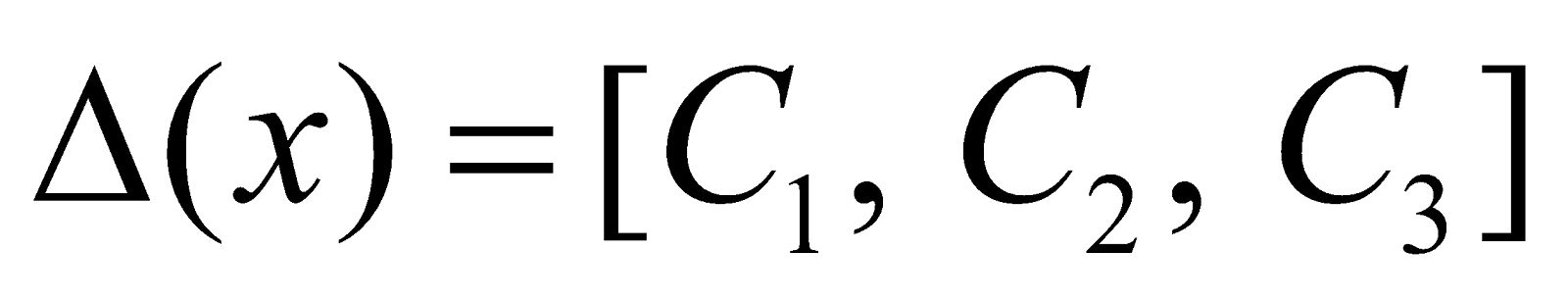 then
then
Again if we write 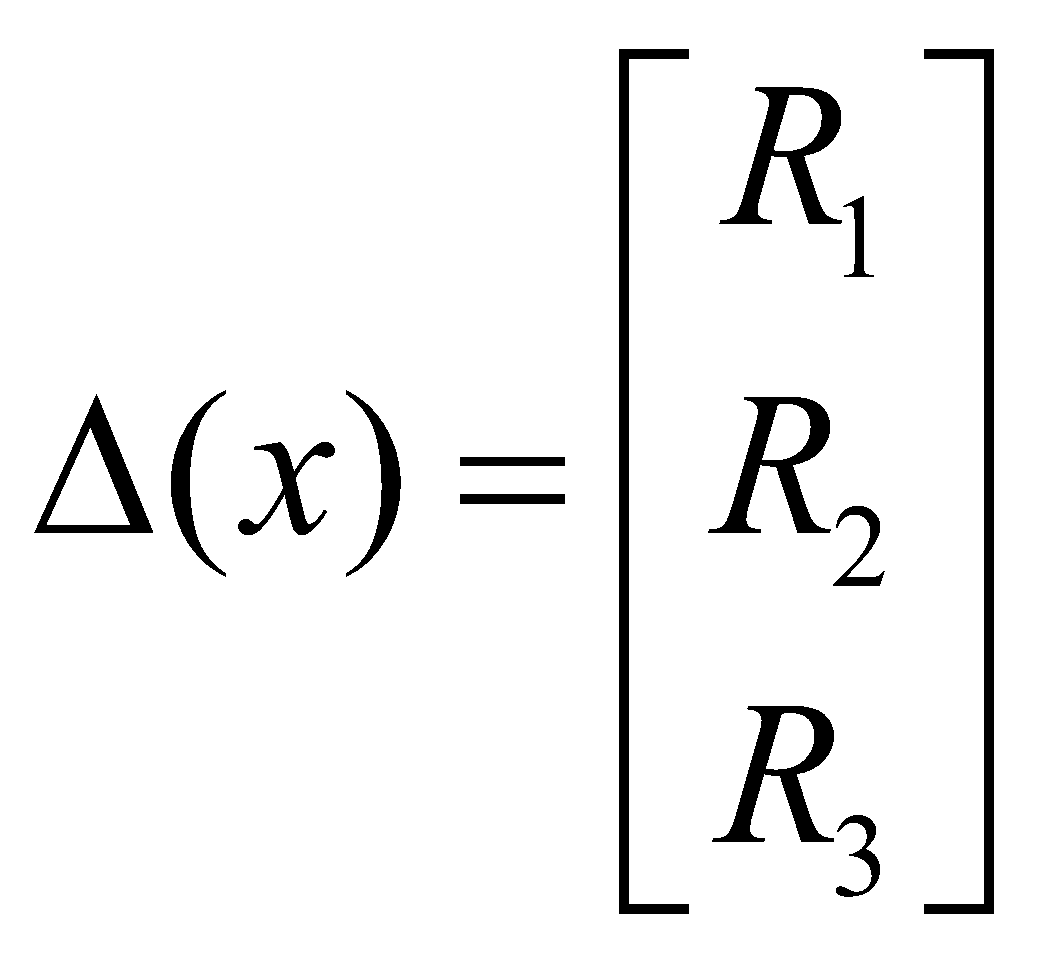 . Then
. Then 
For Example :
Let 
then 


[Differentiating along Rows]
Again
[Differentiating along columns]
SOLUTION OF SYSTEM OF LINEAR EQUATIONS USING DETERMINANT METHOD (CRAMER'S RULE)
SYSTEM OF EQUATIONS IN TWO VARIABLES
Consider the simultaneous equations a1x + b1y = c1, a2x + b2y = c2
Solving these equations,
we get x = , y =
, y = 
Writing determinants, we can express the solution as ,
Where the determinant Δ in the denominator is the determinant of the coefficients. In the determinant Δx, the coefficient of x, i.e. a1 and a2 are replaced by the constant terms c1 and c2, while in the determinant Δy, the coefficients of y, i.e., b1 and b2 are replaced by the constant terms.
CONSISTENT, INCONSISTENT AND DEPENDENT EQUATIONS
- A system of equations is said to be consistent if its solution exists, otherwise it is said to be inconsistent.
- If a system of equations has a unique solution, then it is said to be consistent and determinate.
For example, the system of equation x + y = –1; 8x + 3y = 2; has unique solution x = 1, y = –2, hence the system is consistent and determinate.
- If a system of equations has infinite number of solution, then it is said to be consistent and indeterminate(or dependent).
For example the system of equations x + y = 5; 4x + 4y = 20 has infinitely many solutions given by x = k, y = 5 – k, k is any real number. Hence, it is consistent but indeterminate system. The system of equations x + y = 5, 4x + 4y = 7 has no solution, hence it is an INCONSISTENT SYSTEM.
CONSISTENCY AND INCONSISTENCY OF SIMULTANEOUS LINEAR EQUATIONS WITH TWO VARIABLES
- If Δ ≠ 0, then the given system of equations is consistent and has a unique solution, namely,
- If Δ = 0 and Δx = Δy = 0, then the system may be consistent with infinitely many solutions or inconsistent.
- If Δ = 0 and at least one of Δx and Δy is non-zero then the system has no solution, i.e., the system is inconsistent.
SYSTEM OF EQUATIONS IN THREE VARIABLES
Consider the following system of equations
then 
[Substituting for d1, d2, d3 from (1)]
= 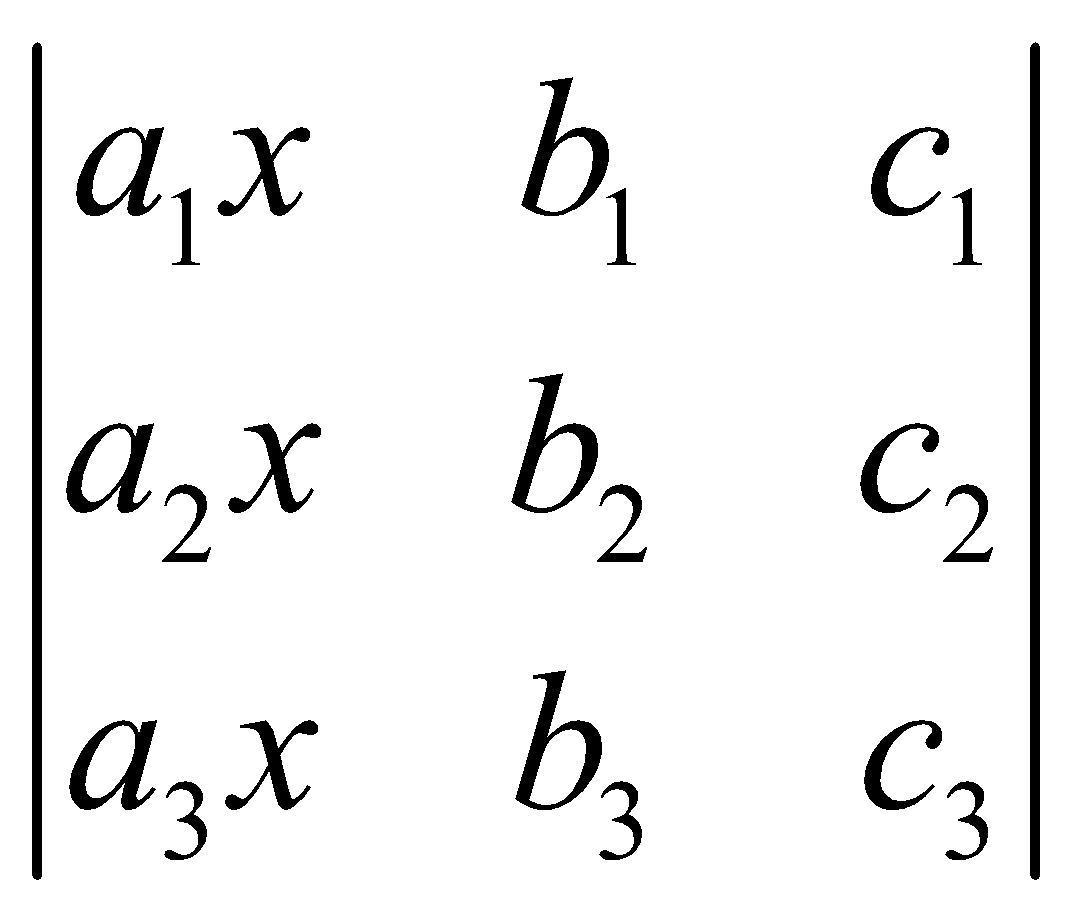 (Since the other two determinants out of three into which the determinant on the right side is split up, vanish).
(Since the other two determinants out of three into which the determinant on the right side is split up, vanish).
= 
Similarly,
CONSISTENCY AND INCONSISTENCY OF SIMULTANEOUS LINEAR EQUATIONS WITH THREE UNKNOWNS
- If Δ ≠ 0, then the given system of equations is consistent and has a unique solution, namely,
- If Δ = 0 and Δx = Δy = Δz = 0, then the given system may be consistent with infinitely many solutions in which case take any two equations out of the three given equations and shift one of the variables say z on the right hand side to obtain two equations in x, y. Solve these two equations by Cramer's rule to obtain x, y in terms of z.
If Δ = 0 and Δx = Δy = Δz = 0, the system may or may not be consistent, as in that case the value of x, y, z assume an indeterminate form.
- If Δ = 0 and at least one of the determinants Δx, Δy, Δz is not zero, then the given system of equations is inconsistent. The Cramer's rule may be extended to solve the simultaneous linear equations in any number of variables.
SYSTEM OF HOMOGENEOUS LINEAR EQUATIONS
If d1 = d2 = d3 = 0 in the set of equations (1) discussed in previous article, then the system is called a homogeneous system of equations. Thus, a homogeneous system of equations is
Clearly, Δx = Δy = Δz= 0
Hence, if then the solution of the equations is x = y = z = 0. It is called TRIVIAL SOLUTION.
If Δ = 0, then the system of equations has infinitely many solutions. (Since, Δ = Δx = Δy = Δz = 0).
It is called NON-TRIVIAL SOLUTION.
A homogeneous system of linear equations is always consistent.







