Trigonometric Ratios and Identities | Mathematics Notes for IITJEE Main

TRIGONOMETRIC RATIOS AND IDENTITIES

ANGLES

An angle is formed by the rotation of a ray in a plane, around the end point called the VERTEX. The original position of the ray is called the INITIAL SIDE

The final position of the ray after rotation is called the TERMINAL SIDE of the angle

The revolving ray is called the GENERATING LINE of the angle.

By convention, an angle is considered positive if it is generated by counter-clockwise motion of the revolving ray and the angle is regarded as negative if the motion is in clockwise direction.

The angle between two perpendicular lines is called a RIGHT ANGLE.

MEASUREMENT OF ANGLES

There are three principal system for measuring angles.

SEXAGESIMAL OR DEGREE SYSTEM (ENGLISH SYSTEM)

A right angle is divided into 90 equal parts. Each part is said to be one degree (1°). A degree is divided into 60 equal parts and each part is called a minute (1’). A minute is again divided into 60 equal parts and each part is called a second (1”). Thus 1 right angle = 90 degrees (90°)

1° = 60 minutes (60’)

1’ = 60 seconds (60”)

CENTESIMAL SYSTEM OR GRADE SYSTEM (FRENCH SYSTEM)

A right angle is divided into 100 equal parts Each part is said to be 1 grade (1g). Each grade is divided into 100 equal parts called a minute 1'. Each minute is divided into 100 equal parts called a second 1"

Note that minutes and seconds of sexagesimal system are not the same as the centesimal minutes and seconds.

CIRCULAR SYSTEM OR RADIAN SYSTEM

We know that for any circle, other than a point circle, the ratio of the circumference to its diameter is always constant. This constant is an irrational number denoted by π, whose value is 3.1415926536  [approximately , correct upto 2 decimal places] Hence,

We define a RADIAN (1c) as the measure of an angle at the centre of a circle subtended by an arc equal in length to the radius of the circle.

For a general angle,

Thus, if in a circle of radius r, an arc of length l subtends an angle θ radians at the centre, then .

Clearly, one complete revolution of initial side traverses an angle of   radians.

In general the angle θ radian is symbolically denoted by θc But the system is so frequently used that we omit the symbol (c) and the angle θ  is always understood to be θ  radian.

RELATION BETWEEN THREE SYSTEMS

Let D be the number of degrees, G the number of grades and C the number of radians of an angle AOB. For one complete rotation the angle subtended is 360° and 2π radian.

Also, 1 radian =  = 57° 17’ 45’’ (approx)

We therefore get       ....(i)

Similarly, 100 grades = 1 rt. angle = 90°

.  We have therefore     ....(ii)

From (i) and (ii),  .

IMPORTANT NOTE

1. The sum of interior angles of a polygon of n-sides = (n – 2) × 180º = (n – 2) π
2. Each interior angle of a REGULAR polygon of n-sides =
3. The sum of exterior angles of a polygon of any number of sides = 360º = 2π

TRIGONOMETRIC FUNCTIONS OR TRIGONOMETRIC RATIOS (T-RATIOS)

Suppose that in a right angled triangle ABC, ∠BAC = θ.
We define the following trigonometric ratios for the angle θ.

DOMAIN AND RANGE OF TRIGONOMETRIC FUNCTIONS

The sin θ function is defined for all real values of  θ. Hence the domain of sin θ is set of real numbers R.

Further for any value of θ, sin θ can take value between –1 and 1 only, including –1 and 1, i.e., –1 ≤ sin θ ≤ 1. Hence, the range of values of sin θ is [–1, 1].

Following table provides the range and domain for all trigonometric functions.

BASIC FORMULAE OF TRIGONOMETRIC FUNCTIONS

1. sin θ . cosec θ = 1 or
2. cosθ . sec θ = 1

or   

3. tan θ . cot θ = 1 or
4. 
5. 
6. 
7. 
8. 

SIGN OF TRIGONOMETRIC FUNCTIONS

Two perpendicular lines intersecting at a point O divide a plane in 4 right angles, each is called a quadrant. If θ be the angle that a line OA subtends with the initial line OX, anticlockwise then.

In I Quadrant, 0° < θ < 90°

In II Quadrant, 90° < θ < 180°

In III Quadrant, 180° < θ < 270°

In IV Quadrant, 270° < θ < 360°

The following table illustrates the sign of various trigonometric functions in all the four quadrants

I II III IV

sin θ + + – –

cos θ + – – +

tan θ + – + –

cot θ + – + –

sec θ + – – +

cosec θ + + – –

More precisely, we can discuss the way of increase and decrease of trigonometric functions as described in the following tables :

PERIODIC FUNCTIONS

A function f is said to be periodic if there exists a real number
T > 0 such that f (x + T) = f (x) for all x. T is called the period of the function.

All trigonometric functions are periodic functions with following periods.

For sin θ, cos θ, sec θ, and cosec θ, the period = 2π. For
tan θ and cot θ the period = π

THEOREM : If f(x) is a periodic function with period T, then f (ax + b) is a periodic function with period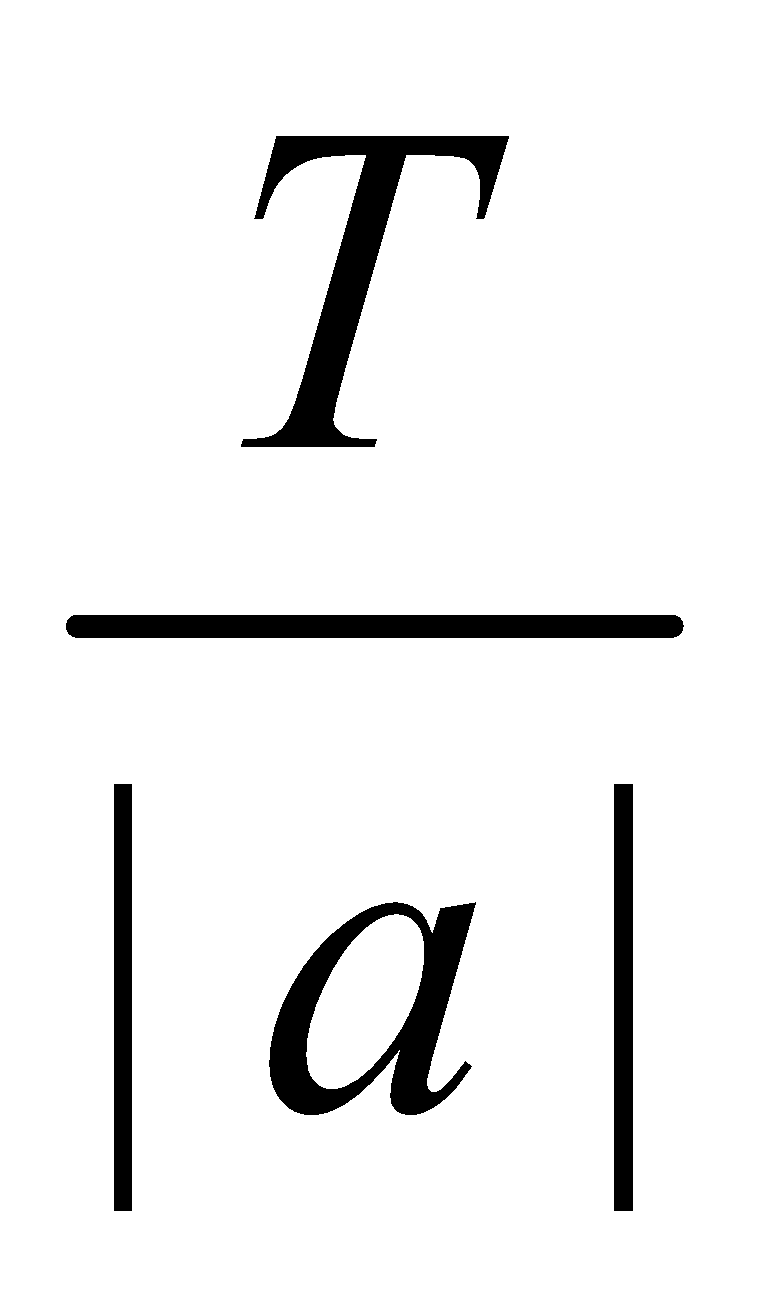

For example :

Period of sin θ is 2π
Period of sin 2θ is

Period of  

Period of 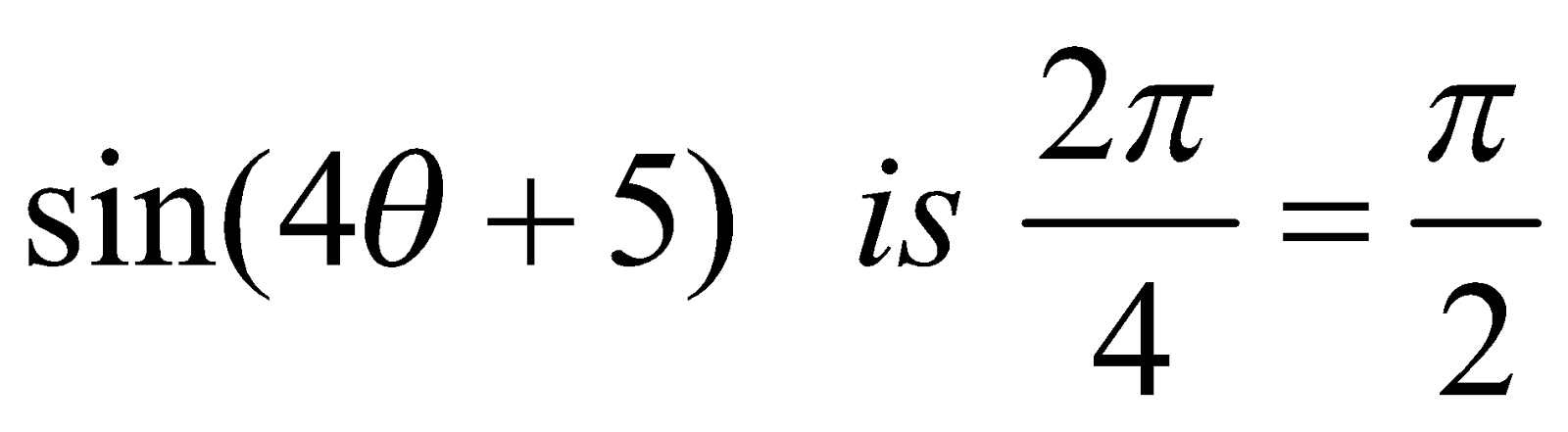....... etc.

PERIOD OF SOME IMPORTANT TRIGONOMETRIC FUNCTIONS

1. Periods of sinnθ, cosnθ, secnθ, and cosecn θ = 2π if n is odd and π if n is even
2. Periods of tannθ,cotnθ, = π, n even or odd.
3. Periods of  |sinθ|, |cosθ|, |tanθ|, |cot θ|, |secθ|, |cosec θ|= π
4. Periods of   |sin θ| + |cos θ|, |tan θ| + |cot θ|, |sec θ| + |cosec θ| are

TRIGONOMETRIC RATIOS OF COMPOUND ANGLES

• Conversion Table for T-Ratios of  –θ in terms of T-Ratios of θ.

sin (– θ) = – sin θ, cos (– θ) = cos θ,

tan (– θ) = – tan θ cot (– θ) = – cot θ,

sec (– θ) = sec θ, cosec (– θ) = – cosec θ

• Conversion Table for T-Ratios of in terms of T-Ratios of θ

       

   

   

• Conversion Table for T-Ratios π ± θ in terms of T-Ratios of θ

sin (π − θ) = sin θ sin (π + θ) = − sin θ

cos (π − θ) = – cos θ cos (π + θ) = − cos θ

tan (π − θ) = – tan θ tan (π + θ) =  tan θ

cot (π − θ) = – cot θ cot (π + θ) = cot θ

sec (π − θ) = – sec θ sec (π + θ) = − sec θ

cosec (π − θ) = cosec θ cosec (π + θ) = − cosec θ

• Conversion Table for T-Ratios of in terms of T-Ratios of θ.

 

• Conversion Table for T-Ratios of  2π ± θ in terms of T-Ratios of θ.

               

                 

              

                  

                      

   

We can write the results of allied angles in case of sin, cos and tan in a generalised form as following :

1. sin nπ = 0
2. cos nπ = (–1)n
3. tan nπ = 0
4. sin (nπ + θ) = (–1)n sin θ
5. cos (nπ + θ) = (–1)n cos θ
6. tan (nπ + θ) = tan θ
7. sin  =  cos θ, where n is odd
8. cos =  sin θ, where n is odd
9. tan  = –cot θ, where n is odd

To find ratios for nπ – θ and , replace θ by –θ in all of the above.

TRIGONOMETRIC RATIOS OF SUM AND DIFFERENCE OF ANGLES

1. 
2. 
3. 
4. 
5. ,
6. 
7. ,
8. 
9. 
10. 

Generalisation :

1. sin (A1 + A2 + ...... + An) = cos A1 cos A2 ...... cos An (S1 – S3 + S5 – ....)
2. cos (A1 + A2 + ...... + An) = cos A1 cos A2 ...... cos An (1 – S2 + S4 – S6 + ....)
3. tan (A1 + A2 + ...... + An) =

where S1 = Σ tan A , S2 = Σ tan A1 tan A2,

          S3 = Σ tan A1 tan A2 tan A3 and so on.

FORMULAS TO TRANSFORM PRODUCTS INTO SUM AND DIFFERENCE

1. 2 sin A cos B = sin(A+B) + sin (A – B)
2. 2 cos A sin B = sin (A+B) – sin (A – B)
3. 2 cos A cos B = cos (A+B) + cos (A – B)
4. 2 sin A sin B = cos (A – B) – cos (A + B)

FORMULAS TO TRANSFORM SUM OR DIFFERENCE INTO PRODUCT

1. 
2. 
3. 
4. 

TRIGONOMETRIC FUNCTIONS OF MULTIPLE AND SUB-MULTIPLE ANGLES

1. ;

2. 

3. ;  
4. ;  
5. ; ;

FORMULAS FOR LOWERING THE DEGREE OF TRIGONOMETRIC FUNCTIONS

1. 
2. 
3. 
4. 

CONDITIONAL TRIGONOMETRIC IDENTITIES

If A + B + C = 180° (or π), or A, B, C are angles of a triangle. Then

1. sin (A + B) = sin (π – C) = sin C, etc .
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 

GRAPHS OF TRIGONOMETRIC FUNCTIONS

1. Graph of y = sin x

2. Graph of y = cos x

3. Graph of y = tan x

4. Graph of y = cot x

5. Graph of y = sec x and y = cosec x

  

6. Graph of y = 3 cos 2x

In a similar way graph of other similar trigonometric functions can be obtained

Since the period of cos x is 2π. Therefore the period of cos 2x is . Also –3 ≤ 3 cos 2x ≤ 3. The graph of y = 3 cos 2x is drawn for a period, i.e. for 0 ≤ x ≤ π. The complete graph is simply the repetition of this portion.

TABLE FOR THE VALUES OF TRIGONOMETRIC RATIOS OF SOME IMPORTANT ANGLES

TABLE -1

TABLE - 2

EXPRESSIONS OF SINAND COS IN TERMS OF Sin A

We have 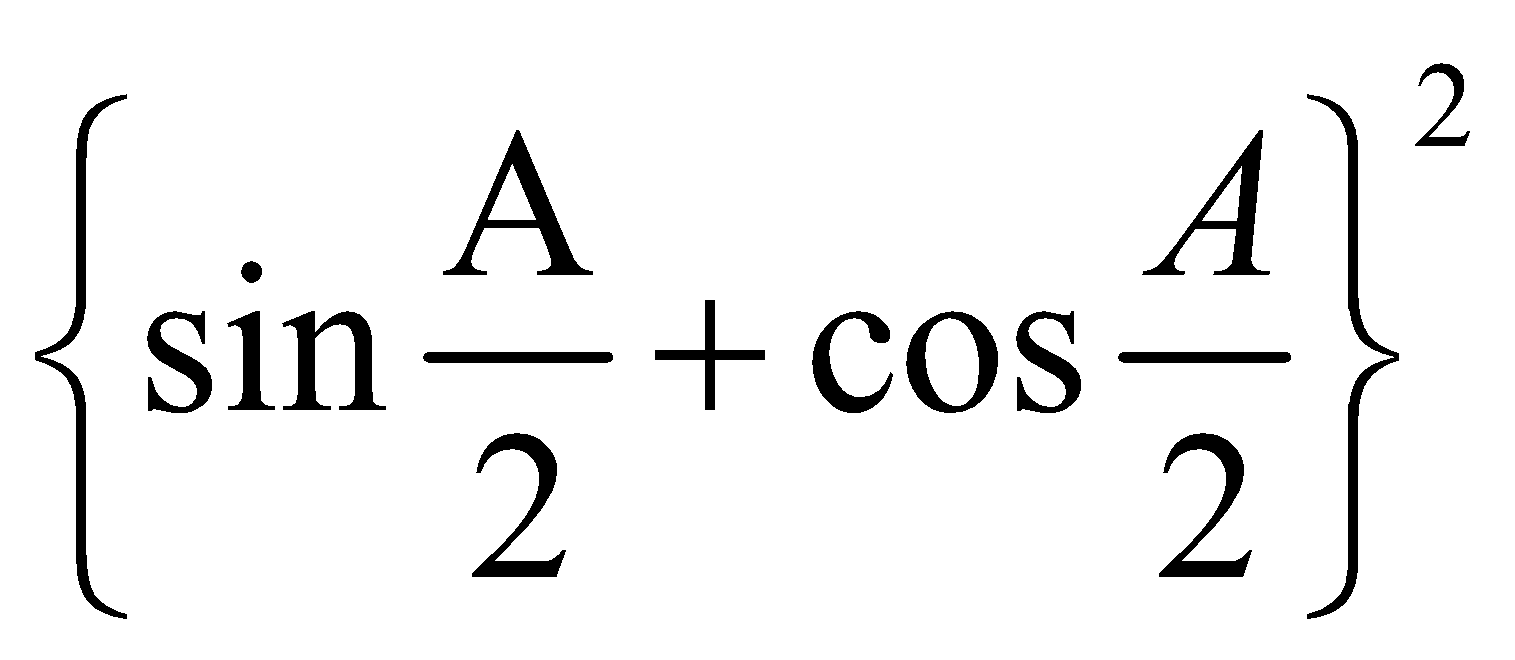= 1 + sinA and  = 1 – sinA

So that   = and =

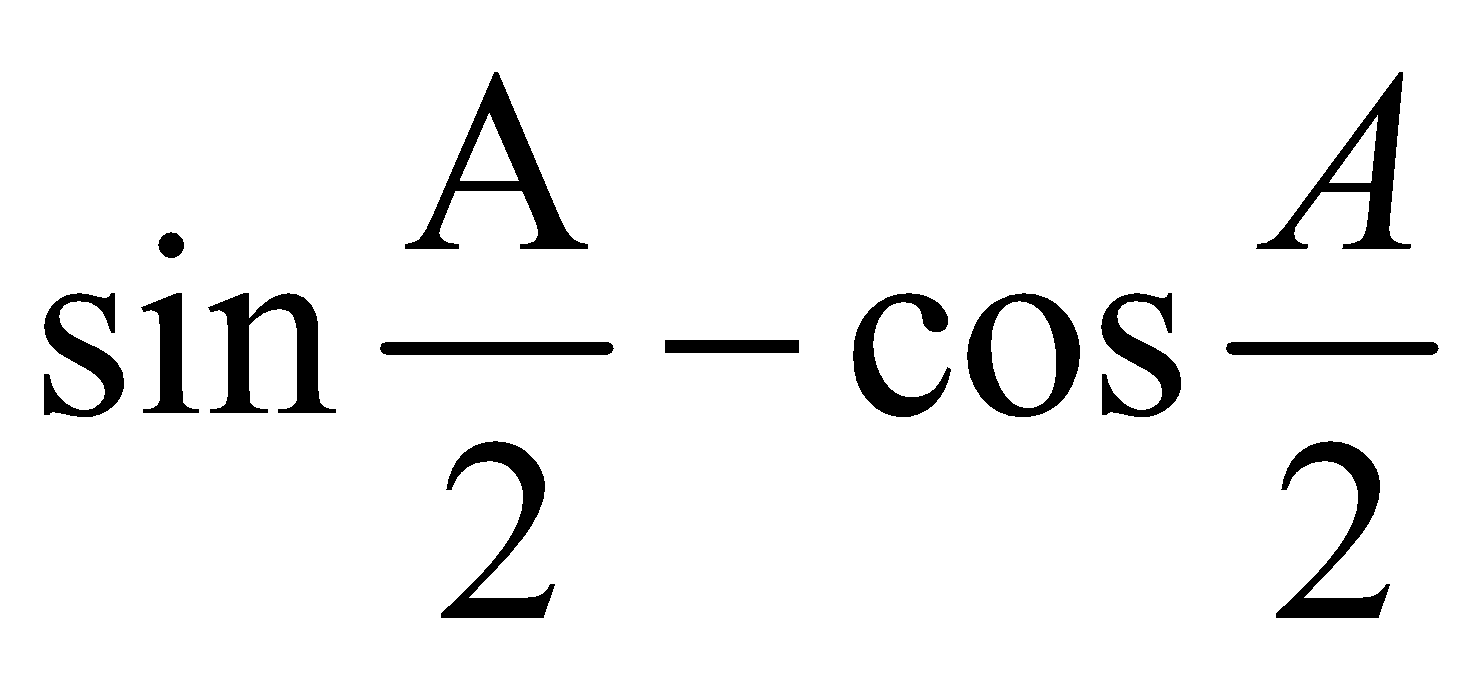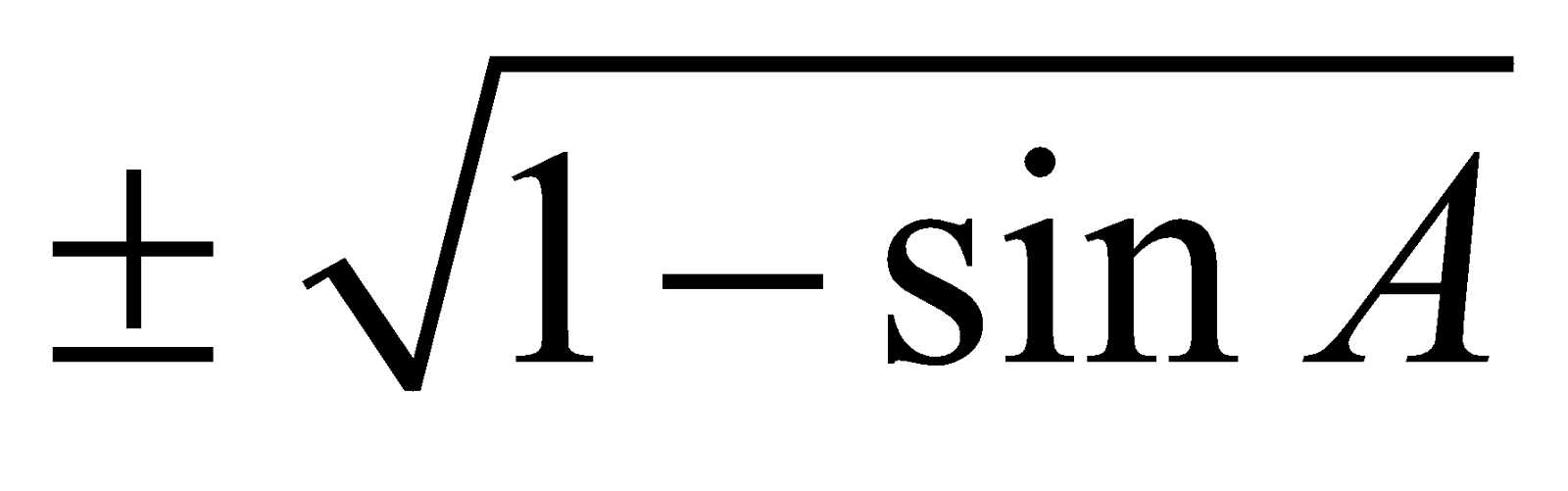
By adding and subtracting, we have

2 sin =   ...(i)

and 2 cos =   ...(ii)

In each of the formulae (i) and (ii) there are two ambiguous signs.

To find these ambiguities we proceed as follows :

We have,   sin + cos =

The RHS of this equation is positive if

i.e. if,

Hence 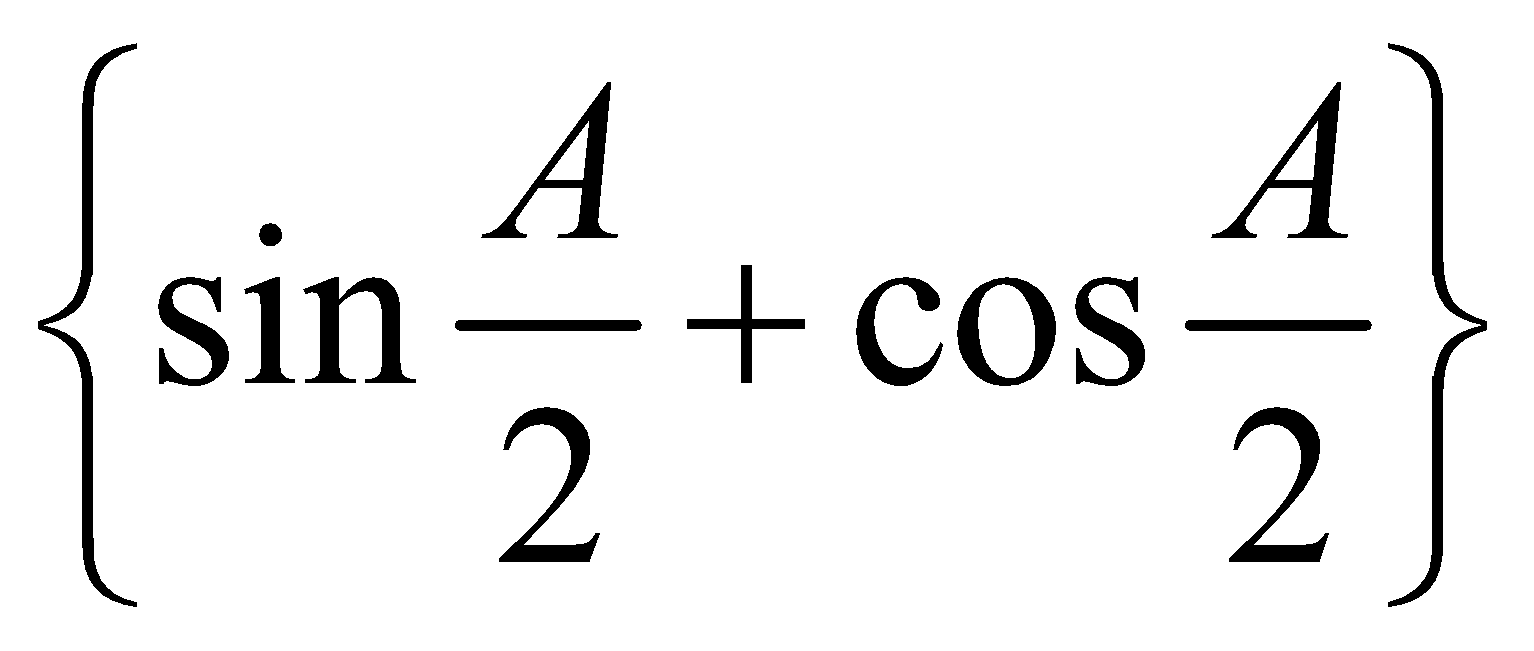is positive if 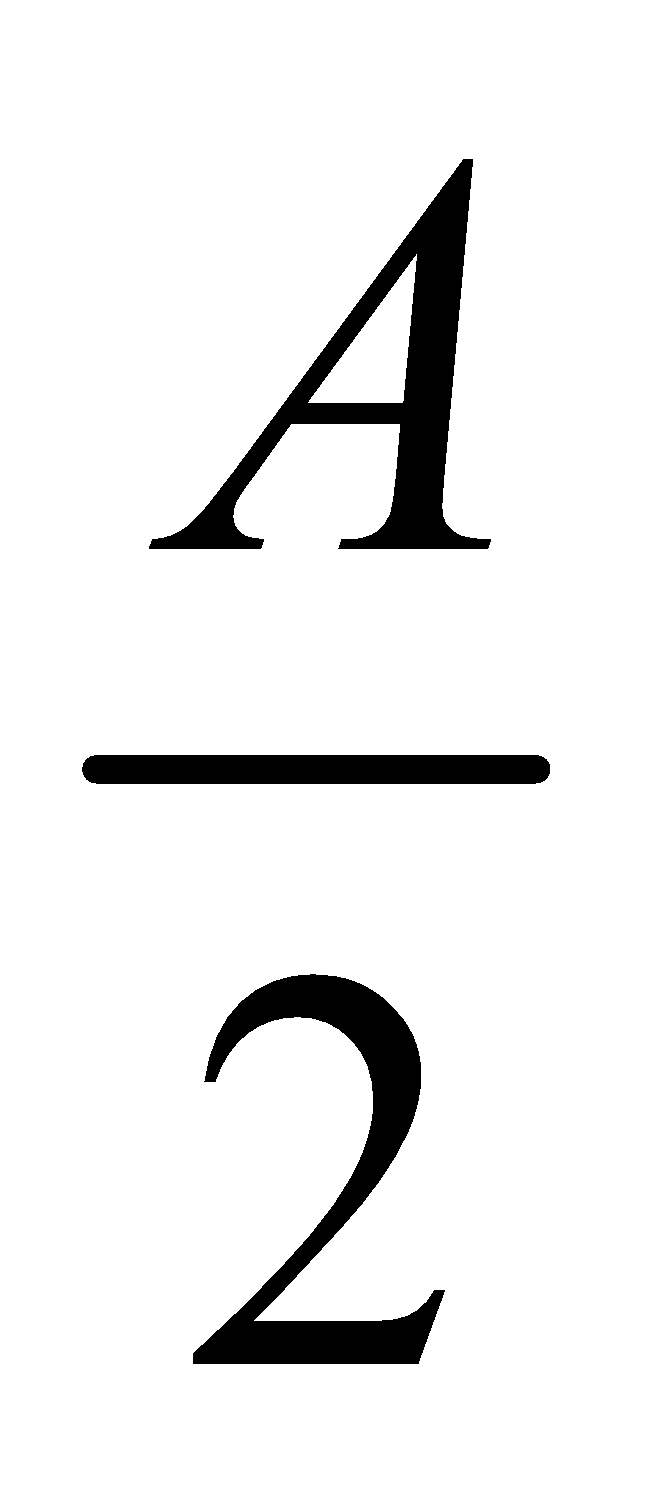 lies between  and  and it is negative otherwise.

Similarly, 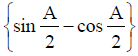is positive if  lies between and  and otherwise it is negative.

These results can be shown graphically as given in the following figure :

PERIODIC FORM OF a sinθ + b cosθ AND MINIMUM AND MAXIMUM VALUES

Let y = a sin θ + b cos θ.   Put a = r cos α and b = r sinα   then

y  = r (sinθ cosα +  cosθ sinα) = r sin (θ + α), where

Alternatively, if we put a = r sin β.  b = r cos β, then

Now, consider

We know that ;  

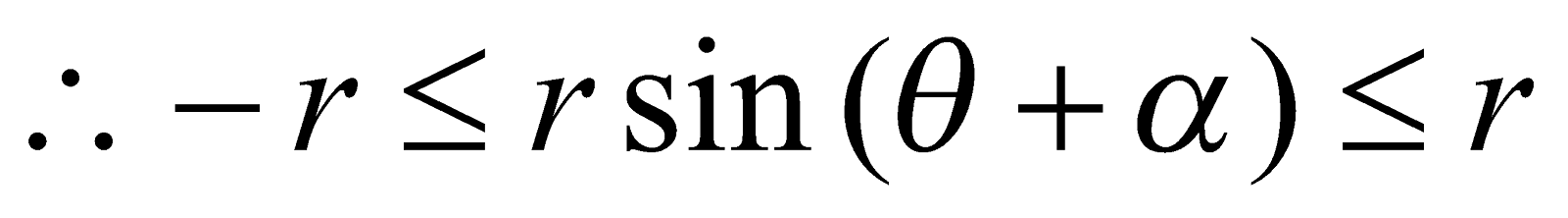
∴ Maximum value of  and   Minimum value of

Also,  

TO FIND THE SUM OF THE SINES OF A SERIES OF ANGLES, THE ANGLES BEING IN ARITHMETIC PROGRESSION

Let the angles be

Let

We have

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

and

By adding together these n lines, we have

The other terms on the right -hand sides canceling one another.

Hence, we have

i.e., S

TO FIND THE SUM OF THE COSINES OF A SERIES OF ANGLES, THE ANGLES BEING IN ARITHMETIC PROGRESSION

Let the angles be  

Let  S ≡ cos α + cos (α + β) + cos (α + 2β) + ...... +
cos {α + (n – 1) β}

We have

,

. . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

and    

By adding together these n lines, we have

The other terms on the right-hand sides cancelling one another. Hence, we have

2S × sin= 2 cos

i.e.          S =

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT