INFINITE SERIES
BINOMIAL THEOREM FOR ANY INDEX
If | x | < 1, then for any n
The following are some important properties of this expansion:
- In this expansions there are infinitely many terms.
- This expansion is valid for | x | < 1 and first term unity.
- The general term of this expansion is
- When x is small compared with 1, we see that the terms finally get smaller and smaller. If x is very small compared with 1, we take 1 as a first approximation to the value of (1 + x)n or 1 + nx as a second approximation.
- Replacing n by –n in the above expansion, we get
Replacing x by –x in this expansion, we get 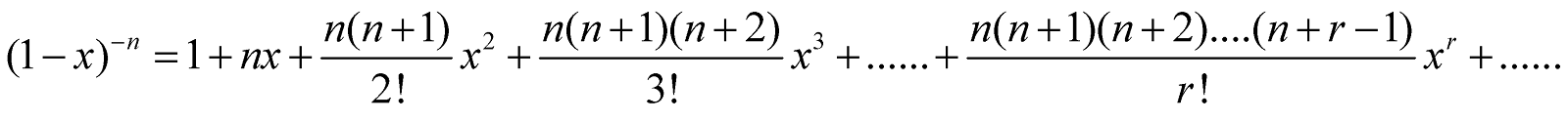
Hence,
EXPONENTIALS
The number e
By the Binomial Theorem, if n > 1,
= 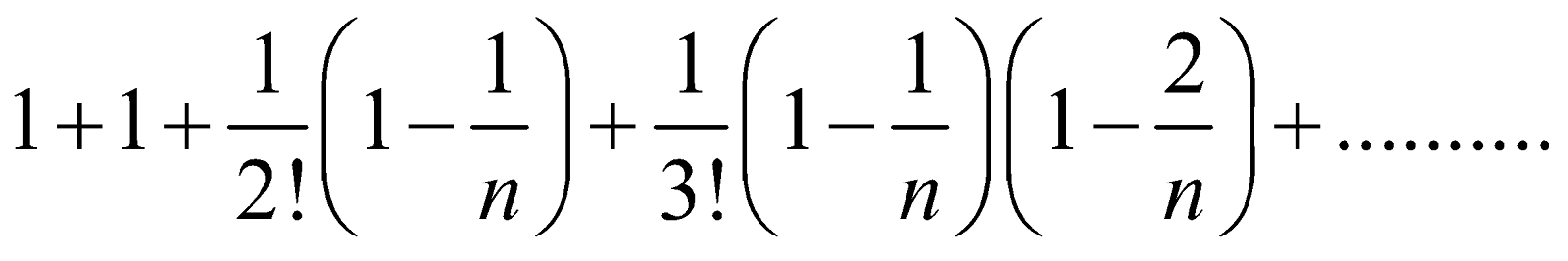
If n is indefinitely large, then etc. Then the right hand side =
etc. Then the right hand side = 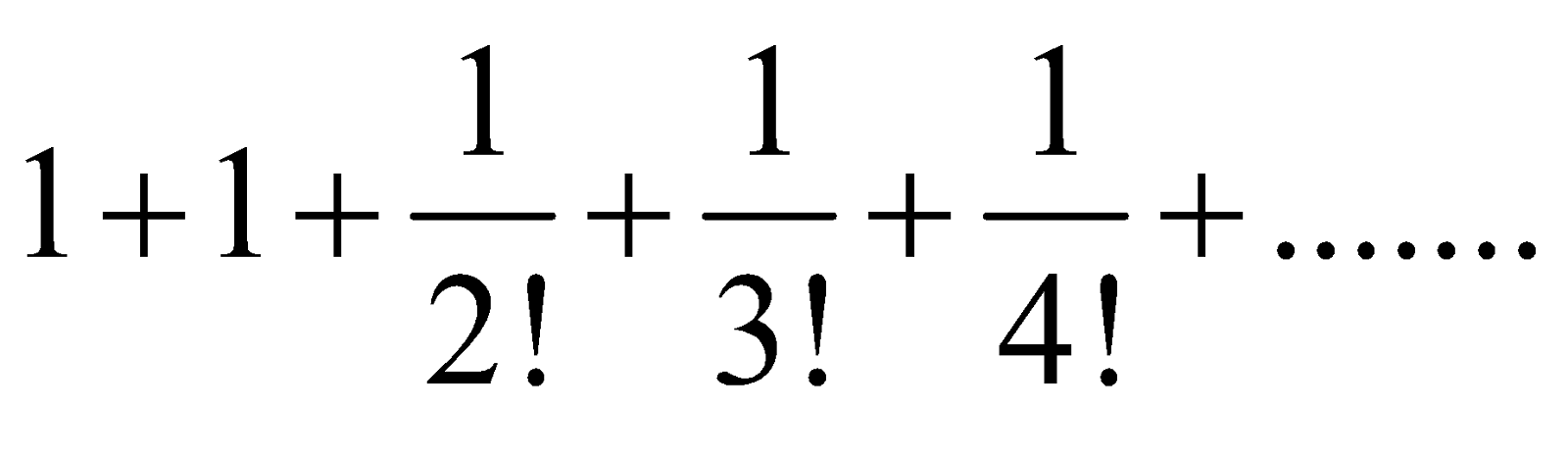
Thus, the limiting value of 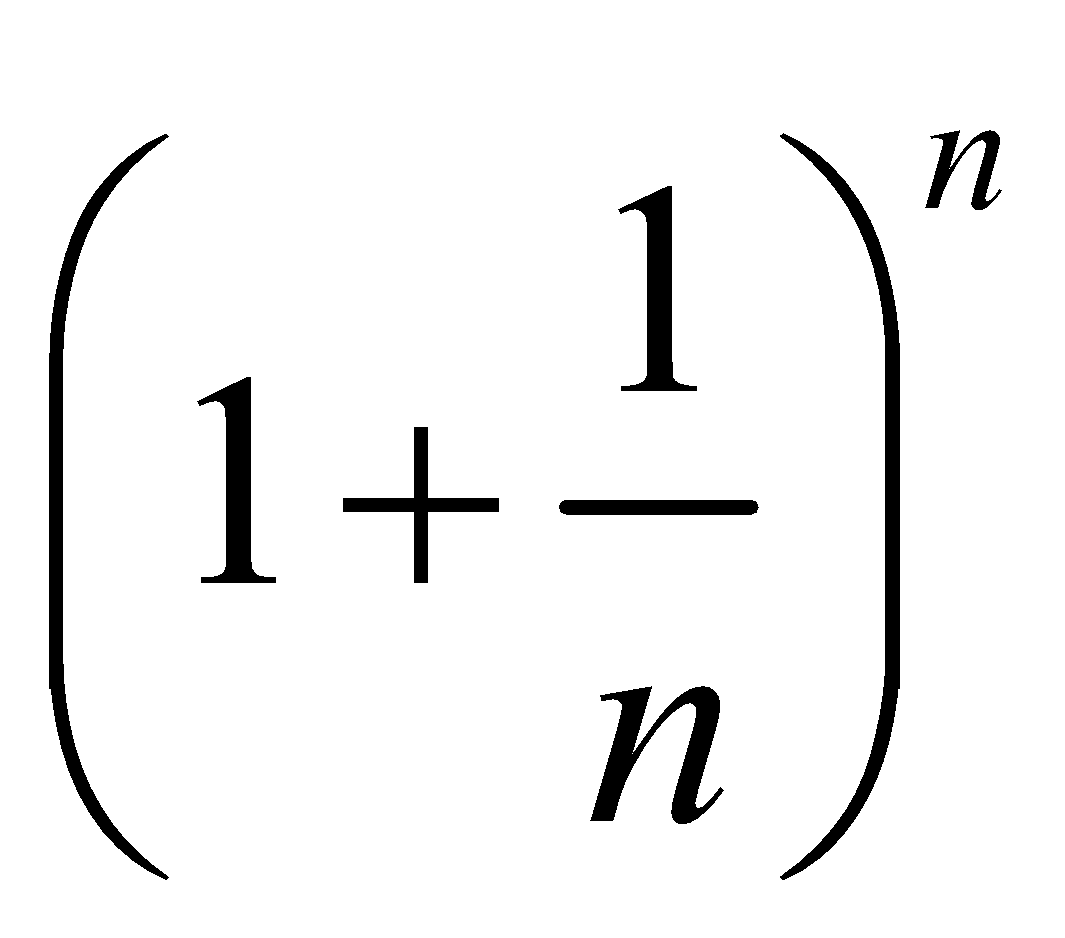 when n is infinite, is the sum of the series
when n is infinite, is the sum of the series 
The sum of this series is denoted by the letter 'e'. Hence, we have,
RESULTS :
- e is an irrational number.
- 2 < e < 3. The approximate value of e is e = 2.71828.
EXPONENTIAL SERIES
To prove that 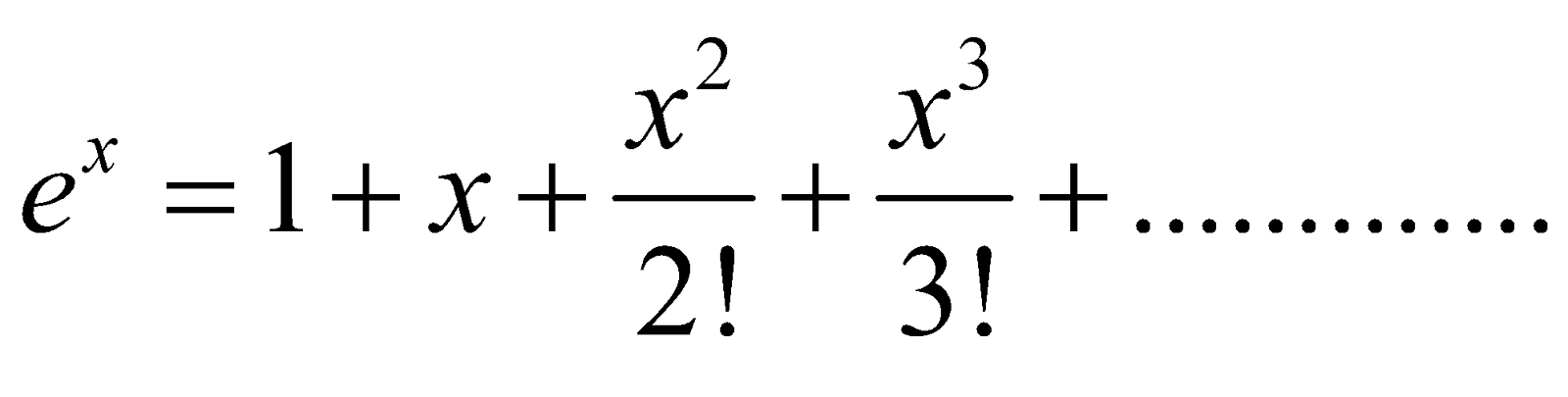
If n is natural number greater than 1, then for any x,
or 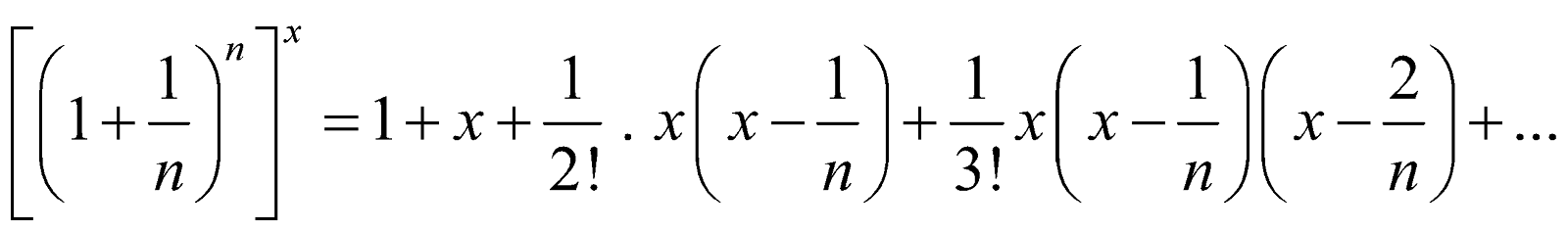
Taking limit as  , we get
, we get
To expand ax in ascending powers of x
We have 
Let ec = a so that c = loge a.
Then ax = ec x = 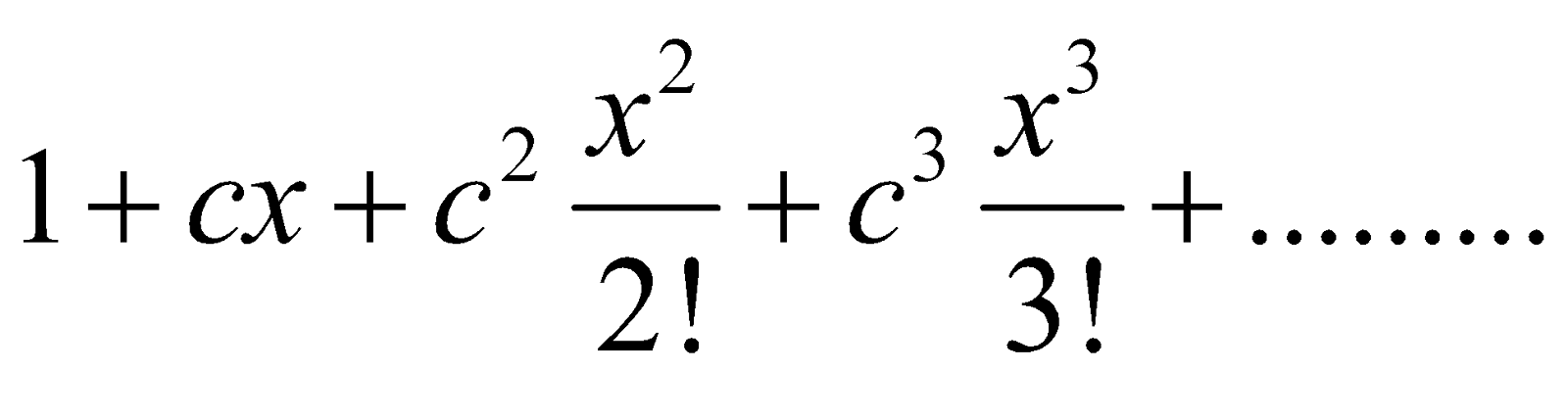
or 
This is called the exponential theorem.
SOME IMPORTANT FORMULAE
Note :
(i)
(i)
(ii) 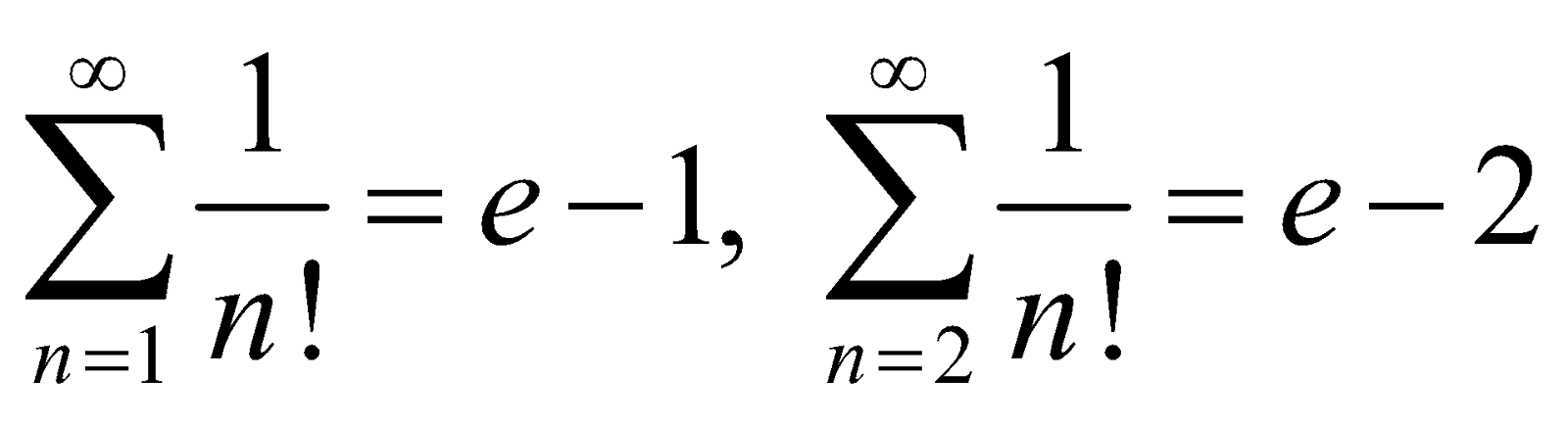
LOGARITHMS (DEFINITION)
For each positive real number , the unique real number m is called the logarithm of b to the base a written as logab, if am = b.
, the unique real number m is called the logarithm of b to the base a written as logab, if am = b.
- Thus logab = m, if and only if am = b, 'log' being the abbreviation of the word 'logarithm'.
- The following properties of logarithm follow immediately from the definition :
loga 1 = 0 because a0 = 1
loga a = 1 because a1 = a
loga ax = x because ax = ax
- Moreover, as a is a positive real number, b is also a positive real number. Thus, we define the logarithm of only a positive real number to a positive real number base other than 1. Negative numbers and zero have no logarithms. The expressions log (–2), log 0,
are meaningless.
LAWS OF LOGARITHMS
If a > 0 and , then
- Change of base : For any positive real numbers r and b,
,
for any positive x and c not equal to 1.
LOGARITHMIC SERIES
If a is positive, then by the exponential theorem, we have
ay = 1 + y loge a + 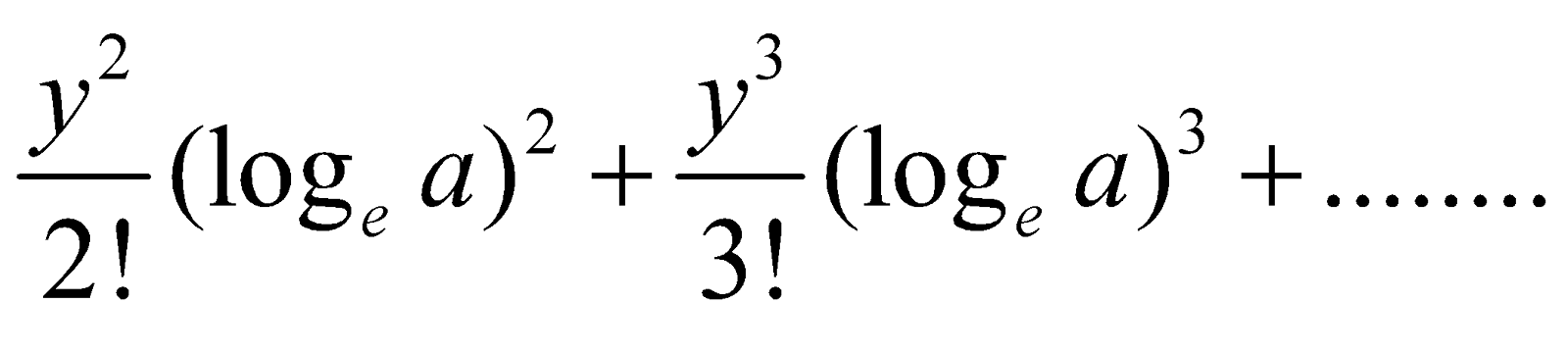
Putting a = 1 + x, we get
If | x | < 1, then by Binomial theorem, we have
= 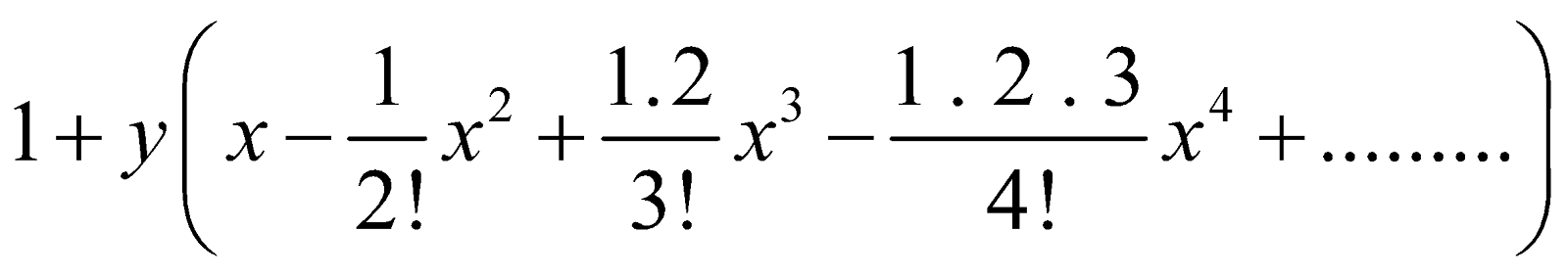 + terms involving higher powers of y
+ terms involving higher powers of y
Thus,
This is an identity in y, therefore, equating coefficients of y on both sides we get
This is known as the Logarithmic Series.
SOME IMPORTANT RESULTS
On Subtracting (2) from (1), we get
(–1 < x < 1)
CALCULATION OF LOGARITHMS
We have
Suppose we have to find loge2. Putting 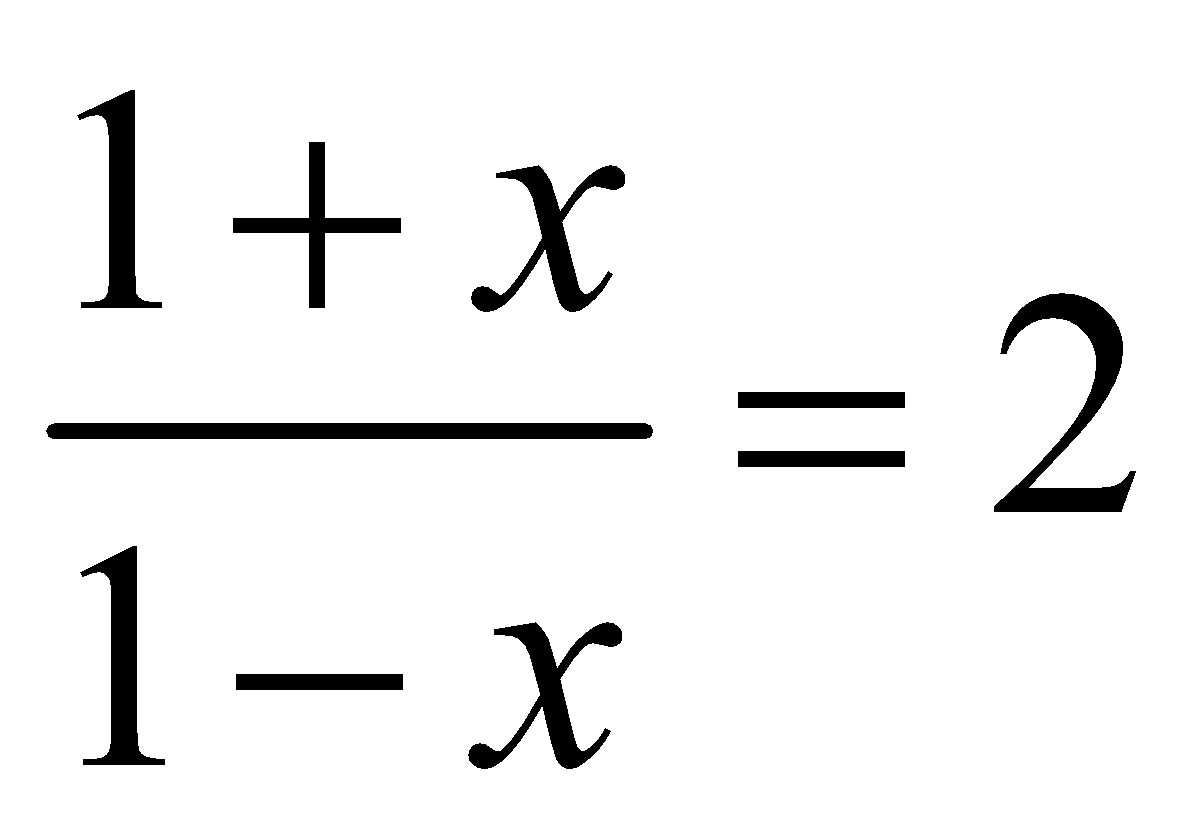 , we get
, we get 
On putting  in (1), we get
in (1), we get
Similarly, we can find 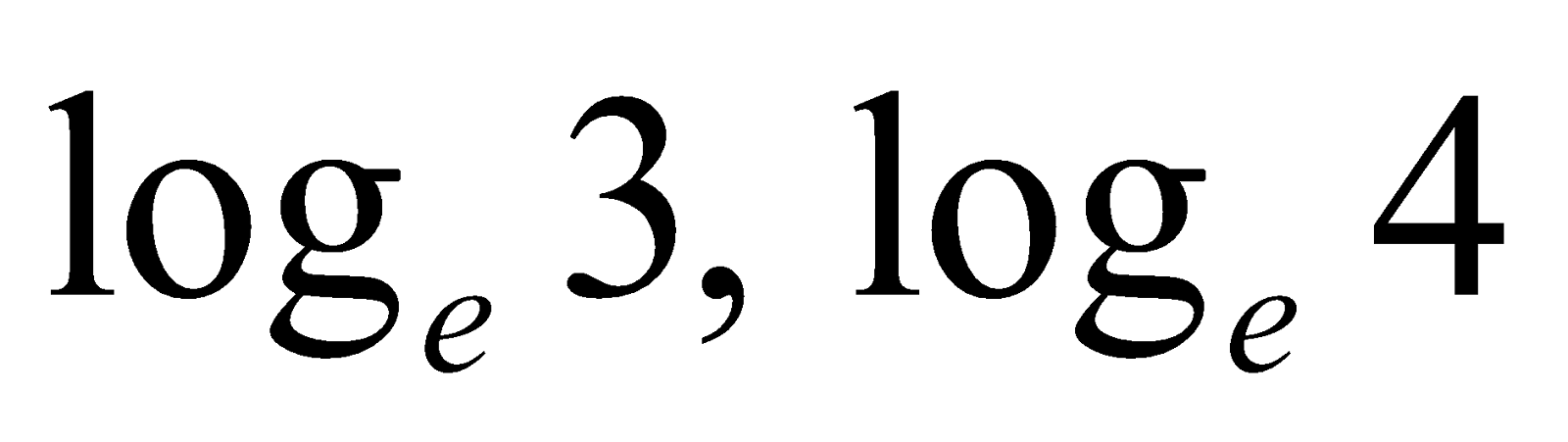 and so on.
and so on.
Logarithms of numbers calculated to the base e are called NAPERIAN LOGARITHMS or NATURAL LOGARITHMS.
Logarithms to the base 10 are called COMMON LOGARITHMS.
Hence, the logarithms of any number to the base 10 can be obtained by multiplying the logarithms of the number to the base e by 0.43429448.
Also we have 2 < e < 3
And logex is an increasing function, therefore log 2 < loge e < log 3 log 2 < 1 < log 3.
Example :
Prove that 
Solution :
We have, 







