PROPERTIES OF TRIANGLES, HEIGHTS AND DISTANCES
REPRESENTATIONS IN A TRIANGLE
In any triangle ABC, the side BC, opposite to the angle A is denoted by a, the side CA and AB opposite to the angles B and C respectively are denoted by b and c respectively.
Semi perimeter of the triangles is denoted by s and its area by Δ or S. In this unit, we shall discuss various relations between the sides a, b, c, and the angles A, B, C, of ΔABC.
Further, in geometry we are familiar with the following relations
- A + B + C = π
- a + b > c
- b + c > a
- c + a > b
SINE RULE
In any Δ ABC, the sines of the angles are proportional to the lengths of the opposite sides,
i.e. 
Note 1 : The above rule can also be written as
Note 2 : The rule is generally used to express sides of the triangle in terms of sines of angles and vice-versa as discussed below.
Let 
Then a = k sin A, b = k sin B, c = k sin C or
COSINE FORMULAE
In any Δ ABC,
PROJECTION FORMULAE
In any Δ ABC,
a = b cos C + c cos B
b = c cos A + a cos C
c = a cos B + b cos A
TRIGONOMETRIC RATIOS OF HALF OF THE ANGLES OF A TRIANGLE
In any Δ ABC, we have
AREA OF A TRIANGLE
Similarly,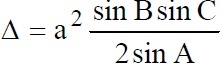 and
and 
NAPIER’S ANALOGY
In any triangle ABC
EXPRESSING SINES OF ANGLES IN TERMS OF SIDES AND AREA
EXPRESSING TANGENTS AND COTANGENTS OF ANGLES IN TERMS OF SIDES AND AREA
,
,
,
COTANGENT RULES
On the base BC of the triangle ABC, take a point D, such that
BD : DC = m : n, ∠BAD = α , ∠CAD = β and ∠ADB = θ, then
BD : DC = m : n, ∠BAD = α , ∠CAD = β and ∠ADB = θ, then
(m + n) cot θ = n cot β – m cot α
(m + n) cot θ = m cot C – n cot B
These results are frequently used in statics.
CIRCLES CONNECTED TO A TRIANGLE
CIRCUMCIRCLE OF A TRIANGLE
The circle, which passes through the angular points of a triangle ABC, is called its circumcircle. The centre of this circle is the point of intersection of perpendicular bisectors of the sides and is called the circumcentre. Its radius is always denoted by R. The circumcentre may lie within, outside or upon one of the sides of the triangle.
Circumradius : The radius of the circumcircle of a triangle ABC is called the circumradius given by
INSCRIBED CIRCLE OR INCIRCLE OF A TRIANGLE
The circle, which can be inscribed within the triangle so as to touch each of its sides, is called its inscribed circle or incircle. The centre of this circle is the point of intersection of bisectors of the angles of the triangle. The radius of the circle is always denoted by r and is equal to the length of the perpendicular from its centre to any of the sides of triangle.
Inradius : The radius of the inscribed circles of a triangle is called the in-radius. It is denoted by r and is given by
ESCRIBED CIRCLES OF A TRIANGLE
The circle, which touches the side BC from outside and two sides AB and AC produced of a triangle ABC is called the escribed circle opposite to the angle A. Its radius is denoted by r1. Similarly r2 and r3 denote the radii of the escribed circles opposite to the angles B and C respectively.
The centres of the escribed circles are called the ex–centres. The centre of the escribed circle opposite to the angle A is the point of intersection of the external bisectors of angles B and C. The internal bisector of A also passes through the same point. This centre is generally denoted by I1.
FORMULAE FOR r1, r2, r3
In any  , we have
, we have
- r1 =
, r2=
, r3 =
- r1 =
; r2=
; r3 =
- r1 =
; r2=
; r3 =
- r1 = 4 R sin
cos
cos
; r2= 4 R cos
sin
cos
; r3 = 4 R cos
cos
sin
ORTHOCENTRE OF A TRIANGLE
Let the perpendiculars AL, BM and CN from the vertices A, B and C on the opposite sides BC, CA and AB of ΔABC, respectively, meet at O′. Then O′ is the orthocentre of the ΔABC
The triangle LMN is called the pedal triangle of the ΔABC.
IMPORTANT RESULTS
- The distances of the orthocentre of the triangle from the vertices are 2RcosA, 2RcosB, 2RcosC and its distances from the sides are 2RcosB cosC, 2RcosC cosA, 2RcosA cosB.
- Circumradius of the pedal triangle
- Area of the pedal triangle
- Lengths of the medians AD, BE and CF of ΔABC are given by
- Circumcentre O, centroid G and orthocentre O' are collinear and G divides OO′ in the ratio 1 : 2.
- Distance between the circumcentre O and the incentre I is
Where I1, I2, I3 are the centres of the escribed circles opposite to the angles A, B and C respectively.
CYCLIC QUADRILATERAL
A quadrilateral is a cyclic quadrilateral if its vertices lie on a circle.
- Area of cyclic quadrilateral ABCD is
where 
- Circumradius of cyclic quadrilateral
and similarly other angles.
- Ptolemy’s Theorem : If ABCD is a cyclic quadrilateral, then AC.BD = AB.CD + BC.AD
i.e in a cyclic quadrilateral the sum of the products of the lengths of opposite sides is equal to the product of its diagonals.
REGULAR POLYGON
A polygon is called a regular polygon if all its sides are equal and its angles are equal.
Note :
- If a polygon has ‘n’ sides, sum of its internal angles is
and each angle is
.
- In a regular polygon the centroid, the circumcentre and the incentre are same.
- Area of a regular polygon
where a is length of side, n is number of sides of polygon, R is radius of circumscribing circle and r is the radius of incircle of the polygon.
SOLUTION OF TRIANGLES
In a triangle there are six elements, viz., three sides and three angles. In plane geometry we have done that if three of the elements are given at least one of which must be a side, then the other three elements can be uniquely determined. The procedure of determining unknown elements from the known elements is called solving a triangle.
SOLUTION OF A RIGHT ANGLED TRIANGLE
Case I. When two sides are given:
Let the triangle be right angled at C. Then we can determine the remaining elements as given in the following table:
Given Required
(i) a, b tan A =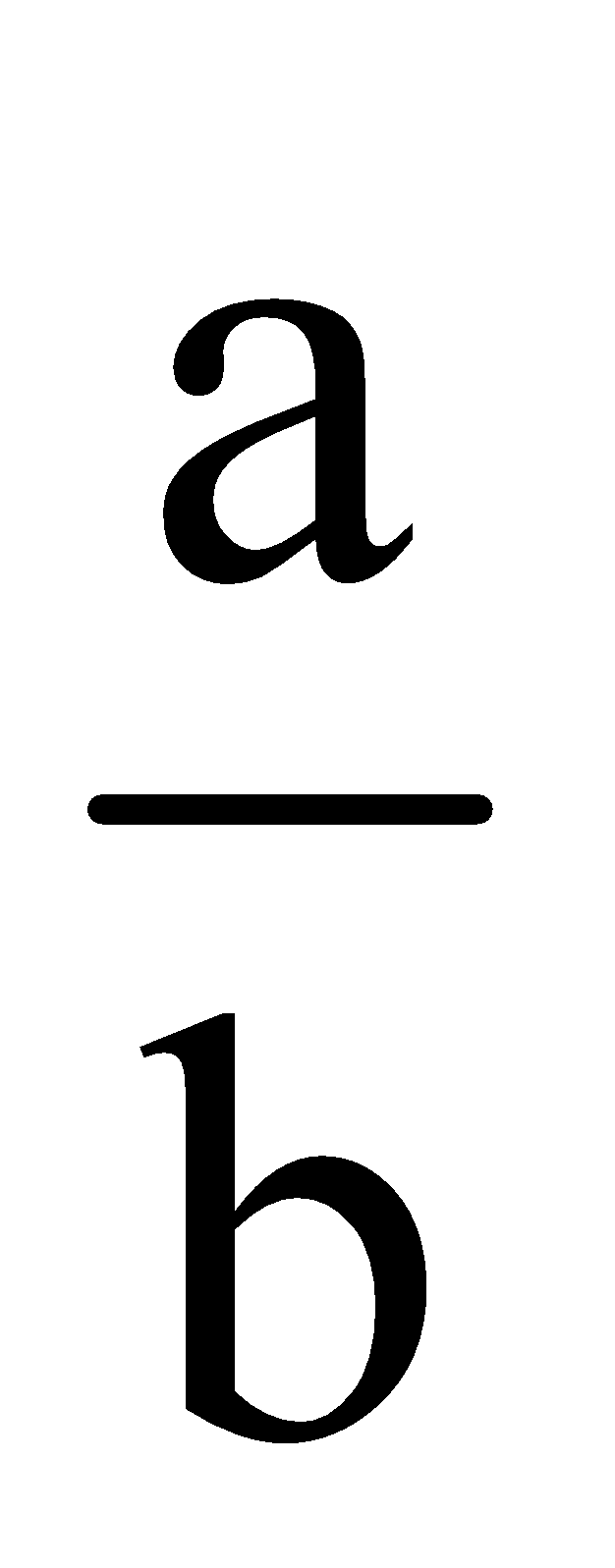 , B = 900–A, c =
, B = 900–A, c = 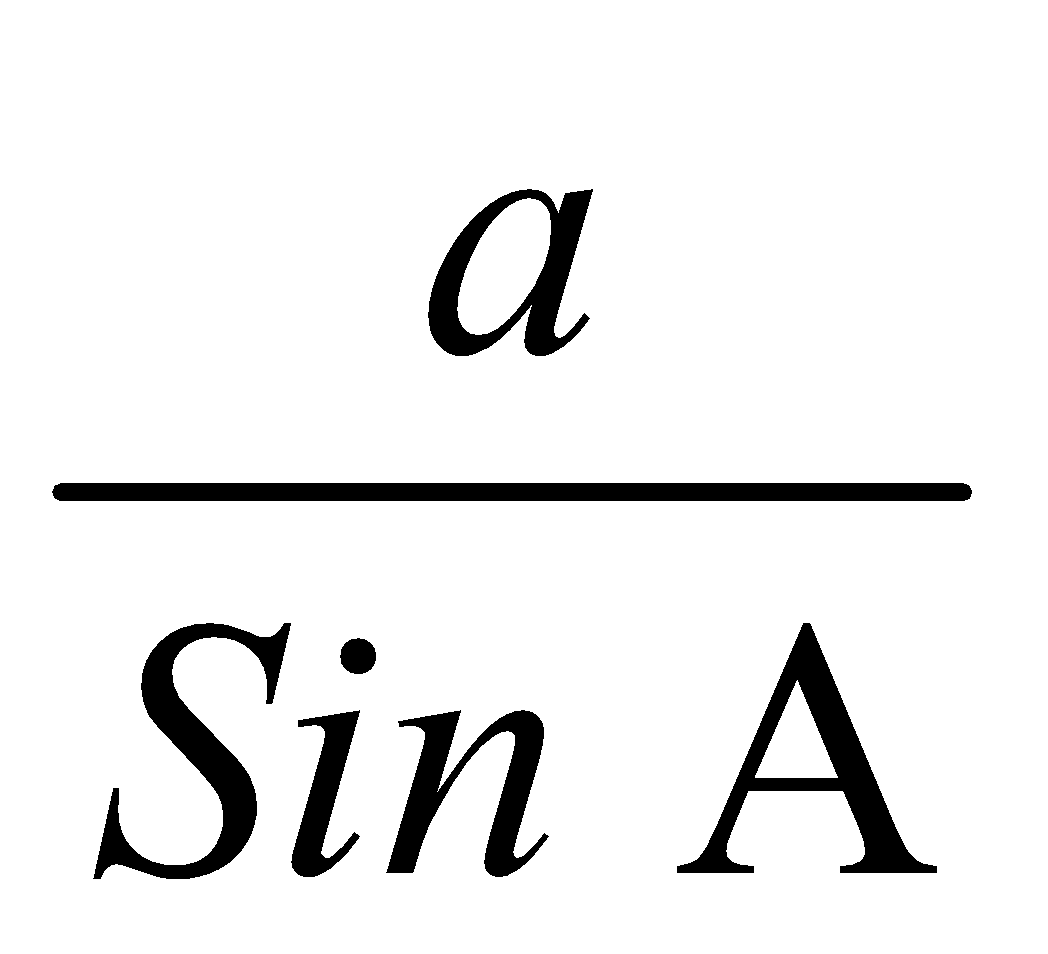
(ii) a, c Sin A = 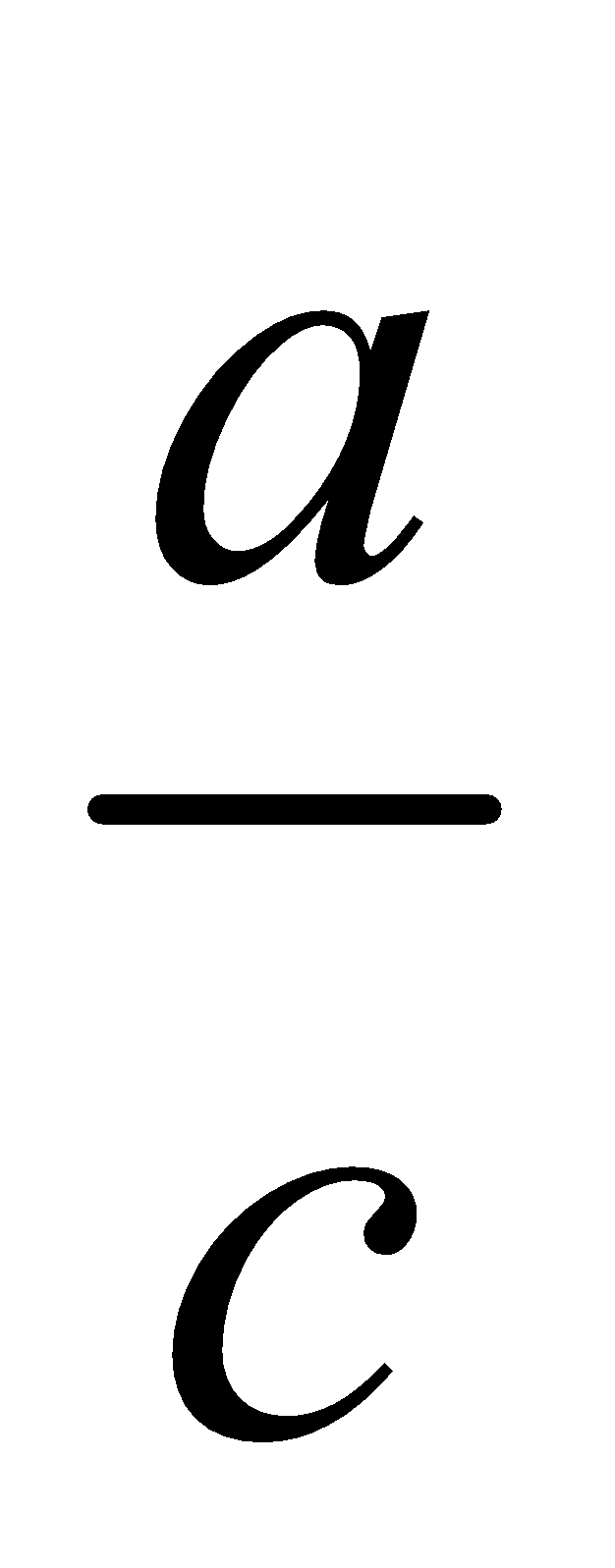 , B = 900–A, b = c cos A
, B = 900–A, b = c cos A
Case II. When a side and an acute angle are given:
In this case we can determine the remaining elements as given in the following table:
Given Required
(i) a, A B = 900–A, b = a cot A, c = 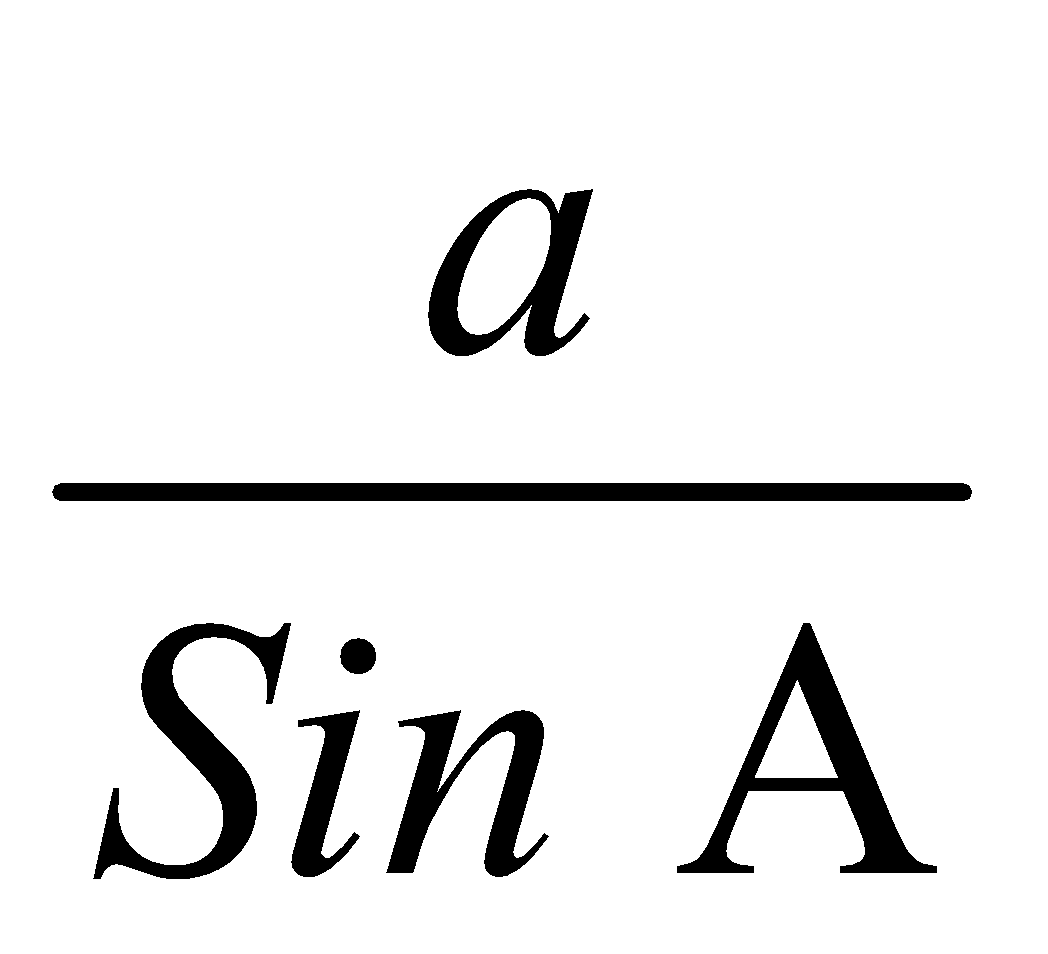
(ii) c, A B = 900–A, a = c sin A, b = c cos A
SOLUTION OF TRIANGLES IN GENERAL
Case I. When three sides a, b and c are given:
In this case the remaining elements are determined by using the following formulae:
sin A = 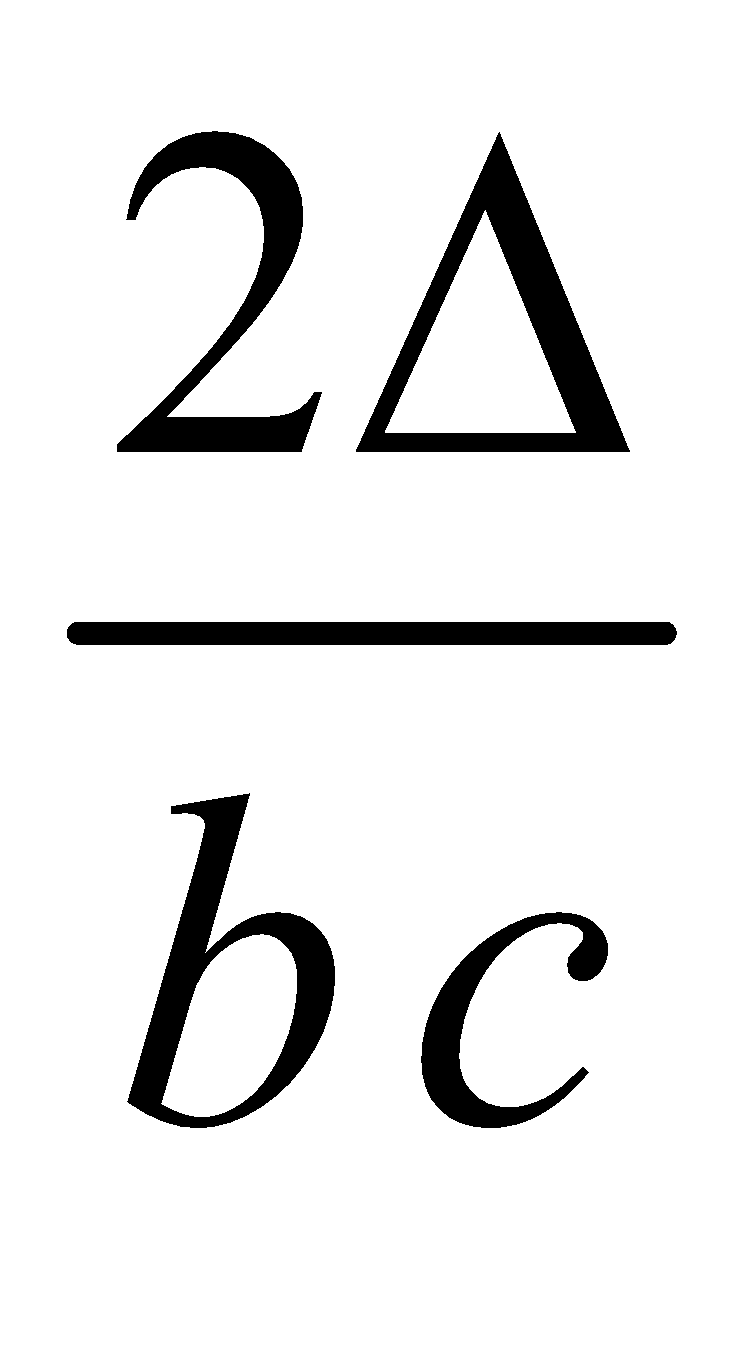 , sin B =
, sin B = 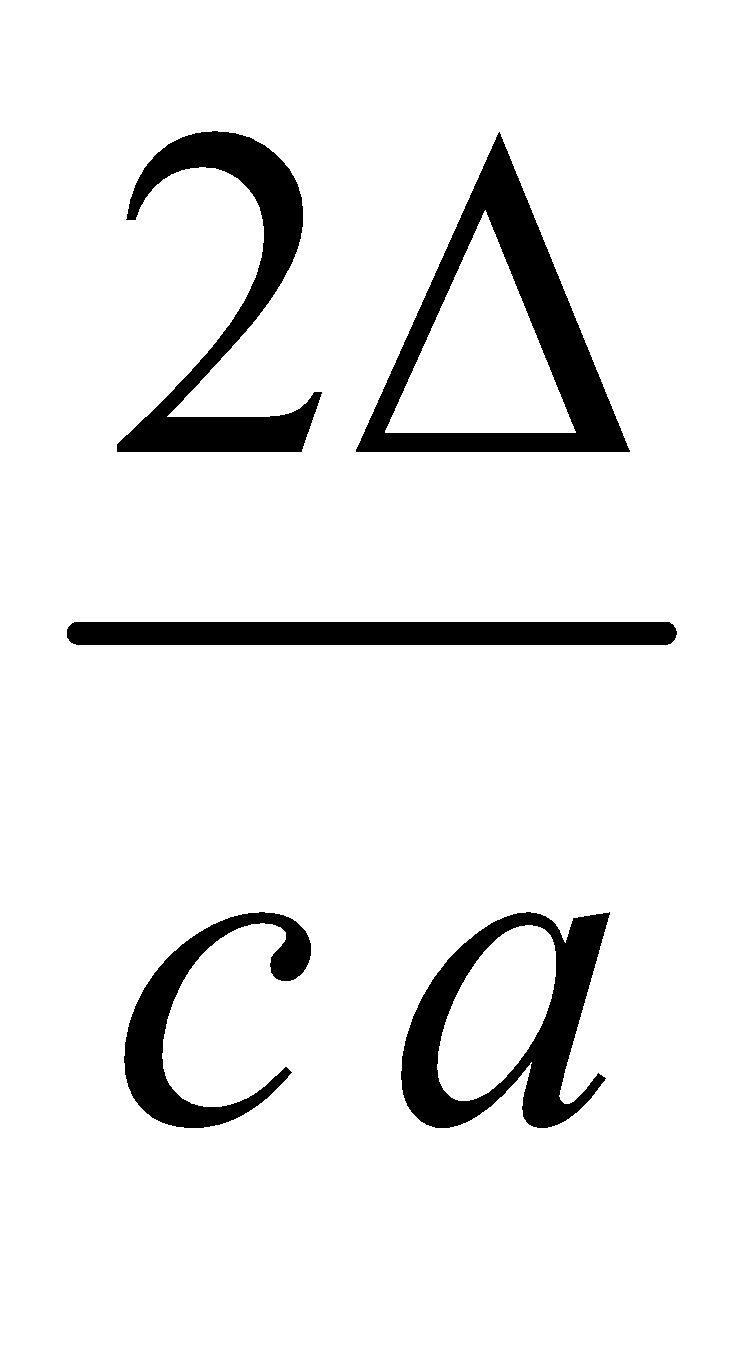 , sin C =
, sin C = 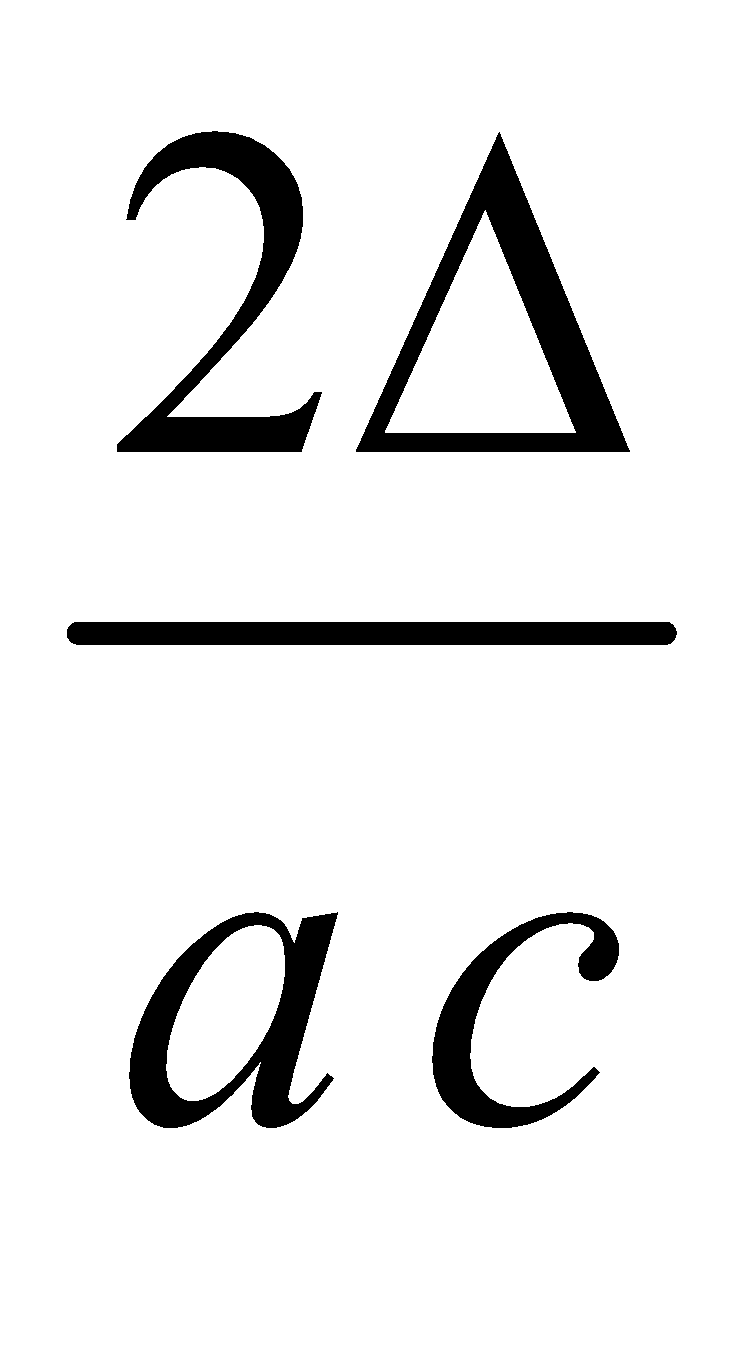
or tan  =
= , tan
, tan 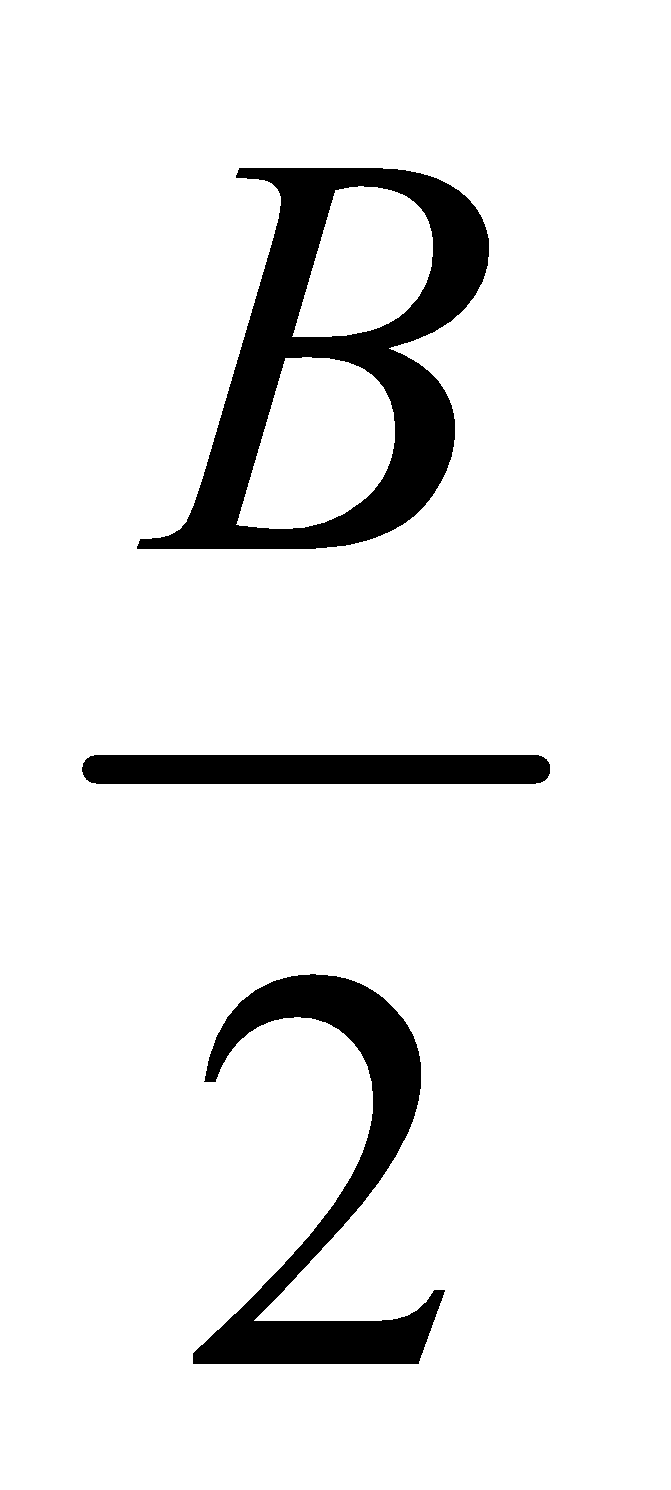 =
= 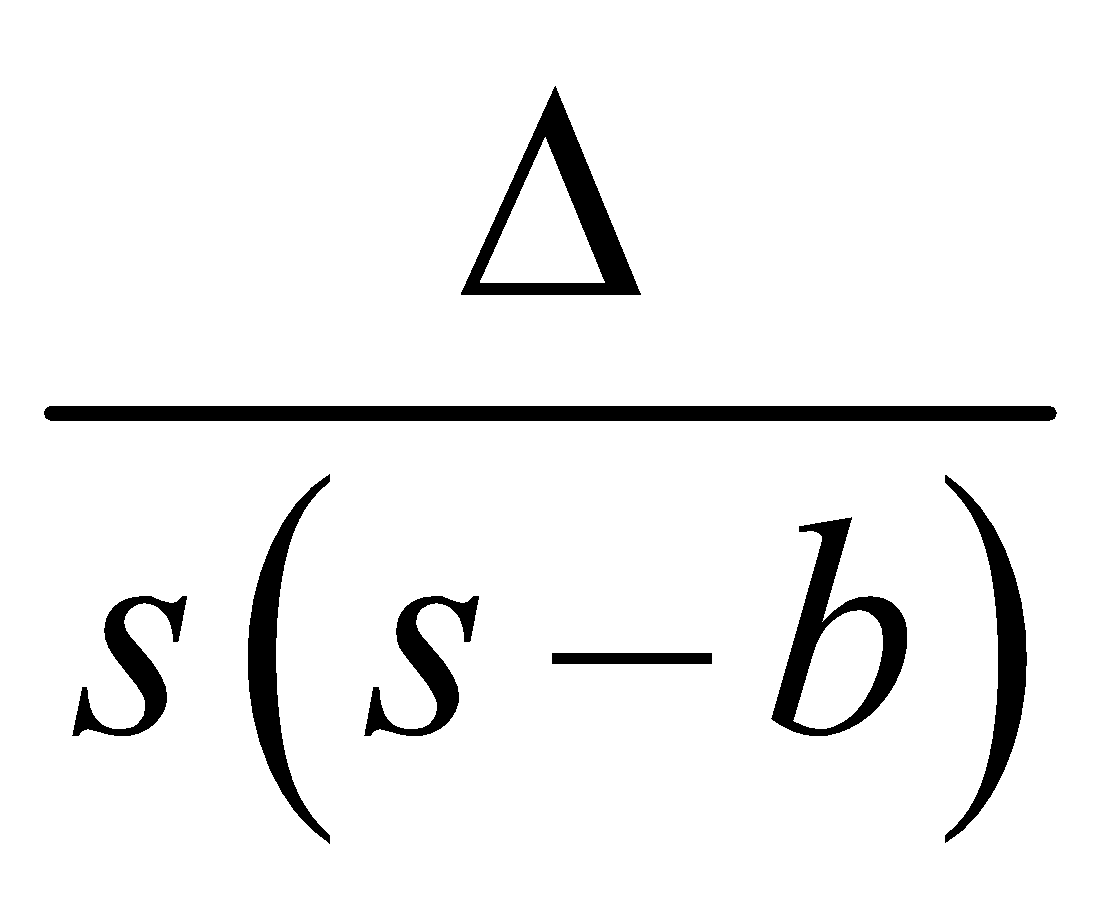 , tan
, tan 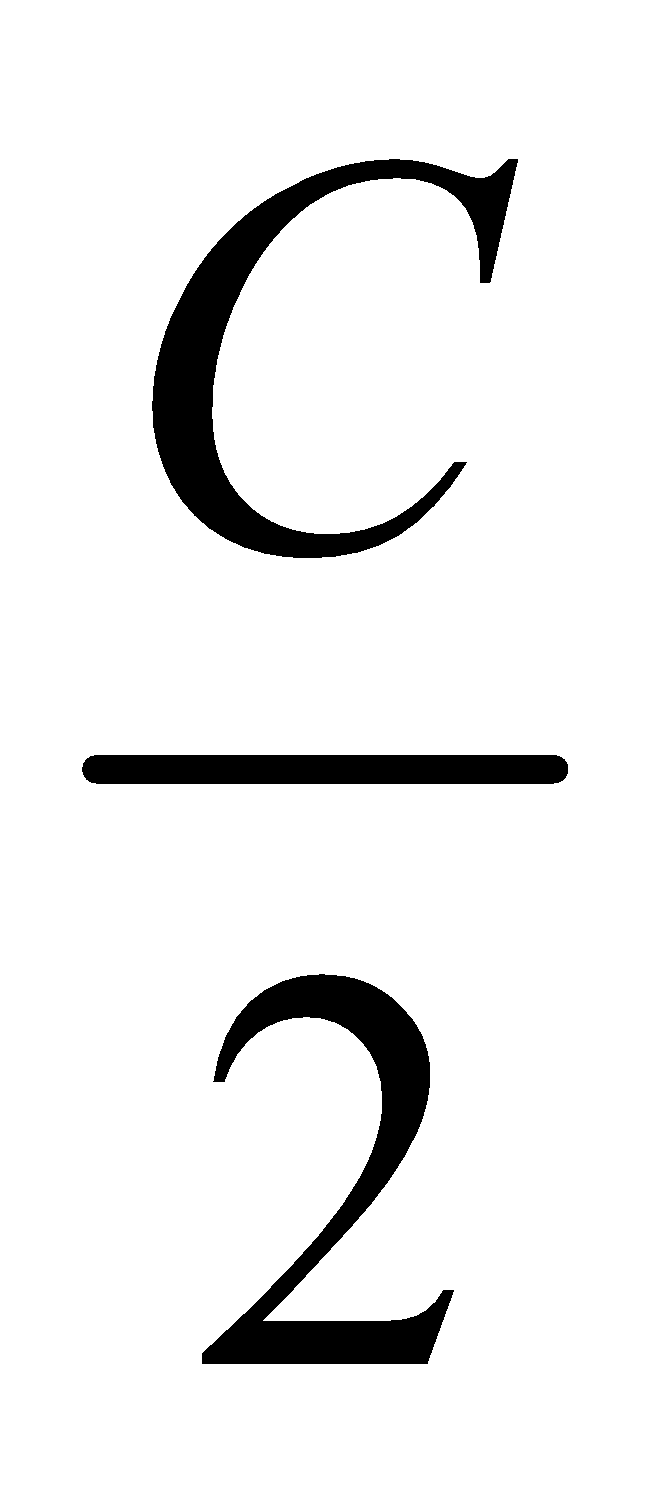 =
= 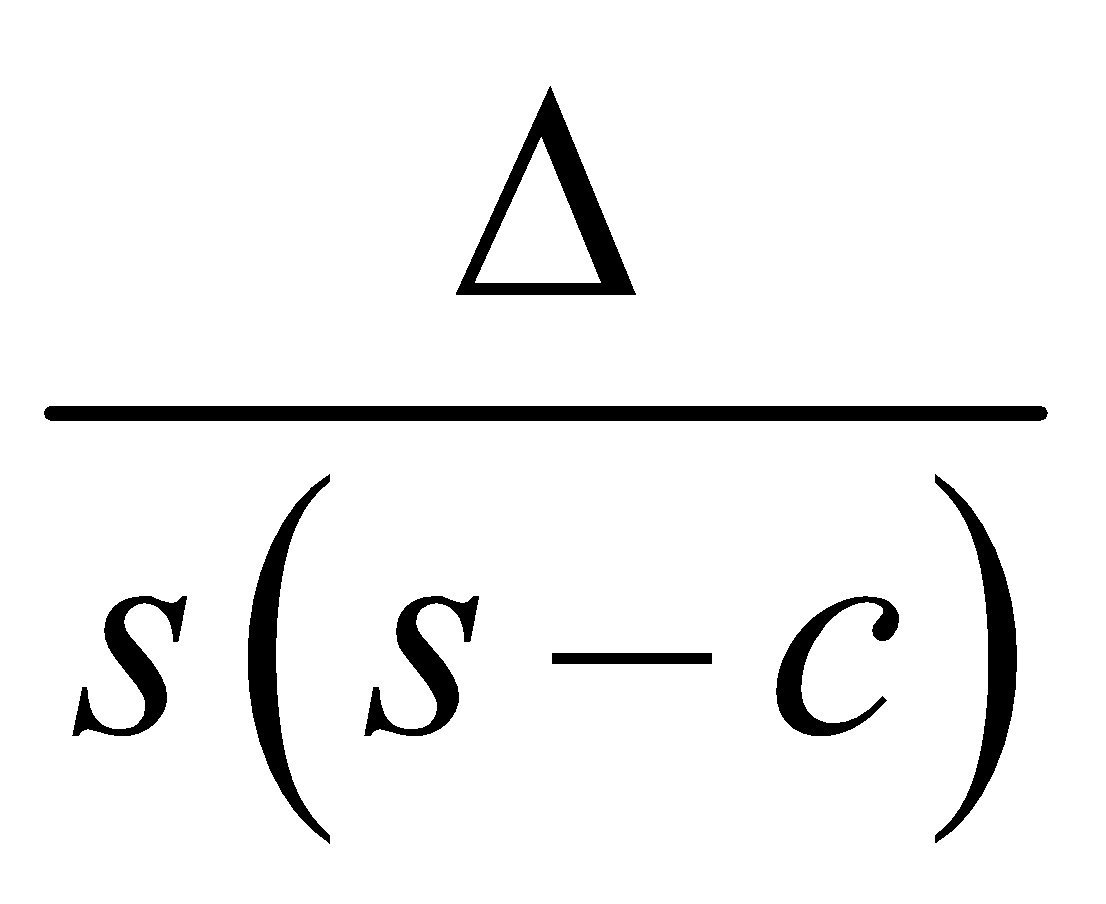
And A + B + C = 1800
Cosine formulae can also be used to find the angles.
Case II. When two sides a, b and the included angle C are given :
In this case we use the following formulae:
tan  =
=  cot
cot 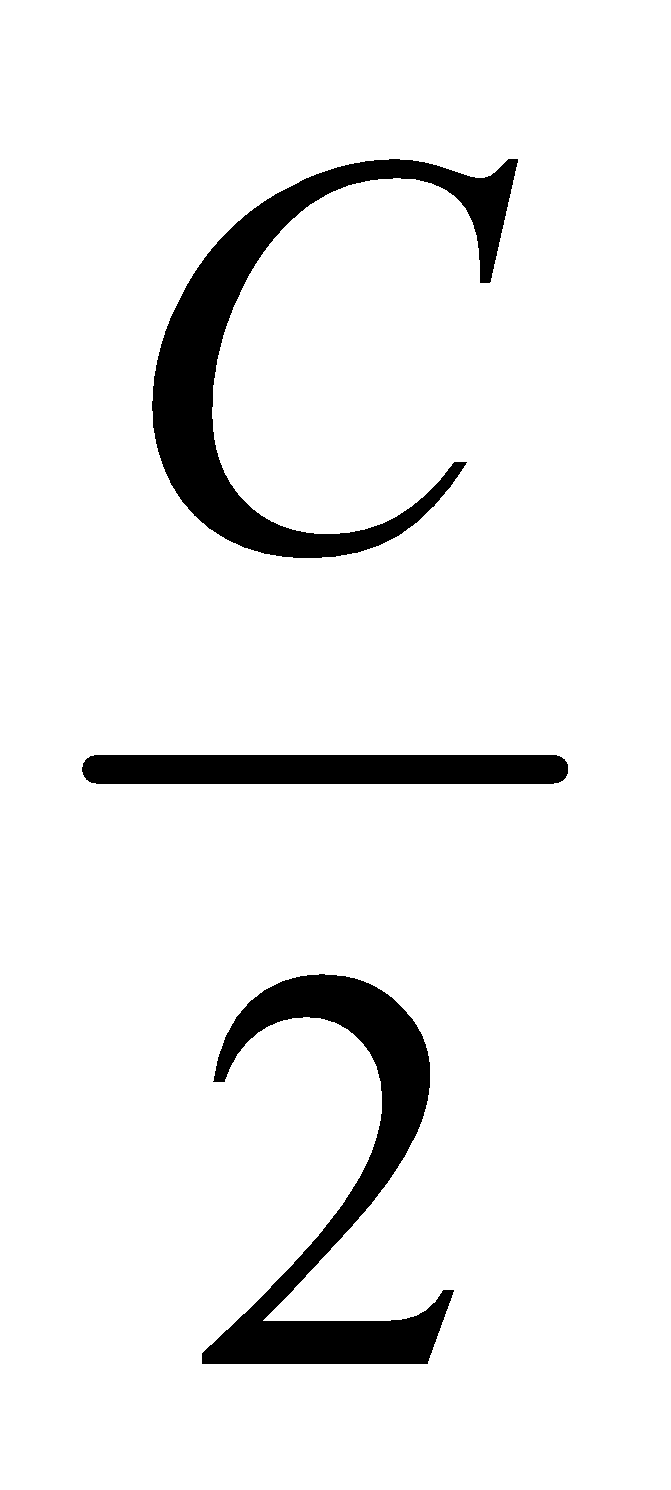 , if b > a
, if b > a
Case III. When one side a and two angles A and B are given:
In this case we use the following formulae to determine the remaining elements:
A + B + C = 1800 C = 1800–A – B
b =  and c =
and c =  ,
,  =
=  a b sin C.
a b sin C.
Case IV. When two sides a, b and the angle A opposite to one side is given:
In this case we use the following formulae:
sin B =  ...(I)
...(I)
C = 1800– A – B, c =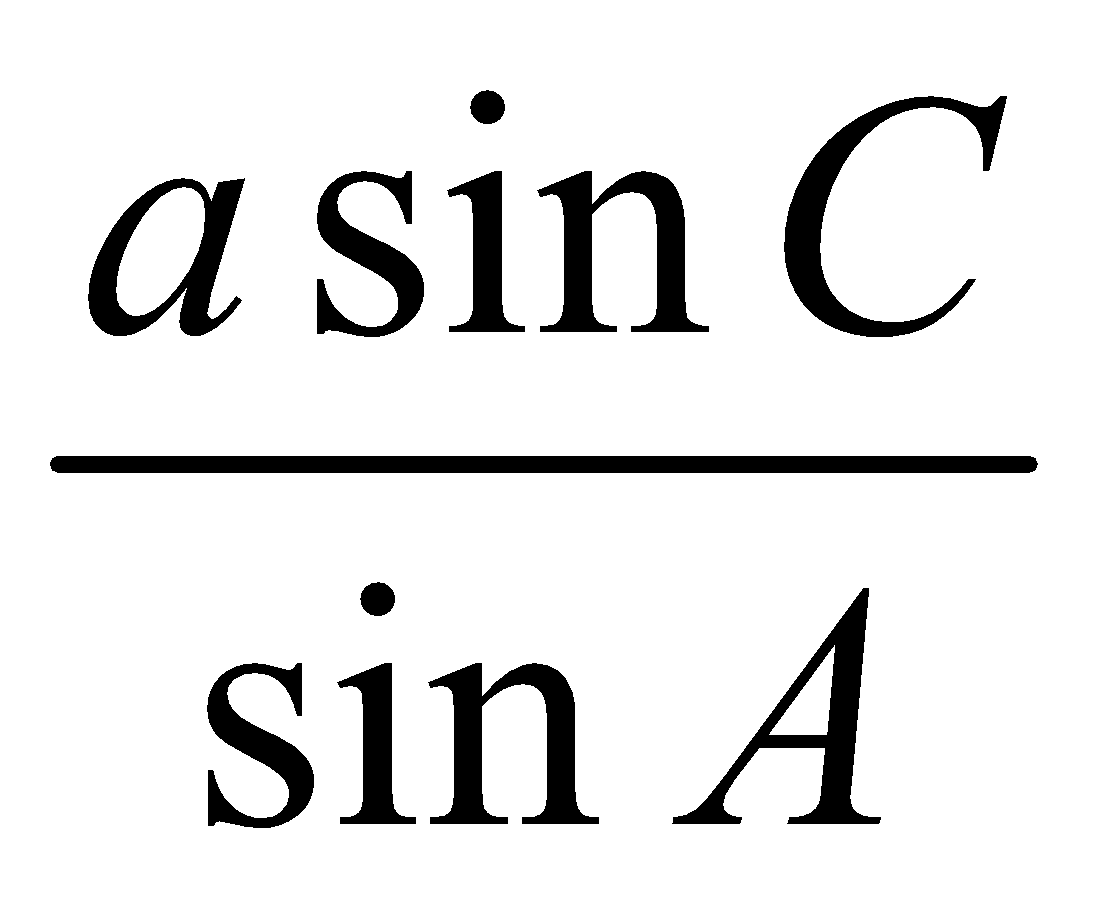
From (I), the following possibilities will arise:
- When A is an acute angle and a < b sin A
In this case the relation 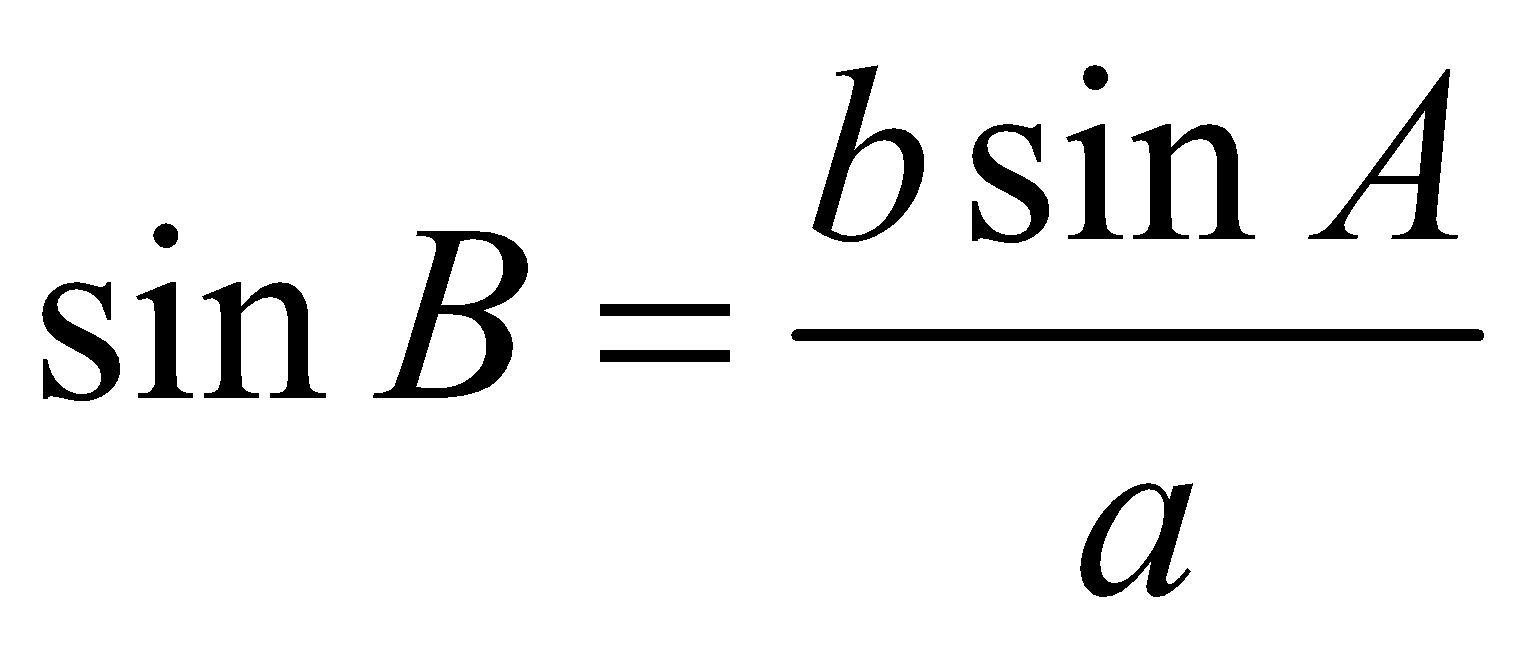 gives that sin B > 1, which is impossible. Hence no triangle is possible.
gives that sin B > 1, which is impossible. Hence no triangle is possible.
- When A is an acute angle and a = b sin A. In this case only one triangle is possible which is right angled at B.
- When A is an acute and a > b sin A. In this case there are two values of B given by , say, B1 and B2 such that
.
Side c can be obtained by using 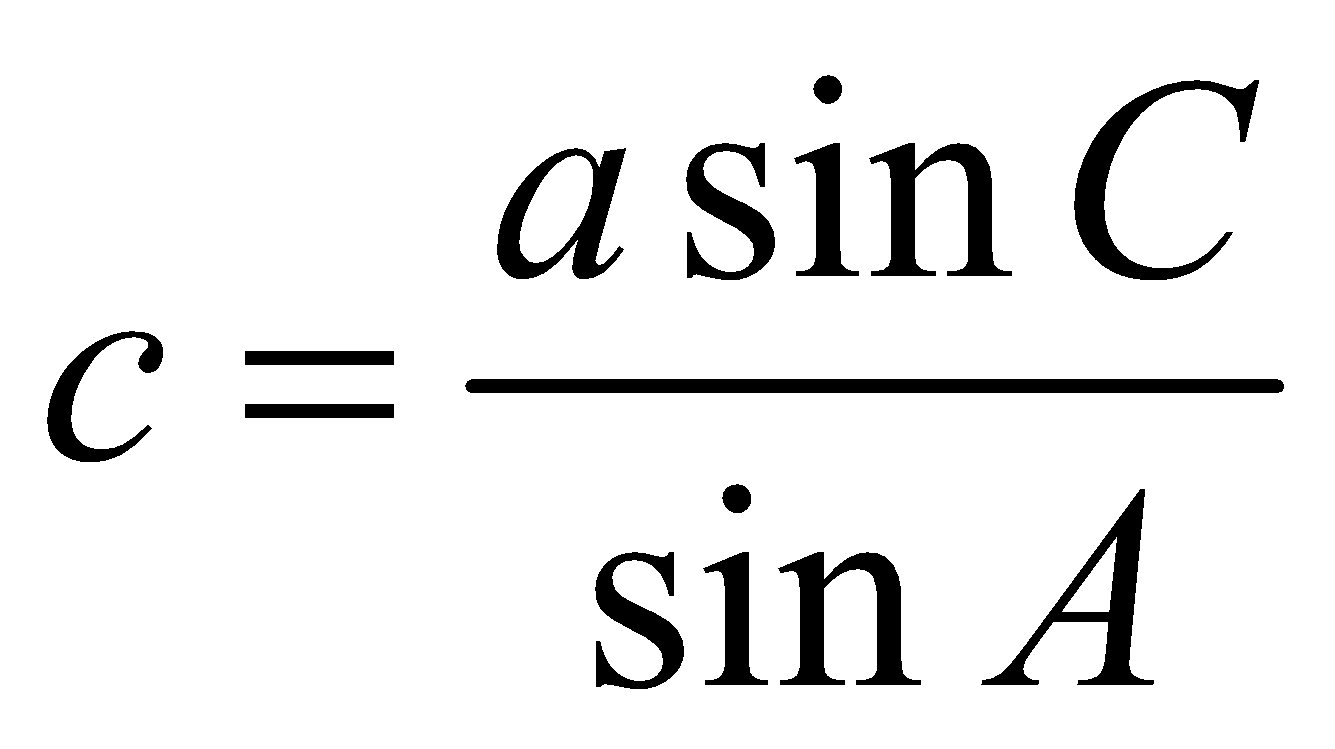 . Hence two triangles are possible. It is called ambiguous case
. Hence two triangles are possible. It is called ambiguous case
SOME IMPORTANT RESULTS
- In any right-angled triangle, the orthocentre coincides with the vertex containing the right-angled.
- The mid-point of the hypotenuse of a right-angled triangle is equidistant from the three vertices of the triangle.
- The midpoint of the hypotenuse of a right angled triangle is the circumcentre of the triangle.
HEIGHT AND DISTANCES
Let an observer at the point O is observing an object at the point P. The line OP is called the LINE OF SIGHT of the point P. Let OA be the horizontal line passing through the position of observer in the same vertical plane with OP. The acute angle AOP, between the line of sight and the horizontal line is known as the ANGLE OF ELEVATION of P, if the object P is above the horizontal plane and the ANGLE OF DEPRESSION of P, if P lies below the horizontal plane, as seen from O.
Obviously, the angle of elevation of P as seen from a point O is equal to the angle of depression of O as seen from P.
TO FIND THE HEIGHT AND THE DISTANCE OF AN INACCESSIBLE TOWER STANDING ON A HORIZONTAL PLANE
Let AB be the tower and B its foot. On the horizontal line through B, take two points P and Q so that the line PQ passes through B. Measure the length PQ.
Let PQ = a.
Let the angles of elevation of the top A of the tower as seen from P and Q be respectively α and β ( β > α) then
Let AB = x, BQ = y.
From Δ APB,
From Δ AQB,
∴ y = x cot β
In the above case, P, Q are on the same side of the tower. If the two points are on the opposite sides of the tower then from the adjoining figure, we get
β need not be greater than α in this case.
Note Here, all the lines AP, AQ, AB are in one plane.
TO FIND THE DISTANCE BETWEEN TWO INACCESSIBLE OBJECTS OR POINTS
Let the distance between two points P and Q be required. Let A and B be two convenient points. Now measure the length AB and calculate the angles PAB, QAB, PBA and QBA.
Let 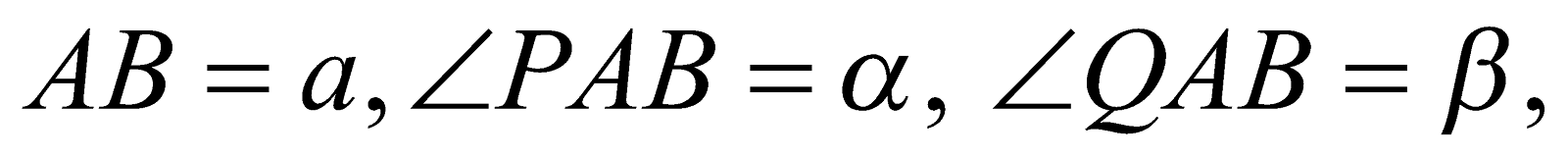
If the lines AP, AQ, AB are coplanar then
If however the lines are not coplanar then measure the ∠PAQ which may not be equal to α – β In any case, we may consider the ∠PAQ as known.
Now, from ΔPAB,
From ΔAQB,
Thus, the sides AP, AQ and the included angle PAQ of the Δ PAQ are determined. Hence AQ can be obtained by the formula : 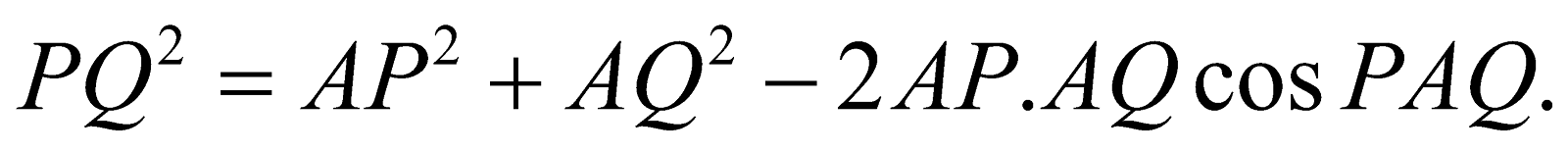
BEARING OF A LINE
The bearing of a horizontal line (i.e., a line in a horizontal plane) is the positive acute angle made by this line with the north-south line in the same horizontal plane.
The amount of eastward or westward deviation of a line from the north-south line measures the bearing of this line. Thus the bearing of the north-south line is zero and that of the east-west line is 90°. In giving the bearing of a line the letter. N or S is written before the angle to show if the line is measured from the northern part or from the southern part of the north-south line and the letter E or W follows the value of the angle to indicate if the line lies to the east or to the west of the north-south line.
Note :
- In the above figure the bearings of the lines OA, OB, OC and OD are respectively N 40°E, S 35°E, S 75° W and N 15°W. Sometimes N 40ºE means the bearing of the point A from the point O. Likewise, for the other points B, C, D, etc.
- Sometimes the acute angle between two lines is called the bearing of one line with respect to the other.
HEIGHTS AND DISTANCES IN THREE DIMENSIONS
PERPENDICULARITY OF A LINE AND A PLANE
- If a line l is perpendicular to a plane π then the line l is perpendicular to any line m in the plane π [see fig. (i)].
[Fig. (i)] [fig. (ii)]
- If a line l is perpendicular to two intersecting lines m and n then the line l is perpendicular to the plane π passing through the lines m and n [see Fig. (ii)]
- PQ is perpendicular to the horizontal plane and the lines QA, QB, QC, .......are in the plane. Then PQ丄QA, PQ丄QB, PQ丄QC,..... Hence the triangles PQA, PQB, PQC..... are all right angled triangles where ∠PQA = 90°, ∠PQB = 90°, ∠PQC = 90°,…….
If the angles of elevation of P at A, B, C, .... are α, β, γ ... then QA = h cot α, QB = h cot β, QC = hcotγ,....
TO FIND THE HEIGHT AND THE DISTANCE OF AN INACCESSIBLE TOWER STANDING ON A HORIZONTAL PLANE.
i.e., measurement in more than one plane
Let AB be a tower and P be any point on the horizontal plane passing through the foot of the tower.
Measure the distance PQ in any suitable direction and also measure the angles ∠APB, ∠APQ, ∠AQP.
Let PQ = a, ∠APB = α, ∠APQ = β, ∠AQP = γ
From 
Again, from Δ APB, 
If PB = y then cos α = y /AP







