PRINCIPLE OF MATHEMATICAL INDUCTION, PERMUTATION AND COMBINATION
MATHEMATICAL INDUCTION
- In drawing scientific conclusions, there are two fundamental processes of reasoning that are commonly employed. One is the process of deduction, i.e. the process of reasoning from general to particular and the other is known as the process of induction which proceeds from particular to general. The word induction means the method of reasoning about a general statement from the conclusion of particular cases. Induction begins by observations. We observe and use our intuition to arrive at a tentative conclusion called conjecture. It may be true but then it must be so proved by the process of reasoning. Else it may be false but then it must be shown by finding a counterexample where the conjecture fails.
- In algebra or in other disciplines of mathematics, there are certain results or statements that are formulated in terms of n, where n is a positive integer. To prove such statements, well suited method, based on the specific technique, is known as the Principle of Mathematical Induction.
- The Principle of Mathematical Induction is a direct outcome of PEANO'S AXIOMS : which define natural number set N axiomatically.
PEANO'S AXIOMS
For the set of natural numbers N.
P1. There exists a natural number 1.
P2. There exists an injective mapping . If
. If 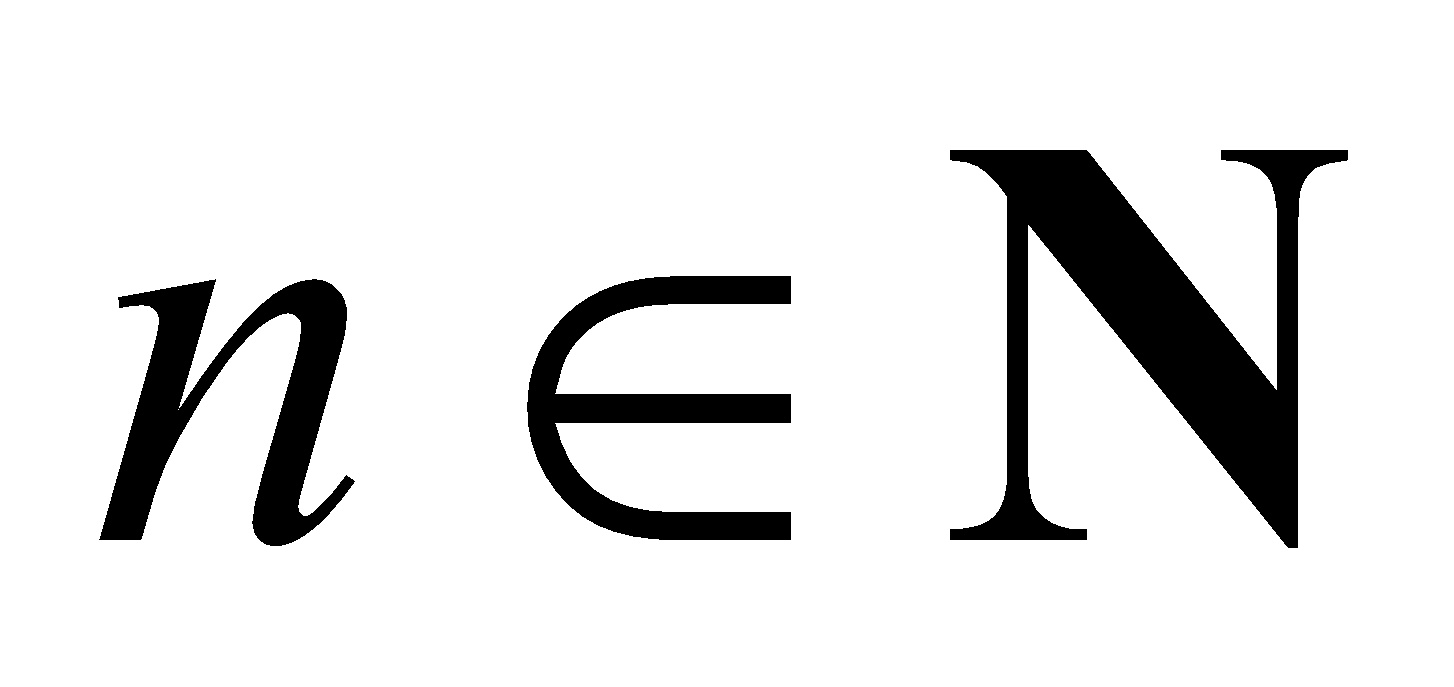 , then σ(n) is called the SUCCESSOR of n. [σ(n) = n + 1].
, then σ(n) is called the SUCCESSOR of n. [σ(n) = n + 1].
P3. The mapping σ is not bijective. In particular .
.
P4. If K be a subset of N, such that 1 ∈ K and n ∈ K
⇒ σ(n) ∈ K, then K = N.
Axiom P4, is commonly known as the axiom of induction.
Axiom P3 asserts that 1 is a non-successor.
Axiom P2 asserts that σ (m) = σ (n)  m = n
m = n
Axiom P1 asserts that  .
.
PRINCIPLE OF MATHEMATICAL INDUCTION
Consider a set K containing natural numbers. If it satisfies the following two conditions :
- For each natural number, it is true that
. Then K = N.
This principle gives three (at least) important propositions.
FIRST PRINCIPLE OF INDUCTION (FPI)
Let {T(n) :  } be a set of statements, one for each natural number n.
} be a set of statements, one for each natural number n.
If T(1) is true and the truth of T(k) implies that of T(k + 1), then T(n) is true for all n.
Example :
Solution :
Let us write the statement 
First we verify that T(1) is true. We note that
Hence T(1) is true
Now let us assume that T(k) is true,
i.e., T(k) : "k3 + (k + 1)3 + (k + 2)3 is divisible by 9". ...(1)
We have to prove that  is true whenever T(k) is true.
is true whenever T(k) is true.
we have 
=  ...(2)
...(2)
From (1),  is divisible by 9. Also 9 (k2 + 3k + 3) is divisible by 9. So expression on the R.H.S. of (2) is divisible by 9.
is divisible by 9. Also 9 (k2 + 3k + 3) is divisible by 9. So expression on the R.H.S. of (2) is divisible by 9.
Thus, T(k + 1) is true whenever T(k) is true. Hence by the First Principle of Mathematical Induction (FPI), the statement
SECOND PRINCIPLE OF INDUCTION (SPI)
Let {T(n) : n ∈ N} be a set of statements, one for each natural number n.
If (i) T(1) is true, and (ii) for each natural number k, the truth of T(m) for all m < k implies the truth of T(k).
Then T(n) is true for all n.
SPI is sometimes called Strong principle of Induction and FPI is then called Weak principle of Induction.
THIRD PRINCIPLE OF INDUCTION (TPI)
Let {T(n) : n ∈ N} be a set of statements, one for each natural number n. If
- T(a) is true for some a ∈ N and
- T(k) is true implies T(k + 1) is true for all. Then T(n) is true for all.
FUNDAMENTAL PRINCIPLES OF COUNTING
- Principle of Addition : If an event can occur in 'm' ways and another event can occur in 'n' ways independent of the first event, then either of the two events can occur in (m + n) ways.
- Principle of Multiplication : If an operation can be performed in 'm' ways and after it has been performed in any one of these ways, a second operation can be performed in 'n' ways, then the two operations in succession can be performed is (m × n) ways.
Example :
In a class there are 10 boys and 8 girls. The class teacher wants to select a student for monitor of the class. In how many ways the class teacher can make this selection ?
Solution :
The teacher can select a student for monitor in two exclusive ways
(i) Select a boy among 10 boys, which can be done in 10 ways OR
(ii) Select a girl among 8 girls, which can be done in 8 ways.
Hence, by the fundamental principle of addition, either a boy or a girl can be selected in 10 + 8 = 18 ways.
Example :
In a class there are 10 boys and 8 girls. The teacher wants to select a boy and a girl to represent the class in a function. In how many ways can the teacher make this selection?
Solution :
The teacher has to perform two jobs :
(i) To select a boy among 10 boys, which can be done in 10 ways.
(ii) To select a girl, among 8 girls, which can be done in 8 ways.
Hence, the required number of ways = 10 × 8 = 80.
Example :
There are 6 multiple choice questions in an examination. How many sequences of answers are possible, if the first three questions have 4 choices each and the next three have 5 choices each?
Solution :
Each of the first three questions can be answered in 4 ways and each of the next three questions can be answered in 5 different ways.
Hence, the required number of different sequences of answers = 4 × 4 × 4 × 5 × 5 × 5 = 8000.
Example :
Five persons entered a lift cabin on the ground floor of an 8-floor house. Suppose that each of them can leave the cabin independently at any floor beginning with the first. What is the total number of ways in which each of the five persons can leave the cabin at any of the 7 floors?
Solution :
Any one of the 5 persons can leave the cabin in 7 ways independent of other.
Hence the required number of ways = 7 × 7 × 7 × 7 × 7 = 75.
NOTATIONS
The Factorial : The continued product of first 'n' natural numbers is called the "n factorial" and is denoted by
n! or
n! or
Thus, 
Obviously, 
Generally, "zero factorial" is defined as 1, i.e., 0! = 1.
The factorials of fractions and negative integers are not defined.
nPr and nCr
If n ∈ N and 'r' is an integer such that  , then we define the following symbols
, then we define the following symbols
- P(n, r) or nPr =
- C(n, r) or nCr =
. The symbol nCr is also denoted by
.
IMPORTANT RESULTS
- If
, then nPs is divisible by nPr.
that is,
and
Example :
Prove that n! + 1 is not divisible by any natural number between 2 and 'n'.
Solution :
Since n! = 1 . 2 . 3 . 4 ..... (n – 1) . n
Therefore n! is divisible by any number from 2 to 'n'.
Consequently n! + 1, when divided by any number between 2 and 'n' leaves 1 as remainder.
Hence, n! + 1 is not divisible by any number between 2 and 'n'.
Example :
What is the largest integer 'n' such that 33! is divisible by 2n?
Solution :
We have
33! 
Thus the maximum value of 'n' for which 33! is divisible by 2n is 31.
METHODS OF SAMPLING
Suppose {x1, x2,....., xn} is a set of 'n' distinct objects from which we want to take a sample of r (1 ≤ r ≤ n) objects. To complete the problem we need the following specifications to be clearly stated :
- Is the order in which we take the sample important or not.
- Is the repetition of the objects allowed or not.
If the order is important, then we say that the sample consists of ARRANGEMENTS. If the order is not important, we have SELECTIONS. If repetition is allowed we have REPLACEMENT.
Thus, our sampling process can be divided into following forms :
- The order is IMPORTANT and the repetition is ALLOWED, each sample is then a SEQUENCE.
- The order is IMPORTANT and the repetition is NOT ALLOWED, each sample is then a PERMUTATION.
- The order is NOT IMPORTANT and repetition is ALLOWED, each sample is then a MULTISET.
- The order is NOT IMPORTANT and repetition is NOT ALLOWED, each sample is then a COMBINATION.
Example :
Let us take out two objects from the set {a, b, c}. The following situations arise as per above theory :
PERMUTATIONS
Each of the arrangements, which can be made by taking, some or all of a number of things is called a PERMUTATION.
RESULT 1 : To find the number of permutations of 'n' things taken 'r' at a Time :
The problem is equivalent to filling 'r' places with 'n' different things.
The first place can be filled in 'n' ways, as any one of the 'n' things may be taken.
Having filled the first place, there remain 'n – 1' things so the second place can be filled in (n – 1) ways.
Hence, first two places can be filled in n (n – 1) ways.
After filling the first two places there are 'n – 2' objects left with to fill the third place, and so on.
Hence, the number of ways of filling 'r' places with 'n' things
= 
The above formula for nPr involves following conditions :
- All the things are distinct.
- Repetition of things is not allowed in any of the arrangements.
- No arrangement is repeated.
- The arrangement is linear.
RESULT 2 : The number of permutations of 'n' things taken all at a time.
This will be given by above formula after taking r = n.
Thus, required number of ways = nPn = n!
RESULT 3 : To find the number of permutations of 'n' things taken all at a time, when 'p' are alike of one kind, 'q' are alike of Second, 'r' alike of Third, and so on :
Let 'x' be the required number of permutations.
If p alike things are replaced by p distinct things, which are also different from others, then without changing the positions of other things these new p-things can be arranged in p! ways.
Each of 'x' permutations will give p! permutations. Thus the total number of permutations now are x (p!)
With a similar argument for 'q' - alike and 'r' - alike things, we get that if all things are different the number of permutations would be x(p!) (q!) (r!)
But number of permutations of 'n' distinct things; taken all at a time = nPn = n!, thus, 
Example :
How many different words can be formed with the letters of the world MISSISSIPPI.
Solution :
In the word MISSISSIPPI, there are 4 I's, 4S's and 2P's.
Thus required number of words = 
RESULT 4 : To find the number of Permutations of 'n' different things, taking 'r' at a time, when each thing can be repeated 'r' times:
In the problem we have to fill 'r' vacant places with 'n' things with repetition. Obviously, each place can be filled in 'n' ways, leaving again n ways for the other place.
Hence, the number of ways of filling r-places with 'n' things = n × n × n × ....... × n (r factors) = nr
Example :
In how many ways can 5 prizes be given away to 4 boys, when each boy is eligible for all the prizes?
Solution :
Any one of the prizes can be given in 4 ways; then any one of the remaining 4 prizes can be given again in 4 ways, since it may even be obtained by the boy who has already received a prizes. Hence 5 prizes can be given 4 × 4 × 4 × 4 × 4 = 45 ways.
Example :
How many numbers of 3 digits can be formed with the digits 1, 2, 3, 4, 5 when digits may be repeated?
Solution :
The unit place can be filled in 5 ways and since the repetitions of digits are allowed, therefore, tenth place can be filled in 5 ways.
Furthermore, the hundredth place can be filled in 5 ways also. Therefore, required number of three digit numbers is 5 × 5 × 5 = 125.
RESULT 5 : Number of circular permutations of 'n' distinct objects :
Suppose the required number of permutations is 'x'. Since each circular permutation corresponds to 'n' linear permutations depending on where (out of the 'n' positions) we start.
Therefore the total number of linear permutations is xn.
But the number of linear permutations is n!.
Therefore, 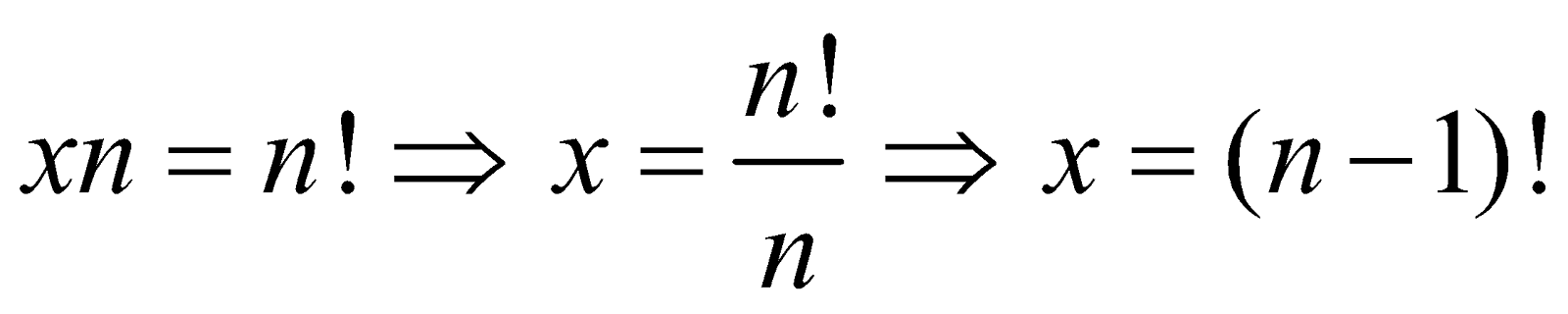
Thus the total number of circular permutations of 'n' distinct things is (n – 1)!.
If no distinction is made between anti-clockwise and clockwise arrangements, then the number of permutations is 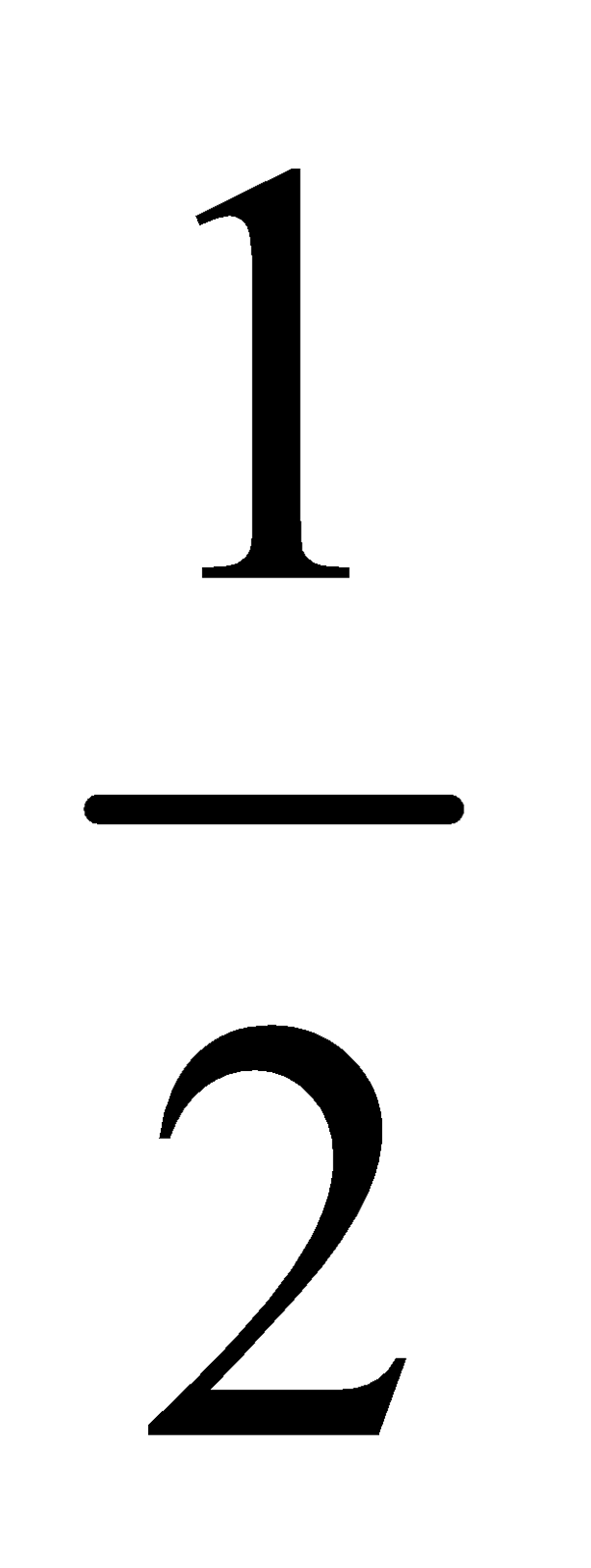 (n – 1)!
(n – 1)!
Example :
In how many ways 8 persons can be arranged in a circle?
Solution :
The eight persons can be arranged in a circle in (8 – 1)! = 7! = 5040.
Example :
Find the number of ways in which 18 different beads can be arranged to form a necklace.
Solution :
18 different beads can be arranged among themselves in a circular order in (18 – 1)! = 17! ways. Now in the case of necklace there is no distinct between clockwise and anticlockwise arrangements. So, the required number of arrangements = 
COMBINATIONS
Each of the selections that can be made with a given number of objects taken some or all of them at a time is called a COMBINATION.
RESULT 1 : To find the number of combinations of 'n' dissimilar things taken 'r' at a time :
Let the required number of selections be 'x'.
Consider one of these 'x' ways. there are 'r' things in this selection which can be permutated in r! ways.
Thus, each of the 'x' selections gives r! permutations. Consequently, the total number of permutations of 'n' things taken 'r' at time is x (r!).
But this number is also nPr.
Thus, the total number of combinations of 'n' dissimilar things taken 'r' at a time is nCr.
The number of combinations of 'n' dissimilar things taken all at a time = nCn = 1.
RESULT 2 : To find the number of Combinations of 'n' different things taking some or all at a time : Out of 'n' things, 1 thing can be selected in nC1 ways; 2 things can be selected in nC2 ways, 3 things can be selected in nC3 ways and so on.
Hence the total number of combinations is
RESULT 3 : The number of selections of some or all out of (p + q + r + ..... ) things out of which p are alike of one kind, q - alike of second kind and so on :
The total number of required ways
= (p + 1) (q + 1) (r + 1) ...... – 1
RESULT 4 : The number of selections of one or more things from 'p' identical things of one kind, 'q' identical things of a second kind, 'r' identical things of a third kind and 'n' different things
The total number of required ways
= (p + 1) (q + 1) (r + 1) 2n – 1
RESULT 5 : The number of ways of dividing 'm + n' things into two groups containing 'm' and 'n' things respectively :
This is equivalent to finding the number of combination of 'm + n' things by taking 'm' at a time. Thus,
The required number of groups = 
If m = n, the groups are equal and in this case the number of different ways of distribution = 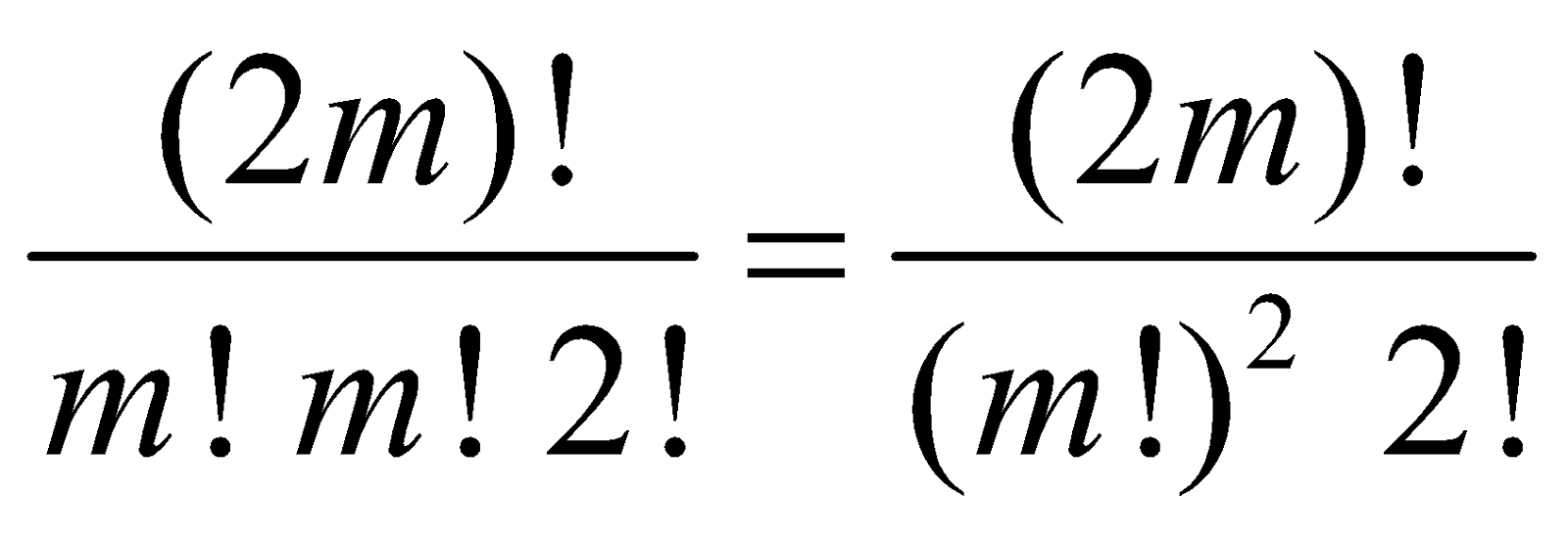
If however, the order of group is important (e.g., 2m things divided equally between two persons), the number of divisions = 
RESULT 6 : The number of ways of dividing m + n + p things into three groups containing m, n and p things respectively :
As in the previous case, the required number is 
If '3m' things are divided into three equal groups then the number of subdivision is 
Buf if '3m' things are to be divided among three persons, then the number of divisions is 
The above results can be easily generalized, that is, mn distinct objects are to be divided into m groups.
If the order of groups is not important 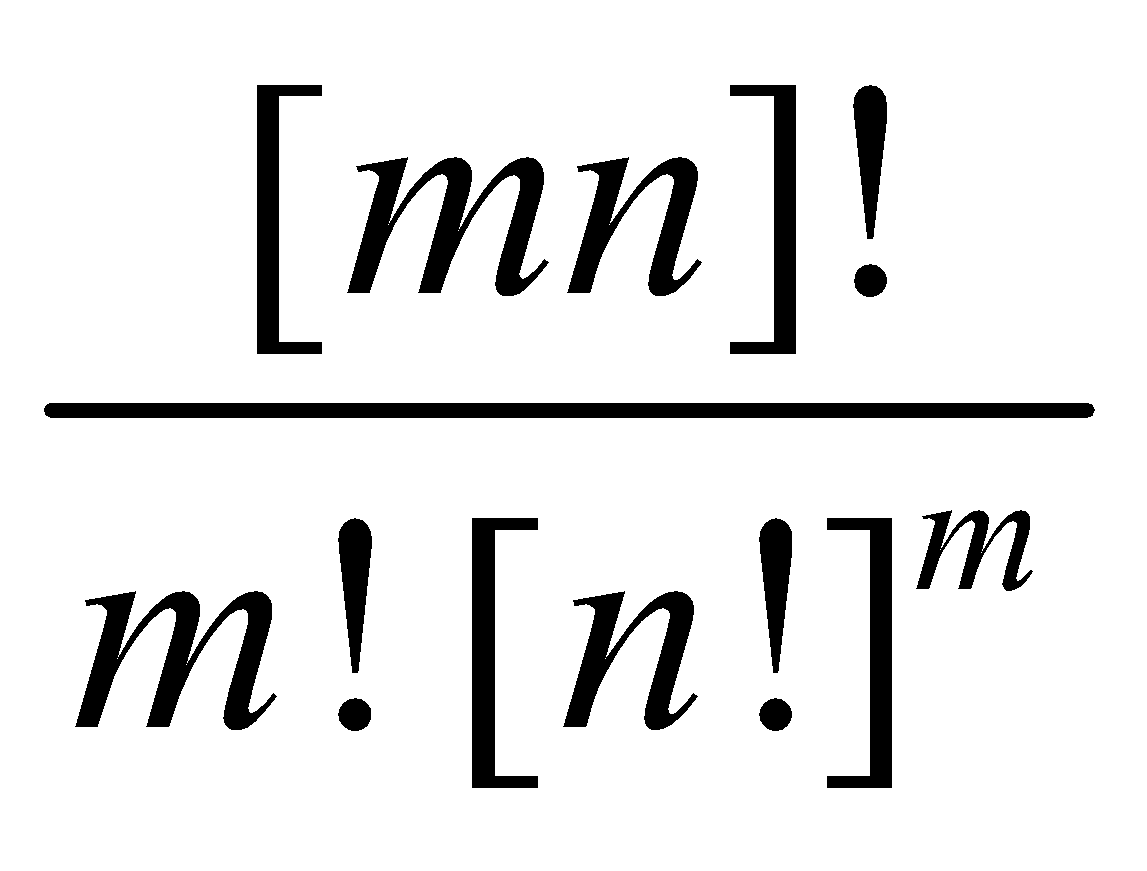 and if the order of groups is important
and if the order of groups is important 
MULTINOMIAL THEOREM
Use of expansion to evaluate number of combination
RESULT 1 : The total number of ways of dividing 'n' identical things among 'r' persons, each of whom can receive 0,1,2 are more ( ) things is
) things is 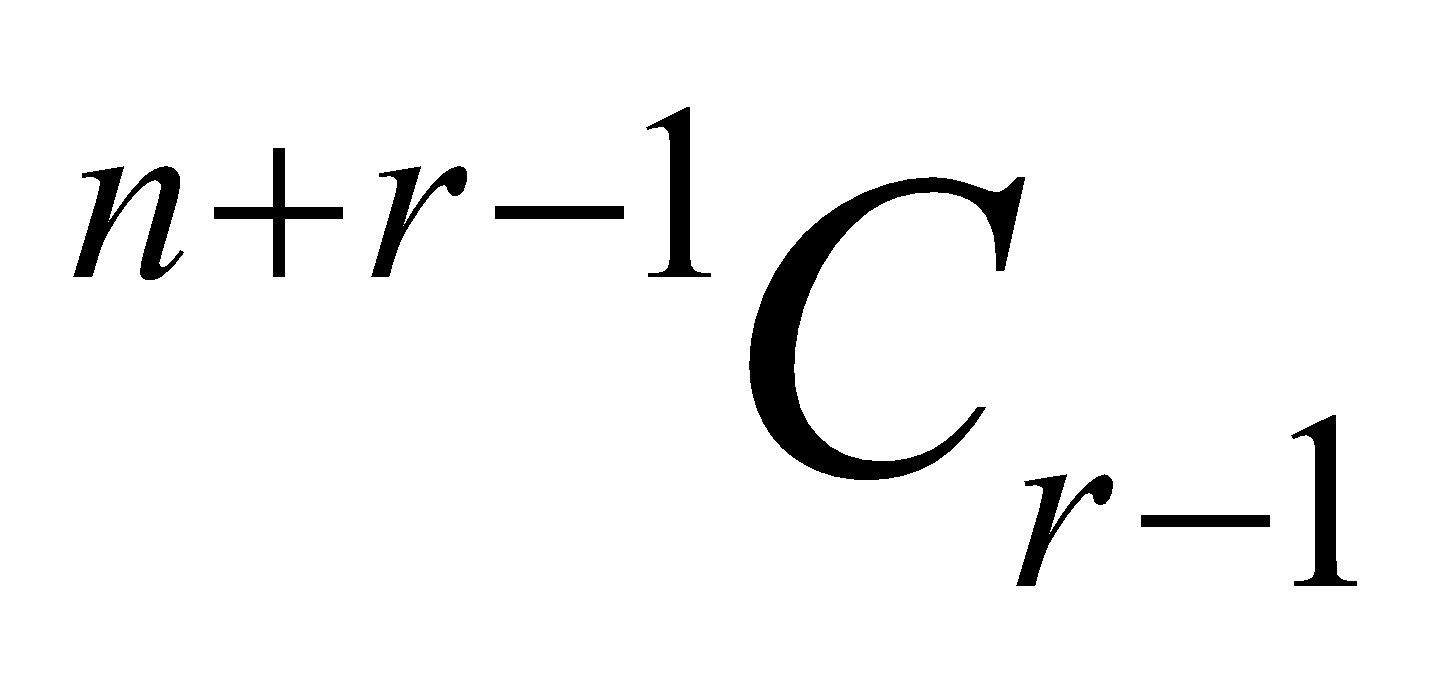 (Alternatively, n identical balls to be distributed in r boxes, when blank box is allowed).
(Alternatively, n identical balls to be distributed in r boxes, when blank box is allowed).
Let us consider 'r' brackets corresponding to 'r' persons.
We take in each bracket an expression given by 1 + x + x2 + .... + xn , where the various powers of x; namely 0, 1, 2, ...., n correspond to the number of things each persons can have in the distribution.
The required number of ways
= coefft. of xn in the product (1 + x + x2 ..... + xn) ( ) ( )...... repeated r times
= coefft xn in  = coefft of xn in
= coefft of xn in
= 
RESULT 2 : The total number of ways to divide 'n' identical things among 'r' persons when each gets at least one thing is = coeff of xn in ( x + x2 + ....+ xn-r+1)r
 = coeff of xn– r in (1 – x)–r
= coeff of xn– r in (1 – x)–r
RESULT 3 : The total number of selections of 'r' things from 'n' things where each thing can be repeated as many times as one can is  .
.
The required number of ways = coefficient of xr in
(1 + x + x2 + .........)n
= coefficient of xr in  coefft. of xr in (1 – x)–n
coefft. of xr in (1 – x)–n
= 
RESULT 4 : Number of ways of dividing n identical things into r groups such that no group contains less than m things and more than k (m < k) things is coefficient of xn in the expansion of (xm + xm + 1 + ..... + xk)r
RESULT 5 : The number of ways of selecting r things out of n things of which p are alike and are of one kind, q are alike and are of second, s are alike and are of third kind and so on, is
= coefficient of xr in
[(1 + x + x2 + ..... + xp) (1 + x + x2 + ..... + xq) × (1 + x + x2 + ..... + xs) .....]
RESULT 6 : The number of ways of selecting r things out of n things of which p are alike and are of one kind, q are alike and are of second kind and rest (n – p – q) things are all different is :
= coefficient of xr in
[(1 + x + x2 + ..... + xp) (1 + x + x2 + ..... + xq) × (1 + x)n – p – q]
RESULT 7 : The number of ways of selecting r things out of n things of which p are alike and are of one kind, q are alike and are of second kind, s are alike and are of third kind when each thing is taken at least once :
= coefficient of xr in
[(x + x2 + ..... + xp) (x + x2 + ..... + xq) × (x + x2 + ..... + xs) .....]
RESULT 8 : The number of non-negative integral solutions of the equation x1 + x2 + ..... + xr = n is n + r – 1Cr.
RESULT 9 : The number of terms in the expansion of (a1 + a2 + a3 + .... + an)r is n + r – 1Cr.
AN IMPORTANT EXPANSION
PRODUCT OF TWO INFINITE POWER SERIES
where  for all
for all  .
.
NUMBER OF RECTANGLES AND SQUARES
- Number of rectangles of any size in a square of size
n × n isand number of squares of any size is
.
- Number of rectangles of any size in a rectangle of size
n × p (n < p) is(n + 1) (p + 1) and number of squares of any size is
.
DEFRAGEMENTS
Any change in the given order of the things is called a DEFRAGEMENT.
If n things form an arrangements in a row, the number of ways in which they can be defragged so that no one of them occupies its original place is
SOME SPECIAL FORMULAE
CONDITIONAL PERMUTATIONS
- Number of permutations of n things taking r at a time, when a particular object is to be always included in each =
- Number of permutations of n things taking r at a time, when a particular object is never taken in any arrangement =
- Number of permutations of n different things taking all at a time, when m specified things always come together
= - Number of permutations of n different things taking all at a time, when m specified things never come together
= - Number of permutations of n different things taking r at a time, in which two specified objects always occur together =
- Number of ways of arranging n objects on a circle taking r at a time
= , if clockwise and anticlockwise arrangements are distinct
, if clockwise and anticlockwise arrangements are distinct
= , if clockwise and anticlockwise arrangements cannot be distinguished.
, if clockwise and anticlockwise arrangements cannot be distinguished.
CONDITIONAL COMBINATIONS
- Number of combinations of n distinct things taking r
at a time, when k
particular objects always occur =
.
- Number of combinations of n distinct objects taking
at a time, when k
particular objects never occur =
.
- Number of selections of r things from n things when p particular things are not together in any selection
= nCr – n – pCr – p - Suppose a number N, is expressed in prime factorisation as following
N = 
where p1, p2, p3, ........, pm are prime integers and are any positive integers. Then
- Total number of all divisors of N =
- Sum of all divisors =
= 
- Number of selection or r consecutive things out of n things in a row = n – r + 1
- Number of selection of r consecutive things out of n things along a circle
= 
- Number of selection of r things (r ≤ n) out of n identical things = 1.
- Number of selection of zero or more things out of n identical things = n + 1.
- Number of selection of one or more things out of n identical things = n.







