Limits, Continuity and Differentiability | Mathematics Notes for IITJEE Main

LIMITS, CONTINUITY AND DIFFERENTIABILITY

LIMIT OF A FUNCTION

FORMAL DEFINITION OF LIMITS

The limit of the function f(x) at x = a will be l if for every ∈>0, but small, we may find δ > 0,

such that 0 < |x – a| < δ ⇒ |f(x) – l | <∈

Symbolically, we write

The definition given above may be stated "as the limit of the function f(x) at x = a will be l if the numerical difference between the values of f(x) and l can be made as small as we please (i.e. approaches to zero), as x approaches a (i.e. the difference of the values of x and a is sufficiently small)".

Students must be clear that at this stage we never use the above definition for the evaluation of limits.

VALUE AND LIMIT OF A FUNCTION

The value of the function f(x) at a point a, i.e. f(a), and the limiting value of the function f(x) as x approaches a, i.e., may be same or may differ. Even, we may come across some functions, which are not defined at a, i.e., a does not belong to their domain but limit can be found out at x = a. On the other hand for some functions f(a) may exist but  may not exist.

UNIQUENESS OF LIMIT

If 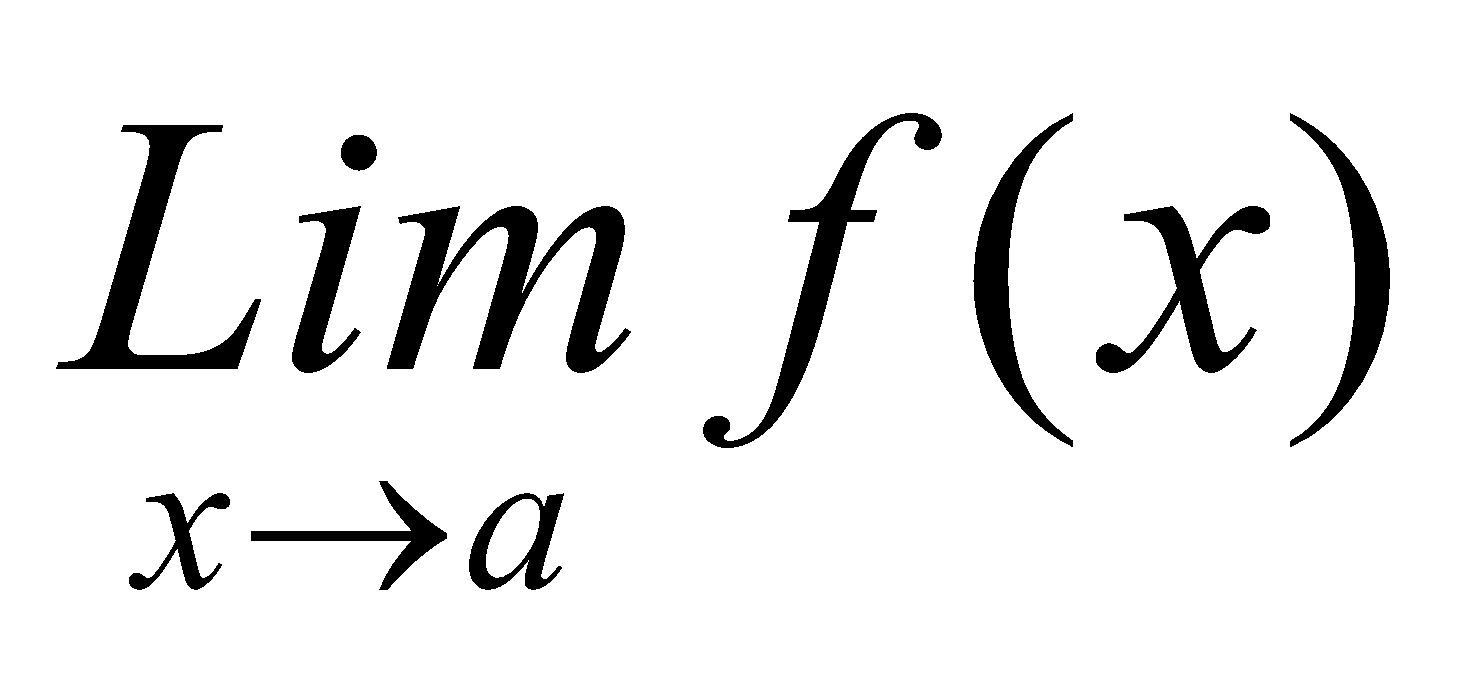  exists, it is unique. There cannot be two distinct numbers l1 and l2 such that when x tends to a, the function f(x) tends to both l1 and 12.

FUNDAMENTAL THEOREMS ON LIMITS

If f(x) and g(x) be two functions of x such that   and both exist, then

1. 
2. where k is a fixed real number.
3. 
4. 
5. if exists
6. if exists
7. provided
8. 

METHODS OF EVALUATING LIMITS

DETERMINATE FORMS

LIMITS BY DIRECT SUBSTITUTION

To find, we  substitute x = a in the function. If the value comes out to be a determinate value, it is the limit. That is,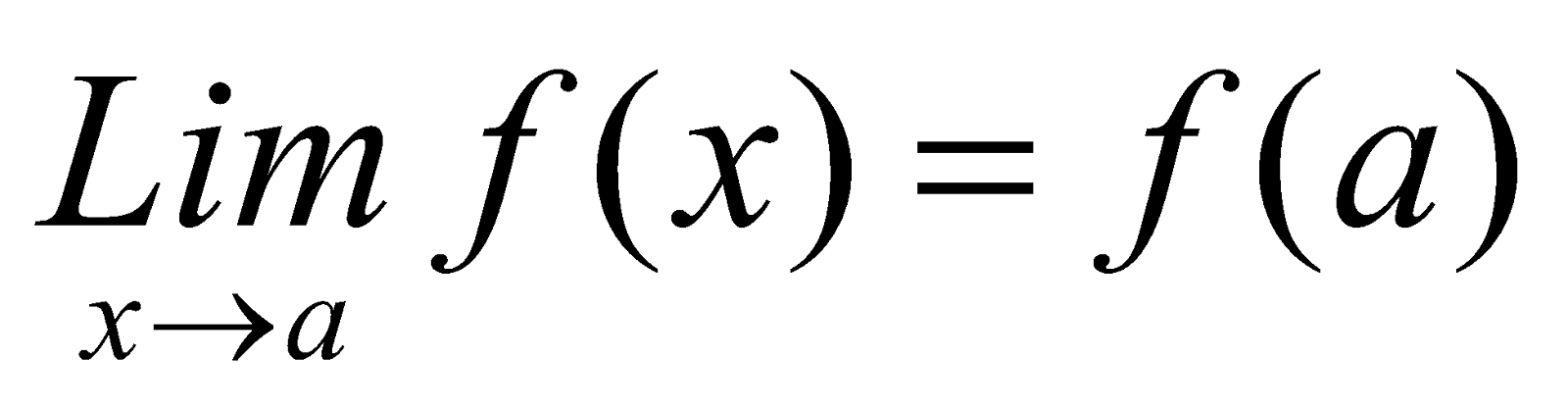provided it exists.

For example,

• 
• 
• 
• 
• 

INDETERMINATE FORMS

If direct substitution of x = a while evaluating leads to one of the following :

Then it is called indeterminate form. We apply special techniques, which are discussed in the next sections :

USE OF L’ HOSPITAL RULE

If  takes the form  then

Note :

• If form then we may repeat the process.
• If the form comes out to be any other indeterminate form, it should be converted to   [see the examples].
• This method makes the evaluation of a limit very easy and may always be used in case of objective type questions. However, if the detail solution is required to be presented (for subjective type problems), L’ Hospital rule must not be used.
• L’Hospital rule is applicable only if the function f(x) and g(x) fulfil certain conditions , which are not given above as such they are not required for the problems we commonly encounter.
• Use L’Hospital rule after learning the differentiation properly.

USE OF STANDARD FORMULAE

1. Algebraic Limits

• 
• 
• 

Remark : Limit in (c) in general right hand limits (i.e for x > 0)

• 
• 
• 
• 

2. Trigonometric Limits

• , x in radian
• ,  x in radian
• 
• 

3. Exponential Limits

• 
• 
• 
• 
• 

4. Logarithmic Limits

LIMITS BY FACTORISATION

If    form, then x – a must be a factor of numerator and denominator which can be cancelled out.

For example :

It is form, hence (x – 2) must be a factor of numerator as well as denominator

LIMITS BY SUBSTITUTION

In order to evaluate   we may, substitute x = a + h or a – h, so  that as x → a, h → 0

Thus

This method is applied to bring the limit at zero as the most of the formulae are given as

For example :

Put  x – 10 = h,  ∴ as x10 , h0

∴ The limit is

LIMITS OF FUNCTIONS AS X ∞

•  is of the form   and f(x) and g(x) are both polynomials of x.

We divide numerator and denominator by the highest power of x and put 0 for

For example,

[ ∞ – ∞ form]

=     [After rationalisation]

[Dividing numerator and denominator by x]

• 

For example,

LIMITS USING EXPANSION

Many limits can be evaluated very easily by applying expansion series. Some of the standard expansions are

1. (1+x)n = 1 +nC1x + nC2x2 + .......+ nCnxn,  
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 

For example,

AN IMPORTANT FORMULA FOR EVALUATING LIMITS OF 1∞ FORMS

where

For example,

   

[Applying L’Hospital rule we may use series for sin x also]

SANDWICH THEOREM

Let f , g, h be three functions such that f ≤ g ≤ h in an open interval containing a. Suppose that  exist and both are equal to l. Then also exists and is equal to the same l.

For example

• holds for all x

Also

• Let it is given that

Then

EXISTENCE OF LIMIT

Consider a function f(x), whose limit as x approaches a is being evaluated. When we state that x is approaching a then x is never equal to a. Rather x is either somewhat less than a and we say that x approaches a from left, or x is somewhat greater than a and we say that x approaches a from right.

These two tendencies can be represented on the real number line as shown below.

x approaches a from left         x approaches a from right

or x∈(a – δ, a), δ > 0         or x∈(a, a + δ), δ > 0

LEFT HAND LIMIT AND RIGHT HAND LIMIT

1. When x tends towards a from the left (i.e. the values of x always remaining somewhat less than a), the value towards which f(x) tends is called the LEFT HAND LIMIT of f(x) at x = a. Symbolically, we write

2. When x tends towards a from the right (i.e. the values of x always remaining somewhat greater than a), the value towards which f(x) tends is called the RIGHT HAND LIMIT  of f(x) at x = a. Symbolically, we write

CONDITION FOR EXISTENCE OF LIMIT

1. If the left hand limit (LHL) and the the right hand limit (RHL) exist at a point and are equal then we conclude that the limit of the function exists at that point.

If . Then

2. If LHL and RHL at a point exist but are not equal, then we conclude that the limit of the function does not exist at that point.

If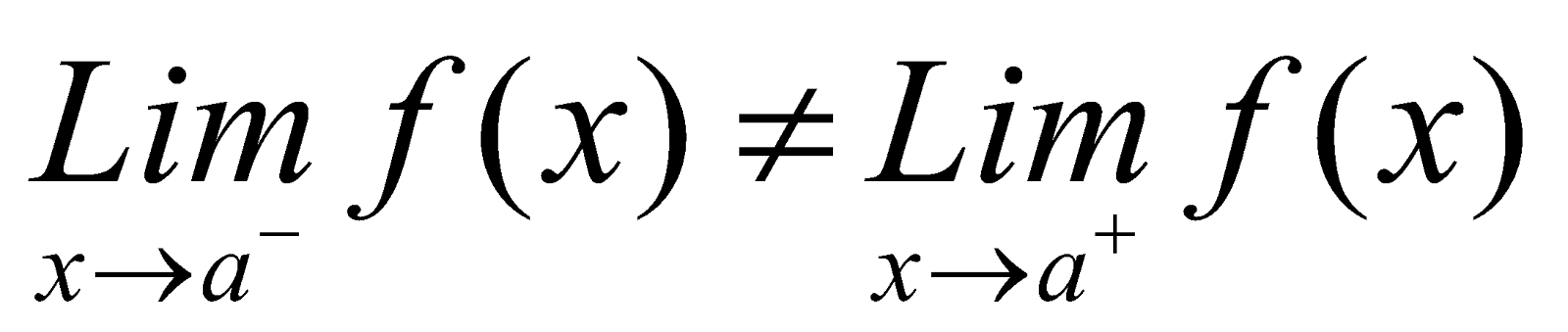 . Then does not exist.

3. In many functions LHL or RHL or both may not exist. For example has neither LHL or RHL at x = 0, because as x approaches 0, f(x) does not approach to any definite value. Actually any interval containing 0, contains infinite cycles.

EVALUATION OF LHL AND RHL

Thus, to find left hand limit at x = a, we replace x by a – h in the function and evaluate the limit at h = 0

Thus, to find right hand limit at x = a, we replace x by a + h in the function and evaluate the limit at h = 0.

For example : Let f(x) = [x] and the limit point be x = 0

  [since –h < 0 ⇒ [–h] = –1]

[Since h > 0 ⇒ [h] = 0

We note that LHL = –1 and RHL = 0, which are not equal, hencedoes not exist.

CAUTION

Never do like this  [– h] = [0] = 0

That is limit must be applied only after removing [] sign.

The limits evaluated earlier were not checked for LHL and RHL because it was assumed already that the limit of those functions exist. Actually, for the algebraic and transcendental functions we encounter, the limits exist. Mostly those functions, which are piecewise defined or composite functions need to be tested for LHL and RHL, specially at those points, where the definition of the function is changing.

CONTINUITY

Geometrically, a function f(x) is said to be continuous in an interval if its graph y = f(x) is a continuous curve in that interval.

CAUCHY'S DEFINITION

Let f be a real function and a be in the domain of f. We say f is continuous at a, if

Hence f(x) is continuous if exists and equals f (a).

The function f(x) is said to be continuous at x = a from left if

The function f(x) is said to be continuous at x = a from right if

DISCONTINUITY OF A FUNCTION

A function f(x), which is not continuous at a point x = a, is said to be discontinuous at x = a.

The function f(x) can be discontinuous at a point x = a in any one of the following ways.

1. f(a) is not defined
2. Either   or both non existing or infinite
3. LHL and RHL both exist but unequal, i.e.

4. LHL and RHL both exist and equal but not equal to f(a), i.e.,

This particular kind is called REMOVABLE DISCONTINUITY

CONTINUITY OF A FUNCTION IN AN INTERVAL

1. A function f(x) is said to be continuous in an open interval (a, b), if f(x) is continuous at every point of the interval.
2. A function f(x) is said to be continuous in a closed interval [a, b]  if f(x) is continuous in (a, b). In addition f(x) is continuous at x = a from right and f(x) is continuous at x =b from left.

FUNDAMENTAL THEOREMS ON CONTINUITY

1. If f and g are continuous functions, then
1. f ± g, fg are continuous
2. cf is continuous, c is a constant
3. is continuous at those points where g(x) ≠ 0.
2. If g is continuous at a point ‘a’ and f is continuous at g(a), then fog is continuous at a.
3. If f is continuous in [a, b], then it is bounded in [a, b] i.e., there exist m and M such that

m and M are called minimum and maximum values of f(x) respectively in the interval [a b]

4. If f is continuous in [a, b], then f assumes at least once every values between minimum and maximum values of f(x)

Thus or range of

f(x) = [m,  M] if x∈[a b]

SOME CONTINUOUS FUNCTIONS

1. Every constant function is continuous at all points
2. The identity function in continuous at all points
3. Every polynomial function is continuous at all points
4. f(x) = sin x and f(x) = cos x are continuous at all points
5. f(x) = ax, a > 0, a ≠ 1 is continuous at all points
6. Rational function is continuous at all points in its domain that is  is continuous at all points, where g(x) ≠ 0, f and g are polynomials.
7. f(x) = log x is continuous if x > 0
8. f(x) = tan x and f(x) = sec (x) are continuous at all points provided
9. f(x) = cot x and f(x) = cosec x are continuous at all points provided .
10. f(x) = | x – a | is continuous at all points.
11. f(x) = [x] is continuous at all points except x∈ I.

DIFFERENTIABILITY (OR DERIVABILITY) OF A FUNCTION

A function f (x) is said to be differentiable at a point 'a' in its domain, if the limit 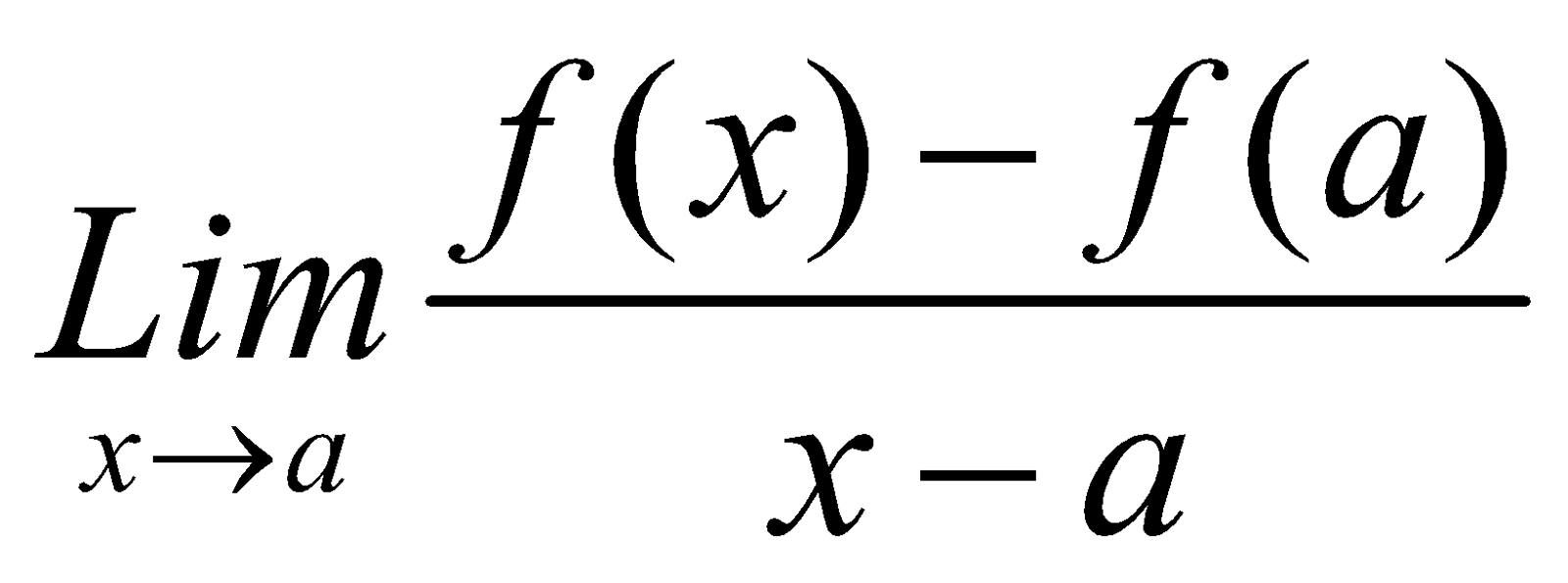  exists finitely. If this limit exists, it is called the derivative of f (x) at x = a, symbolically denoted by f’ (a) or D f (a).

Hence, the function f (x) is differentiable at x = a

if and only if exists finitely

that is, if and only if

If the left hand limit 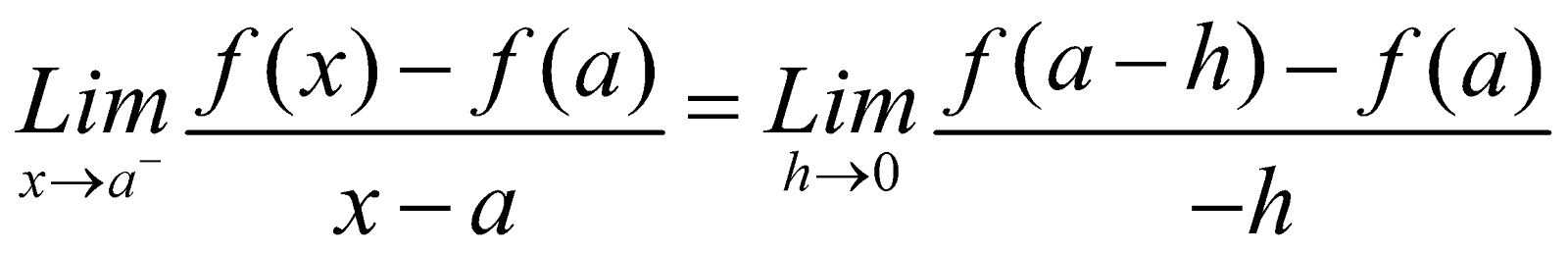, h > 0 exists finitely, it is called Left Hand Derivative (LHD) at x = a and symbolically denoted by Lf’ (a) or f’ (a–) or f’(a – 0) or LDf(a).

If the right hand limit exists finitely, it is called Right Hand Derivative (RHD) at x = a and symbolically denoted by Rf’ (a) or f’(a+) or f’(a + 0) or RDf(a)

For example : Let us check the differentiability of f (x) = |x| at x = 0

.

[As h > 0, ∴ |h| = | –h| = h]

Thus, LHD ≠ RHD. Hence, f(x) = |x| is not differentiable at x = 0.

DIFFERENTIABILITY IN AN INTERVAL

A function f (x) is said to be differentiable in an interval (a, b) if f (x) is differentiable at every point of this interval (a, b).

A function f (x) is said to be differentiable in a closed interval [a, b], if f (x) is differentiable in (a, b), in addition f (x) is differentiable at x = a from right and differentiable at x = b from left.

RELATION BETWEEN CONTINUITY AND DIFFERENTIABILITY

1. If a function f (x) is differentiable at x = a then f (x) is necessarily continuous at x = a.
2. Converse of (1) is not necessarily true. That is, if a function f (x) is continuous at x = a, it is not necessarily differentiable at x = a. For example, f (x) = |x| is continuous at x = 0 but not differentiable at x = 0.
3. If f (x) is not continuous at x = a, then f (x) is not differentiable at x = a.

GEOMETRICAL MEANING OF DIFFERENTIABILITY

Let  y = f (x) be a function and 'a' be a point in the domain. Let P be the point (a, f (a)) on the curve. Let Q (x, f(x)) be an arbitrary point on the curve then the expression represents the slope of the secant joining P and Q.

Thus, the slope of secant joining

As we take the limit x → a, the point M approaches to N. That is the point Q approaches to P. At the limiting case, when Q is infinitesimally close to P, the chord PQ becomes a tangent

(slope of chord PQ) = Slope of tangent at P (a, f (a))

∴ f’(a) represents the slope of tangent at the point x = a

If a function is not differentiable at x = a, then either the tangent at x = a is vertical or the curve has no unique tangent at x = a, i.e., f (x) has a corner at x = a.

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT