Quadratic Equations | Mathematics Notes for IITJEE Main

QUADRATIC EQUATIONS

QUADRATIC EQUATION

A quadratic equation can be expressed as

ax2 + bx + c = 0, a ≠ 0     ...(1)

Where a, b and c are complex numbers

The expression f(x) = ax2 + bx + c,  is called a quadratic trinomial expression.

ROOTS OF A QUADRATIC EQUATION

• The values of x, which satisfy the above written equation (1) are called the roots of the quadratic equation.

A quadratic equation has two and only two roots.

• The roots of the quadratic equation (1) can be evaluated using the following formula.

...(2)

The above formula provides both the roots of the quadratic equation, which are generally denoted by α and β,

say and

QUADRATIC EQUATIONS WITH REAL COEFFICIENTS

Consider the quadratic equation

Where, a, b, and c are real number

The formula is applicable to solve any kind of quadratic equation whether it has real coefficients or complex coefficients, However, onwards we will strictly discuss only those equations, which have real coefficients unless stated otherwise.

The expression inside the square root  is called the DISCRIMINANT of the quadratic equation and denoted by D. Thus, Discriminant (D) = b2 – 4ac.

NATURE OF ROOTS

The nature of roots of the equation depends upon the nature of its discriminant D.

1. If D < 0, then the roots are non-real complex, Such roots are always conjugate to one another. That is, if one root is p + iq then other is p – iq, q ≠ 0.
2. If D = 0, then the roots are real and equal. Each root of the equation becomes . Equal roots are referred as repeated roots or double roots also.
3. If D > 0 then the roots are real and unequal.
4. In particular, if a, b, c are rational number, D > 0 and D is a perfect square, then the roots of the equation are rational number and unequal.
5. If a, b, c, are rational number, D > 0 but D is not a perfect square of a rational number, then the roots of the equation are irrational (surd). Surd roots are always conjugate to one another, that is if one root is . then the other is , q > 0.
6. If a = 1, b and c are integers, D > 0 and  perfect square, then the roots of the equation are integers.

IMPORTANT RESULT

1. The condition that the roots of a quadratic equation are real is  i.e.
2. The quadratic trinomial  will be a perfect square if D = 0 i.e.
3. If is a repeated root of the quadratic equation then is a root of equation as well.
4. If a, b, c are non real and the quadratic equation has non-real roots, then the roots  need not be conjugate.
5. If a, b, c are irrational and the quadratic equation has irrational roots, then the roots are not necessarily conjugate.
6. If a + b + c = 0 then one root is always unity and the other root is , Hence the roots are rational provided a, b, c, are rational.

SIGN OF ROOTS

Let α, β are real roots of the quadratic equation that is D = . Then

1. Both the roots are positive if a and c have the same sign and the sign of b is opposite.
2. Both the roots are negative if a, b and c all have the same sign.
3. The Roots have opposite sign if sign of a and c are opposite.
4. The Roots are equal in magnitude and opposite in sign if b = 0 [ that is its roots are α and –α]
5. The roots are reciprocal if a = c. [i.e., the roots are α and ]
6. If c = 0. then one root is zero
7. If b = c = 0, then both the roots are zero.
8. If a = 0, then one root is infinite
9. If a = b = 0, then both the roots are infinite
10. If a = b = c = 0, then the equation becomes an identity

IMPORTANT RESULTS

1. If a and b have the same sign then the real part of roots is negative (if no restriction is given on D)
2. If a and b have opposite sign then the real part of roots is positive (if no restriction is given on D)
3. If a and c have opposite sign then the roots of the equation are always real.
4. To find a quadratic equation which has roots –α, –β, replace x by –x.
5. To find a quadratic equation which has roots and replace x by .
6. If we replace x by x2, the resulting equation has four degrees and its roots are α, –α, β,–β,
7. If a quadratic equation has more than two roots then it must be an identity.

SYMMETRIC FUNCTIONS OF ROOTS

An expression in α, β is called a symmetric function of α, β if the function is not affected by interchanging α and β. If α, β are the roots of the quadratic equation then,

Sum of roots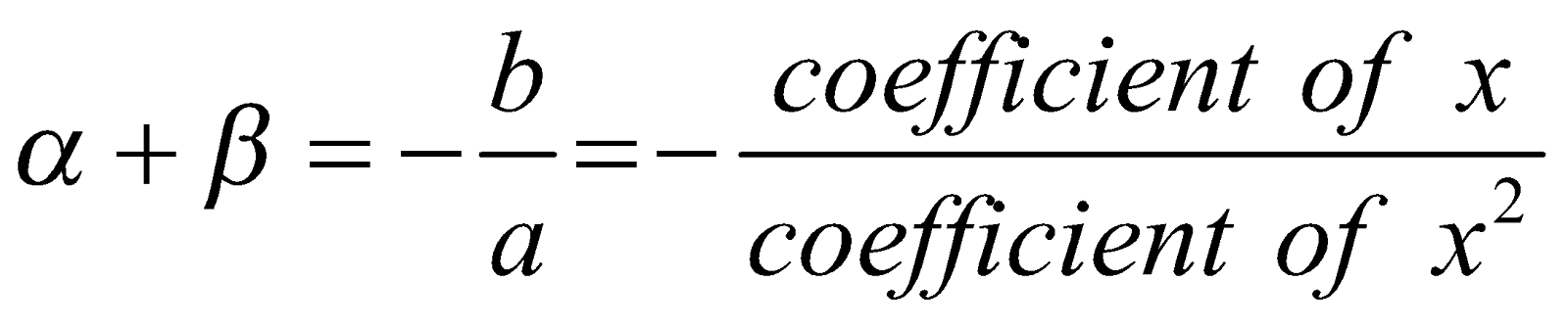   

Product of roots

Note :

1. Above relations hold for any quadratic equation whether the coefficients are real or nonreal complex.
2. With the help of above relations many other symmetric functions of α and β can be expressed in terms of the coefficients a, b and c.
3. Recurrence Relation

4. Some symmetric functions of roots are
1. 
2. 
3. 
4. 
5. 
6. 
7. 

The relations (ii) (iii), (v) and (vii) are not symmetric functions.

FORMATION OF QUADRATIC EQUATION WITH GIVEN ROOTS

• An equation whose roots are α and β can be written as  (x – α) (x – β) = 0 or x2 – (α + β) x + αβ = 0  or x2 – (sum of the roots) x +  product of the roots = 0.
• Further if α and β are the roots of a quadratic equation ax2 + bx + c = 0, then

ax2 + bx + c = a(x – α) (x – β) is an identity.

A number of relations between the roots can be derived using this identity by substituting suitable values of x real or imaginary.

CONDITION OF A COMMON ROOT BETWEEN TWO QUADRATIC EQUATIONS

Consider two quadratic equations

...(i)

and ...(ii)

Let α is a common root of the two equations

Then and

On solving we get

or

Which gives the common root as well as the condition for common root.

CONDITION THAT TWO QUADRATIC EQUATIONS HAVE BOTH THE ROOTS COMMON

Suppose that the equations 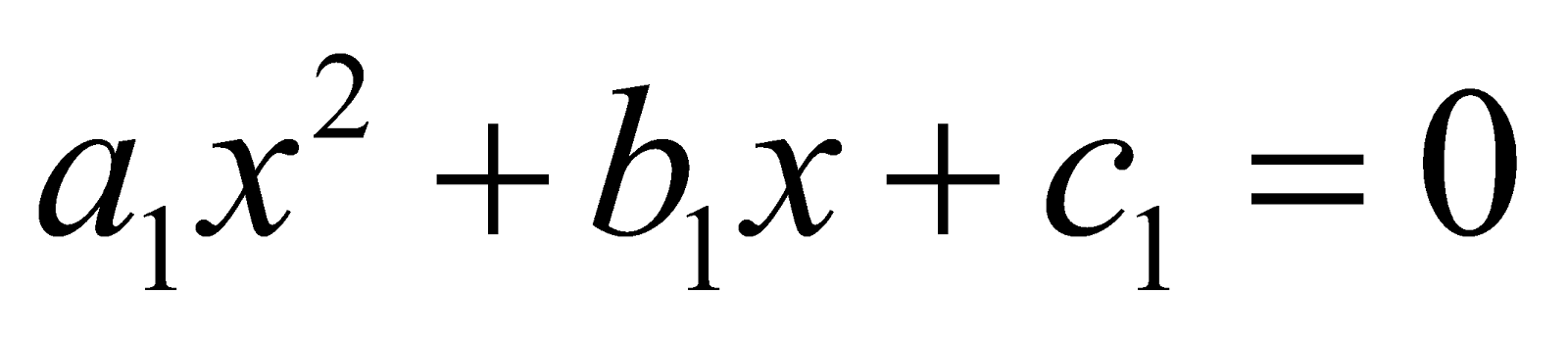and have both the roots common.

then  

If the coefficients of two quadratic equations  are rational (real) and they have one irrational  (imaginary) root common then they must have both the roots common as such roots occur in conjugate pair.

IMPORTANT RESULTS

1. To find the common root of two equations, make the coefficient of second degree terms in two equations equal and subtract. The value of x so obtained is the required common root.
2. If two quadratic equations with real coefficients have an imaginary root common, then both roots will be common and the two equations will be identical. The required condition is :

3. If two quadratic equations with rational coefficient have an irrational root common, then both roots will be common and the two equations will be identical. The required condition is :

4. If α is repeated common root of two quadratic equations f(x) = 0 and, then α is also a common root of the equation f'(x) = 0 and .
5. Previous four articles are applicable for any kind of quadratic equation whether coefficients are real or nonreal complex.

EQUATIONS REDUCIBLE TO QUADRATIC FORM

There are certain equations which are not quadratic equations but can be converted to quadratic equations

FORM 1 : Equations of the form

Procedure :

(i) Put f(x) = y and resulting equation becomes

ay2 + by + c = 0, a quadratic equation

(ii) Solve the quadratic equation by usual method to get two values of y.

(iii) Resubstitute y = f(x) and find x.

FORM 2 : Equations of the form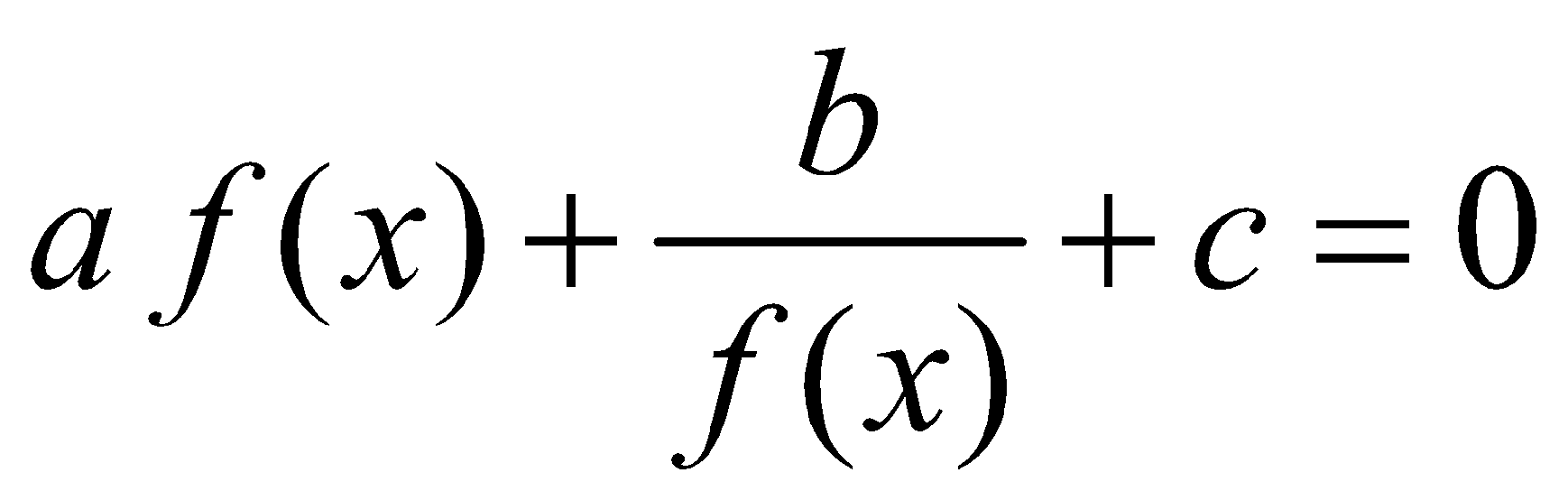

Procedure :
Put f(x) = y and resulting equation becomes , a quadratic equation. where y = f(x) ≠ 0

FORM 3 : Equations of the form apx + bqx + c = 0, where pq = 1

Procedure : Put px = y  then and the resulting equation becomes  

, a quadratic equation, in which y = px  > 0

FORM 4 : Equations of the form apx + bqx + crx = 0, where p, q, r, form a G.P. i.e.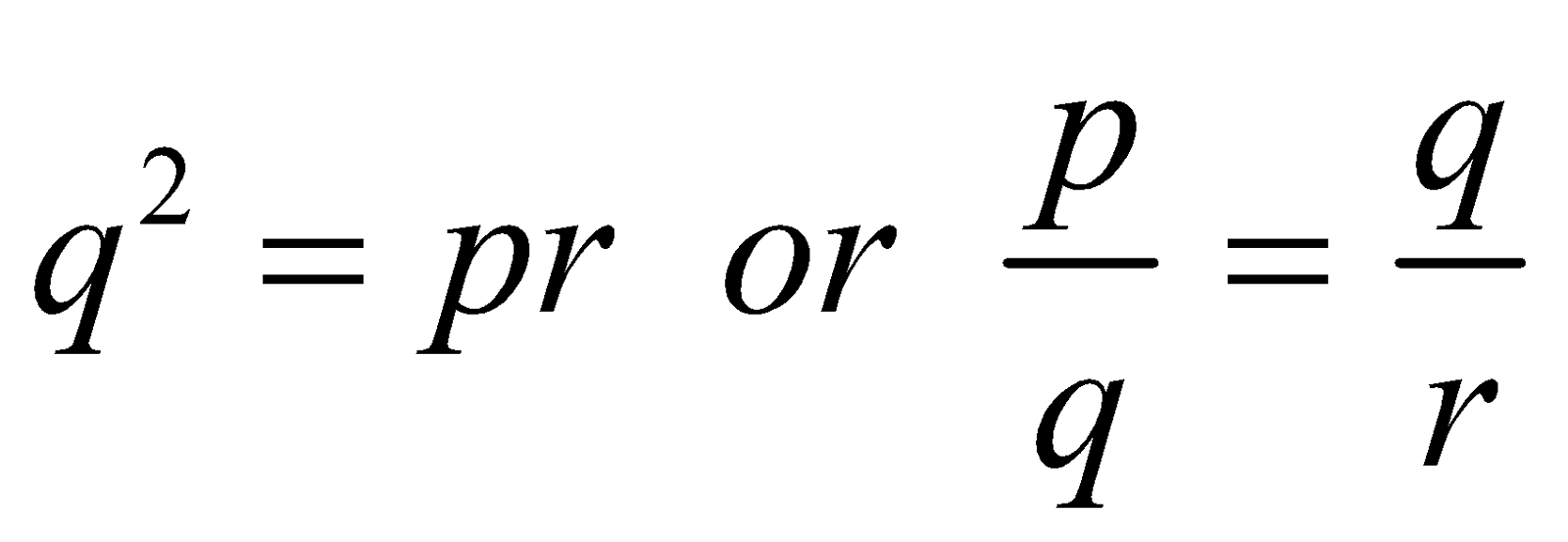

Procedure :

(i) Divide the equation by qx, we get

(ii) Put 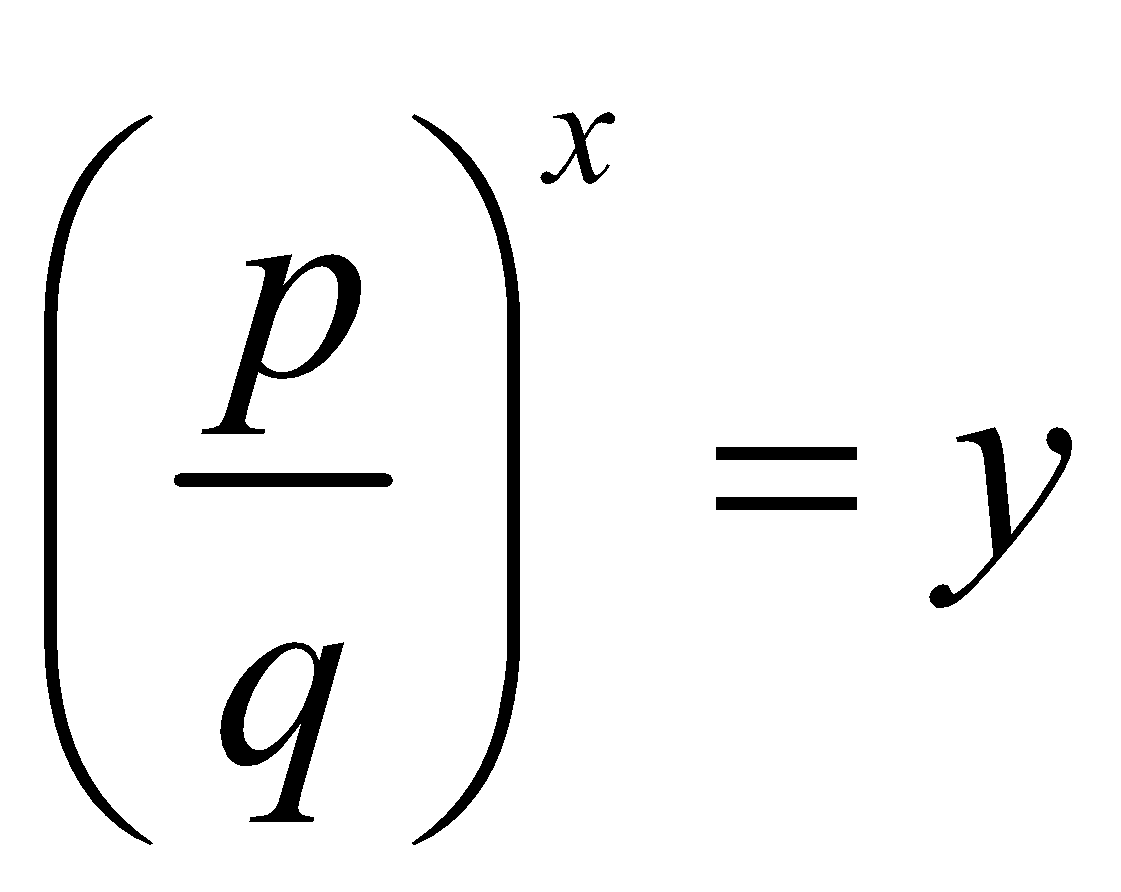then and the resulting equation is, a quadratic equation.

FORM 5 : Equation of the form  (x + a)(x + b)(x + c)(x + d) = k, where a +b = c + d.

Procedure :

Expand the equation in pairs as following :

for a + b = c + d

Let x2 + (a + b)x = y and the equation reduces to (y + ab)(y + cd) = k, a quadratic equation

FORM 6 : Equation of the form (x + a)(x + b)(x + c)(x+d) = kx2, where ab  = cd

Procedure :

Expand the equation in pairs as following

,  for ab = cd

Divide both the sides by x2, we get

Let and the equation reduces to  (y +a + b)(y + c + d) = k, a quadratic equation

FORM 7 : Reciprocal Equations ax4 ± bx3 + cx2 ± bx + a = 0 [Reciprocal equations have equal coefficients in terms equidistant from beginning and end]

Procedure : Divide both the side by x2 ,we get

Put such that or 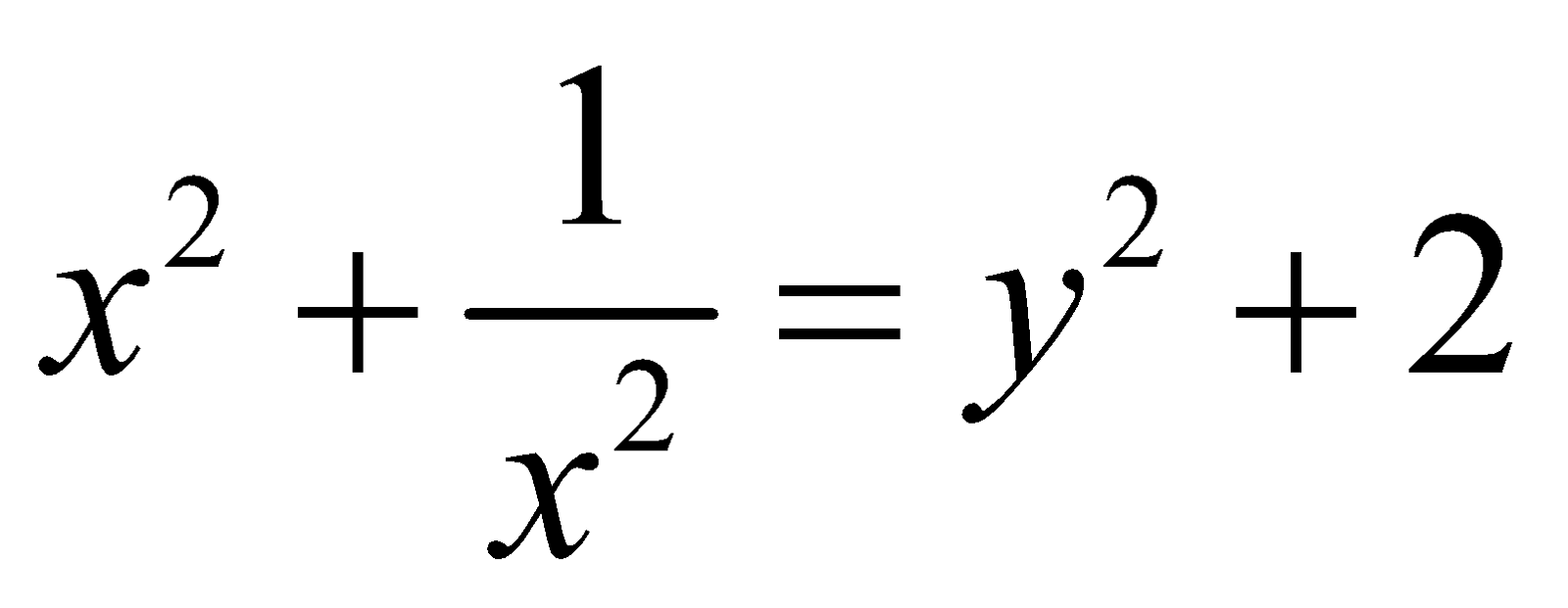respectively.

On substitution the original equation reduces to quadratic equation.

FORM 8 : Equation of the form where

Procedure : Put  

  

and

We get

On expanding it transforms to a quadratic in y2.

Note : In all of the above forms, after substitution the domain of equation often changes, so care must be taken to eliminate erroneous roots or inclusion of missing roots if any.

ANALYSIS OF QUADRATIC TRINOMIAL

Let . We may write

,

where 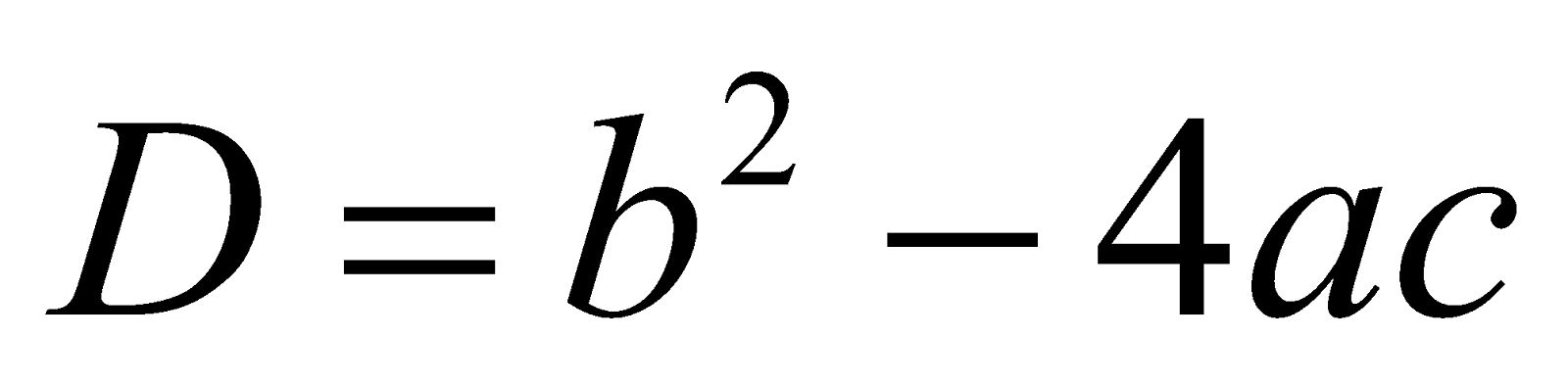is the discriminant of the quadratic.

The equation  represents a parabola, whose axis is parallel to the y-axis and vertex lies at

CASE 1 : If a > 0, the parabola will be concave upward. The position of vertex depends on sign of discriminant D.

• Let D < 0, then vertex lies above  the x -axis.

• Let D = 0 then the vertex lies upon the x-axis.

Actually

and

• Let D > 0, then the vertex lies below the x-axis, hence, the parabola cuts x-axis at two points and , where and represent roots of Then,
  f(x) > 0 if  and if

• In each of the above three situations, the minimum value of is , or the range of value of  is

CASE 2 : If a < 0, the parabola 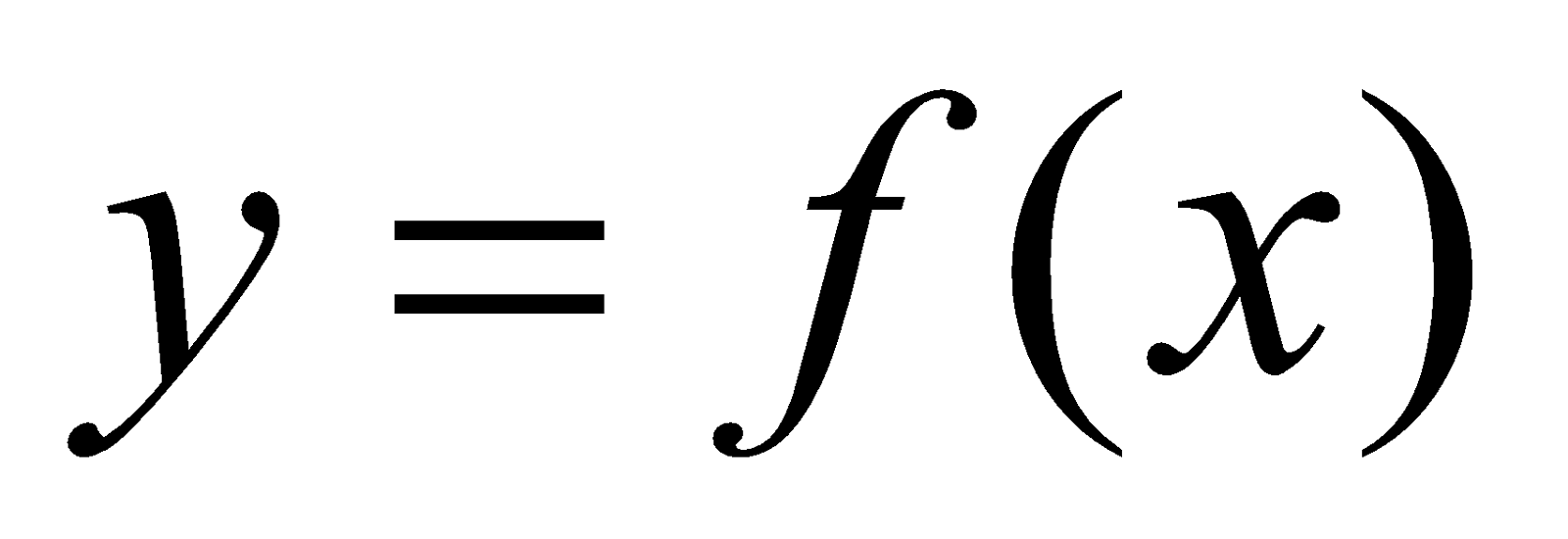will be convex upward. The position of vertex again depends on sign of discriminant D

• Let D< 0, then vertex lies below the x-axis.

• Let D = 0, then vertex lies upon the x-axis

Actually

and

• Let D > 0, then vertex lies above the x-axis, hence, the parabola cuts x-axis in two points and , where and  represent the roots of then,

f(x) > 0, if and

• In each of the above three situations, the maximum value of is , or the range of values of f(x) is .

The above analysis will be applied for the problems of the following types :

PROBLEMS RELATED TO SIGN OF QUADRATICS

From the above analysis, we conclude that

1. If then

For example :

The quadratic

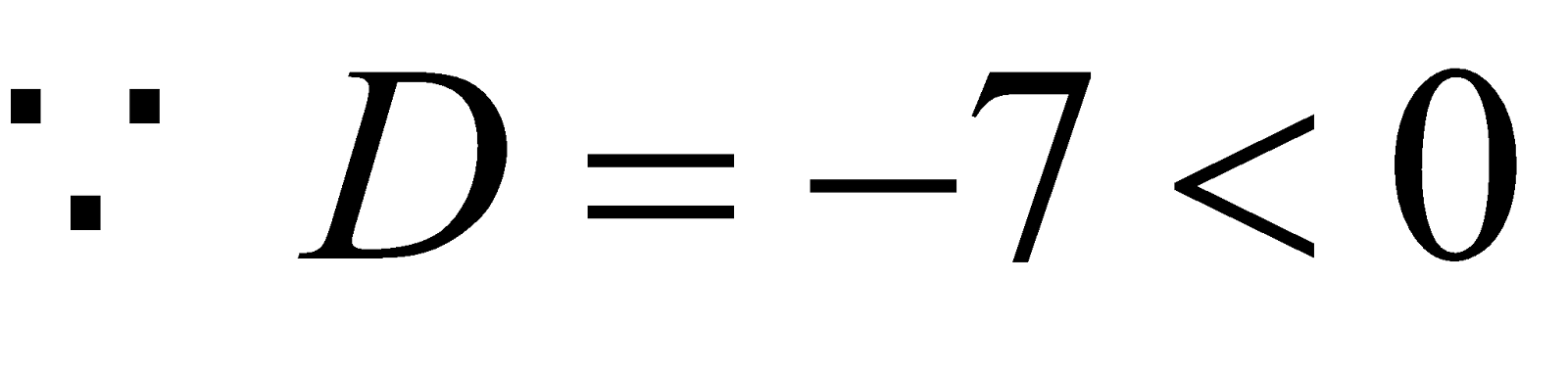
The quadratic and a = –1

2. If  D = 0, then

For example :

and a = 1

Actually and , if x =1

 and a = – 4 < 0

3. If D > 0, then , if and if , where and are the roots of ;

For example :

1. if  x < –1 or x > 2 i.e and if i.e

Here D = 9 > 0  and a = 1 and roots of x2 – x –  2 = 0 are –1 and 2

2. if or and if or

or
Here D = 25 > 0 and a = –6  and roots of are and

4. The quadratic ax2 + bx + c is  positive definite (i.e., always positive) if D < 0 and a > 0

The quadratic ax2 + (2a – 1) x + a + 4 is always positive if and

The common values in and are  

5. The quadratic ax2 + bx + c is negative definite (i.e always negative) if D < 0 and a < 0.

For example :

1. The quadratic is always negative if a < 0 and

The common values of a < 0 and do not exist.

2. The quadratic isalways negative if  

and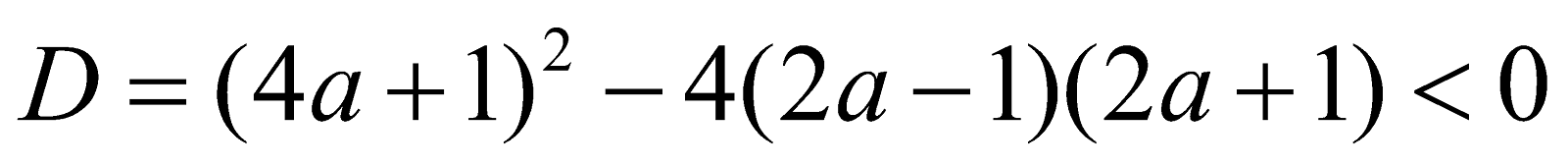

The common values of 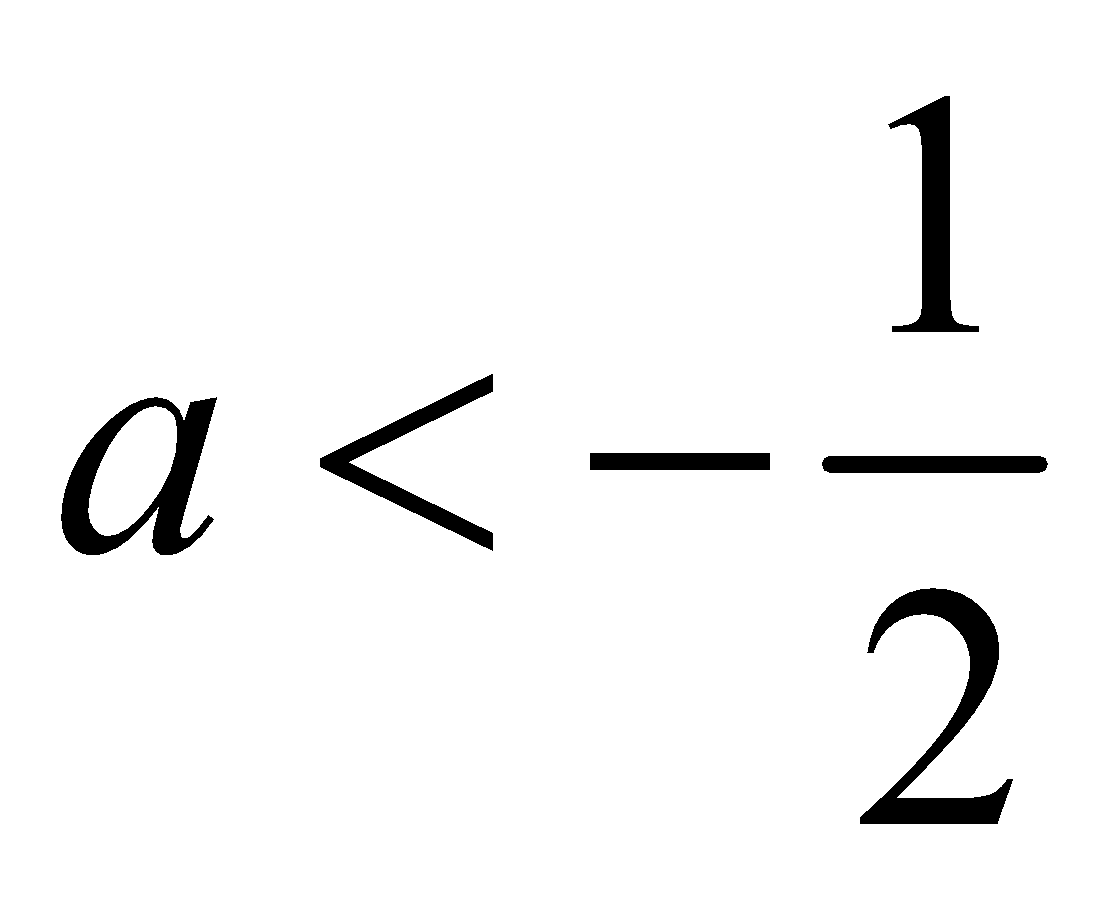and

6. In case, the conditions are required for the quadratic to be always non-negative or non-positive in above (d) and (e), we replace the condition D < 0 by in each case.

PROBLEMS RELATED TO SOLUTIONS OF QUADRATIC INEQUATIONS

From the analysis of quadratic trinomial ax2 + bx + c  we can derive following procedure for the solutions of inequations of the type ax2 + bx + c > 0; ax2 + bx + c < 0; ; .

1. Convert sign of ‘a’ positive by multiplying the inequation by –1. For example, is converted to
2. Evaluate discriminant

If  D < 0, then

i.e for any x.

If D = 0, then

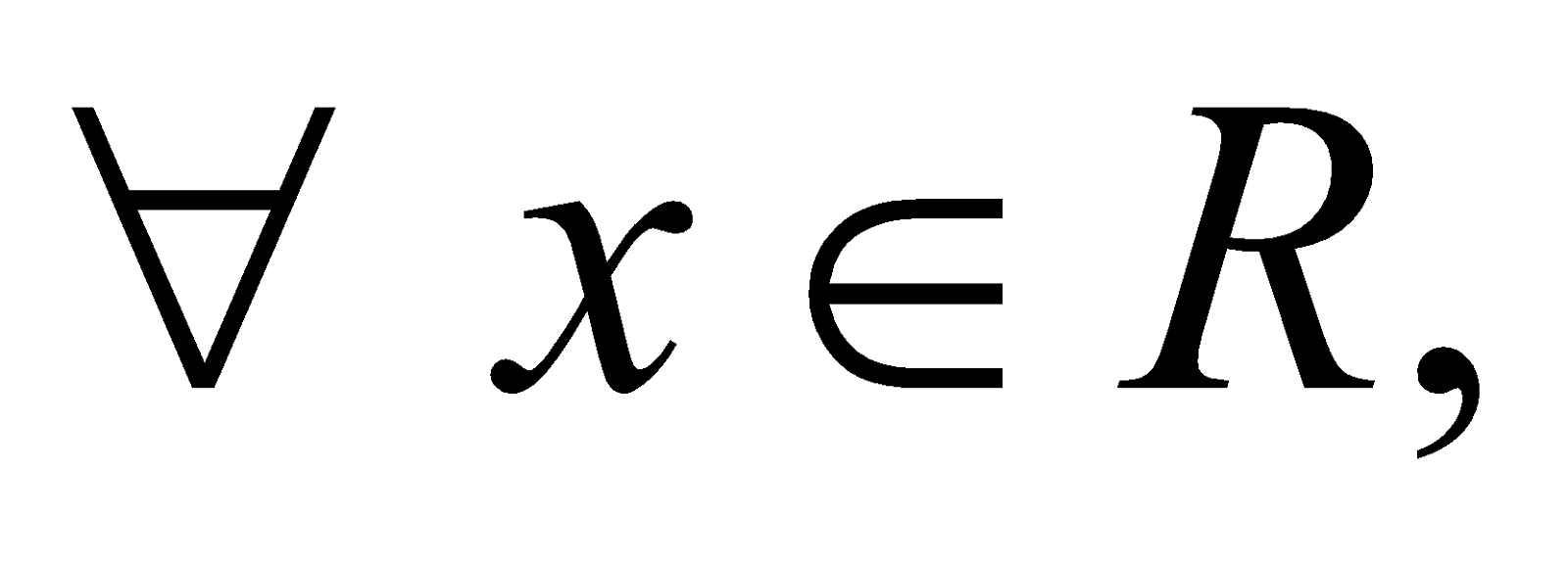
i.e for any x

If D > 0, then find the roots of 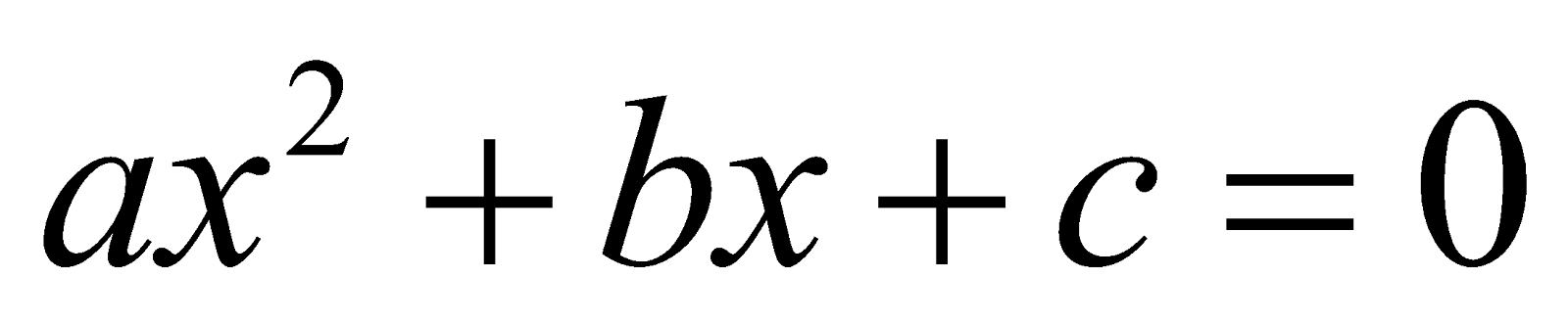, say and. We draw an upward parabola showing the sign scheme as drawn in the figure.

No need to show y-axis. The sign-scheme illustrates that

if

and if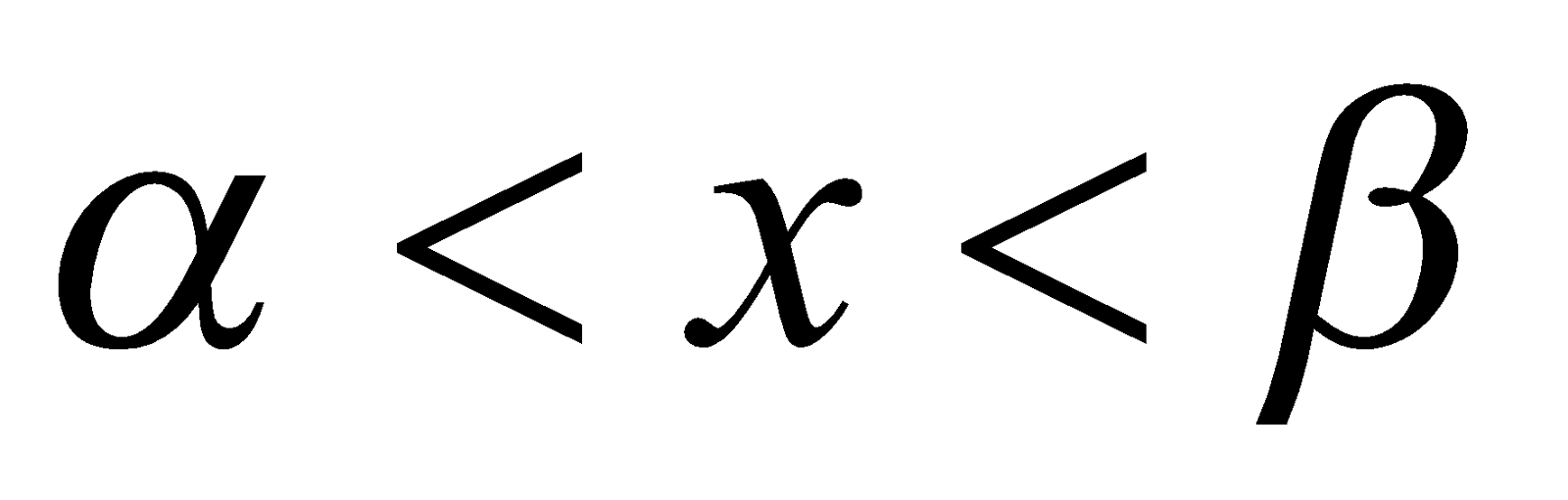

For example :

1. We solve the inequality .

Here D = 1 > 0

Now

We draw the upward parabola with sign - scheme as  shown in the figure.

Since, we have to solve , we consider the interval, with negative sign, which represents,

Hence, the solution to the given inequality is

2. We solve the inequality Here D = –23 < 0

Since, D < 0  

for any x

solution of is (i.e., no solution)

3. We solve the inequality , Here D = –11 < 0 Since, D< 0 . Hence solution set of the inequality is
4. We solve the inequality . Here D = 5 > 0 we first convert the coefficient of x2 positive by multiplying it by –1.

Thus

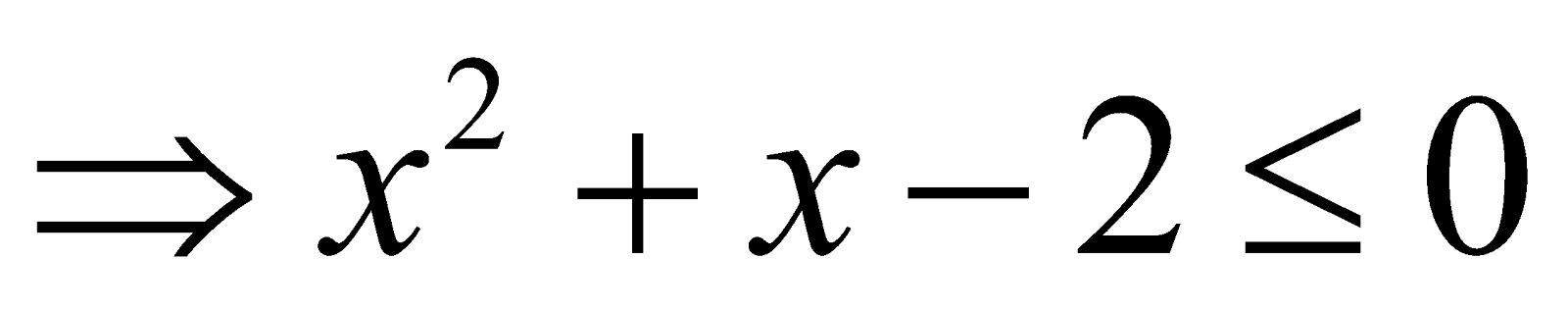
From the adjacent graph and sign-scheme.

5. We solve the inequality .

we have

⇒ –3 < x  < 3 or x ∈ (–3, 3)

PROBLEM RELATED TO EXTREME VALUES OF QUADRATIC EXPRESSIONS

From the analysis of quadratic functions, we have

1. If a > 0, then the minimum value of is and is attained when

So,

2. If a < 0, then the maximum value of f(x) = ax2 + bx + c is and is attained when

So,

For example :

1. If then we find the maximum value of (2 + 3x) (1 – x) the expression is f(x) = (2 + 3x)(1 – x) = 2 + x – 3x2. Here . So the maximum value of  , which occurs at
2. If Then the minimum value of is (Here a > 0)

Now

∴  Minimum value of is 4 and it occurs at

PROBLEMS RELATED TO RANGE OF VALUES OF QUADRATIC RATIONALS

The range of values of quadratic rational can be evaluated with the help of previous articles. It is illustrated in the following example :

Example :

We find the range of values of ,

Let . We express, it as a quadratic in x.

Thus

, lies in the interval

PROBLEMS RELATED TO LOCATING THE ROOTS OF QUADRATIC  EQUATION UNDER GIVEN CONDITIONS

1. Both the roots of equation are greater than a given number m, if , and
2. Both the roots of equation are smaller than a given number M, if, and
3. A given number k lies between the roots of if
4. Exactly one root of lies between the given numbers p and q if . But f(p) and f(q) are not simultaneously zero.
5. Both the roots of lie between two given numbers m and M, if , , and (assuming  m < M)

For example :

Consider the quadratic equation . We will find the values of parameter 'a' under various conditions :

1. If both the roots of given equation are greater than unity, then , and

and

and a < 0

and a < 0

The common values of a among above three solutions are

Hence, both the roots of equation are greater than 1, if

2. If both the roots of given equation are smaller than unity, then and

 and a > 0

The common values of a are

Hence, both the roots of given equation are smaller than 1, if

3. If one root of given equation is greater than unity and other is smaller than unity, then

  [1 lies between the roots of the equation]

Hence, 1 lies between the roots of the equation if

4. If  exactly one root of given equation lies in the interval
   (1,  3), then

Hence, exactly one root of the equation lies between
1 and 3, if

5. If both the roots of given equation lie in the interval then  

and

 and

The common values of a among above four solutions are

Hence, both the roots of equation lie between 1 and 3 if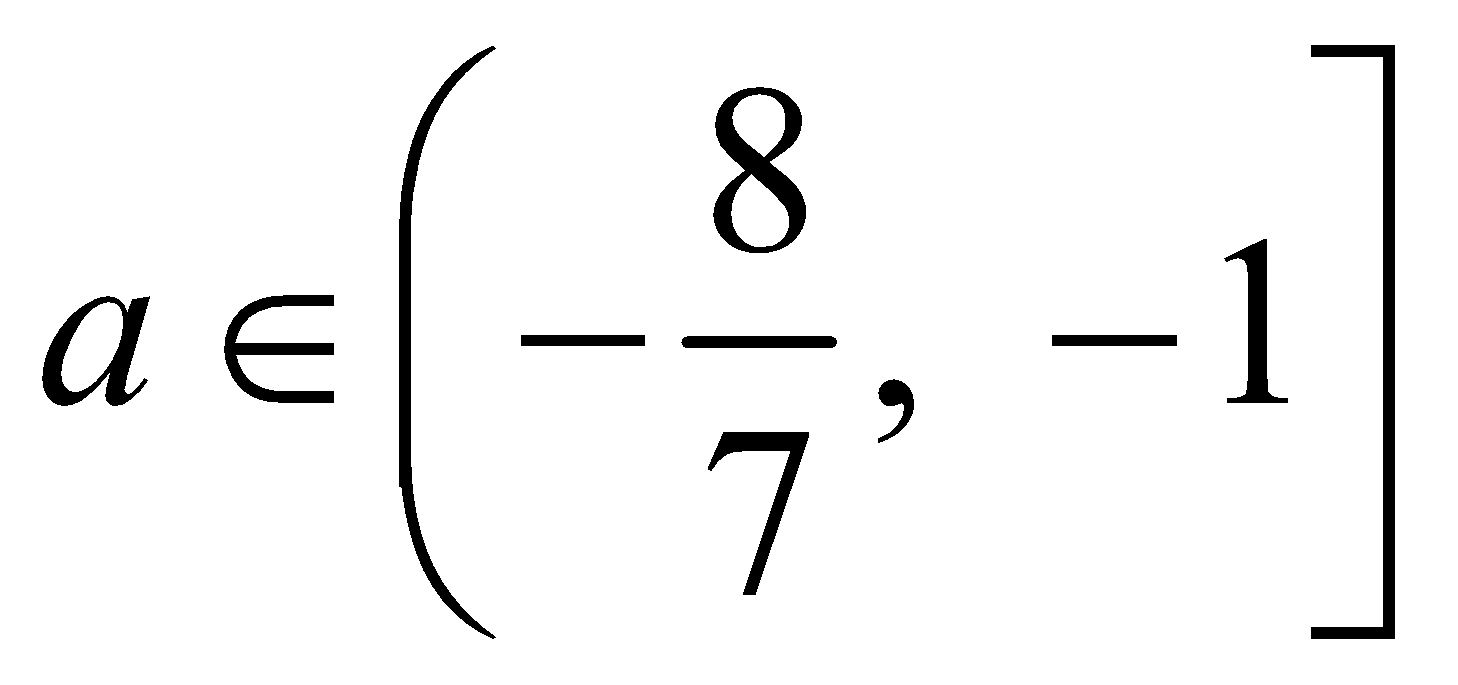

6. If one root is greater than 3 and other root is smaller than 1, then and [1 and 3 lie between the roots] and 7a + 8 < 0

and   

The common values of among above two solutions are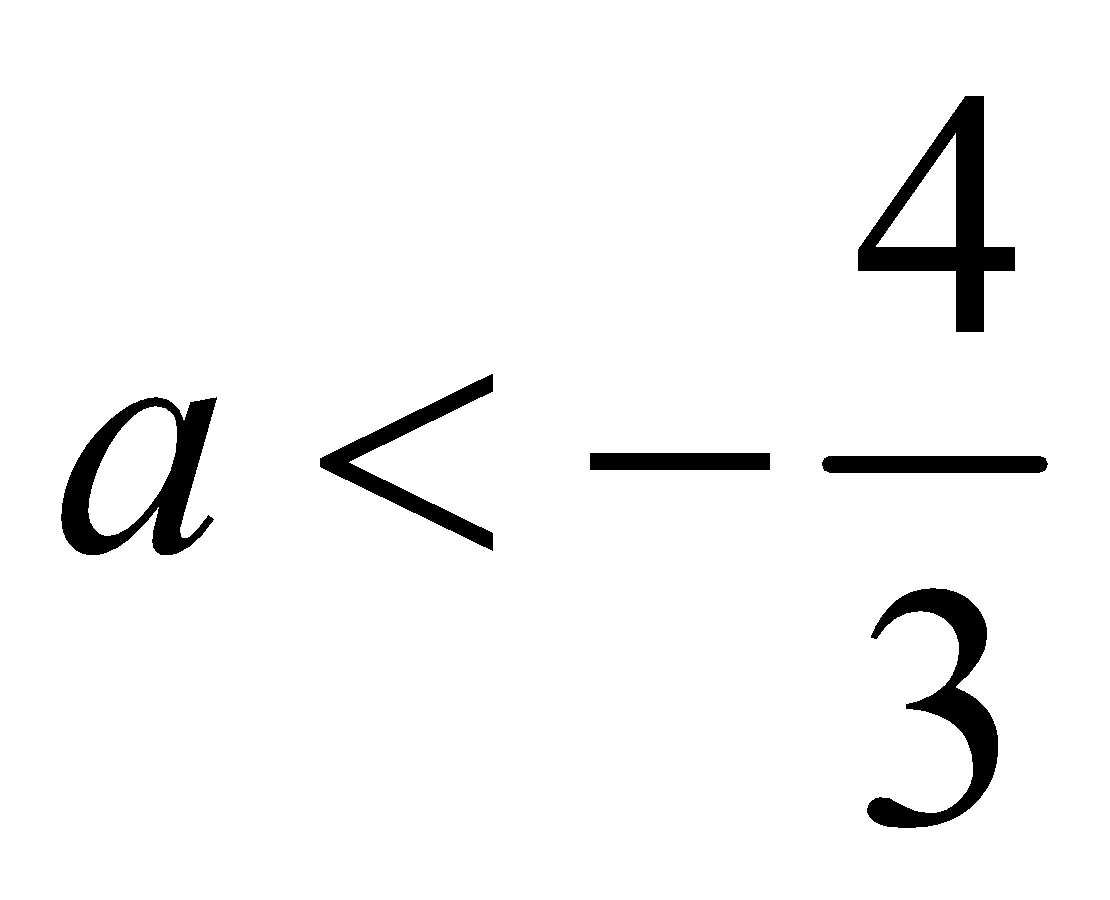

Hence, one root is greater than 3 and other root is smaller than 1 if

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT