DIFFERENTIATION AND APPLICATION OF DERIVATIVES
DIFFERENTIATION OF A FUNCTION
Let f (x) is a function differentiable in an interval [a, b]. That is at every point of the interval, the derivative of the function exists finitely and is unique. Hence we may define a new function  such that
such that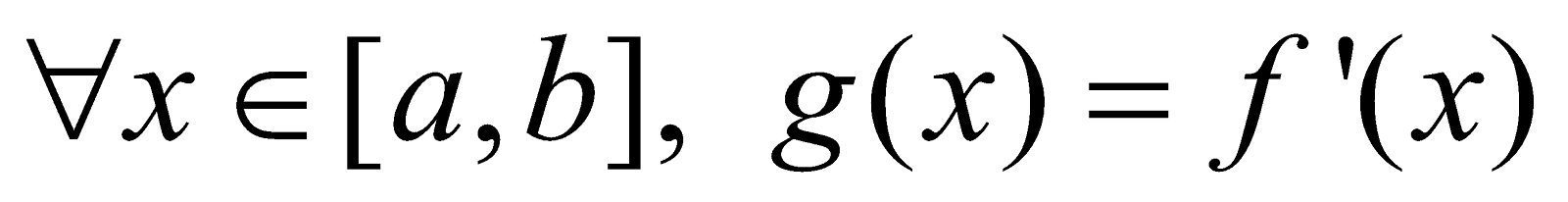
This new function is said to be differentiation or (differential coefficient) of the function f (x) with respect to x and symbolically denoted by
 or f'(x)
or f'(x)
DIFFERENTIATION FROM FIRST PRINCIPLE (AB-INITIO METHOD)
Let f (x) is a function finitely differentiable at every point on the real number line. Then its derivative is given by
SOME STANDARD DIFFERENTIATIONS
where k is constant
FUNDAMENTAL RULES FOR DIFFERENTIATION
if and only if f (x) = C, where C is a constant.
when c is a constant.
(PRODUCT RULE)
In short if u and v are two differentiable functions of x, then
Generalization : If u1, u2, u3,......un be differentiable functions of x, then
(QUOTIENT RULE)
- If
Example :
DIFFERENTIATION OF COMPOSITE FUNCTIONS (CHAIN RULE)
If f and g are differentiable functions in their domain. then fog is also differentiable and (fog)’(x) = f’(g(x)) g’(x)
More easily if y = f (u) and u = g (x), then 
If y is a function of u, u is a function of v and v is a function of x.
Then 
Similarly we can extend the result further
DIFFERENTIATION OF INVERSE TRIGONOMETRIC FUNCTIONS
In order to find differential coefficients of complicated expressions involving inverse trigonometric functions some substitutions are very helpful, which are listed below :
If the function contains suggested substitution
x = a sinθ or a cos θ
x = a tan θ or a cot θ
x = a sec θ or a cosec θ
x = a cos 2 θ
x = r cos α, b = r sin α
x = α sin2 θ + β cos2 θ
x = a (1– cos θ)
DIFFERENTIATION OF IMPLICIT FUNCTIONS
If f (x, y) = 0. Differentiate with respect to x and collect the terms containing  at one side and find
at one side and find  .
.
For example :
- If
Differentiating both the sides with respect to x
- If
We have, 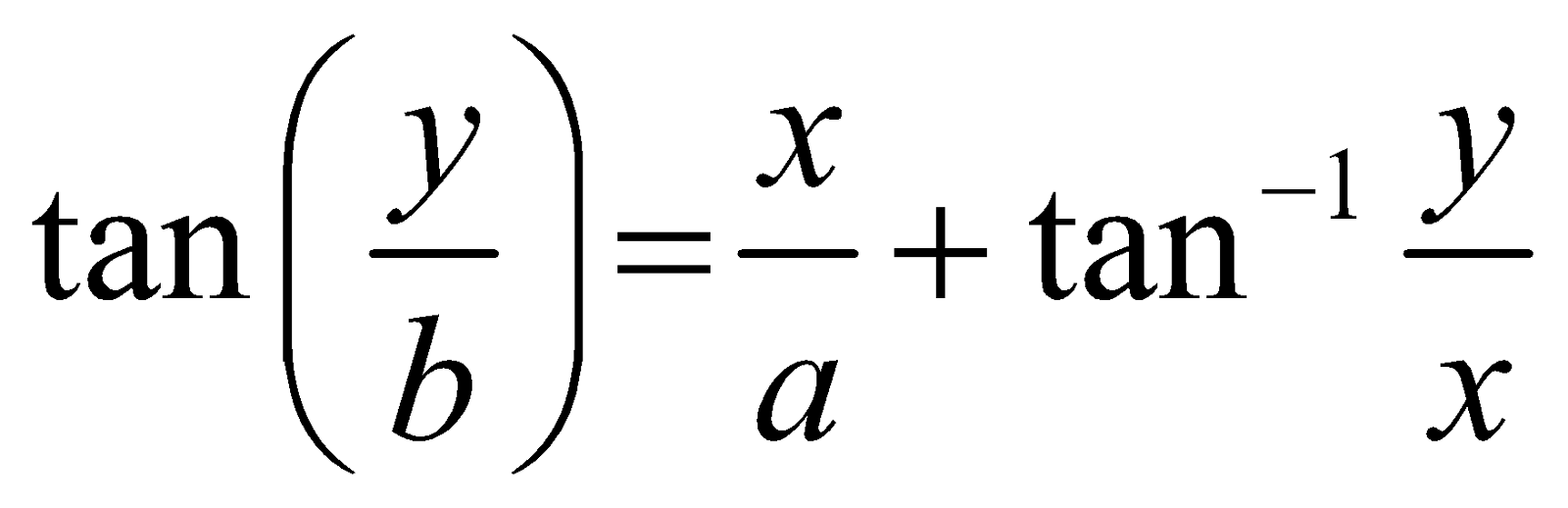
Differentiating both the sides with respect to x, we get
DIFFERENTIATION OF PARAMETRIC FUNCTIONS
If x = f(t), y = g (t), t is parameter then
For example :
- If x = a cos3t, y = b sin3t then
- If x = a sin 2θ (1 + cos2 θ) and y = b cos2 θ (1–cos2θ)
Then find 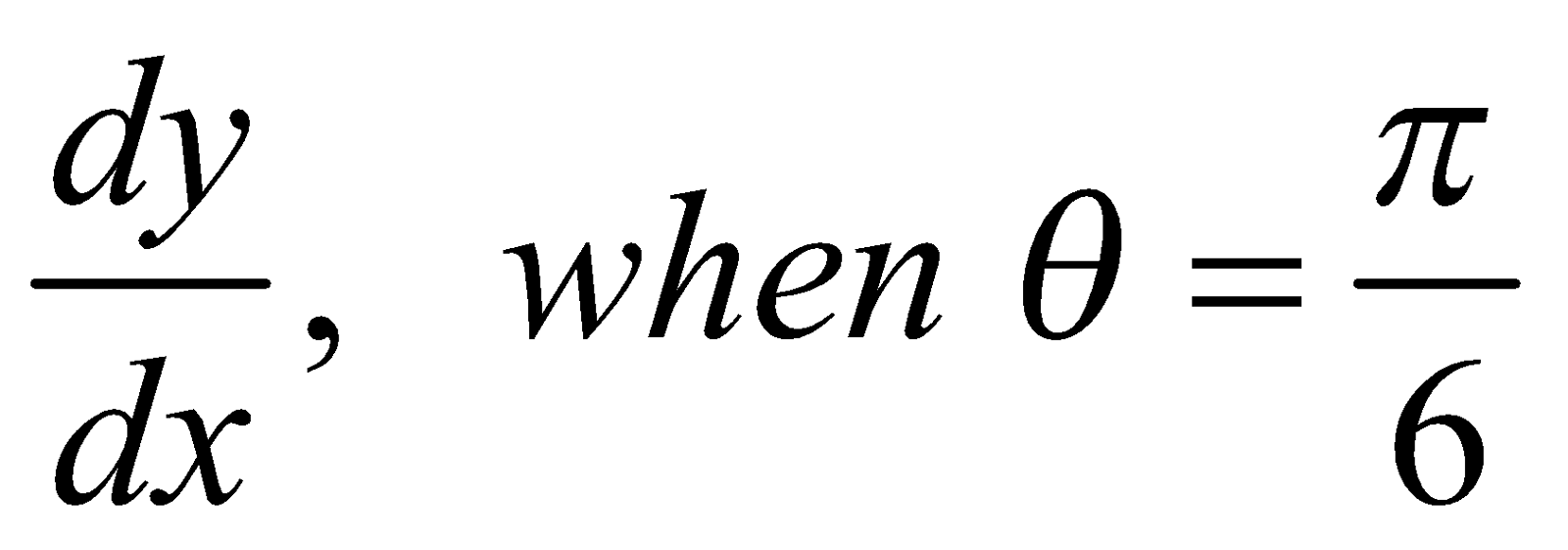
LOGARITHMIC DIFFERENTIATION
- If a function is product and quotient of many simpler functions such as
we first take logarithm and then differentiate.
For example : If 
Taking log of both the sides, we get
Differentiating both the sides, we get
- If a function is in the form of exponent of a function over another function such as [f(x)]g(x), we first take logarithm and then differentiate.
Example 1 : If 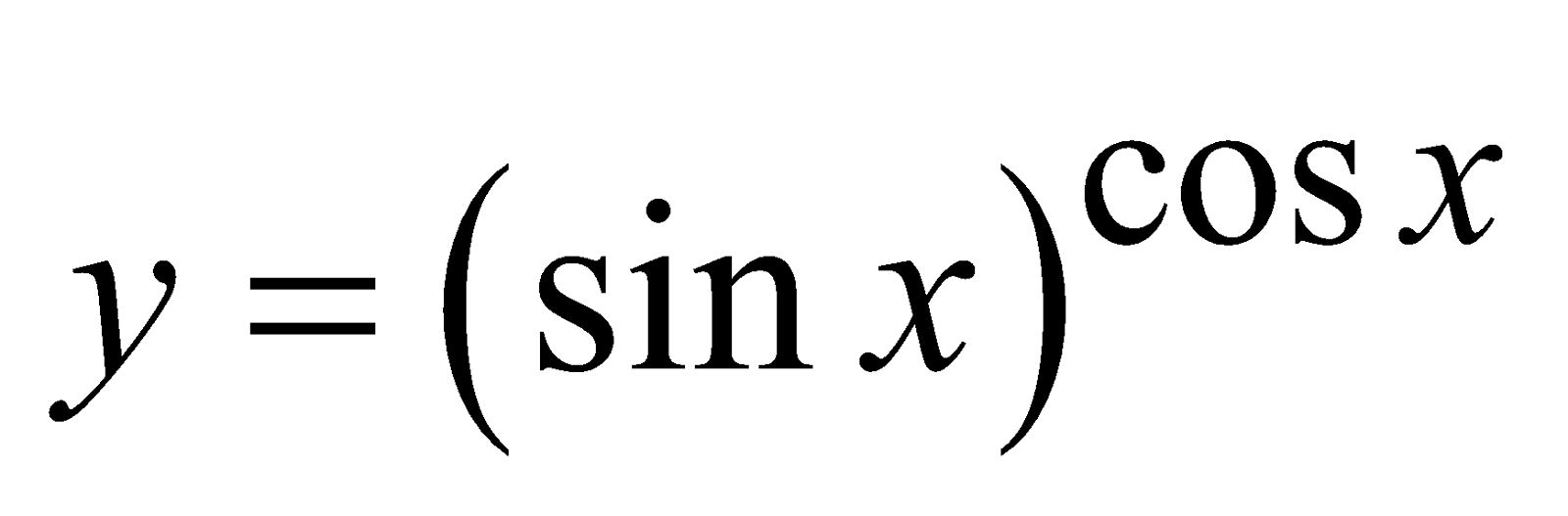
Take log of both the sides, then
log y = cos x log (sin x)
Differentiate both the sides with respect to x, then
⇒ 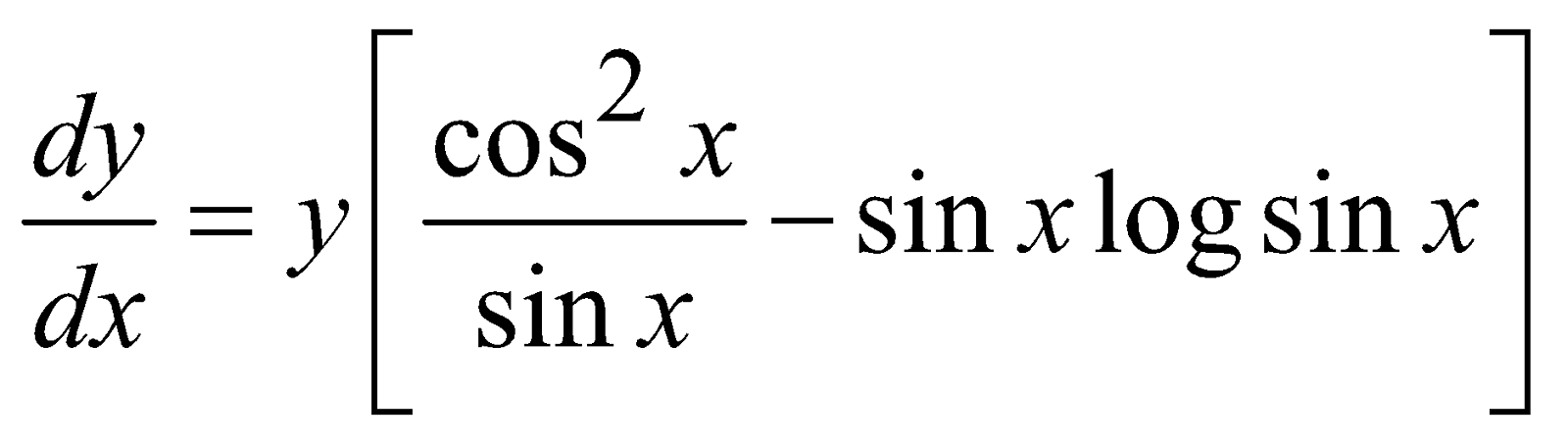
∴ 
Example 2 : If  .
.
Taking log of both the sides, we get
Taking log again, we get
Differentiating both the sides, we get
DIFFERENTIATION OF A FUNCTION WITH RESPECT TO ANOTHER FUNCTION
Let y = f (x) and z = g (x). Then the differentiation of y with respect to z is
Example 1 : Differentiate x2ex with respect to sin x log (x + 1)
Let y = x2 ex ⇒ 
Let z = sin x log (x + 1) ⇒
Derivative of y with respect to z, i.e.
= 
Example 2 : Differentiate with respect to
with respect to 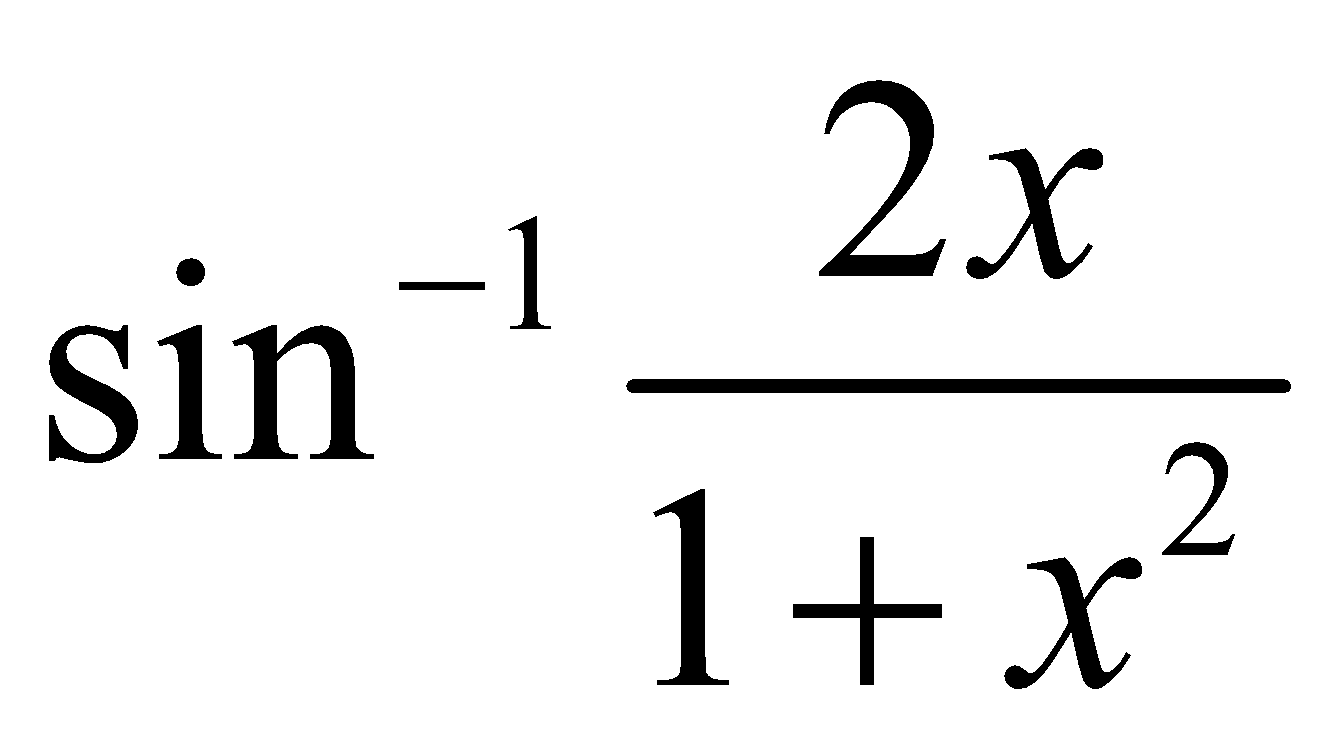
Let, 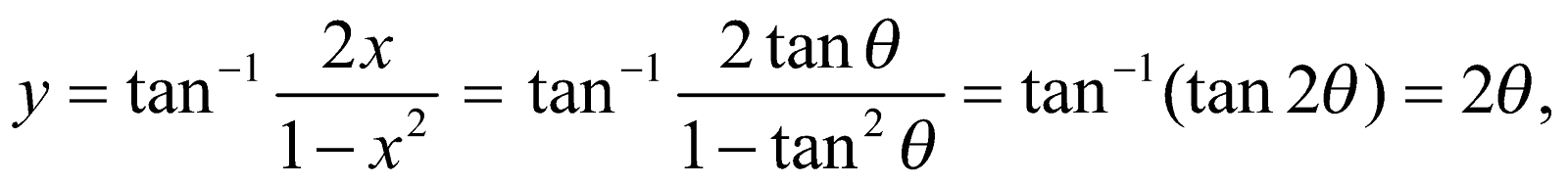
Where x = tan  .
. 
Again let, 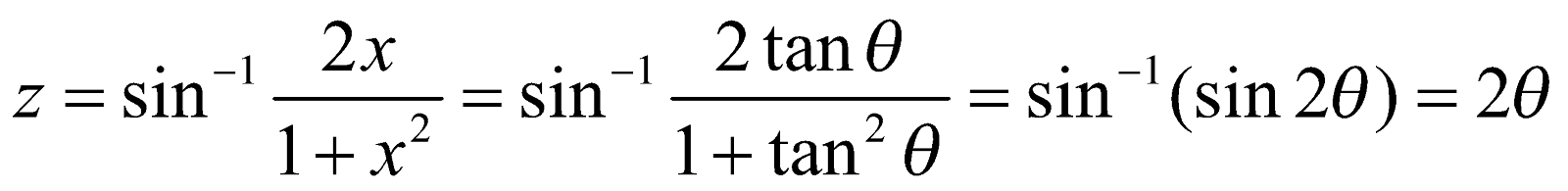
where x = tan θ
SUCCESSIVE DIFFERENTIATIONS
If the function y = f (x) be differentiated with respect to x, the result  so obtained is a function of x (or may be a constant).
so obtained is a function of x (or may be a constant).
Hence can again be differentiated with respect of x.
can again be differentiated with respect of x.
The differential coefficient of 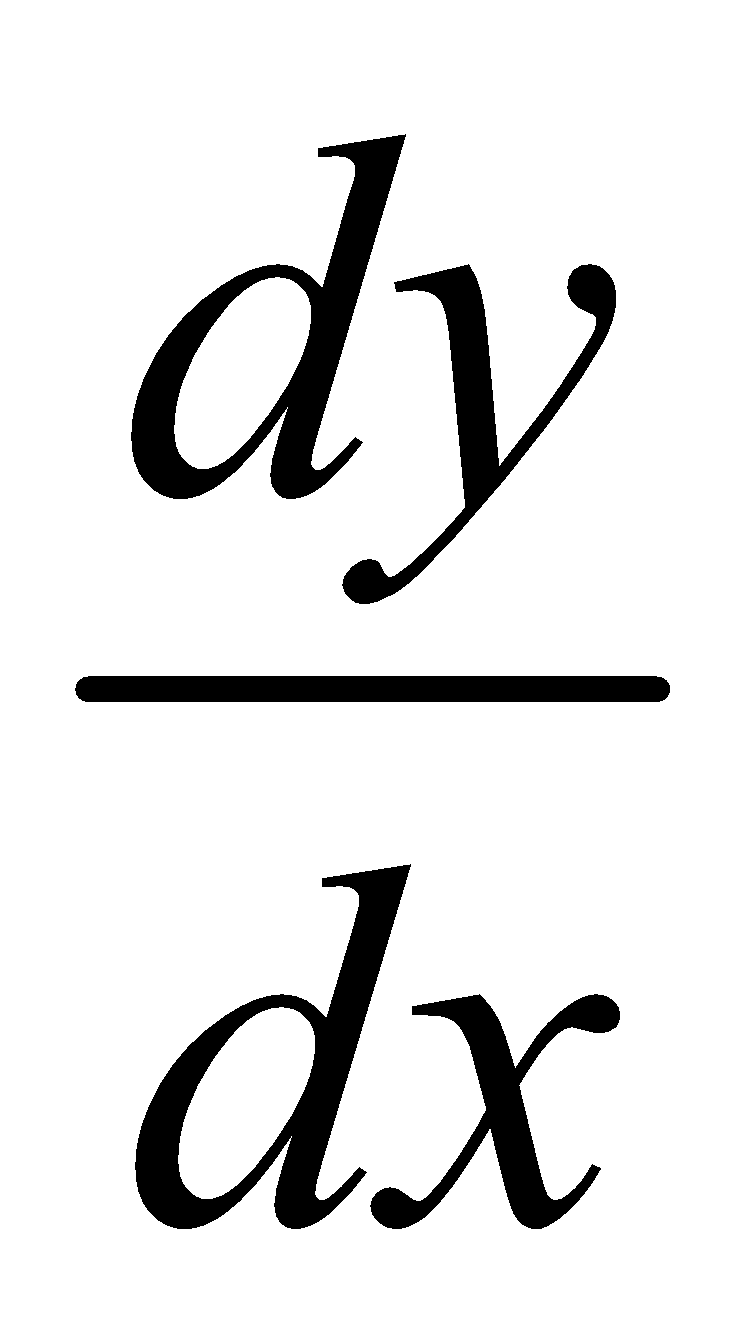 with respect to x is written as
with respect to x is written as  Again the differential coefficient of
Again the differential coefficient of  with respect to x is denoted by
with respect to x is denoted by 
For example :
- If x = a sec2θ, y = a tan3θ. Then
Further, 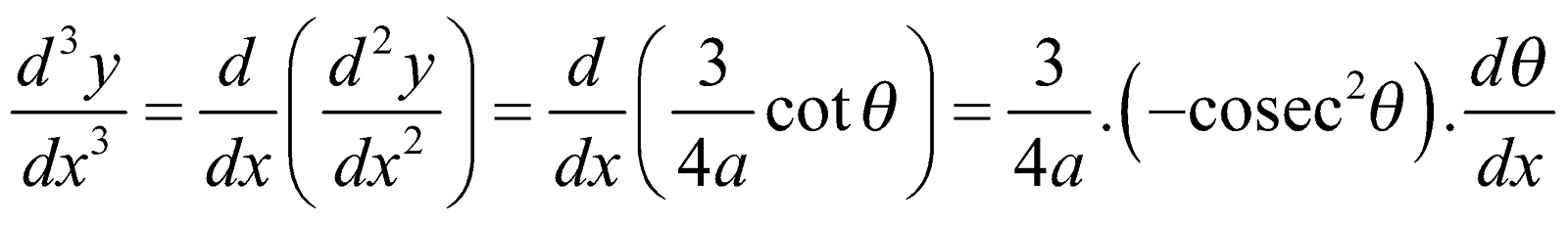
APPLICATION OF DERIVATIVES
TANGENTS AND NORMALS
To Find Cartesian Equation of Tangents and Normals to a Curve
Let y = f (x) be the equation of a continuous curve andP (x, y) be any point on it. Then 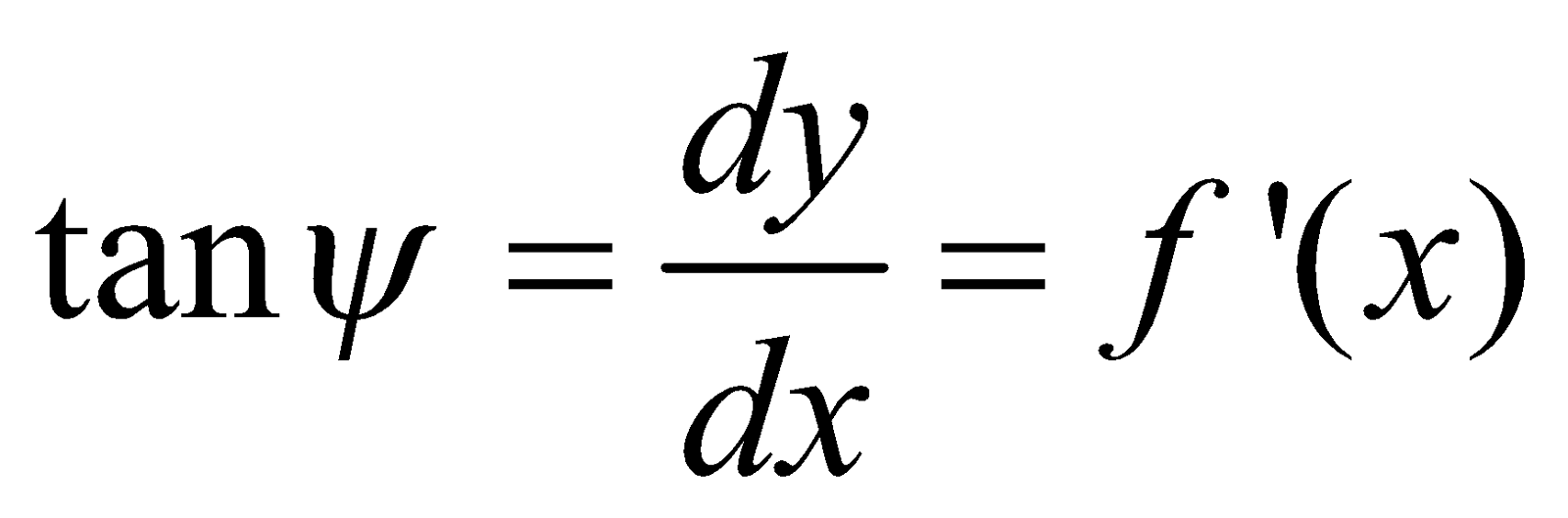 represents the slope of tangent to the curve y = f (x) atP (x, y).
represents the slope of tangent to the curve y = f (x) atP (x, y).
Therefore, the equation of the tangent to the curve at P is
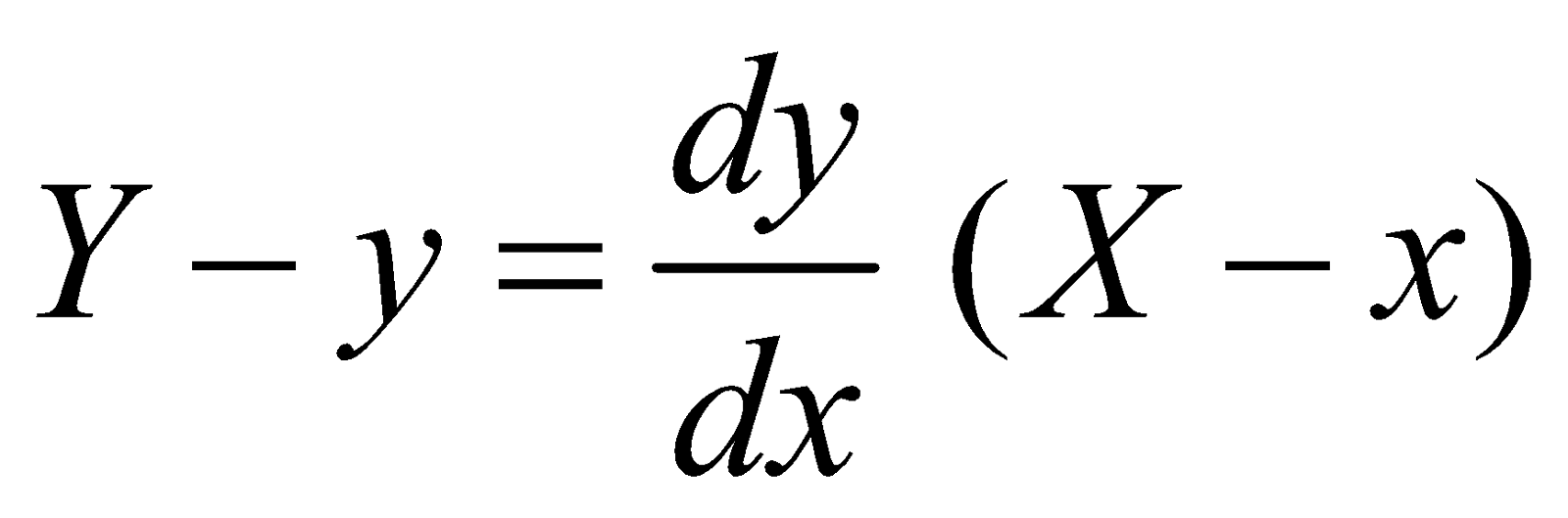
where (X, Y) is an arbitrary point on the tangent.
The slope of the normal at the point (x, y) is 
Therefore, the equation of normal at (x, y) to the curve is 
IMPORTANT NOTES
- If
the tangent makes an acute angle with the x-axis
- If
the tangent makes an obtuse angle with the x-axis
- If
the tangent to the curve is parallel to x-axis
- If the tangent to the curve is perpendicular to x-axis, then
- If the tangent is equally inclined to the axes, then
ANGLE OF INTERSECTION OF TWO CURVES
Let y = f1(x) and y = f2 (x) be the two curves, meeting at some point P (x1, y1), then the angle between the two curves at P (x1, y1) = the angle between the tangents to the curves at P(x1, y1).
∴ The angle of intersection of two curves θ is given by
Such curves are called ORTHOGONAL CURVES.
Then the curves are tangential at (x1, y1).
MONOTONICITY OF FUNCTIONS
Let f (x) be any continuous function, defined in the interval [a, b] and its derivative f’(x) be finite for a < x < b. Then
- The function f (x) is said to be monotonically increasing (or non-decreasing) in the interval [a, b], if
The function f (x) is monotonically increasing in [a, b] if f’(x) ≥ 0 for all x∈[a, b]
- The function f (x) is said to be monotonically decreasing (or non-increasing) in the interval [a, b], if
The function f (x) is monotonically decreasing in [a, b] if f’(x) ≤ 0 for all x∈[a, b]
IMPORTANT NOTES
- The function f (x) is said to be strictly increasing in the interval [a, b],
if 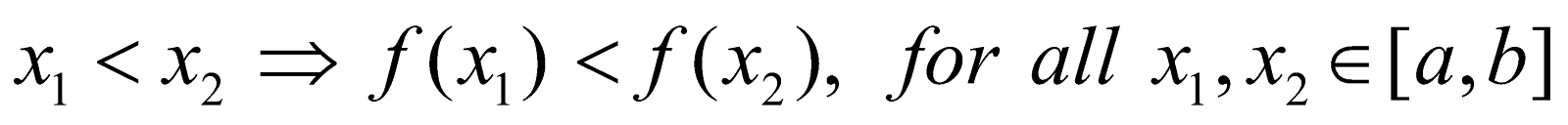
The condition for the function f (x) to be strictly increasing in [a, b] is that f’(x) > 0 for all x∈[a, b], except at some discrete points at which the derivative may vanish.
- The function f(x) is said to be strictly decreasing in the interval [a, b],
if  .
.
The condition for the function f(x) to be strictly decreasing in [a, b] is that f’(x) < 0 for all x∈ [a, b], except at some discrete points at which the derivative may vanish.
- The function f(x) is said to be monotonic in the interval [a, b] if either f(x) is monotonic increasing or monotonic decreasing in [a, b] but not both.
Example :
- f (x) is increasing if
∴ f (x) increases in (– ∞, –2) ∪ (3, + ∞)
- f (x) is decreasing if f’(x) < 0 ⇒ (x – 3) (x + 2) < 0 ⇒ –2 < x < 3
∴ f (x) decreases in (–2, 3).
Example :

Since 
∴ f (x) increases in (0, + ∞), f (x) decreases in (–1, 0).
MAXIMA AND MINIMA OF FUNCTIONS
MAXIMUM AND MINIMUM VALUES (EXTREME VALUES)
- A function y = f (x) is said to have a local maximum at a point x = a if f (x) ≤ f (a) for all x∈ (a – h, a + h) where h is somewhat small but positive quantity.
The point x = a is called a point of maximum of the function f (x)
- The function y = f (x) is said to have a local minimum at a point x = a, if f(x)
f (a) for all x∈ (a – h, a + h) where h is somewhat small but positive quantity.
The point x = a is called a point of minimum of the function f (x).
NECESSARY CONDITION FOR EXISTENCE OF EXTREME VALUES
If f (x) be a differentiable function. Then f’(x) vanishes at every local maximum and at every local minimum.
IMPORTANT POINTS
- The converse of above is not true, that is, every point at which f’(x) vanishes need not be a local maximum or minimum. For example, if f (x) = x3, then f’(0) = 0, but at x = 0. The function has neither minimum nor maximum. In general these points are point of inflection.
- A function may attain an extreme value at a point without being derivable there at, for example f(x) = |x| has a minima at x = 0 but f’(0) does not exist.
- A function f(x) can have several local maximum and local minimum values in an interval. Thus, the maximum and minimum values of f(x) defined above are not necessarily the greatest and the least values of f(x) in a given interval.
- A minimum value at some point may even be greater than a maximum value at some other point.
METHODS TO FIND LOCAL EXTREMUM
- FIRST DERIVATIVE TEST
Let f (x) be a differentiable function on an interval I and a ∈ I. Then
- a is a point of local maximum of f (x) if
- f’ (a) = 0
- f’(x) > 0 if x ∈ (a – h, a) and f’(x) < 0 if x ∈ (a, a + h), where h is a small but positive quantity.
- a is a point of local minimum of f(x) if
- f’(a) = 0
- f’ (x) < 0 if x ∈ (a – h, a) and f’(x) > 0 if x ∈ (a, a + h), where h is a small but positive quantity.
- If f’(a) = 0 but f’(x) does not changes sign in (a – h, a + h), for any positive quantity h, then x = a is neither a point of minimum nor a point of maximum.
Example :
If f (x) = x5 – 5x4 + 5x3 – 1,
then
f’(x) = 0 gives x = 0, 1, 3.
To check for the sign scheme of f’(x) we use the method of intervals. Plotting f’(x) = 5x2 (x – 1) (x – 3) on real number line.
From the figure we see that f’(x) remains positive to the left as well as right of x = 0. Therefore f (x) has neither maximum nor minimum at x = 0
Further, at x = 1, f’(x) is positive to the left of x = 1 and negative to the right of x = 1. Hence at x = 1, f (x) has maxima.
Now, at x = 3, f’(x) changes sign from negative to positive,
thus, f(x) has a minima at x = 3.
- SECOND DERIVATIVE TEST
Let f(x) be a twice differentiable function on an interval I. Let a∈I is such that f’’(x) is continuous at x = a. Then
- x = a is a point of local maximum if f’(a) = 0 and f’’(a) < 0
- x = a is a point of local minimum if f’(a) = 0 and f’’(a) > 0
- If f’(a) = f’’(a) =0, but f’’’(a) 0, if exists then x = a is neither a point of local maximum nor a point of local minimum.
Example :
If f(x) = xe–x, then
f’(x) = e–x – xe–x = (1 – x)e–x
f’’(x) = – e–x – (1 – x)e–x = – (2 – x) e–x
for maxima or minima, f’(x) = 0 ⇒(1 – x) e–x = 0 ⇒ x = 1
Now, at x = 1. f’’ (1) = – e–1 = 
∴ f(x) has a local maximum at x = 1.
The maximum value = f (1) = 1e–1 =
MAXIMUM AND MINIMUM VALUES IN A CLOSED INTERVAL
Let the function f(x) is defined in the closed interval [a, b]
- The value f(α) is said to be the greatest value of f(x) in [a, b] if f(x) ≤ f(α) for all x ∈ [a,b], for some. The value f (α) is also known as GLOBAL MAXIMUM OR ABSOLUTE MAXIMUM of f(x) in [a, b].
- The value f (β) is said to be the least value of f(x) in [a, b] if f(x) ≥ f(β) for all x ∈ [a, b], for some. The value of f(β) is also known as GLOBAL MINIMA OR ABSOLUTE MINIMA of f(x) in [a, b].
- The point on the curve y = f(x) at which either f’(x) = 0 or f’(x) does not exist, are known as the CRITICAL POINTS.
- If a function f(x) is continuous in [a, b], then it attains its greatest and least values either at critical points or at the end points of the interval.
Thus, suppose that f (x) is continuous in [a, b] such that f(x) = 0 at x = c1, c2,.........in [a,b].
f’(x) does not exist at x = d1, d2, ....... in [a, b]. Then,
Absolute maxima = Max {f(a), f(c1) f(c2) ........, f(d1), f(d2).........f(b)}
Absolute minima = Min {f (a), f(c1), f(c2), ........f(d1) f(d2), ........f(b)}
Example :
Consider the function f(x) = x50 – x20 on the interval [0, 1]
We have f’ (x) = 50x49 – 20x19
f’(x) = 0 . Now, f (0) = 0, f (1) = 0 and
. Now, f (0) = 0, f (1) = 0 and
∴ Absolute maximum 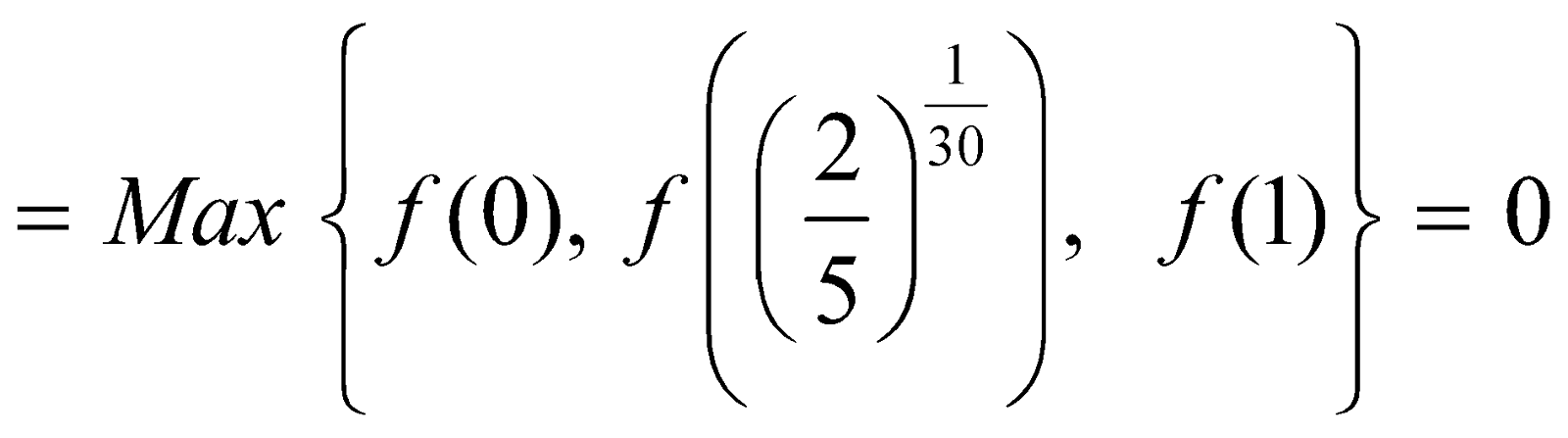
Absolute minimum 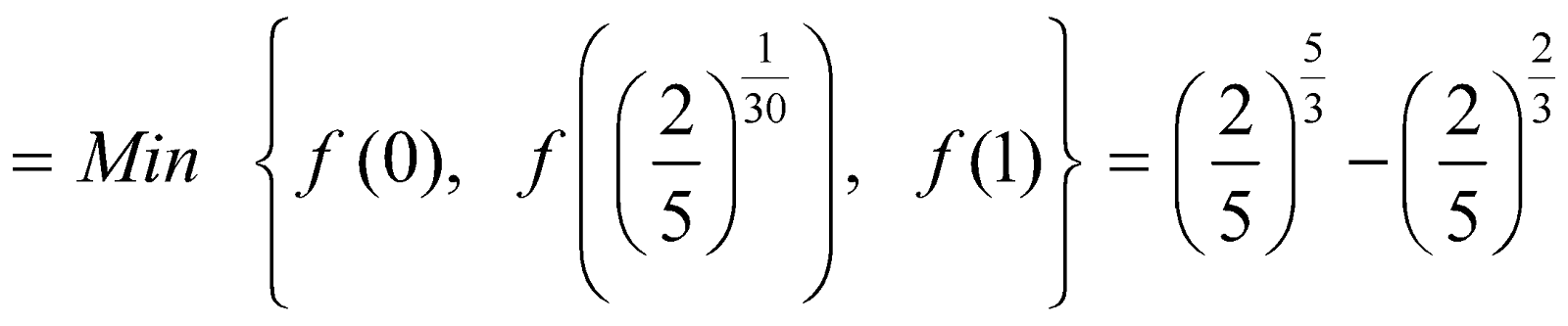
[Note that there in no need to apply first derivative test or second derivative test for maxima or minima].
- To find range of a continuous function
Let f(x) be a continuous function on [a, b] such that its least value in [a, b] is m and the greatest value in [a, b] is M. Then range of value of f(x) for x ∈ [a, b] is [m, M]
- To check for the injectivity of a function
A strictly monotonic function is always one-one (injective). Hence, a function f(x) is one-one in the interval [a, b] if f '(x) > 0 ∀ x ∈ [a, b] or f '(x) < 0 ∀ x ∈ [a, b]
f '(x) can vanish at some discrete points.
f '(x) can vanish at some discrete points.
Example : f (x) = x3, then f’(x) = 3x2 clearly f '(x) > 0 for all x ∈ R except that at x = 0, where f’(x) = 0
∴ f(x) is one-one for all x ∈ R.
MEAN VALUE THEOREMS
ROLLE’S MEAN VALUE THEOREM
Let f be a real function defined in the closed interval [a, b] such that :
- f (a) = f(b)
- f is continuous in the closed interval [a, b]
- f (x) is differentiable in the open interval (a, b)
Then there is some point c in the open interval (a, b) such that f’(c) = 0.
Geometrical Meaning of Rolle’s Theorem
Under The assumptions of Rolle’s theorem, the graph of f starts at (a, 0) and ends at (b, 0) as shown in figures.
The conclusion is that there is a point c between a and b. such that the tangent to the graph at (c, f(c)) is parallel to the x-axis.
Note :
- There can be more than one-such points
- If f(x) be a polynomial function such that α and β are its zeros. That is f (α) = 0 and f (β) = 0
Since a polynomial function is continuous and differentiable everywhere on the real number line, hence the conditions of Rolle’s theorem are satisfied. Then there exists γ, such that
f’(γ) = 0, α < γ < β
Alternatively : Between two roots of a polynomial equation f(x) = 0, there exists a root of the equation f’(x) = 0
LAGRANGE’S MEAN VALUE THEOREM
Let f be a real function, continuous on the closed interval [a, b] and differentiable in the open interval (a, b). Then there is a point c in the open interval (a, b) such that
Remarks :
In the particular case where f(a) = f(b).
The expression  becomes zero. Thus when
becomes zero. Thus when
f(a) = f(b), f’(c) = 0 for some c in (a, b).
f(a) = f(b), f’(c) = 0 for some c in (a, b).
Thus Rolle’s theorem becomes a particular case of the mean value theorem.
Note :
- There can be more than one such c in an interval.
- Geometrically, we may state the lagrange’s mean value theorem as “Given any chord of the curve y = f(x), there is a point on the graph where the tangent is parallel to this chord.
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
- Let y = f(x) be a given function. Let Δx denotes a small increment in x, corresponding which, y increases by Δy. Then for small increments, we assume that
[Symbol stands for “approximately equal to”]
Example :
Let us find approximate value of .
.
We know that 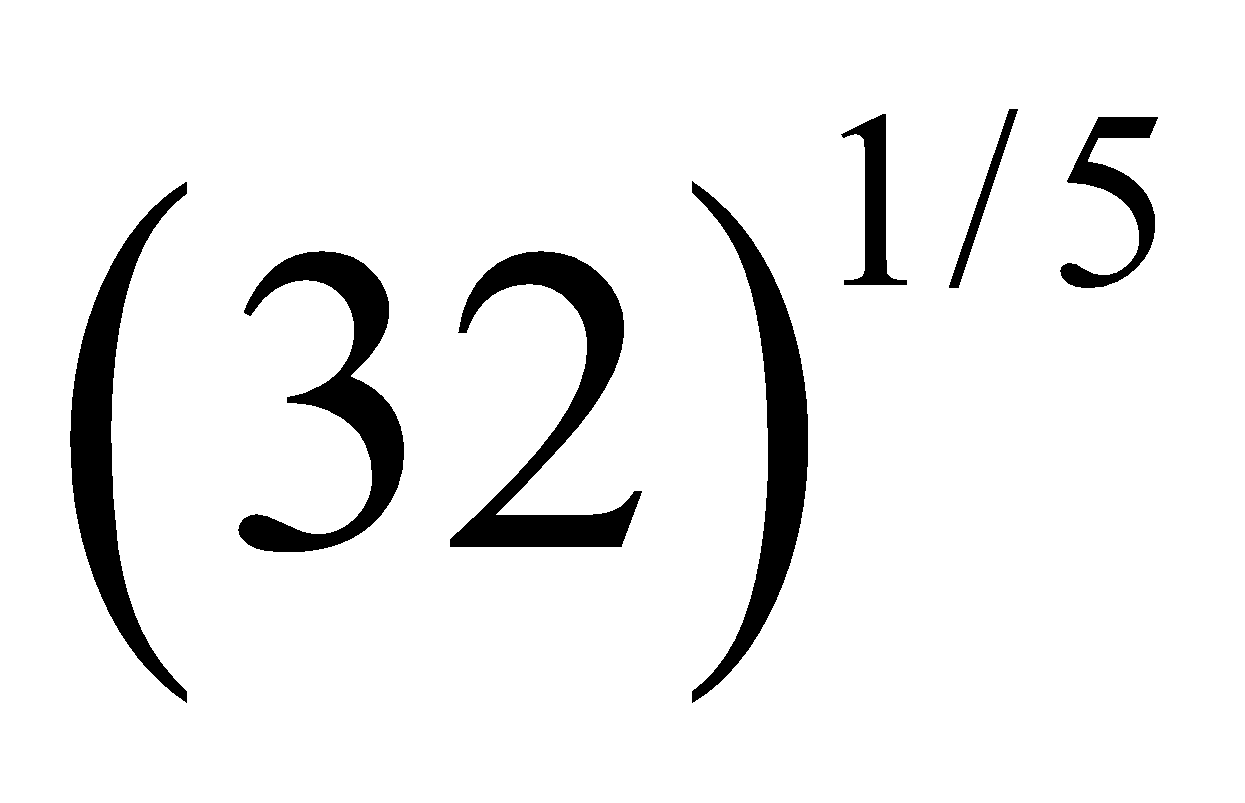 = 2.
= 2.
Let 
Now, 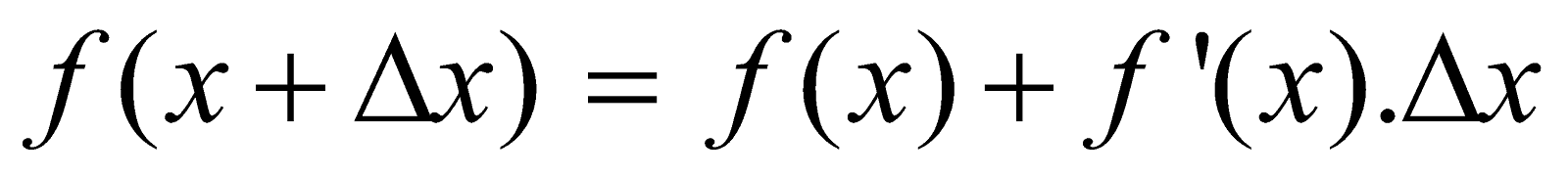
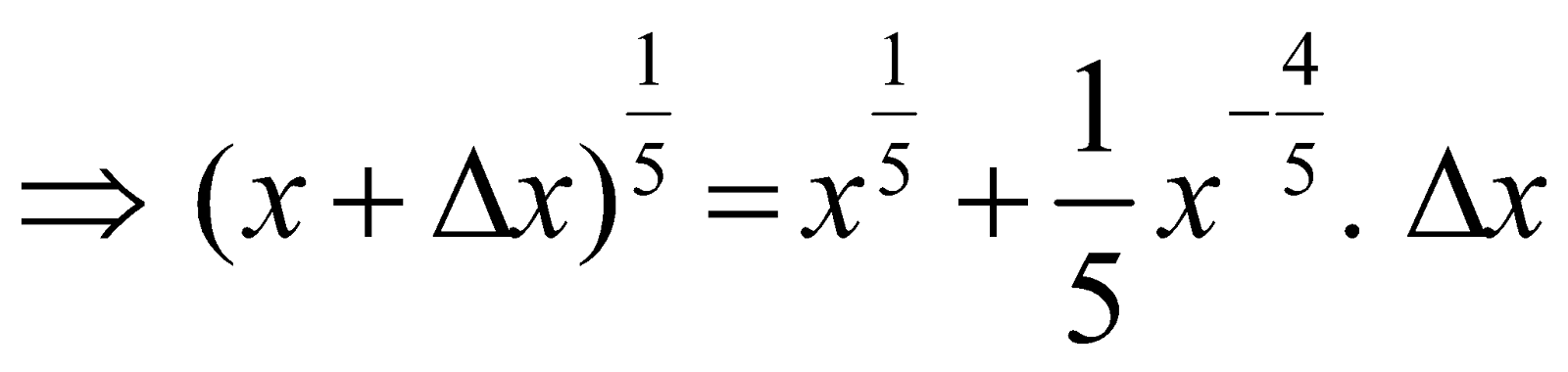
Take x = 32, Δx = 1. Then 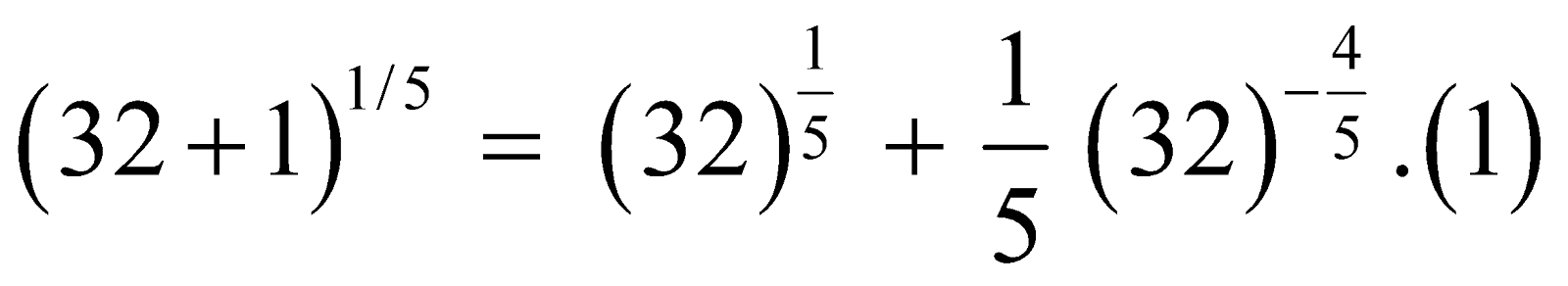
- Let Δx be the error in the measurement of independent variable x, and
Δy is corresponding error in the measurement of dependent variable y.
Then
Δy = absolute error in measurement of y
Example :
The time period T of oscillation of a simple pendulum of length l is given by 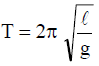 . Suppose an error in measurement of l is found to be 1% Let us calculate the corresponding error is measurement of T. We have
. Suppose an error in measurement of l is found to be 1% Let us calculate the corresponding error is measurement of T. We have
Differentiating we get, 
Given 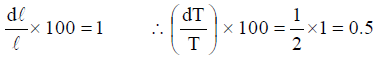
∴ Percentage error in measurement of T = 0.5%
APPLICATION OF dy/dx AS A RATE MEASURER
- Let x = f (t). Then rate of change of x w.r. to t =
- Let x = f(t) and y = g (t) are two variables dependent on t. Then,
rate of change of y w.r. to 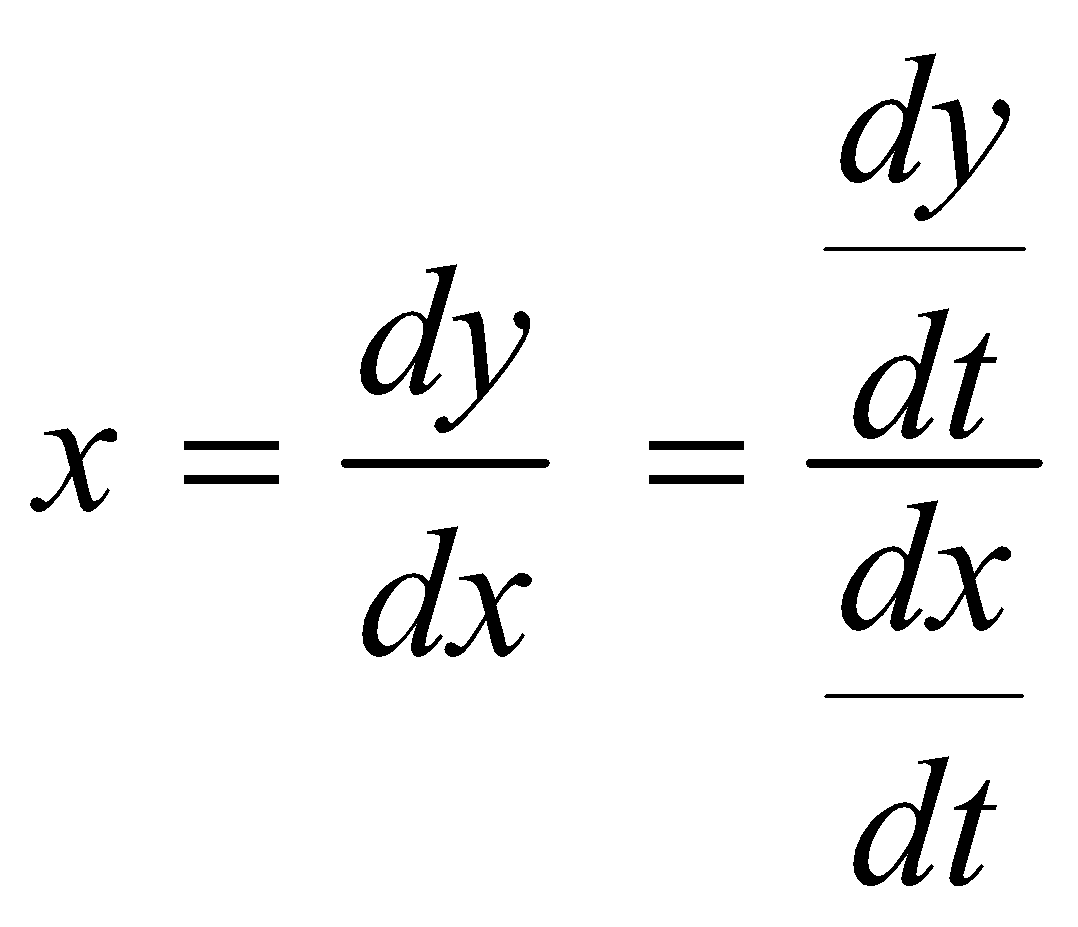
- Let displacement s is a function of time t.
Then, velocity at a time acceleration at a time t,







