Points & Straight Lines | Mathematics Notes for IITJEE Main

POINTS AND STRAIGHT LINES

CARTESIAN COORDINATE SYSTEM

Consider two mutually perpendicular straight lines X'OX and Y'OY in a plane intersecting at O. The point O is called the origin. The horizontal line X'OX is called x-axis and the vertical line Y'OY is called y-axis. Any point P in this plane can be uniquely represented by specifying its distance from the two lines X'OX and Y'OY. For this complete the rectangle OMPN.

The distance x of the point P from the y-axis, i.e. PM = ON = x is called x-coordinate (or abscissa) of the point P. The distance y of the point P from the x-axis, i.e. PN = OM = y is called y-coordinate (or ordinate) of the point P. The ordered pair (x, y) is called the coordinates of the point P.

Distances measured along x-axis right to the origin are taken positive and left to the origin are taken negative. Similarly, distances measured along y-axis above the origin are taken positive and below the origin are taken negative.

The coordinate axes X'OX and Y'OY divide the plane into four parts, called QUADRANTS number I, II, III and IV. Thus

In I Quadrant, x > 0 and y > 0

In II Quadrant, x < 0 and y > 0

In III Quadrant, x < 0 and y < 0

In IV Quadrant, x > 0 and y < 0.

Further, if the abscissa of a point is zero, it will lie on the y-axis and if the ordinate is zero the point will lie on the x-axis. The coordinates of origin O are clearly (0, 0).

DISTANCE FORMULA

Let P and Q be two points with coordinates (x1, y1) and (x2, y2) respectively. The distance between them is  

IMPORTANT RESULTS

1. The distance of a point P (x, y) from the origin O is
2. If the line PQ is parallel to the y-axis, then x1 = x2, i.e. the abscissae of the points are equal and then
3. If the line PQ is parallel to the x-axis, then y1 = y2, i.e. the ordinates of the points are equal and then

SECTION FORMULA

Let P (x, y) be a point on the line joining two points A (x1, y1) and B (x2, y2) dividing it, in the ratio m : n, i.e. .

If P lies within the points A and B, then P is said to divide AB internally.

We have and

If P lies without the points A and B, i.e. on the line AB extended then P is said to divide AB externally.

We have and

IMPORTANT RESULTS

1. The coordinates of the mid-points of the line segment joining A (x1, y1) and B (x2, y2) are given by .
2. The coordinates of the points of trisection P and Q of the line segment joining A (x1, y2) and B(x2, y2) are given by and .

[The points of trisection are the points dividing AB in three equal parts, i.e. one divides AB internally in ratio 1 : 2 and the other divides AB internally in ratio 2 : 1].

3. Any point P on the line joining two points A (x1, y1) and B (x2, y2) may be taken as , λ is parameter. λ ≠ –1

RESULTS OF TRIANGLE

Let ABC be a triangle such that the coordinates of its vertices are A (x1, y1), B (x2, y2) and C (x3, y3).

AREA OF THE TRIANGLE

=

CENTROID OF THE TRIANGLE

The centroid G is the point of intersection of medians AD, BE and CF, which are the lines joining a vertex with the midpoint of opposite side.

The coordinates of the centroid G are

INCENTRE OF THE TRIANGLE

The incentre I is the centre of circle touching the sides of the triangle internally, called INCIRCLE and it is the point of intersection of the internal bisectors. AP, BQ, CR of the vertex angles.

The coordinates of incentre I are given by

,

where a = BC, b = CA and c = AB are the sides of the triangle.

EXCENTRES OF THE TRIANGLE

The excentre I1 is the centre of the circle touching AB and AC produced and BC externally, called EXCIRCLE and it is the point of intersection of the internal bisector of angle A and the external bisectors of angles B and C.

The coordinates of the excentre I1, are given by

There are two more excentres, I2 & I3 one each opposite to vertices B and C.

Their coordinates are respectively
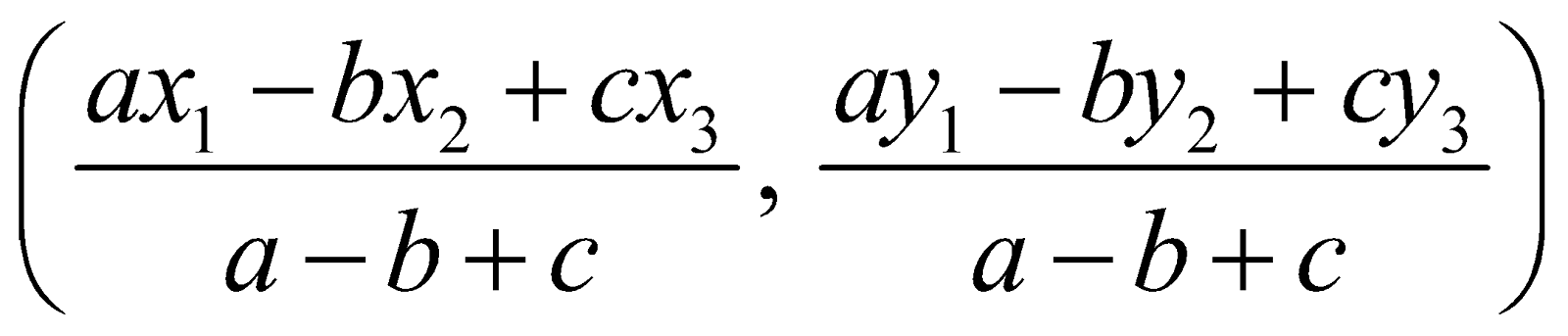and.

CIRCUMCENTRE OF THE TRIANGLE

The circumcentre O is the centre of the circle passing through the vertices of triangle, called CIRCUMCIRCLE and it is the point of intersection of perpendicular bisectors of the sides of triangle. Thus, we have OA = OB = OC

The above relation leads to two equations for the coordinates of O if coordinates of A, B and C are given.

Circumcentre of a right angled triangle is the mid points of its hypotenuse.

CONDITIONS OF COLLINEARITY OF THREE POINTS

Let A (x1, y1), B (x2, y2) and C(x3, y3) be three points.
They lie on the same line (i.e. collinear) if

1. 

OR

2. B divides AC in a particular ratio

OR

3. Area of ΔABC is zero.

i.e.

  OR

4. Slope of the lines joining A to B, B to C and C to A are numerically equal, i.e.

Note :

• The method (4) is helpful for the check of collinearly of more than three points and can be extended to any number of collinear points.
• The formula for finding the slope will be discussed later.

AREA OF A POLYGON

To find the area of a polygon, the coordinates of whose vertices are known, we divide the polygon into disjoint triangles and add the areas of these triangles. Thus the area of pentagon ABCDE = area of triangle BCD + area of triangle ABD + area of triangle ADE.

Conditions for a given Quadrilateral to be Parallelograms

Let ABCD is a quadrilateral, the coordinates of whose vertices are known. Then

1. ABCD is a parallelogram if the opposite sides are equal OR the diagonals bisect.
2. ABCD is a rectangle if the opposite sides are equal and the diagonals are equal OR the diagonals bisect and equal.
3. ABCD is a rhombus if all the sides are equal but diagonals are unequal OR the diagonals bisect and perpendicular.
4. ABCD is a square if all the sides are equal and diagonals are also equal OR the diagonals bisect, equal and perpendicular.

LOCUS

When a variable point P (x, y) moves under certain conditions then the path traced out by the point P is called the LOCUS of the point. For example,

1. Locus of a point P, which moves such that its distance from a fixed point C is always constant, is a CIRCLE.

2. Locus of a point P, which moves such that its distances from two fixed points A and B are always equal, is a STRAIGHT LINE, which is perpendicular bisector of AB.

3. The locus of a point P which moves such that the sum of its distances from two fixed points A and B is always constant, is an ELLIPSE.

4. The locus of a point P, which moves such that the difference of its distances from two fixed points A and B is always constant, is a HYPERBOLA.

5. The locus of a point P, which moves such that its distance from a fixed point S is always equal to its distance from a fixed straight line ZZ', is a PARABOLA.

EQUATION OF A LOCUS

Suppose that a point P (x, y) satisfies a specified set of conditions. We may establish a relationship between its abscissa x and the ordinate y. This relationship will always be satisfied by the coordinates of all points of the locus and by no other point. Such a relationship between x and y is called an equation of the locus.

STRAIGHT LINE

SLOPE OF A STRAIGHT LINE

The angle θ formed by the straight line L with the positive direction of x-axis and measured counterclockwise is called the INCLINATION of the line L. Obviously.

If θ is the inclination then tan θ is defined as the slope of the straight line L and denoted by m. Thus

Slope of the line L, m = tan θ,.

Clearly, the slope of any line parallel to y-axis is not defined.

Again, if , then m > 0 and if then m < 0.

SLOPE OF A LINE JOINING TWO POINTS

If a non-vertical line passes through two distinct points A (x1, y1) and B(x2, y2), then the slope of this line AB is given by

INTERCEPTS OF A LINE ON THE COORDINATE AXES

Suppose that a line L cuts the coordinate axes in the points A and B respectively. Let A (a, 0) and B (0, b). Then

x - intercept = OA = a

y - intercept = OB = b

EQUATIONS OF STRAIGHT LINE

A linear equation of the form ax + by + c = 0 always represents a straight line.

The equation of x-axis is y = 0.

The equation of y-axis is x = 0.

The equation of a straight line parallel to x-axis at a distance b from it is y = b.

The equation of a straight line parallel to y-axis at a distance a from it is x = a.

SLOPE-INTERCEPT FORM

If m be the slope of a line, which cuts an intercept c on axis of y, then the equation of the line is y = mx + c.

POINT-SLOPE FORM

The equation of straight line, which has slope m and passes through a fixed point A (x1, y1), is y – y1 = m (x – x1)

From this we have

The equation of a line through the point (x1, y1) and parallel to x-axis is y = y1.

The equation of a line through the point (x1, y1) and parallel to y-axis is x = x1.

TWO POINT FORM

The equation of the line through two given points A(x1, y1) and B (x2, y2) is  

INTERCEPT-INTERCEPT FORM

The equation of a straight line, which made a and b, intercepts on x-axis and y-axis respectively is.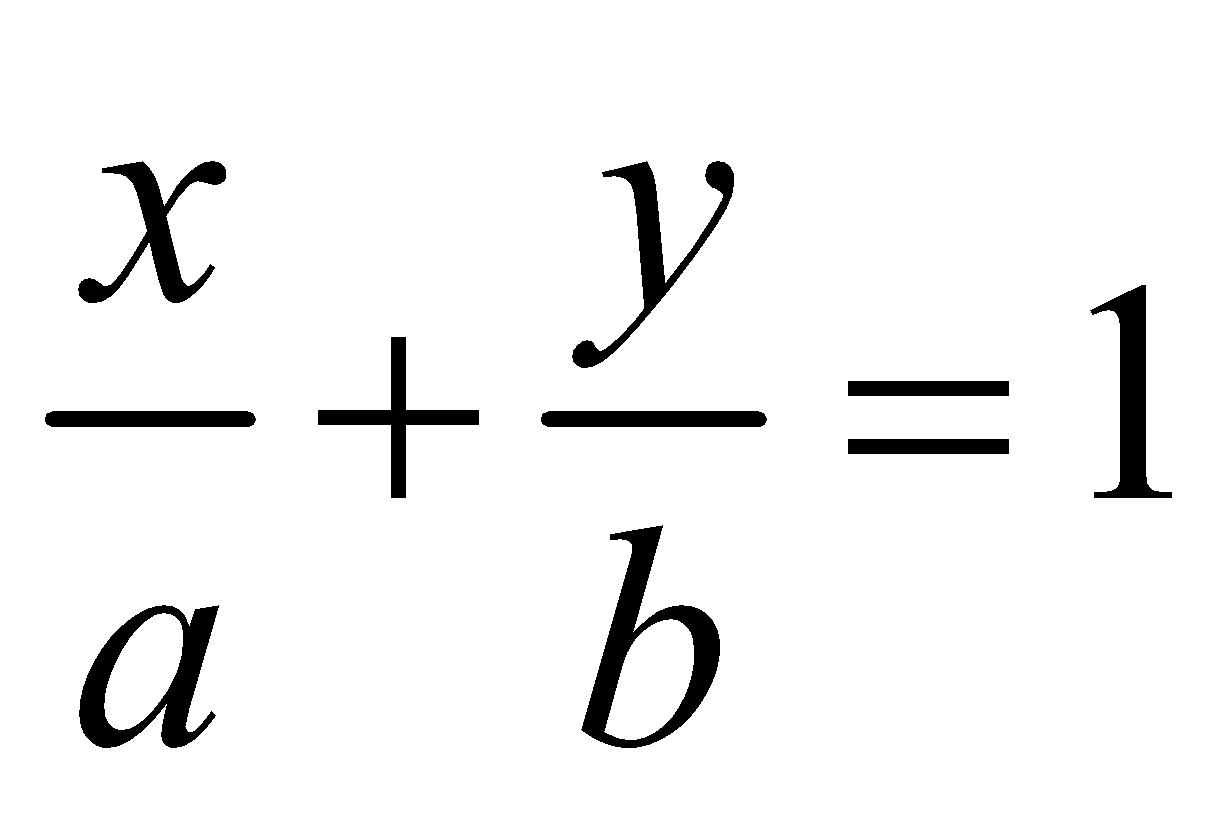

NORMAL FORM OF A STRAIGHT LINE

The equation of the straight line on which the length of perpendicular from the origin is p and the angle which this perpendicular makes with the x-axis is α is  

This coordinates of foot of perpendicular N are (pcosα, psinα) and the slope of the line is .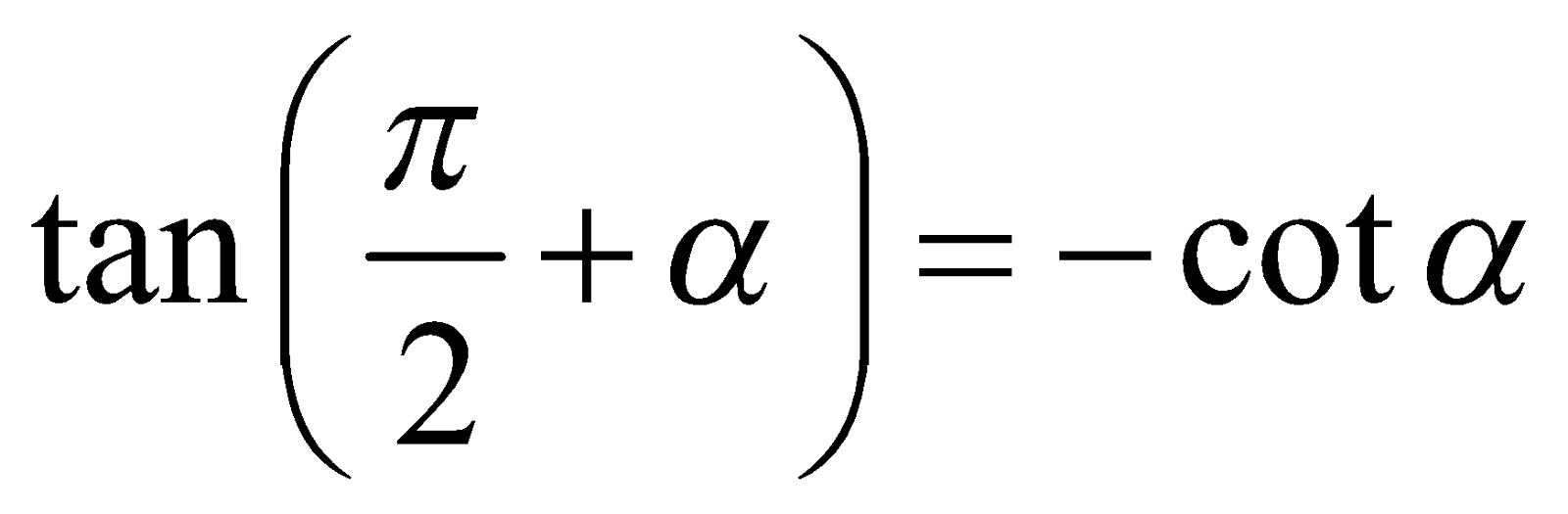

PARAMETRIC FORM (OR SYMMETRIC FORM OR DISTANCE FORM)

A straight line passing through a fixed point A (x1, y1) and inclined at an angle θ to x-axis may also be given by

IMPORTANT POINTS

1. 'r' is called the parameter and represents the distance of the variable point P(x, y) from the fixed point A(x1, y1).
2. 'r' is positive for all points lying on one side of the given point A and negative for all points lying on the other side of the point A.
3. The coordinates of any point on such a line may be written as (x1 + r cos θ, y1 + r sin θ), where r is the distance of this point from the given point A (x1, y1).
4. This form of the line is very important and will be almost invariably used if the problem involves a distance from a fixed point.

GENERAL FORM OF THE EQUATION OF A STRAIGHT LINE

A general linear equation ax + by + c = 0, provided a and b are not both zero simultaneously, always represents a straight line.

We represent ax + by + c by L(x, y). Thus the general form of the equation of straight line is

ax + by + c = 0  or L(x, y) = 0 ....(i)

DIFFERENT CASES

1. If and a = 0, then the equation (i) becomes by + c = 0, which is a line parallel to x-axis.
2. If b = 0 and, then the equation (i) becomes ax + c = 0, which is a line parallel to y-axis.
3. If , , the equation (i) may be written as . Thus the slope of the line is .
4. If , ,  the equation (i) may be written as

Thus, the x-intercept of the line is and the y-intercept of the line is .

5. Divide the equation (i) by, we get,

6. It represents the normal form of the straight line provided the term is negative thus the equation must always be written such that c is negative.

RESULTS RELATED TO A POINT AND A STRAIGHT LINE

1. Position of a given point Relative to a Given Line

Let the given line be ax + by + c = 0 or L(x, y) = 0.

A point P (x1, y1) will lie above or below this line according as is positive or negative.

That is, if , P lies above the line and if ,  P lies below the line,

where L(x1, y1) = ax1 + by1 + c.

2. The perpendicular distance of the point P(x1, y1) from the given line

3. Coordinates of foot of perpendicular N(h, k) from the point P(x1, y1) on the line L (x, y) = 0 may be given by

4. Coordinates of the image of Q(x2, y2) of the point P(x1, y1) in the line mirror L(x, y) = 0 may be given by

RESULTS RELATED TO TWO POINTS AND A STRAIGHT LINE

1. The ratio in which the join of two given points P(x1, y1) and Q (x2, y2) is divided by the straight line ax + by + c = 0 or L (x, y) = 0 is given by

If the above result comes out to be negative, it indicates an external division.

2. The relative position of the points P and Q with respect to the line may be expressed as following :

If, both the points lie to the same side of the given line.

If, the points lie in opposite sides of the given line.

RESULTS RELATED TO TWO STRAIGHT LINES

Suppose that

a1x + b1y + c1 = 0 or L1 (x, y) =0 ....(i)

and a2x + b2y + c2 = 0   or L2 (x, y) = 0 ....(ii)

be two straight lines.

POINT OF INTERSECTION

Point of intersection of the two given straight lines can be found by solving equations (i) and (ii).

Thus,, provided .

That is the point of intersection of the lines is, provided .

If, then the straight lines L1 and L2 are parallel and distinct.

If, then the straight lines L1 and L2 are coincident.

ANGLE BETWEEN TWO STRAIGHT LINES

If the slope of two straight lines be m1 and m2 then the acute angle (θ) between the lines is given by .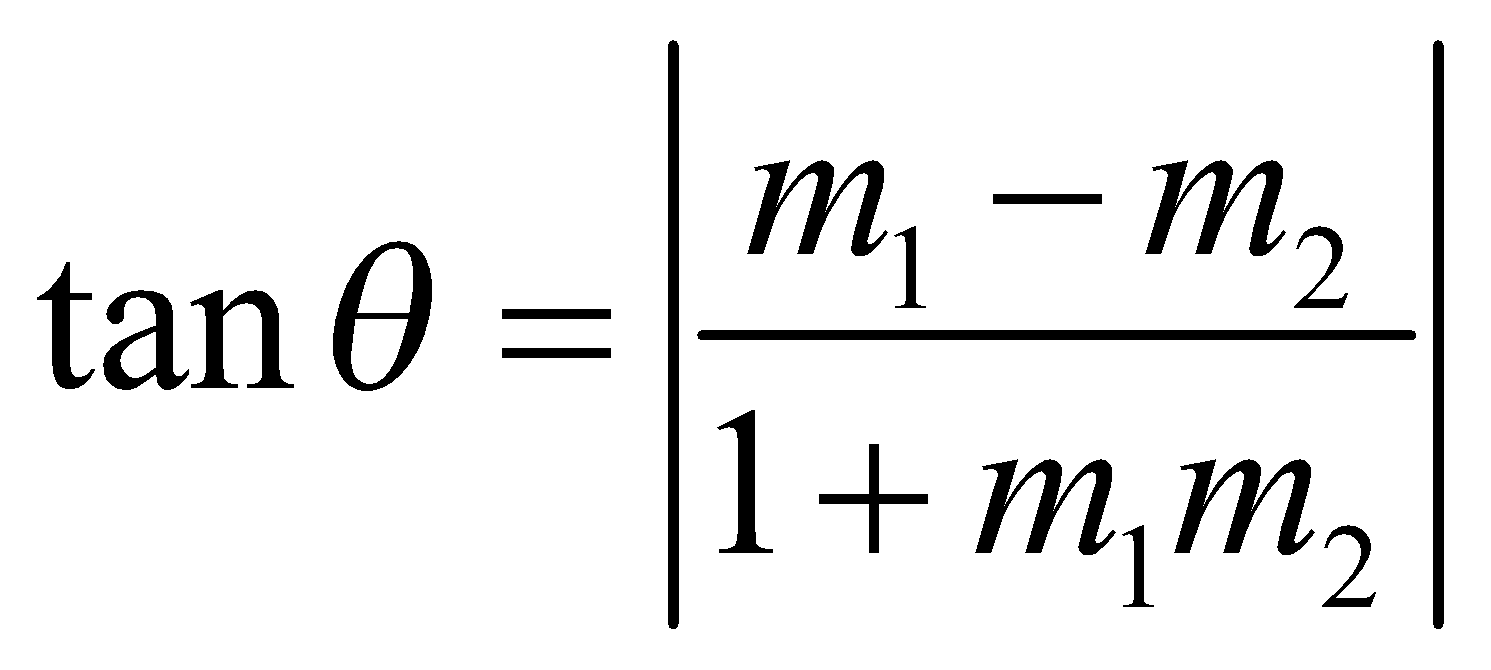

The lines are parallel if m1 = m2.

The lines are perpendicular if 1 + m1m2 = 0

Thus, for the lines given above by equation (i) and (ii), we get

• angle (θ) between them
• the lines are parallel if
• the line are perpendicular if

IMPORTANT RESULTS

1. Equation of straight lines through a given point P (x1, y1) and inclined at an angle θ to a given line y = mx + c are

and

2. Angle of a straight line y = mx + c with y-axis or a line parallel to y-axis may be given by.

3. Any line parallel to a given straight line ax + by + c = 0 is given by ax + by + k = 0, where k is to be determined from given conditions.
4. Any line perpendicular to a given straight line
   ax + by + c = 0 is given by bx – ay + k = 0, where k is to be determined from given conditions.
5. The distance between two parallel lines ax + by +c1 = 0 and ax + by + c2 = is given by.
6. Area of a parallelogram equations of whose sides are given, can be obtained by using the following formula

Area =

where p1 = DL = distance between lines AB and CD.

p2 = BM = distance between lines AD = BC

θ = angle between adjacent sides AB and AD

In the case of a rhombus, p1 = p2. Thus,

Area of rhombus =

Also, area of a parallelogram = d1 d2 sinφ

where d1 and d2 are lengths of two diagonals of the parallelogram and φ is angle between them. In case of a rhombus, φ = 90º, so area = d1 d2

ANGULAR BISECTORS OF TWO GIVEN LINES

Let the equations of two given lines be

a1x + b1y + c1 = 0 or L1 (x, y) = 0

and  a2x + b2y + c2 = 0 or L2 (x, y) = 0

The equations of the bisectors of the angle between two lines is given by

The above equations represent two equations, one of which is acute angle bisector and the other is obtuse angle bisector. To distinguish between them we find the tangent of angle (tan θ) between any one line and any one of the bisectors.

If , the selected bisector is acute angle bisector and the other one is obtuse angle bisector.

If , the selected bisector is obtuse angle bisector and the other one is acute angle bisector.

ALTERNATE :

If the equations of L1 and L2 be written such that their constant terms c1, c2 be both positive or both negative, the +ve sign in equation of bisectors will correspond to the equation of the angular bisector of the angle containing the origin, while the –ve sign in equation will correspond to the equation of the angular bisector of the angle which does not contain the origin.

Further, if the equations of L1 and L2 be written such that c1, c2 both have same signs, then

a1a2 + b1b2 < 0 ⇒ angle containing the origin is acute and

a1a + b1b2 > 0 ⇒ angle containing the origin is obtuse.

Using the above result, the two angular bisectors can easily be distinguished.

Example :

Find the acute angle bisectors of the lines 2x + 3y + 7 = 0 and 3x – 4y – 5 = 0

Solution :

Rewrite the given equations so as to make both the constant terms positive,

i.e. 2x + 3y + 7 =0

and –3x + 4y + 5 = 0

The equation of the angular bisectors are

...(1)

Now, since (2) (–3) + (3) (4) > 0, therefore it implies that the angle containing the origin is obtuse.

Hence, the +ve sign in equation (1) corresponds to the obtuse angle bisector while the –ve sign corresponds to the acute angle bisector. (Also see the illustration 4)

TO FIND ORTHOCENTRE OF A TRIANGLE

Let AL, BM and CN be the perpendiculars from the vertices A, B and C to the opposite sides (also called ALTITUDES). These are concurrent and the point of concurrency H is called ORTHOCENTRE of the triangle.

It can be obtained by writing the equations of any two altitudes and then solving these two equations.

Note that the orthocentre of a right angle triangle ABC, right angled at B is the vertex B itself.

CONDITION OF CONCURRENCY OF THREE LINES

Let the equations of three given lines be

, and

These three lines are concurrent, i.e., they pass through a common point if

1. Point of intersection of any two lines lies on the third

OR

2. The coefficients of the equations of the three lines satisfy the determinant,

OR

3. Three non-zero constants λ, μ, ν are be found such that .

FAMILY OF STRAIGHT LINES

1. The family of parallel lines is given by y = mx + c, where m is constant and c is variable.
2. The family of concurrent lines is given by, where m is variable and x1, y1 are constant.
3. The family of lines passing through the point of intersection of two straight lines and   is or , where λ is variable.
4. The equation ax + by + c = 0 represents a family of concurrent lines if a relation between the coefficients of the form exists, where. The point of concurrency is

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT