PARABOLA
SECTIONS OF A CONE
The curves like circle, parabola, ellipse and hyperbola can be obtained by cutting a right circular cone by a plane. A right circular cone is the surface generated by revolving a straight line in such a way that it always passes through a fixed point A. The fixed point A, called the VERTEX separates, the surface into two parts called NAPPES. Such a straight line through A is called a GENERATOR or ELEMENT of the cone. The straight line through A about which the cone is symmetrical is called the AXIS of the cone. Angle α is called the semi-vertical angle.
Consider a plane P intersecting a right circular cone as per following situations :
CASE (1) : The cutting plane is normal to the axis of cone. The curve of intersection is a CIRCLE.
CASE (2) : The cutting plane is inclined to the axis at an angle θ, such that α < θ < 90°. The plane intersects only one nappe and the curve of intersection is an ELLIPSE.
CASE (3) : The cutting plane is parallel to generator, i.e., θ = α. The ellipse of case (2) is now infinitely long. This curve of intersection is called a PARABOLA.
CASE (4) : The cutting plane is inclined such that θ < α. The plane then intersects both the nappes and the curve of intersection is a HYPERBOLA. A hyperbola consists of two branches.
If the plane of intersection passes through the vertex A, the section of cone are called DEGENERATE CURVES, which are a PAIR OF STRAIGHT LINES, which become coincident if the plane is parallel to the generator and we get a single point if the plane does not intersect the cone.
ANALYTICAL DEFINITION OF A CONIC SECTION OR CONIC
The locus of a point P which moves such that its distance from a fixed point is always in a constant ratio to its perpendicular distance from a fixed straight line, is called a CONIC SECTION.
The equation of the required locus is
SP = e × PM
i.e. 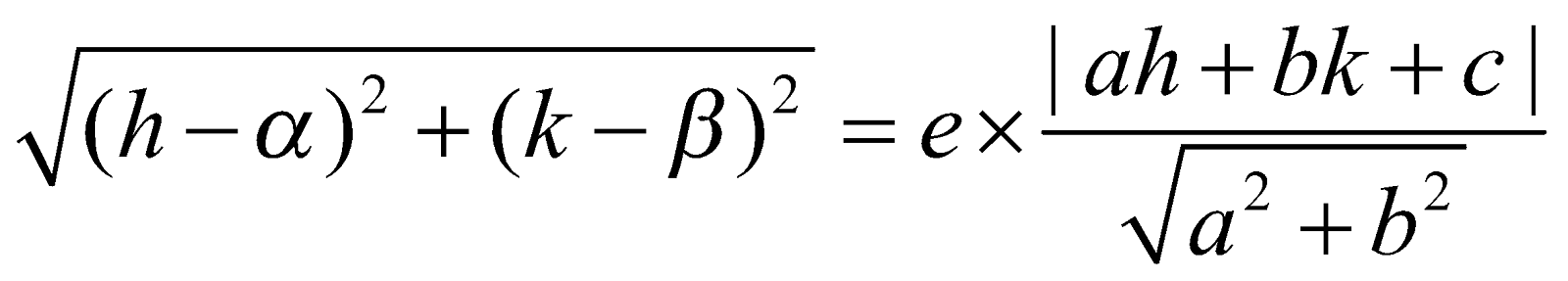
Hence, the locus of P(h, k) is
which is the equation of a conic section
- The fixed point is called the Focus and is usually denoted by S.
- The constant ratio is called the Eccentricity and is denoted by e.
- The fixed straight line ZZ' is called the Directrix.
- The straight line passing through the Focus and perpendicular to the Directrix is called the Axis.
The Conic Sections have different names for different values of e.
- When e is equal to unity, it is called a Parabola.
- When e is less than unity, it is called an Ellipse.
- When e is greater than unity, it is called a Hyperbola.
The point of intersection A of the conic with its axis is called VERTEX.
The equation (1) on expanding and simplifying takes the following form
which is the general equation of second degree.
The equation (ii) under different conditions represents a pair of straight lines, circle, parabola, ellipse or hyperbola.
CONDITIONS FOR REPRESENTATION OF VARIOUS TYPE OF CONICS
Consider the general equation of second degree
The discriminant of equation (i) is
Case 1 : If Δ = 0, then the equation (1) represents a Degenerate Conic which is
- A pair of parallel straight lines or empty set if ab – h2 = 0
- A pair of intersecting straight lines if ab – h2 < 0
- A pair of perpendicular lines if ab – h2 < 0 and a + b = 0
- Imaginary lines if ab – h2 > 0
Case 2 : If  , then the equation (2) represents a Non-Degenerate Conic, which is
, then the equation (2) represents a Non-Degenerate Conic, which is
- A circle, if h = 0 and a = b
- A parabola, if ab – b2 = 0
- An ellipse or empty set, if ab – h2 > 0
- A hyperbola, if ab – h2 < 0
- A rectangular hyperbola, if ab – h2 < 0 and a + b = 0
Centre of Conic Section represented by Equation (ii)
The partial differentiation method used for finding the point of intersection in case of pair of straight lines can be used identically to find the centre of a conic section. Hence the point which represent the point of intersection in case equation (ii) represents a pair of straight lines turns out to be the centre in case equation (ii) represents a circle, an ellipse or a hyperbola. The centre of a parabola lies at infinity.
PARABOLA - THE STANDARD EQUATION
The standard equation of a parabola is , where a is a positive constant. This parabola has
, where a is a positive constant. This parabola has
- Focus S at (a, 0)
- Directrix is x + a = 0, Axis is x-axis or y = 0
- Vertex A is at (0, 0)
Therefore according to definition of Parabola
Other Definitions :
- Focal Chord : A chord of parabola PSQ, which passes through the focus is called focal chord.
- Focal Distance : The distance of a point P on the parabola from the focus S is called focal distance.
For a point P(x1, y1) on the parabola, the focal distance
PS = PM = a + x1
- Double Ordinate : A chord of the parabola which is perpendicular to axis is called a double ordinate.
PP' is the double ordinate in the figure. It is bisected at the axis.
Thus if P is (x1, y1) then double ordinate PP' = 2y1 and the coordinates of P' are (x1, –y1).
- Latus Rectum : The double ordinate LSL' passing through the focus of the parabola is called its latus rectum.
- The equation of the latus rectum is x = a or x – a = 0
- The coordinates of extremities are L (a, 2a) and L' (a, –2a).
- The length of latus rectum = 4a
- Tangent at Vertex : The axis of y or x = 0 is the tangent to the parabola at its vertex A (0, 0)
PARAMETRIC EQUATION OF PARABOLA
x = at2, y = 2at, t ∈ R always satisfy the equation of parabola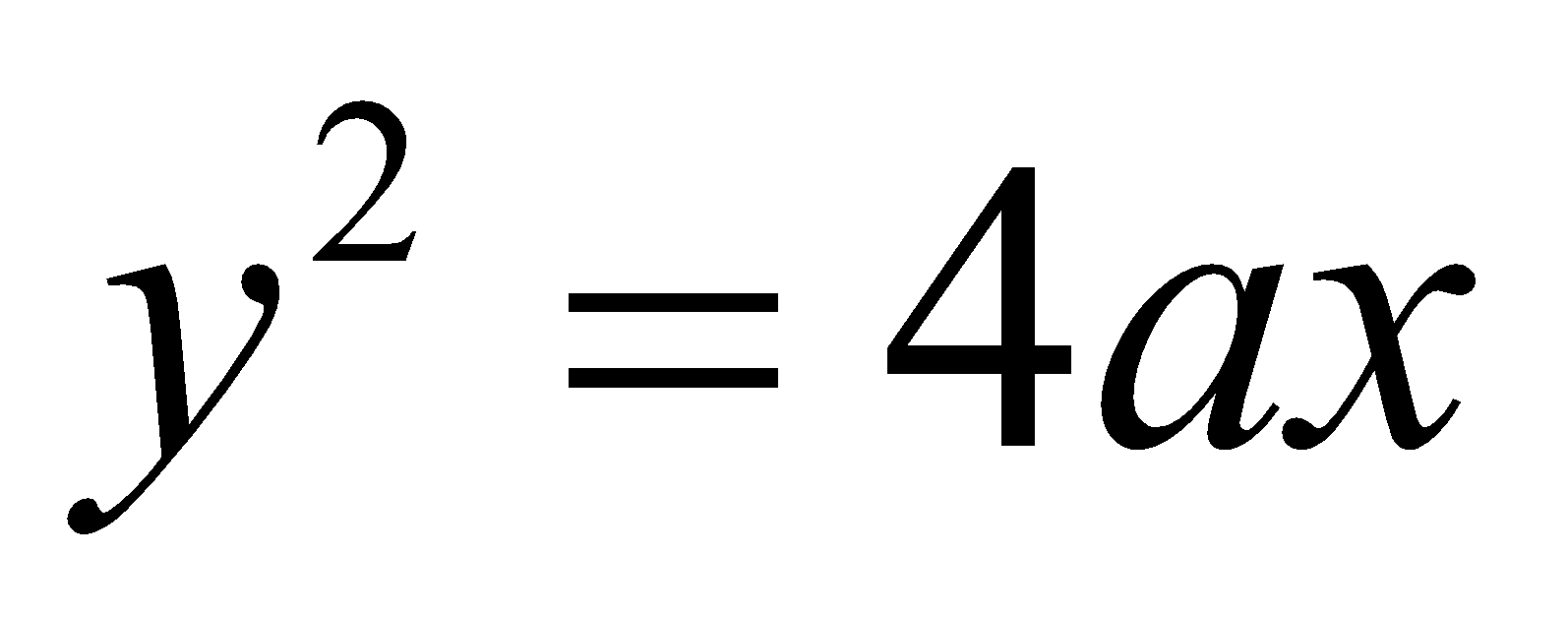 .
.
Thus x = at2, y = 2at simultaneously represent the parametric equation of parabola , t being parameter.
, t being parameter.
Any point on the parabola may be taken as (at2, 2at). It is called the parametric coordinates of any point on parabola written as point 't'.
OTHER STANDARD FORMS OF PARABOLA
Depending on the direction of concavity of the parabola four important forms of equation of parabola with same latus rectum 4a and the same vertex A (0, 0) can be given as follows :
RIGHT HANDED PARABOLA
The equation of this type of parabola is of the form y2 = 4ax, a > 0
For this parabola :
- Vertex : (0, 0)
- Focus : (a, 0)
- Directrix : x + a = 0
- Latus rectum : 4a
- Axis : y = 0
- Symmetry : It is symmetric about x-axis.
LEFT HANDED PARABOLA
The equation of this type of parabola is of the form y2 = –4ax, a > 0
For this parabola :
- Vertex : (0, 0)
- Focus : (–a, 0)
- Directrix : x – a = 0
- Latus rectum : 4a
- Axis : y = 0
- Symmetry : It is symmetric about x-axis.
UPWARD PARABOLA
The equation of this type of parabola is of the form x2 = 4ay, a > 0.
For this parabola :
- Vertex : (0, 0)
- Focus : (0, a)
- Directrix : y + a = 0
- Latus rectum : 4a
- Axis : x = 0
- Symmetry : It is symmetric about y-axis.
DOWNWARD PARABOLA
The equation of this type of parabola is of the form x2 = –4ay, a > 0
For this parabola :
- Vertex : (0, 0)
- Focus : (0, –a)
- Directrix : y – a = 0
- Latus rectum : 4a
- Axis : x = 0
- Symmetry : It is symmetric about y-axis.
PARABOLA WITH VERTEX NOT AT ORIGIN BUT AXIS PARALLEL TO COORDINATES AXES
- Parabola which has vertex at (h, k), latus rectum l and axis parallel to x-axis, is
Clearly axis is y = k and focus at 
- Parabola, which has vertex at (h, k), latus rectum l and axis parallel to y-axis, is
- Clearly, axis is x = h and focus at
- Parabola represented by the quadratic equation
We have 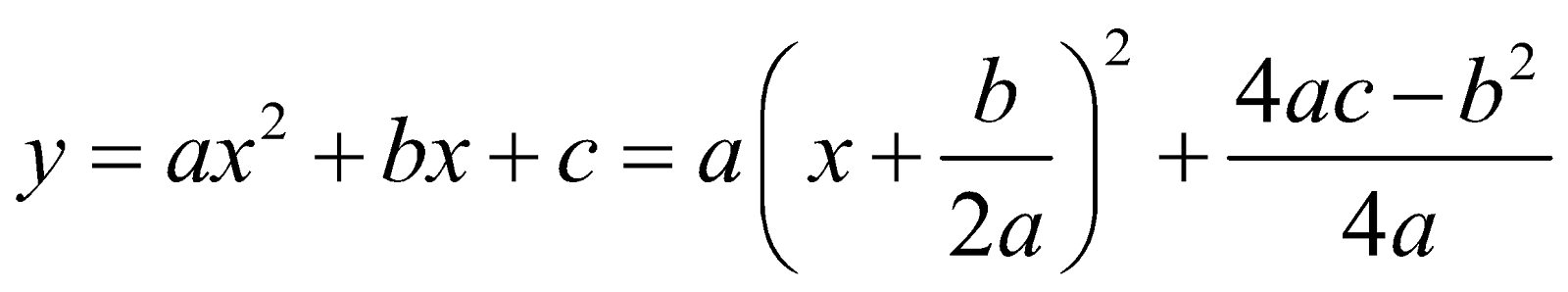
Which is clearly a parabola with vertex at 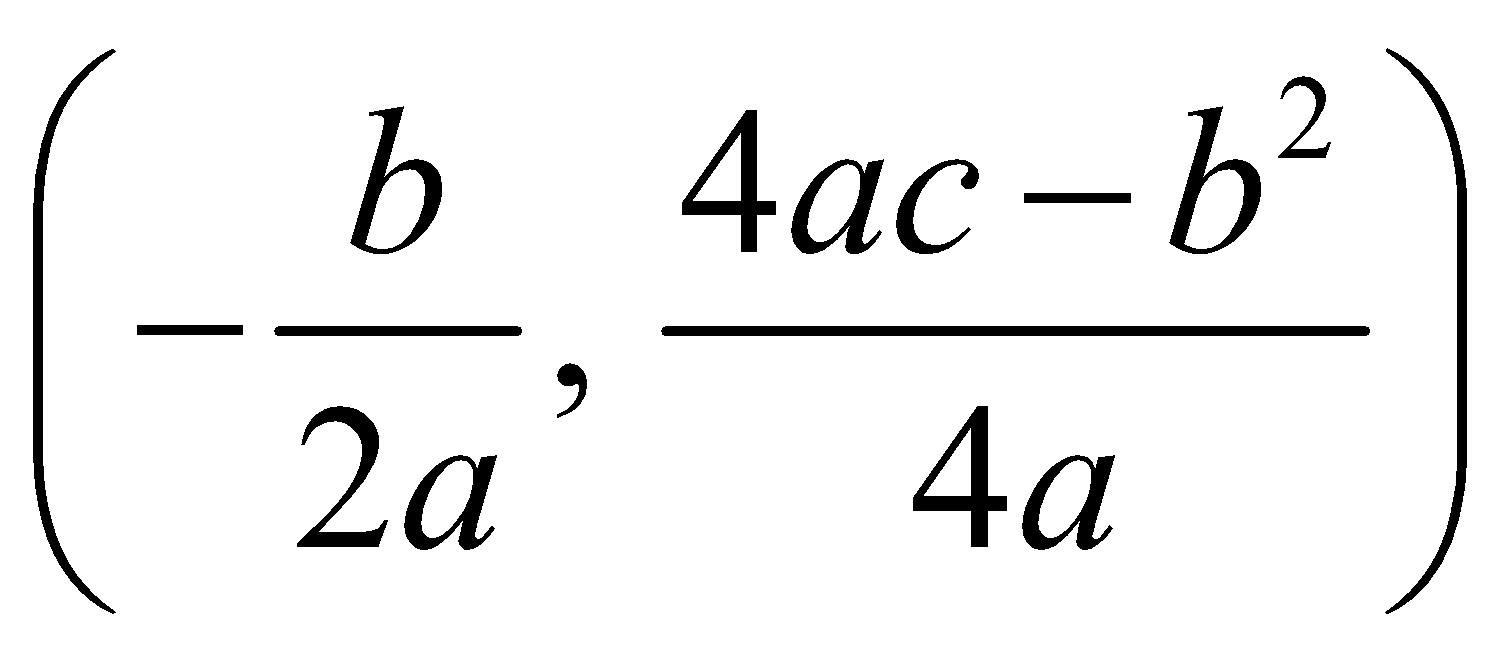 and axis parallel to y-axis.
and axis parallel to y-axis.
It is an upward parabola if a > 0. It is a downward parabola if a < 0.
Its focus, directrix, etc. can be obtained using shifting of origin.
POSITION OF A POINT P(x', y') RELATIVE TO A GIVEN PARABOLA
Let y2 = 4ax or y2 – 4ax = 0 be the given parabola represented by S (x, y) = 0.
- The point P(x', y') lies outside the parabola if y'2 – 4ax' > 0 or S (x', y') > 0
- The point P lies inside the parabola if S(x', y') < 0.
For example, the point (1, 1) lies inside the parabola y2 = 4x as 1 – 4.1 = –3 < 0
For example, the origin lies outside the parabola x2 + 6x + 4y + 1 = 0 as 0 + 0 + 0 + 1 = 1 > 0
INTERSECTION OF A STRAIGHT LINE AND A PARABOLA
Let y = mx + c be a straight line and y2 = 4ax be the parabola.
Then the length of chord cut on the line is given by
IMPORTANT RESULTS
- The straight line intersects the parabola in two distinct points if
.
- The straight line touches the parabola if
.
- The straight line neither touch nor intersect the parabola if
.
- The straight line y = mx + c touches the parabola
if
.
- The straight line
is always a tangent to the parabola y2 = 4ax for any value of m. The coordinates of point of contact are
.
- The equation of tangent to
may be given as
.
- The equation of tangent to
may be given as
.
EQUATION OF TANGENT TO A PARABOLA AT A POINT ON IT
- The equation of tangent to the parabola y2 = 4ax at a point (x', y') on it is yy' = 2a (x + x') or yy' – 2a(x + x') = 0, usually represented as T = 0. [For the method see circles]
- The equation of the tangent to the parabola y2 = 4ax at a point (at2, 2at) is ty = x + at2.
NUMBER OF TANGENTS DRAWN FROM A POINT TO A PARABOLA
Let  be a tangent to parabola drawn from the point P(x1, y1), then
be a tangent to parabola drawn from the point P(x1, y1), then
Which is quadratic in m so two tangents can be drawn to parabola from P, which are real and distinct if  i.e
i.e  or the point lies outside the parabola .The tangents coincide if
or the point lies outside the parabola .The tangents coincide if  and are imaginary if
and are imaginary if 
EQUATION OF THE PAIR OF TANGENTS
The equation of the pair of tangents drawn from a point P (x1, y1) to the parabola y2 = 4ax is SS1 = T2,
where S ≡ y2 – 4ax, S1 ≡ y12 – 4ax1 and T ≡ yy1 – 2a(x + x1)
CHORD OF CONTACT
The equation of chord of contact of tangents drawn from a point P(x1, y1) to the parabola y2 = 4ax is T = 0 where T ≡ yy1 – 2a(x + x1)
EQUATION OF CHORD OF A PARABOLA JOINING TWO POINTS
Let P(at12, 2at1) and Q (at22, 2at2) be two points on the parabola y2 = 4ax. Then the equation of the chord PQ is
IMPORTANT RESULTS
- The slope of chord joining the points 't1' and 't2' is
.
- If the chord joining the points 't1' and 't2' is a focal chord, then the point S(a, 0) must lie on (i).
Thus, 0. (t1 + t2) = 2a + 2at1t2 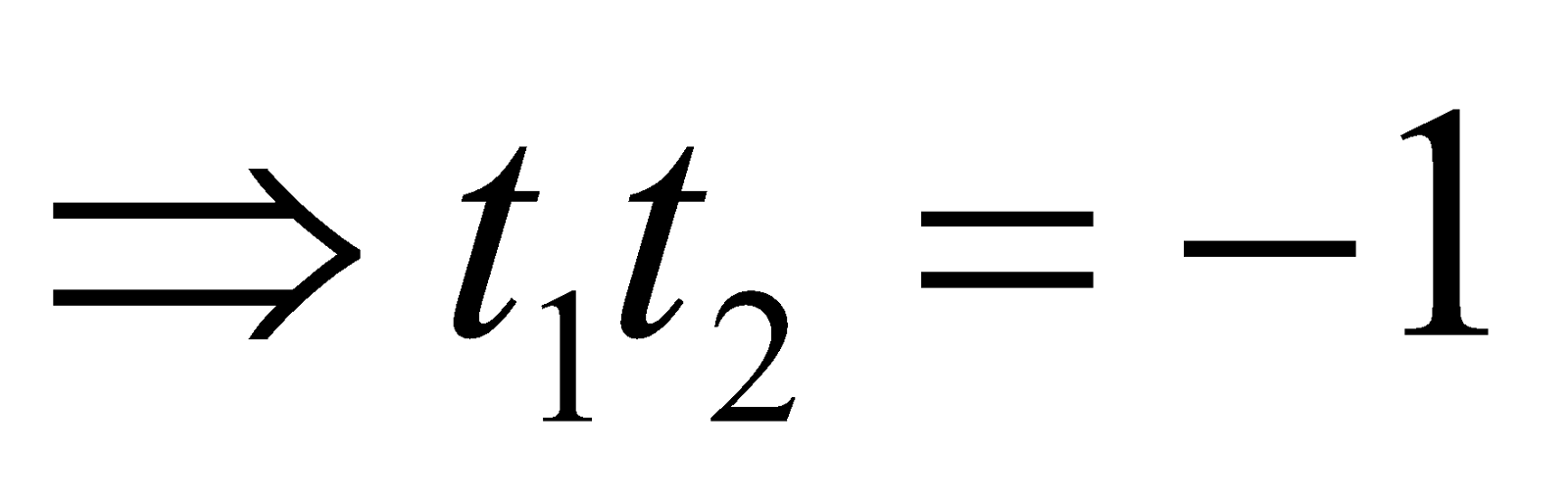
- The extremities of a focal chord may be given by
and
.
- The harmonic mean of the intercepts of the focal chord by the axis is semilatusrectum, i.e.
We have if P is (at2, 2at) then Q is  , for the extremities of focal chord.
, for the extremities of focal chord.
[See focal distance]
POINT OF INTERSECTION OF TANGENTS
The point of intersection of tangents drawn at two different points of contact P(at12, 2at1) and Q(at22, 2at2) on the parabola y2 = 4ax is
R ≡ (at1t2, a (t1 + t2))
IMPORTANT POINTS
- Angle between tangents at two points
and
on the parabola y2 = 4ax is
- The G.M. of the x-coordinates of P and Q (i.e
) is the x-coordinate of the point of intersection of tangents at P and Q on the parabola
- The A.M. of the y-coordinate of P and Q
is the y-coordinate of the point of intersection of tangents at P and Q on the parabola.
- The orthocentre of the triangle formed by three tangents to the parabola lies on the directrix
EQUATION OF CHORD WITH A GIVEN MIDPOINT
The equation of the chord of the parabola y2 = 4ax with P(x1, y1) as its middle point is given by T = S1
Where 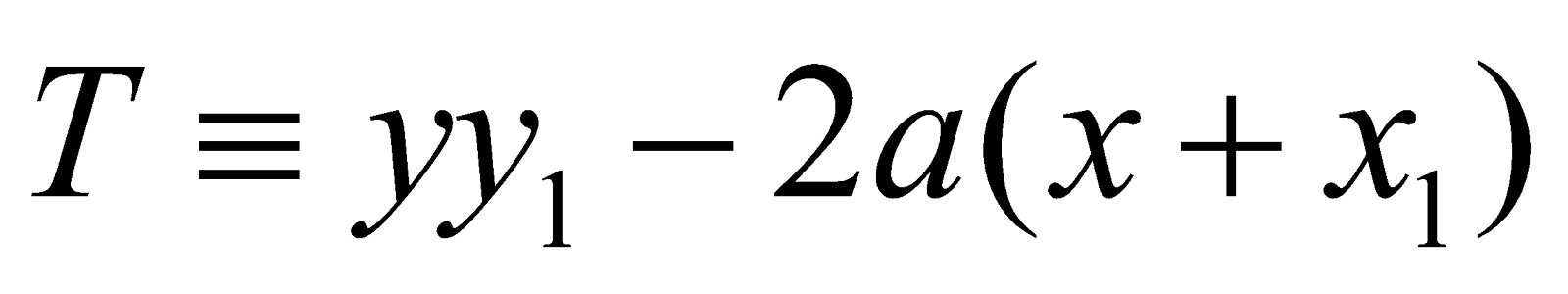 and
and 
EQUATION OF NORMAL IN DIFFERENT FORMS
- Point Form : The equation of the normal to the parabola
at a point (x1, y1) is
- Parametric Form : The equation of the normal to the parabola
at the point (at2, 2at) is
. Its slope is –t.
- Slope Form : The equation of normal to the parabola y2 = 4ax in terms of the slope 'm' is y = mx – 2am – am3
Note :
- The coordinate of the foot of normal are (am2, – 2am).
- The line y = mx + c is a normal to the parabola y2 = 4ax if c = – 2am – am3
POINT OF INTERSECTION OF TWO NORMALS
The point of intersection of normals drawn at two different points P(at12, 2at1) and Q (at22, 2at2) on the parabola y2 = 4ax is
Note :
- If the normal at the point P (at12, 2at1) meets the parabola y2 = 4ax again at Q (at22, 2at2), then
Note that PQ is normal to the parabola at P and not at Q.
- If the normals at the points (at12, 2at1) and (at22, 2at2) meet on the parabola y2 = 4ax, then t1t2 = 2
CO-NORMAL POINTS
Any three points on a parabola normals at which pass through a common point are called co-normal points. If three normals are drawn through a point (h, k), then their slopes are the roots of the cubic :
k = mh – 2am – am3
Thus,
- The sum of the slopes of the normals at co-normal points is zero. i.e m1 + m2 + m3 = 0
- The sum of the ordinates of the co-normal points is zero
(i.e. –2am1 – 2am2 – 2am3 = –2a(m1 + m2 + m3 ) = 0 - The centroid of the triangle formed by the co-normal points lies on the axis of the parabola [the vertices of the triangle formed by the co-normal points are (am12, –2am1), (am22, –2am2) and (am32, –2am3). Thus, y-coordinate of the centroid becomes
. Hence the centroid lies on the x-axis, i.e axis of the parabola.
- If three normals drawn to any parabolas y2 = 4ax from a given point (h, k) be real. Then h > 2a
Any ray parallel to the axis of the parabola after reflection from the parabola passes through the focus.
Let RP be a ray parallel to the axis of the parabola. Draw the normal PN at P then to prove the assertion it is sufficient to show that 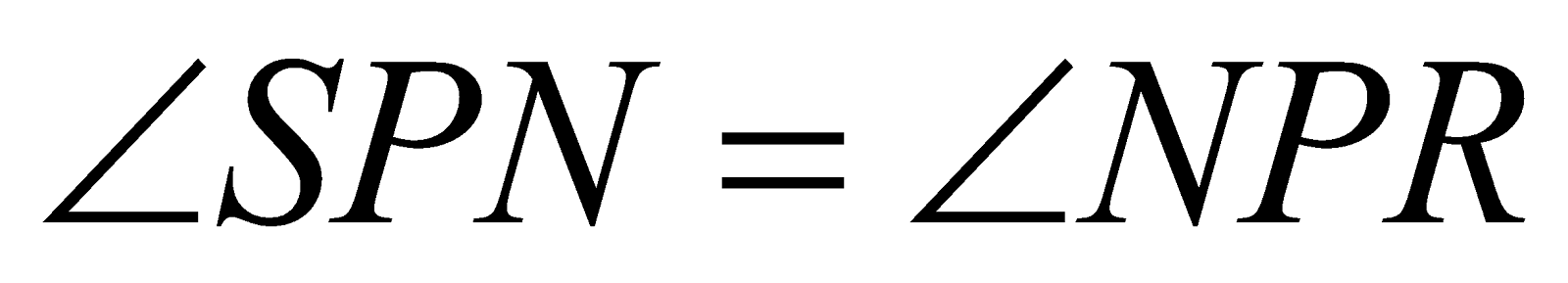
If P be (at2, 2at), then equation of normal PN is y + tx = 2at + at3
⇒ Slope PN = - t
Also slope PS = 
Thus







