PROBABILITY ADVANCED
CONDITIONAL PROBABILITY
Let A and B be two events associated with a random experiment. Then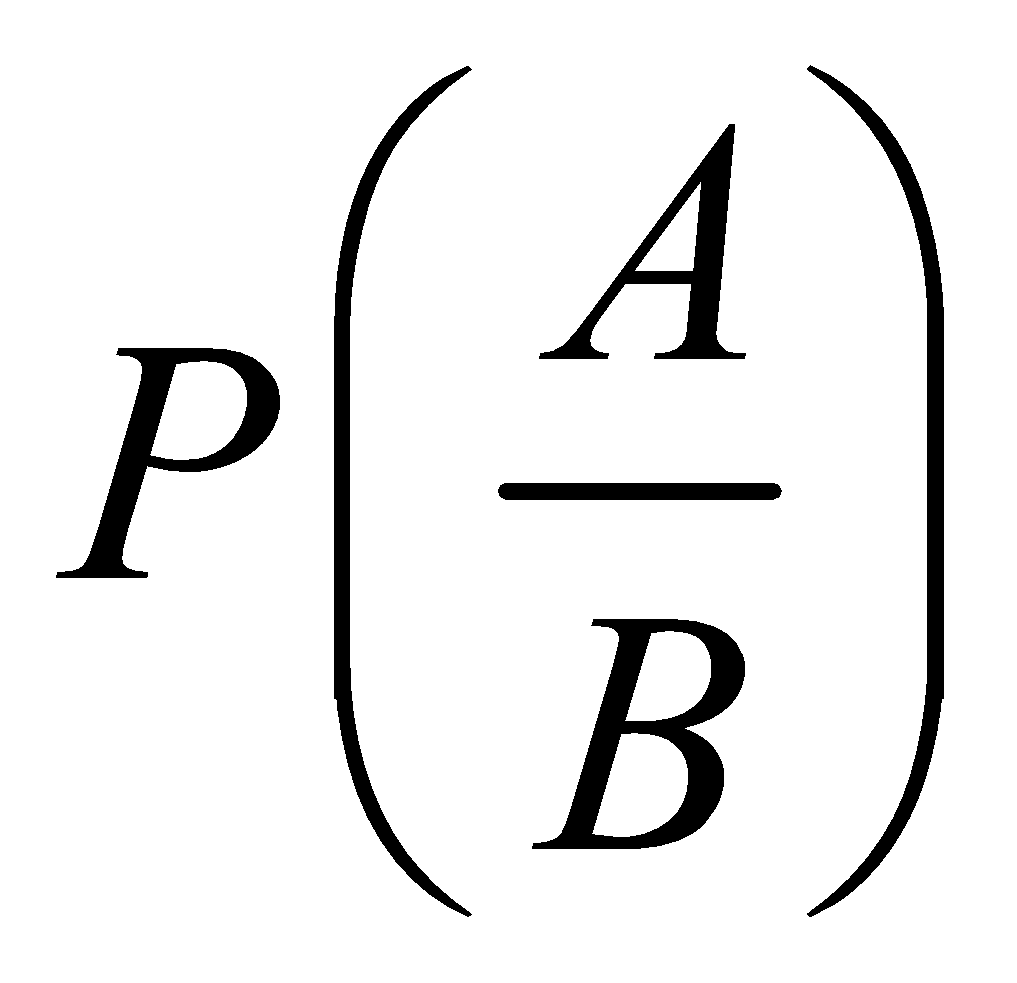
, represents the conditional probability of occurrence of A relative to B.
, represents the conditional probability of occurrence of A relative to B.
Example :
Suppose a bag contains 5 white and 4 red balls. Two balls are drawn one after the other without replacement. If A denotes the event “drawing a white ball in the first draw” and B denotes the event “drawing a red ball in the second draw”.
P (B/A) = Probability of drawing a red ball in second draw when it is known that a white ball has already been drawn in the first draw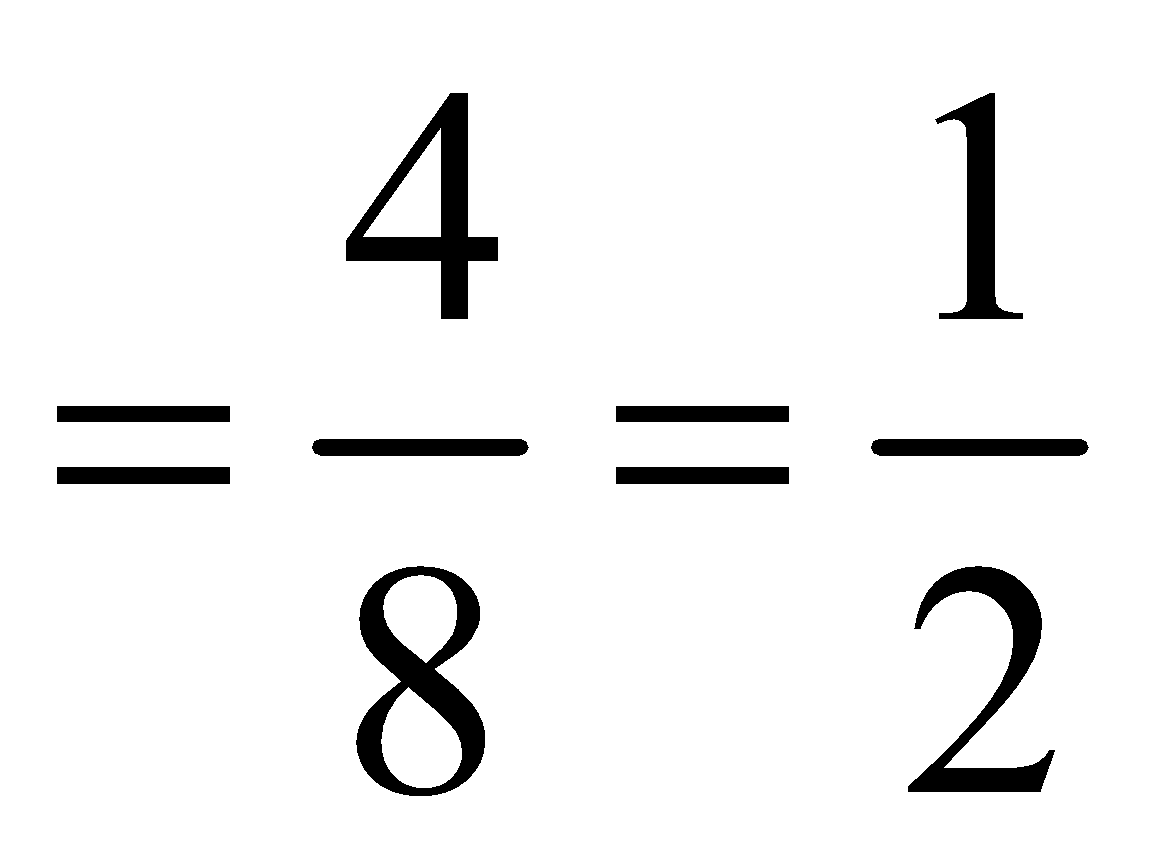 
Obviously, P (A/B) is meaningless in this problem.
INDEPENDENCE
An event B is said to be independent of an event A if the probability that B occurs is not influenced by whether A has or has not occurred. For two independent events A and B.
Event A1, A2, ........An are independent if
That is, the events are pairwise independent.
- The probability of simultaneous occurrence of (any) finite number of them is equal to the product of their separate probabilities, that is, they are mutually independent.
Example :
Let a pair of fair coin be tossed, here S = {HH, HT, TH, TT}
A = heads on the first coin = {HH, HT}
B = heads on the second coin = {TH, HH}
C = heads on exactly one coin = {HT, TH}
Then P (A) = P(B) = P (C) = 
Hence the events are pairwise independent.
Also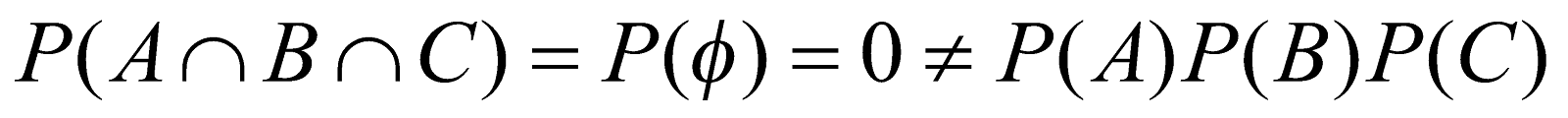 
Hence, the events A, B, C are not mutually independent.
ADDITION THEOREM FOR INDEPENDENT EVENTS
Let A1, A2, .....An are ‘n’ independent events, such that
P (Ai) = pi, i = 1, 2, ..... n, obviously
P
= 1 – pi ; i = 1, 2, .....,n.
= 1 – pi ; i = 1, 2, .....,n.
Now, probability of occurrence of at least one of the events
Example :
If A, B are two independent events, then to show that
(i) A,
are independent
are independent
(ii) 
are independent
are independent
(iii) 
are independent.
are independent.
Solution :
(i) We have 
(Proved)
(ii) Similar to (i)
(iii) 
(Proved)MULTIPLICATION THEOREM
If A and B are two events, then
= P (A) P (B/A), if P (A) > 0
= P (B) P (A/B) if P (B) > 0
From this theorem we get
and 
If A and B are two independent events, then
and 
therefore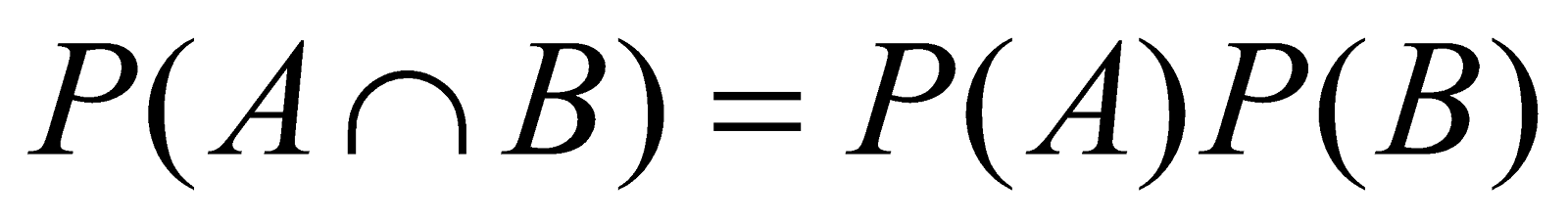 
Example :
Consider an experiment of throwing a pair of dice. Let A denotes the event “ the sum of the point is 8” and B event “ there is an even number on first die”
Then A = {(2, 6), (6, 2), (3, 5), (5, 3), (4, 4)},
B = {(2, 1), (2, 2), ......., (2, 6), (4, 1), (4, 2),.....
(4, 6), (6, 1), (6, 2),....(6, 6)}
Now, P(A/B) = Prob. of occurrence of A when B has already occurred = prob. of getting 8 as the sum, when there is an even number on the first die
= 
EXTENSION OF MULTIPLICATION THEOREM
If A1, A2,......An are ‘n’ events related to an experiment, then
where, 
represents the conditional probability that event Ai occurs, given that A1, A2, .....Ai –1 have already happened.
represents the conditional probability that event Ai occurs, given that A1, A2, .....Ai –1 have already happened.
If A1, A2, A3,.....An are independent event, then
REPEATED TRIALS
Let S be any finite probability space. By ‘n’ independent or repeated trials, we mean the probability space T consisting of ordered n-tuples of elements of S with the probability of an n-tuple defined to be the product of the probability of its components :
FINITE STOCHASTIC PROCESSES AND TREE DIAGRAM
A (finite) sequence of experiments in which each experiment has a finite number of outcomes with given probabilities is called a (finite) stochastic process. A TREE DIAGRAM can conveniently describe such a process. Using the multiplication theorem, the probability of the event represented by any given path of the tree can be computed.
Example : We are given three boxes as follows :
Box - I has 10 light bulbs of which 4 are defective.
Box - II has 6 light bulbs of which 1 is defective.
Box - III has 8 light bulbs of which 3 are defective.
We select a box at random and then draw a bulb at random. What is the probability P that the bulb is defective?
Solution : Here we perform a sequence of two experiments :
(i) Select one of the three boxes;
(ii) Select a bulb which is either defective (D) or non-defective (N).
The following tree describes the process and gives the probability of each branch of the tree
The probability that any particular path of the tree occurs is, the product of the probabilities of each branch of the path, e.g. the probability of selecting Box I and then a defective bulb is 
.
.
Thus required probability
THEOREM OF TOTAL PROBABILITY
If are ‘n’ mutually exclusive and exhaustive events such that P (Ai) > 0, for all i = 1, 2, ......, n and E is an event then
[A1, A2, ......, An are called partition of S]
Proof : Since A1, A2, A3, .......An are mutually exclusive events,
Therefore
are also mutually exclusive events, therefore,
are also mutually exclusive events, therefore, 
Thus, by multiplication theorem and addition theorem,
BAYE’S THEOREM
If A1, A2,......... An are ‘n’ mutually exclusive and exhaustive events in a sample space S and E is any event in S intersecting events Ai (i = 1, 2, .......n,) such that P (E) 0. Then
NOTE :
- The events A1, A2, ..........., An are usually referred to as HYPOTHESIS, and their probabilities P (A1), P (A2) ....... P (An) are known as “PRIORI PROBABILITIES” as they exist before we obtain any information from the experiment itself.
- The probabilities P (E /Ai), i = 1, 2, ......,n are called the
“ LIKELIHOOD PROBABILITIES” as they tell us how likely the event E under consideration occur, given each and every a “PRIORI PROBABILITY”. - The probabilities P (Ai/E), i = 1, 2, .... n are called “POSTERIORI PROBABILITIES” as they are determined after the results of the experiment are known.
RANDOM VARIABLES
- A random variable X on a sample space S is a function from S into the set R of real numbers such that the pre image of every interval of R is an event of S.
- We use the notation P (X = a) and
for the probability of the events “X maps into a” and “X maps in to the interval [a b].
DISTRIBUTION AND EXPECTATION OF A FINITE RANDOM VARIABLE
Let X be a random variable on a sample space S with a finite image set; say X(S) = {x1, x2 ......xn}.
Suppose the probability space be defined P (X = xi) for X = xi or simply pi. Then the function is called the distribution or probability function of X, usually written in the form of a table :
- for all i =1, 2 .... n
Now if X is a random variable with the above distribution, then the MEAN or EXPECTATION (or expected value) of X, denoted by E(X) or μx, (or E or μ), is defined by
E (X) = x1P1 + x2p2 + .... + xnpn = 
That is, E (X) is the “weighted average” of the possible values of X, each value weighted by its probability
In a gambling game, the expected value E of the game is considered to be the value of the game to the player. The game is said to be favourable to the player if E is positive and unfavourable if E is negative. If E = 0, the game is fair.
THEOREM
Let X and Y be random variables on the sample space S and ‘k’ are real number. Then
- E(kX) = k E (X)
- E (X + Y) = E (X) + E (Y)
VARIANCE AND STANDARD DEVIATION
The mean of a random variable X measures the “average” value of x (in a certain sense). The VARIANCE of X, measures the “spread” or “dispersion” of X.
Let X be a random variable
Then the “variance” of X, denoted by Var (X), is defined by
Var (X) = 
Where, μ is the mean of X. The “standard deviation” of X, denoted by σx is the (non-negative) square-root of Var (X)
THEOREM
For, 
=
which proves the theorem
BINOMIAL DISTRIBUTION
- We consider repeated and independent trials of an experiment with two outcomes; we call one of the outcomes “success” and the other outcome “failure”.
- Consider a random experiment. Let the occurrence of an event “E” in a trial be success (denoted by S) and its non-occurrence be failure (denoted by F).
Let the probability of a success in a trial be ‘p’ and that of a failure be ‘q’ then p + q = 1.
The probability of r-successes in ‘n’ trials in a specific order say (SSFSFF ......SF) is given by P (SSFSFF....SF) = P (S) P (S) P (F) P (S) P (F) .... P (S) P (F) = qn–r pr (by multiplication theorem)
where, there are r-Successes (S) and (n –r) Failures (F)
- But r-successes in n-trials can occur in mutually exclusive ways and probability of each of such way is qn–r pr. Therefore, by addition theorem,
The probability of r-successes in n-trials in any order is given by qn–r pr. If we define the random variable X to be “Number of Success”, then
r = 0, 1, 2, ......, n
The probability distribution of the random variable X is therefore given by
- We see that the probability distribution of the random variable X is given by the terms in the binomial expansion of (q + p)n. Thus we call the random variable X as Binomial Random Variable and the probability distribution of X as Binomial Distribution.
This distribution is also called Bernoulli Distribution and independent trials with two outcomes are called Bernoulli Trials
THEOREM
Let X be a random variable with the binomial distribution then
- E (X) = n p
E (X) = 
= 
= 
= 
= 
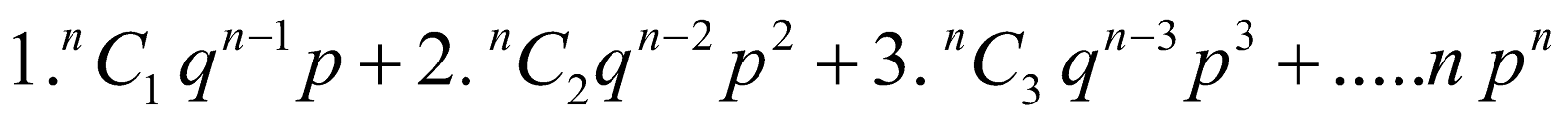
- Var (X) = n p q. Hence
.
= 
= 
= 
= 
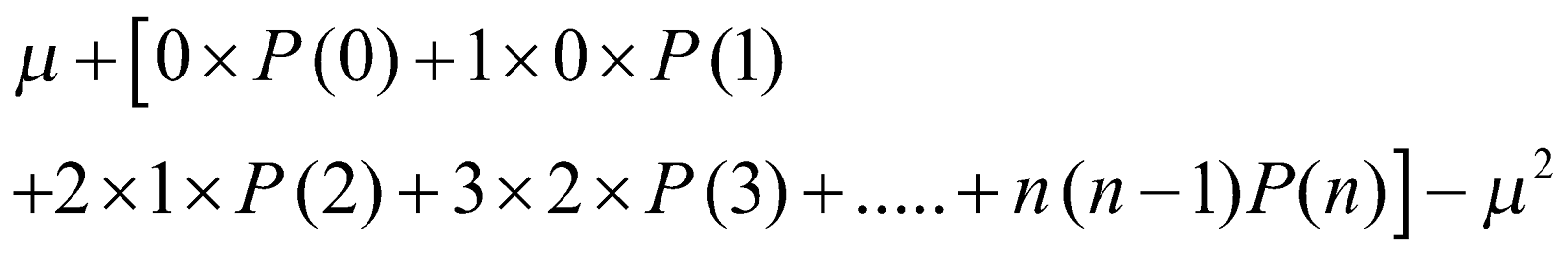
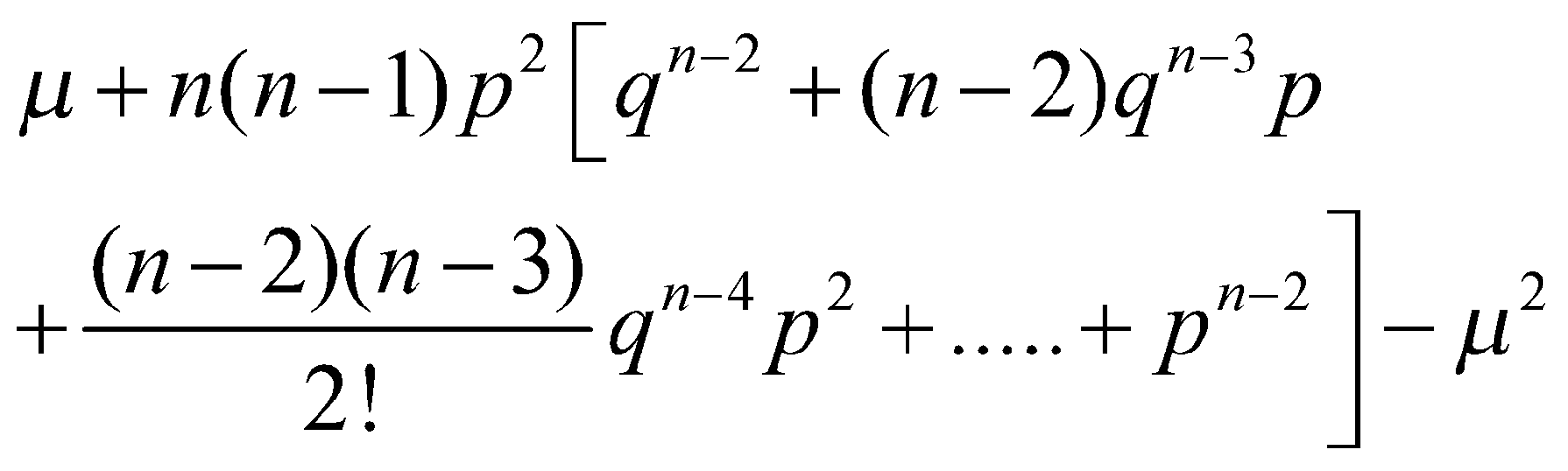
( μ = n p)
( μ = n p)
= 
Note : npq < np ( q < 1) So, VARIANCE < MEAN.
SYMMETRICAL BINOMIAL DISTRIBUTION
A binomial distribution is symmetrical if 
MODE OF BINOMIAL DISTRIBUTION
The mode of a binomial distribution is r if for X =r, the probability function p(X) is the maximum.
i.e. 
, and 
, and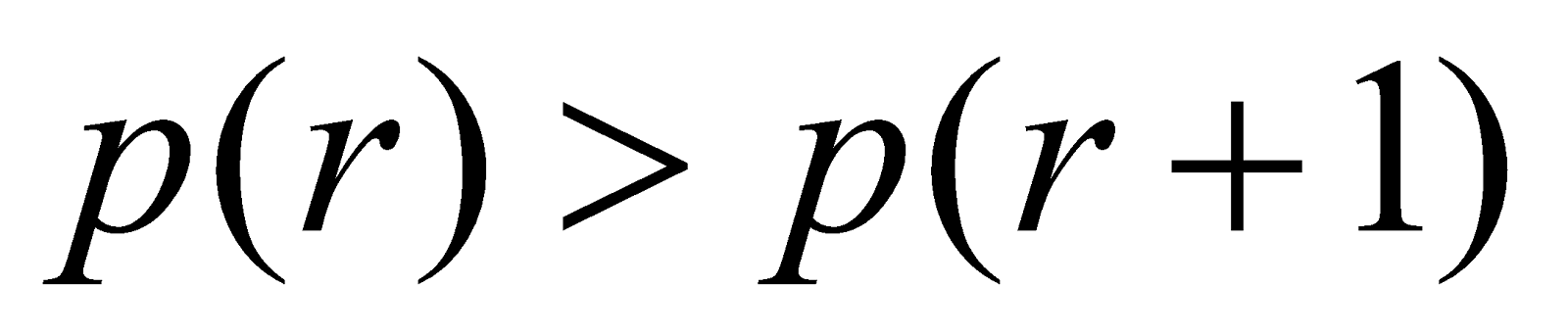
METHOD OF FINDING MODE
Let X, n, p be respectively binomial variate and the two parameters
Case I. If (n + 1)p is a positive integer
Let 
.
.
The binomial distribution will be bimodal, the modal values of X being k and k – 1.
Example :
Find the mode of the binomial distribution for which the parameters are n = 9,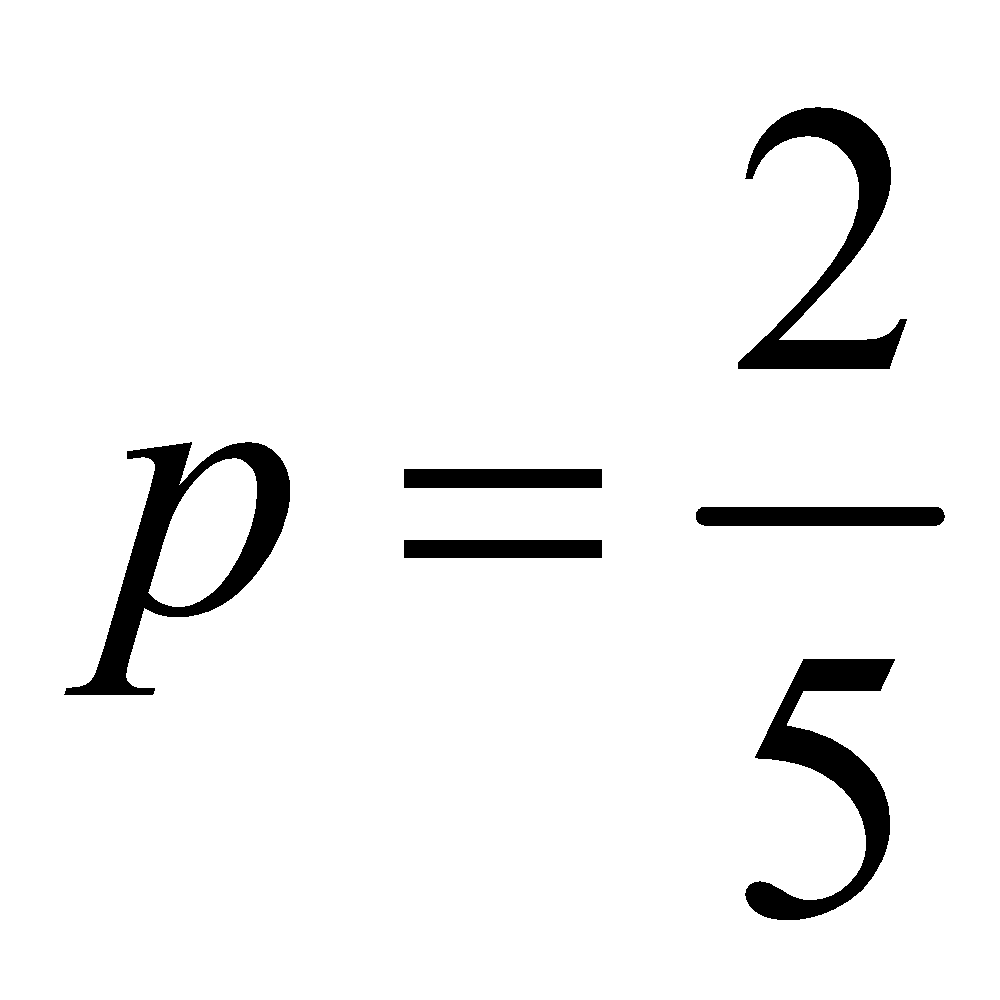 
.
.
Here 
∴ The two modal values of X are 4 and 3
Case II. If (n + 1)p is not an integer
Let (n + 1) p = k + f 0 < f < 1 and 
.
.
The binomial distribution will have unique mode (unimodal), the modal value of X being k.
Example :
Find the mode of the binomial distribution of which the parameters are n = 7 and 
.
.
Here 
; ∴ k = 3
; ∴ k = 3
∴ modal value of X = 3.
Note : If np = integer, the binomial distribution will be unimodal and the mean = mode.
EXPECTED FREQUENCY OF SUCCESSES IN BINOMIAL DISTRIBUTION
Let X be the binomial variate and n, p be the parameters. Then the frequency of X = r successes is given by ; r 
= 0, 1, 2, ...., n
= 0, 1, 2, ...., n
Where N is the number the times the trial is repeated.
MULTINOMIAL DISTRIBUTION
The binomial distribution is generalized as follows : Suppose the sample space of an experiment is partitioned into , say, mutually exclusive events A1, A2 .....As , with respective probabilities p1, p2, ...., ps.
Then in n-repeated trials, the probability that A1 occurs k1 times, A2 occurs k2 times, ... and As occurs ks times, is equal to 
.
.
where k1 + k2 + ..... + ks = n.
The above numbers form the so-called multinomial distribution since they are precisely the terms in the expansion of (p1 + p2 + .... + ps)n
POISSON DISTRIBUTION
Poisson distribution is considered as a limiting case of Binomial distribution when
- the number of trials
- the constant probability of success, in one trial,
Binomial probability function tends to the probability function of Poisson’s distribution and it is given by
; r =0, 1, 2, ..........
where X is the number of successes (i.e., occurrences of the event) and m = np = finite.
IMPORTANT POINTS
- This can be derived from
where np = m and p + q = 1
- Poisson distribution is also a discrete probability distribution.
- As all the probabilities of the Poisson distribution can be obtained by knowing m, we call m as the parameter of the Poisson distribution.
- Total probability =
- Mean for Poisson Distribution
- Variance for Poisson Distribution
Variance 
MODE OF POISSON DISTRIBUTION
The mode of the Poisson distribution is X = r if p(r) is the maximum i.e.,
p(r) > p (r – 1) and p(r) > p (r + 1)
p(r) > p (r – 1) and p(r) > p (r + 1)
METHOD OF FINDING MODE
Case I : If m is a positive integer
In this case Poisson distribution is bimodal and the two modal values of X are m and m – 1.
Case II : When m is not an integer. Let m = k + f, , 0 < f < 1
In this case the Poisson distribution is unimodal (i.e., mode is unique) and the modal value of X is k (i.e the integral part of m).
EXPECTED FREQUENCY OF SUCCESSES IN A POISSON DISTRIBUTION
The frequency of X = r successes is given by
; r = 0, 1, 2, .....
where N is the total observed frequency and m is the parameter, being m = np = finite.
Study Notes for JEE Main/JEE Advanced/BITSAT
