THREE DIMENSIONAL GEOMETRY
THREE DIMENSIONAL CARTESIAN COORDINATE SYSTEM
In the plane geometry or analytical geometry in two dimensions, we know a one-one correspondence between the points in a plane and ordered pairs (x, y) of real numbers through a two dimensional Cartesian coordinate system, by fixing a point O as origin and two mutually perpendicular lines through O as x-axis and y-axis generating the plane. We extend this coordinate system to three dimensions by taking a third line through O perpendicular to both the axes as the z-axis. thus three dimensional Cartesian coordinate system consists of an arbitrary point O in space and three mutually perpendicular lines X'OX, Y'OY, and Z'OZ through O. The point O is called the origin of the coordinate system and the lines X'OX, Y'OY, Z'OZ are called respectively the x-axis, the y-axis, and the z-axis. The positive directions of the axes are indicated by arrows. The plane determined by the x-axis and the y-axis is called the XOY or xy-plane. The other two planes YOZ (or yz-plane) and XOZ (or xz-plane) are defined similarly. These three planes are called the coordinate planes.
Note : The configuration of axes shown in above figure is called a right handed system because a 90° rotation of the positive side of the x-axis into the positive side of the
y-axis will advance a right handed screw along the positive side of the z-axis. If the locations of the x- and y-axis are interchanged, then the system is left-handed.
y-axis will advance a right handed screw along the positive side of the z-axis. If the locations of the x- and y-axis are interchanged, then the system is left-handed.
COORDINATES OF A POINT IN THREE DIMENSIONAL SPACE
Let P be any point in space. Through P draw the three planes parallel to the three coordinate planes (which will automatically be also perpendicular to the corresponding axes, that is, the plane parallel to the yz-plane will be perpendicular to the x-axis, etc.) to meet the axes in A, B and C.
- If OA = x, OB = y, OC = z, then the three numbers x, y, z taken with proper signs are called the coordinates of point P, and written as ordered triplet (x, y, z).
- Thus, the coordinates of a point in space are the distances of the origin from the points of axes in which the planes through that point parallel to the coordinate planes intersect the axes.
Conversely, given three numbers x, y, z, we can find a point whose coordinates are (x, y, z). To do this we proceed as follows:
- Measure OA, OB, OC along the x-axis, the y-axis and the z-axis equal to x, y, z respectively.
- Through A, B, C draw respectively planes parallel to the coordinate planes YOZ, ZOX, XOY intersecting each other at P. Then P is the required point whose coordinates are (x, y, z).
- Thus, there exists a one-one correspondence between the points in space and the ordered triplets of real numbers
(x, y, z). - The coordinate planes divide space into eight regions called, octants. Usually one of them is numbered, and it is called the first and is one in which all the coordinates of every point are positive.
The following table gives the sign in the eight octants :
These are called I, II, III .... VIII octants in that order. The coordinates of a point P may also be taken as the perpendicular distances of the point P from the three rectangular coordinate planes yz, zx and xy respectively.
- Alternatively, the coordinates of any point P may also be taken as the distances from origin of the feet A, B, C respectively of the perpendiculars let fall from the point P to the coordinates axes X'OX, Y'OY and Z'OZ.
- Clearly, the perpendicular distance of P(x, y, z) from the x-axis =
- Similarly, the perpendicular distances of P from the y-axis and z-axis respectively are
and
.
Further, the coordinates of feet of perpendiculars A, B and C upon coordinate axes from P are respectively, (x, 0, 0), (0, y, 0) and (0, 0, z).
DISTANCE BETWEEN TWO POINTS
Let P (x1, y1, z1) and Q (x2, y2, z2) be two given points. The distance between these points is given by
The distance of a point P (x, y, z) from origin O is
SECTION FORMULAE
- The coordinates of any point, which divides the join of points (x1, y1, z1) and (x2, y2, z2) in the ratio m : n internally are
- The coordinates of any point, which divides the join of points (x1, y1, z1) and (x2, y2, z2) in the ratio m : n externally are
- The coordinates of mid point of P and Q are
- Coordinates of any point on the joint of points. P (x1, y1, z1) and Q(x2, y2, z2) are
- Coordinates of the centroid of a triangle formed with vertices P(x1, y1, z1), Q(x2, y2, z2) and R(x3, y3, z3) are
CENTROID OF A TETRAHEDRON
If (x1, y1, z1) (x2 , y2 , z2) (x3 , y3 , z3) and (x4, y4, z4) are the vertices of a tetrahedron, then its centroid G is given by
Example :
Find the coordinates of the points, which trisect AB given that A is (2, 1, –3) and B is (5, –8, 3).
Solution :
The points of trisection divide AB in ratio 1 : 2 and 2 : 1 respectively. Thus the required points are 

or (3, –2, –1) or (4, –5, 1).
DIRECTION COSINES AND DIRECTION RATIOS OF A LINE
Let AB is a given straight line in space.
Let the line OP, parallel to the given line AB, make angles in anti-clockwise direction with positive directions of OX, OY, OZ respectively, then are known as the direction cosines of OP and hence of AB and are generally denoted by the letters l, m, n respectively, i.e. l = cos α, m = cos β, n = cos γ.
The angles are known as the direction angles and satisfy the condition that .
.
IMPORTANT RESULTS
- In the above definition the line OP has its initial point at the origin. If a given line does not have its initial point at the origin, then we can draw a parallel line of the same magnitude having its initial point at the origin.
- The direction cosines completely specify the direction of the line OP but do not say anything about its magnitude.
- Since
makes angles with OX, OY, OZ respectively, therefore, the direction cosines of
are
,
i.e ., or –l, –m, –n. (See figure).
., or –l, –m, –n. (See figure).
- The x-axis makes angles of
with the axes of x, y, z respectively. So, the direction cosines of the x-axis are 1, 0, 0. Similarly the direction cosines of the y-axis and z-axis are respectively 0, 1, 0 and 0, 0, 1.
- If l, m, n are direction cosines of a line OP and (x, y, z) are the coordinates of P, then x = lr, y = mr and z = nr, where r = OP.
- The sum of squares of the direction cosines of a line is unity, that is, l2 + m2 + n2 = 1.
DIRECTION RATIOS OR DIRECTION NUMBERS
If a, b, c be three numbers proportional to the actual direction cosines l, m, n of a line, then the numbers a, b, c are called direction ratios (briefly written as (D.R.)) of the given line.
We have, 
So, 
where the signs should be taken all positive or all negative.
Note : Direction cosines of a line are unique but the direction ratios of a line are not unique. If a, b, c are the direction ratios of a line, then ka, kb, kc are also direction ratios of that line where k is any non-zero real number.
DIRECTION RATIOS OF A LINE JOINING TWO POINTS
Let A (x1, y1, z1) and B (x2, y2, z2) be the two given points.
Then the direction ratios of the line AB are 
Note : While the direction cosines of line AB determined by points A(x1, y1, z1) and B(x2, y2, z2) and directed from A to B are
those of line BA directed from B to A are
In case the given line is undirected, it is immaterial which set of direction cosines are used.
STRAIGHT LINE IN SPACE
Equation of a straight line passing through a fixed point A (x1, y1, z1) and having direction ratios a, b, c is given by
Any point P on this line may be taken as , where is parameter. If a, b, c are replaced by direction cosines l, m, n then λ represents distance of the point P from the fixed point A.
Equation of a straight line joining two fixed points A (x1, y1, z1) and B (x2, y2, z2) is given by
ANGLE BETWEEN TWO INTERSECTING LINES
If l1, m1, n1 and l2, m2, n2 be the direction cosines of two given lines, then the angle θ between them is given by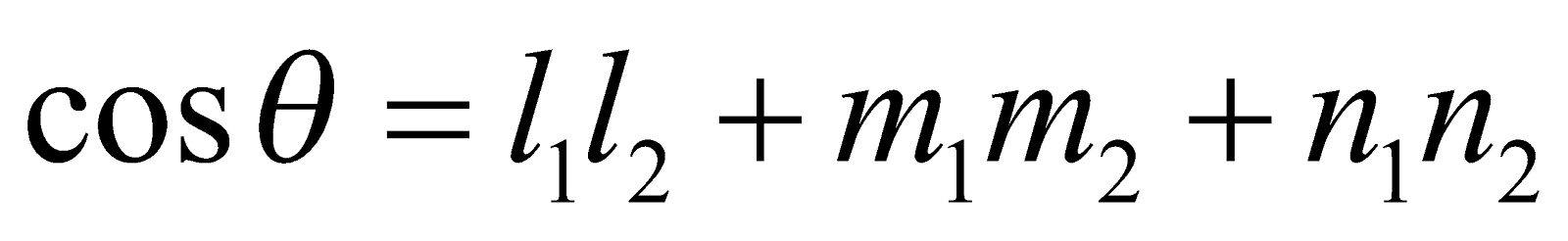
ANGLE IN TERMS OF THE DIRECTION RATIOS OF THE LINE
If the direction cosines of two lines be proportional to a1, b1, c1 and a2, b2, c2 then their actual values are 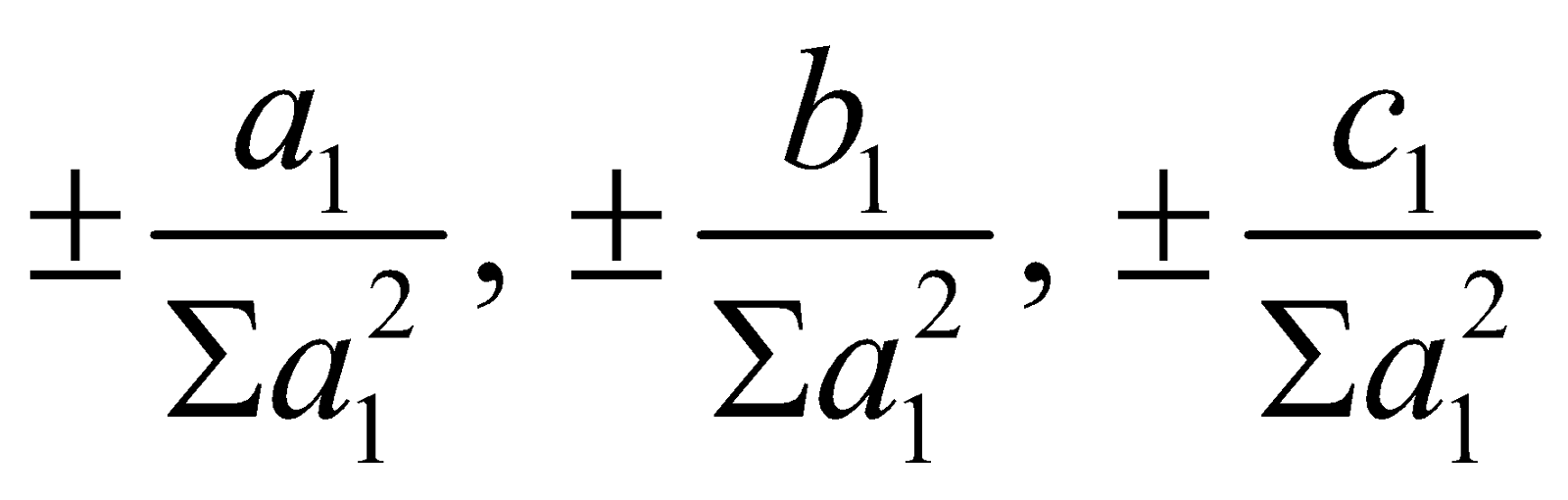 and
and  ,
,
where 
LAGRANGE'S IDENTITY
Lagrange's Identity is very useful result applied for simplifying the denominators of above formula and similar other expressions occurring in other branches of mathematics.
SINE FORM AND TANGENT FORM OF THE ANGLE FORMULA
We have, 
= 

If the direction cosines of two lines be proportional to a1, b1, c1 and a2, b2, c2, then their actual value are
The expression for tan θ is of the same form whether we use direction cosines or direction ratios.
CONDITIONS OF PERPENDICULARITY AND PARALLELISM
- When the given lines are perpendicular to each other, then
so that
.
- When the given lines are parallel to each other, then
so that
. From which we get
.
- If a1, b1, c1 and a2, b2, c2 be the direction ratio of two lines respectively. Then
They are perpendicular, if 
They are parallel, if .
.
PROJECTION OF THE JOIN OF TWO POINTS ON GIVEN LINE
The projection of the join of the points P (x1, y1, z1), Q(x2, y2, z2) on a line AB whose direction cosines are l, m, n is l (x2 – x1) + m(y2 – y1) + n (z2 – z1).
SHORTEST DISTANCE BETWEEN TWO STRAIGHT LINES
- Two straight lines, which are neither intersecting nor parallel are called Skew Lines. Two skew lines are non-coplanar.
- The shortest distance between two skew lines is the length of the common perpendicular to two lines lying between the lines.
Clearly the shortest distance between two intersecting lines is zero.
- Let two non-coplanar (skew) lines be
The shortest distance (S.D.) between the lines is given by
COPLANAR LINES
Two straight lines are coplanar if they are intersecting or parallel.
Thus the two straight lines given above are coplanar if
PLANE
A plane is a surface such that if two points are taken in it, straight line joining them lies wholly in the surface.
GENERAL EQUATION OF THE PLANE
The general equation of the first degree in x, y, z always represents a plane. Hence, the general equation of the plane is ax + by + cz + d = 0.
Note :
- The equation of plane contains only three independent constants, because, the equation may be reduced to px + qy + rz + 1 = 0 by dividing by d, and
etc.
- If the plane passes through origin, d = 0. Hence, the equation reduces to ax + by + cz = 0.
EQUATION OF A PLANE PASSING THROUGH A FIXED POINT
The equation of a plane passing through a given point
(x1, y1, z1) is given by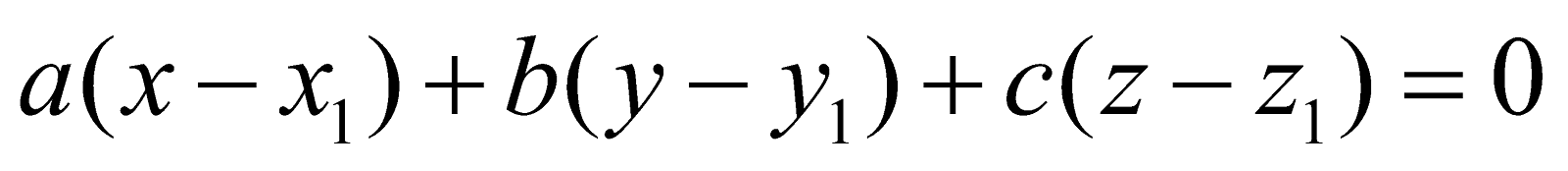
(x1, y1, z1) is given by
Example 1 :
Find the equation of plane through the points P(2, 2, –1), Q(3, 4, 2) and R(7, 0, 6).
Solution :
Any plane passing through P(2, 2, –1) is given by ....(1)
....(1)
It passes through Q(3, 4, 2) and R(7, 0, 6). Thus a + 2b + 3c = 0 and 5a – 2b + 7c = 0.
These give 

Substituting in (1), we get
Example 2 :
Show that the four points (0, –1, –1), (4, 5, 1), (3, 9, 4) and (–4, 4, 4) are coplanar.
Solution :
Any plane through (0, –1, –1) is ax + b(y + 1) + c (z + 1) = 0 ...(1)
It will pass through (4, 5, 1) and (3, 9, 4) if 4a + 6b + 2c = 0 ...(2)
and 3a + 10b + 5c = 0 ...(3)
These equations give , or
, or 
The plane through (0, –1, –1), (4, 5, 1), (3, 9, 4) is 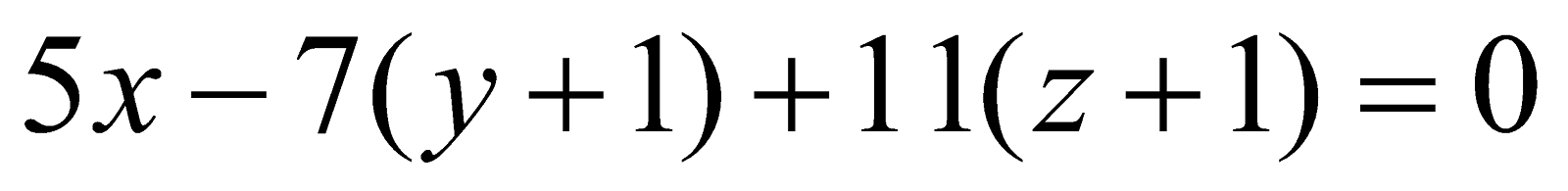 or
or .
.
The point (–4, 4, 4) satisfies the equation and therefore lies on the plane represented by it. Hence, all the four points are coplanar.
NORMAL FORM OF THE EQUATION OF PLANE
- The equation of a plane, which is at a distance p from origin and the direction cosines of the normal from the origin to the plane are l, m, n is given by lx + my + nz = p
- The coordinates of foot of perpendicular N from the origin on the plane are (lp, mp, np).
TO REDUCE THE GENERAL EQUATION TO THE NORMAL FORM
Let the general equation of a plane be
ax + by + cz + d = 0 ....(1)
Let the normal form of the same plane be
lx + my + nz – p = 0 ....(2)
(1) and (2) are identical if
Thus  and as p is always positive, we shall take positive or negative sign with the radical according as d is negative or positive.
and as p is always positive, we shall take positive or negative sign with the radical according as d is negative or positive.
If d is positive, then
If d is negative, we have only to change the signs of all these. Hence, the normal form of ax + by + cz + d = 0 is
INTERCEPT FORM OF THE EQUATION OF THE PLANE
Equation of a plane which cuts off intercepts a, b and c respectively on the axes of x, y and z is
TO REDUCE THE GENERAL EQUATION TO THE INTERCEPT FORM
The general equation of the plane is ax + by + cz + d = 0
This can be written as ax + by + cz = –d
or  or
or , which is the required intercept form.
, which is the required intercept form.
SOME ELEMENTARY EQUATIONS REPRESENTING PLANES
EQUATIONS OF COORDINATE PLANES
If we consider any point on xy-plane, it will have coordinates (x, y, 0). That is for any point on xy plane, z = 0. Hence the equation of xy plane is z = 0.
Similarly, the equation of yz plane is x = 0 and the equation of zx plane is y = 0.
EQUATION OF PLANES PARALLEL TO COORDINATE PLANES
Consider a plane at a distance 'a' from the yz plane and parallel to it. Clearly, for any point on this plane, the x-coordinate will remain a. Hence, the equation of this plane is x = a.
Similarly the equation of a plane parallel to xz plane and at distance b from it is y = b.
The equation of a plane parallel to xy plane and at distance c from it is z = c.
Note that the equation x = a represents a point on real number line (x-axis), i.e. in one dimension. Further, x = a represents a straight line parallel to y-axis in plane geometry or in two dimensions. Hence the locus depends on the number of dimensions also.
TRACE
The trace on a coordinate plane of a given plane π is the line of intersection of the plane π and the coordinate plane.
If the plane π has the equation ax + by + cz + d = 0, then the equations or the trace are given by
Note : The trace on xy-plane can never be written as ax + by + d = 0, obtained by substituting z = 0, as it does not represent a straight line in 3-D but a plane. Thus z = 0 must be written with the given equation. We may write the equation of trace on xy plane as ax + by + d = 0, z = 0
The curve of intersection of two planes is a straight line, provided the planes are not parallel, but its equation cannot be given uniquely. The straight line which is intersection of planes π1 = 0 and π2 = 0 is simply written as a set of simultaneous equations π1 = 0, π2 = 0
Example :
For the plane 2x + 3y + 6z – 18 = 0, find the intercepts on the coordinate axes. Also find the equations of its trace on the xy-plane.
Solution :
2x + 3y + 6z – 18 = 0 .....(1)
To get the intercept on the x-axis we put y = 0, z = 0.
In a similar way by putting x = 0, z = 0, the y intercept will be found to be 6. By putting x = 0, y = 0, the z intercept will be found to be 3.
The equations of the trace in the xy-plane are 2x + 3y + 6z – 18 = 0, z = 0, or more simple 2x + 3y = 18 and z = 0.
ANGLE BETWEEN TWO PLANES
The angle between two planes is defined as the angle between the normals to them from any point.
Thus the angle between the two planes
is equal to the angle between the normals with direction cosines
If θ is the angle between the normals, then
The angle between two planes is called the DIHEDRAL ANGLE.
PARALLELISM AND PERPENDICULARITY OF TWO PLANES
Two planes are parallel or perpendicular according as the normals to them are parallel or perpendicular.
Hence, the planes  and
and  are parallel if
are parallel if , perpendicular, if
, perpendicular, if 
Note : The equation of plane parallel to a given plane ax + by + cz + d = 0 is given by ax + by + cz + k = 0, where k may be determined from given conditions.
ANGLE BETWEEN A LINE AND A PLANE
The angle between a line and plane is defined as the complement of the angle between the line and normal to the plane.
Example :
Find the angle between the plane x + 2y – 3z + 4 = 0 and the line whose direction cosines are  .
.
Solution :
The direction ratios of the normal are 1, 2, –3.
The d.c.'s of the normal are 
The d.c.'s of the line are .
.
Let θ be the angle between the normal and the given line. Then
= 
So, the angle between the plane and line = 90° – θ
RELATIVE POSITIONS OF TWO POINTS WITH RESPECT TO A PLANE
Two points A (x1, y1, z1) and B (x2, y2, z2) lie on the same or different sides of the plane
ax + by + cz + d = 0, according as the expressions ax1 + by1 + cz1 + d and ax2 + by2 + cz2 + d are of the same or different signs.
or according as  is positive or negative.
is positive or negative.
DISTANCE OF A POINT FROM A PLANE
Let the plane in the general from be ax + by + cz + d = 0 The distance of the point P(x1, y1, z1) from the plane is equal to 
If the plane is given in normal form lx + my + nz = p. Then the distance of the point P (x1, y1, z1) from the plane is 
Example :
The distance of the point P(2, 1, –1) from the plane x – 2y + 4z = 9 is
DISTANCE BETWEEN TWO PARALLEL PLANES
If ax + by + cz + d1 = 0 and ax + by + cz + d2 = 0 be equations of two parallel planes. Then the distance between them is .
.
BISECTORS OF ANGLES BETWEEN TWO PLANES
To find the equations of the bisector planes of the angles between the planes
The bisector planes of the angles between two intersecting planes are the loci of a point (x, y, z) such that the perpendicular distances from this point to the given planes are equal (in magnitude).
Hence, the equations of the bisector planes are
One of these planes will bisect the acute angle and the other the obtuse angle between the given planes.
The bisector of the acute angle makes with either of the planes an angle which is less than 45° and the bisector of the obtuse angle makes with either of them an angle which is greater than 45°. This gives a test for determining which of the two bisector planes bisects the acute angle and which bisects the obtuse angle.
Example :
Find the equations of the planes which bisect the dihedral angle between the planes and , and specify the one which bisects the acute angle.
Solution :
The given planes are
The equations of the bisector planes are given by
On simplification we get  ....(3)
....(3)
and ....(4)
....(4)
and
which are the required bisector planes.
Let us now find the angle between (1) and (3), say. The direction cosines of the normals to (1) and (3) are and
and 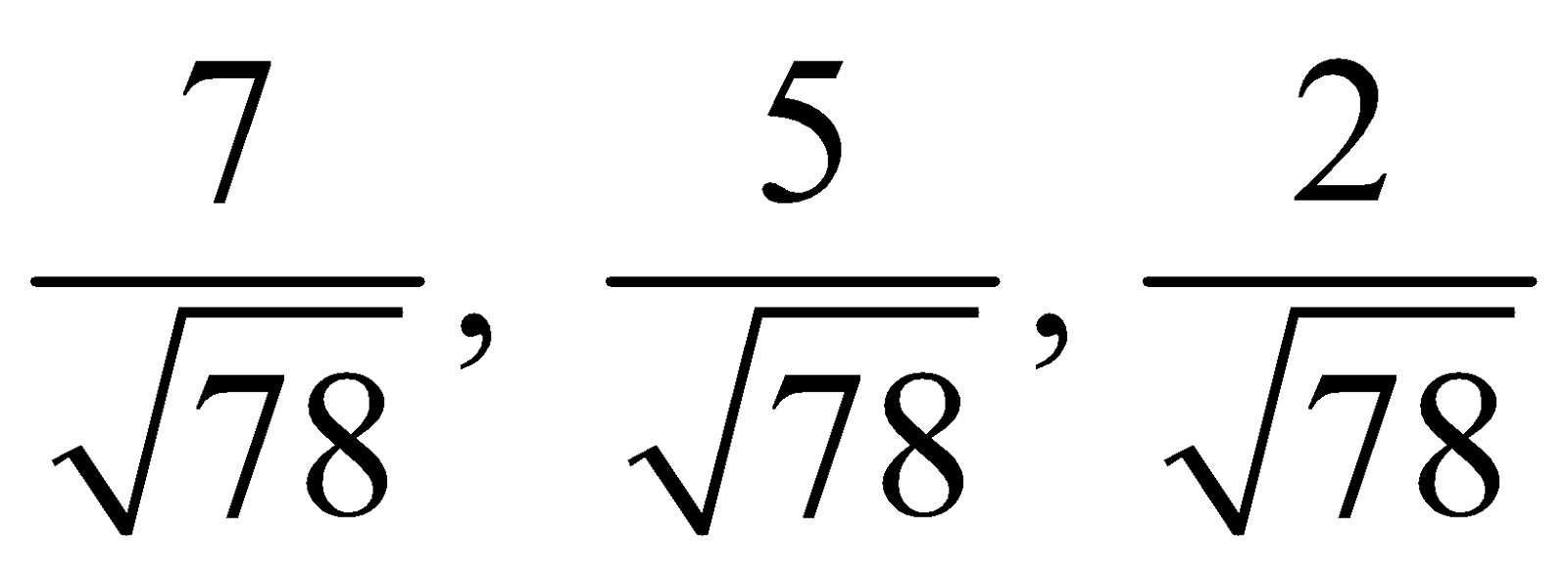 .
.
If θ is the angle between them, then
∴ (3) bisects the obtuse angle. Hence the other bisector plane, namely is the bisector of acute angle.
is the bisector of acute angle.
EQUATIONS OF SOME PARTICULAR PLANES
- The equation ax + by + cz + k = 0 represents a system of planes parallel to the plane ax + by + cz + d = 0, k being a parameter.
- The equation ax + by + cz + k = 0 represents a system of planes perpendicular to the line with direction ratios a, b, c; k being a parameter.
- The equation (a1x + b1y + c1z + d1) + k (a2x + b2y + c2z + d2) = 0 represents a system of planes passing through the line of intersection of the planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0; k being a parameter.
- If ax + by +cz + d = 0 is perpendicular to the plane x = 0, then
a × 1 + b × 0 + c × 0 = 0, i.e. a = 0
Therefore, by + cz + d = 0 is perpendicular to the plane x = 0.
Similarly, ax + cz + d = 0 is perpendicular to the plane
y = 0; and ax + by + d = 0 is perpendicular to the plane z = 0.
y = 0; and ax + by + d = 0 is perpendicular to the plane z = 0.
- Any plane perpendicular to the axis of x is evidently parallel to the yz-plane and its equation is x = a. Similarly, the equations of the planes perpendicular to the y-axis and the z-axis and y = b and z = c respectively.
- Equations of the planes parallel to the coordinate axes are, by + cz = d, ax + cz = d, ax + by = d parallel to the x-axis, the y-axis, the z-axis respectively.
CONDITIONS FOR A LINE TO BE PARALLEL ON OR BE PERPENDICULAR TO A GIVEN PLANE
Let the given plane be ax + by + cz + d = 0.
Let the direction cosines of the line be l, m, n. If the line to be parallel the plane, then it is at right angles to the normal to the plane. Therefore al + bm + cn = 0.
If the line is perpendicular to the plane, then it is parallel to the normal to the plane. Therefore  .
.
EQUATIONS OF PLANES WITH GIVEN CONDITIONS
- Equation of a plane passing through the point A(x1, y1, z1) and parallel to two given lines with direction ratios a1, b1, c1 and a2, b2, c2 is
.
- Equation of plane through two points A (x1, y1, z1) and B (x2, y2, z2) and parallel to a line with direction ratios a, b, c is
.
- The equation of a plane passing through three points A (x1, y1, z1), B (x2, y2, z2) and C(x3, y3, z3) is
- Four points A (x1, y1, z1), B (x2, y2, z2), C(x3, y3, z3) and D (x4, y4, z4) are coplanar if and only if
- Equation of the plane containing two coplanar lines
and
is







