Linear Inequalities | Mathematics Notes for IITJEE Main

LINEAR INEQUALITIES

INTERVAL NOTATION IN REAL NUMBERS

Let a and b be two given numbers such that a < b. The set of numbers x, lying between these numbers a and b may be represented in a number of ways as following :

CLOSED INTERVAL

The set of numbers x such that a ≤ x ≤ b is a closed Interval, denoted by [a, b], hence

Thus [a, b] contains all real numbers between the numbers a and b including the numbers a and b too.

OPEN INTERVAL

The set of numbers x, such that a < x < b   is called an open Interval, denoted by (a, b), hence

Thus (a, b) contains all numbers between the numbers a and b however excluding a and b.

SEMI-OPEN OR SEMI-CLOSED INTERVAL

Semi intervals may be defined as follows:

, includes b but excludes a

, excludes b but includes a

REMARKS

• The number 'b – a' is referred to as the length of any of the above intervals.
• Let a be a real number then the set of all the real numbers x > a are denoted by and is denoted by
• Similarly if b is a real number, then x < b is equivalent to and is equivalent to

MODULUS OF A REAL NUMBERS

Let x be a real number then it may be a positive number, a negative number or zero. By modulus of x (denoted by , read as "mod x") we mean the absolute value of the number x, i.e., its magnitude only without any consideration to sign. We define

  

Example :

| 3 |    = 3, as 3 > 0,

| 0 |    = 0

| -2 | =  –(–2) = 2, as –2 < 0

Hence the above definition makes always nonnegative, whether x is positive or negative. We may give following alternate representations

| x |  = max {x, -x}

| x |  

PROPERTIES OF MODULUS

Let x and y be real numbers then

1. | x |, i.e., modulus of a real number is always non-negative
2. | x | > x,
3. 
4. 

In inequalities 3 and 4 equality holds if and only if
x.y > 0.

5. 
6. 
7. If then where 'a' is a nonnegative real number
8. If | x | < a, then – a < x < a, where a is a  positive real number.
9. If | x | > a, then x < –a or x > a, where a is a non-negative real number.

MODULUS OF A FUNCTION

Let f(x) is a function of real number x, then

              

Example :

1. 

      

2. 

3. 

Students have a common tendency of applying the conditions and on every situation. Note that these conditions were applied basically to define absolute value of the number x. Hence in a problem of the type containing , one must apply conditions and (see above examples). See the illustrative examples for better understanding.

GENERAL THEORY OF POLYNOMIAL EQUATIONS

Consider the equation

.

The above equation (1) is a polynomial equation of nth degree. It has exactly n roots. Let the roots of equation (1) be then

and

                  

                                                    

For example :

If α, β, γ be the roots of cubic equation  ax3 + bx2 + cx + d = 0.

Then ; ;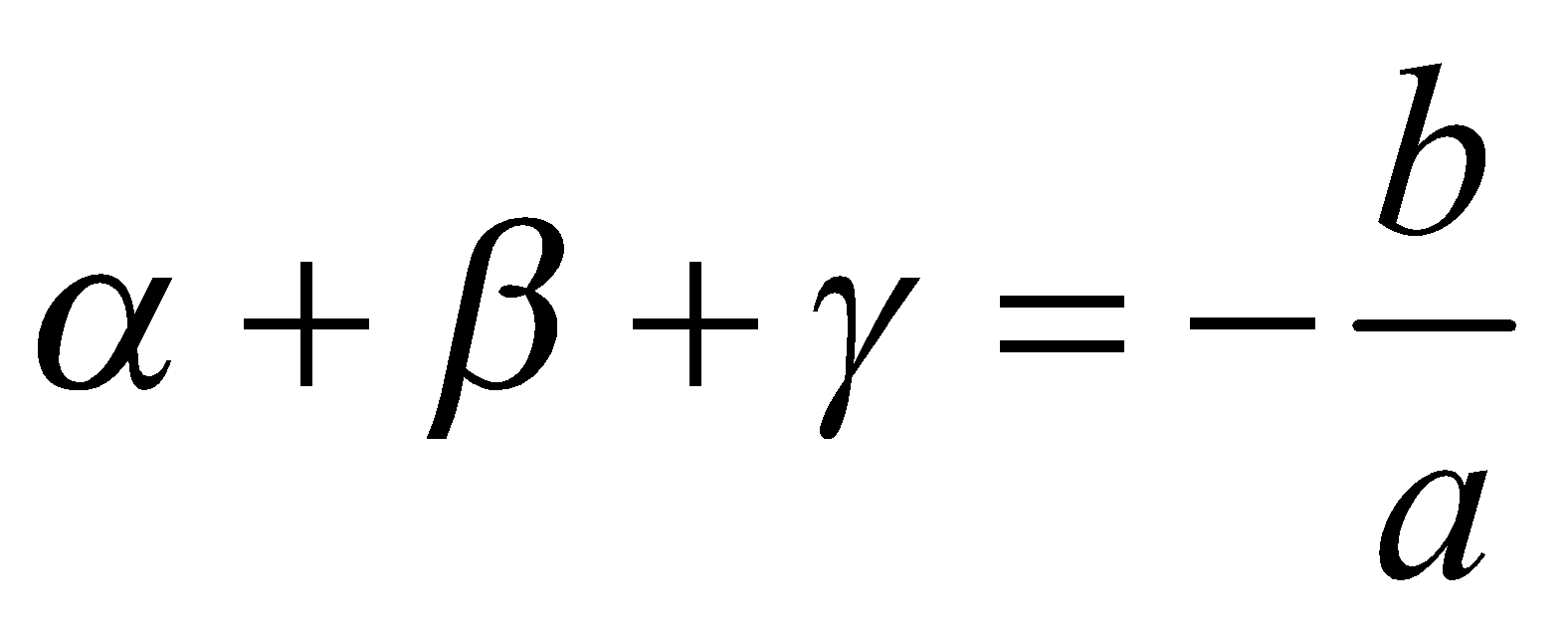

If be the roots of bi-quadratic equation

ax4 + bx3 + cx2 + dx + e = 0

Then ;

;

Note : The general quadratic expression ax2 + 2hxy + by2 + 2gx + 2fy + c in x and y may be resolved into two linear rational factors if abc + 2fgh – af2 – bg2 –ch2 = 0

or

SOLVING INEQUALITIES USING METHOD OF INTERVALS (WAVY CURVE METHOD)

Consider a polynomial expression f(x) of n degree, expressed in terms of linear factors :

Let

To determine the sign of f(x), we may draw the following curve

+ and – signs represent the sign scheme for f(x) in various intervals. We draw the above curve from above the real line right to left alternatively changing the curve at points

RATIONAL INEQUALITIES

Consider the inequality

The above inequality is solved by multiplying numerator and denominator by g(x),

We get and

The above inequality can now be solved by using method of intervals.

LOGARITHMIC EQUATIONS AND INEQUALITIES

If ab = c, then b is said to be the logarithm of c to the base a and we write. Where,

LAWS OF LOGARITHMS

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 

SOLVING LOGARITHMIC EQUATION

1. If where
2. If
3. If

SOLVING LOGARITHMIC INEQUALITIES

1. If if 0 < a < 1
2. If if a > 1 and x > y if 0 < a < 1

EQUATION AND INEQUALITIES CONTAINING GREATEST INTEGER FUNCTION [X]

Let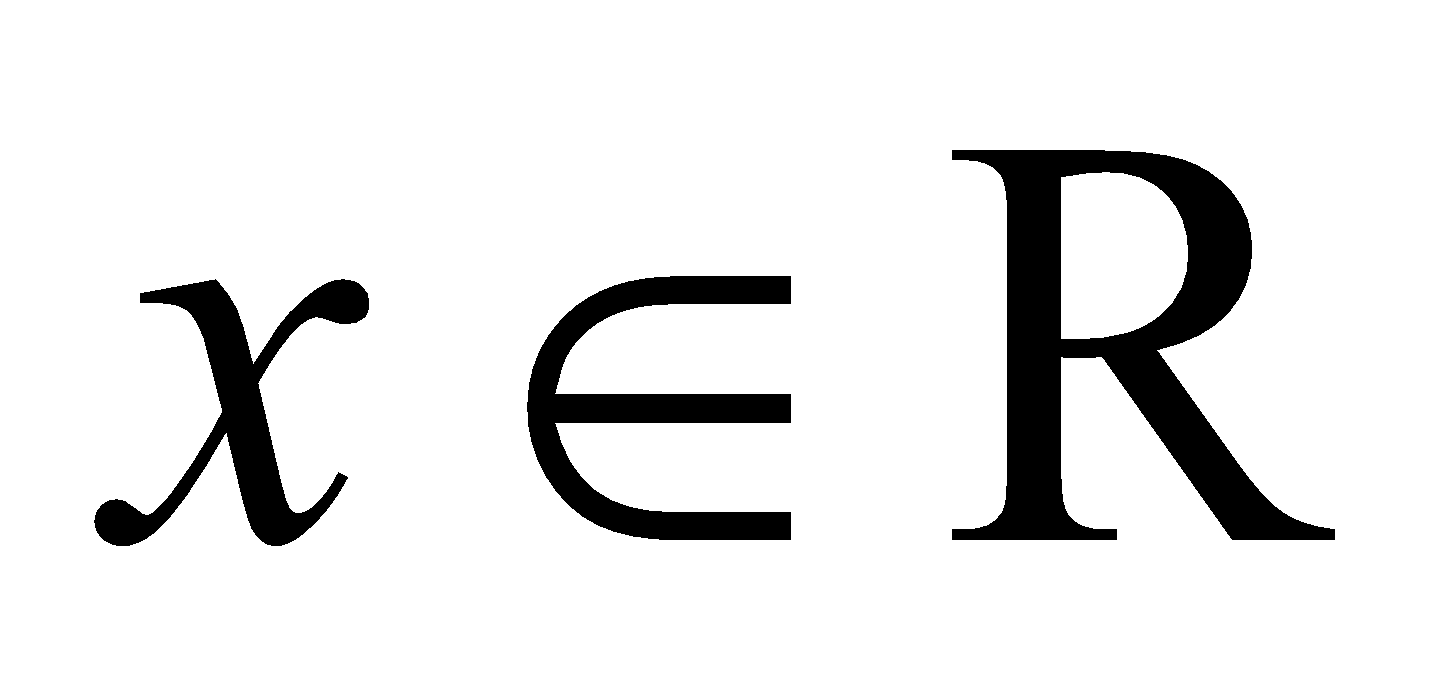. x can always be expressed as a sum of an integer and a pure fraction. Thus,

x = I + f, where I is an integer and
I is called integral part of x and f is fractional part of x.

We often denote I by [x] and f by {x}

∴     [x] = the integral part of x

           = the greatest integer less than or equal to x

and {x} = the fractional part of x 

PROPERTIES OF [X]

1. x = [x] + {x}
2.  
3. 
4. 
5. 
6. 
7. 
8. For any x  ∈ R and n ∈ N

 

Example:

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT