COMPLEX NUMBERS

INTRODUCTION

Consider a simple quadratic equation x2 + 4 = 0. Clearly there is no solution of this equation in the set of real numbers. To permit the solution of such equations the set of complex numbers is introduced.
The solutions of the above equation are given by x2 = –4
Swiss Mathematician Euler introduced the symbol i (iota) for positive square root of – 1, i.e., i = .

The square root of a negative number is called an imaginary number.

Now for any two real numbers x and y, we can form a new number x + iy. This number x + iy is called a complex number. The set C of complex numbers is therefore defined by C = {x + iy | xR, yR}

The extension of concept of numbers from real numbers to complex numbers enabled us to solve any polynomial equation.

A complex number is denoted by a single letter such as z, ω etc. Given a complex number z = x + iy, x is called its Real part and y its Imaginary Part and we denote

x = Re(z) and y = Im (z)

If y = 0, then z = x is a purely real number.
If x = 0, then z = iy is a purely imaginary number.
The complex number 0 = 0 + i0 is both purely real as well as purely imaginary.

Two complex numbers z1 = x1 + iy1 and z2 = x2 + iy2 are said to be equal if and only if x1 = x2 and y1 = y2.

AXIOMATIC APPROACH TOWARDS THE COMPLEX NUMBER SYSTEM

A complex number is defined as an ordered pair (x, y) of real numbers x and y.
Thus, C = {(x, y) | x

R, y

If z = (x, y) then x = Re(z) and y = Im (z), z = (x, y) is equivalent to z = x + iy.

Thus, i is equivalent to (0, 1) and

= (x, –y)

IMPORTANT RESULTS TO BE MEMORISED ABOUT i

i (greek letter iota) represents positive square root of –1, so, . It is called imaginary unit. We have

Thus for any integer k,

i4k = 1, i4k+1 = i, i4k+2 = –1, i4k+3 = –i.

That is if power of i is m, , then divide m by 4 and find the remainder.

If the remainder is zero, then im = 1

If the remainder is one, then im = i

If the remainder is two, then im = –1

If the remainder is three, then im = –i

The sum of four consecutive powers of i is zero, for example, i12 + i13 + i14 + i15 = 0
For any two real numbers a and b, is true only if at least one number is non negative or zero. If both a and b are negative then

In fact if a > 0 and b > 0 then

OPERATIONS ON COMPLEX NUMBERS

Suppose that z1 = (x1, y1) and z2 = (x2, y2) be two complex numbers, that is, z1 = x1 + iy1 and z2 = x2 + iy2

Equality : z1 = z2, if x1 = x2 and y1 = y2
Addition : z1 + z2 = (x1 + x2, y1 + y2) or equivalently z1 + z2 = (x1 + x2) + i (y1 + y2)
Subtraction : z1 – z2 = (x1 – x2, y1 – y2) or equivalently z1 – z2 = (x1 – x2) + i (y1 – y2)
Multiplication : z1z2 = (x1x2 – y1y2, x1y2 + x2y1) or equivalently z1z2 = (x1x2 – y1y2) + i (x1y2 + x2y1)
Division : If z2 0 then

or equivalently

Multiplication by a real number : If z = (x, y) and m R then mz = (mx, my) or equivalently if z = x + iy then mz = mx + imy

ALGEBRA OF OPERATIONS

If z1, z2 and z3 belong to set C of complex numbers, then following properties hold.

Closure Property : z1 z2; z1z2 and , z2 0 all also belong to C.
Commutative Property : z1 + z2 = z2 + z1 and z1z2 = z2z1
Associative Property : z1 + (z2 + z3) = (z1 + z2) + z3 and z1 (z2z3) = (z1z2)z3
Cancellation Property : z1 + z3 = z2 + z3 z1 = z2 and z1z3 = z2z3 z3 = 0 or z1 = z2
Distributive Property : z1 (z2 + z3) = z1z2 + z1z3
Existence of Identity : 0 = (0, 0) is additive identity, i.e. 0 + z = z + 0 = zz ∈ C

1 = (1, 0) is multiplicative identity, i.e. 1(z) = (z)1 = z

z ∈ C

Existence of Inverse : For every complex number z = (x, y), we may get a unique number–z = (–x, –y) such that z + (–z) = (–z) + z = 0. (–z) is Additive Inverse.

For every complex number z = (x, y),

we may get a unique number z–1 or

such that

is multiplicative inverse.

Note : A set with two operations on it satisfying all above properties is called a Field.

The order relations 'greater than' and 'less than' are not defined for non real complex numbers. The inequalities like –2i < 0; 1 + 2i > 1; i – 1< i are meaningless.

THE MODULUS AND THE CONJUGATE OF A COMPLEX NUMBER

Let z = x + iy be a complex number. Then the modulus (absolute value) of z, denoted by | z | is defined as follows :

Clearly, modulus of a complex number is a real number. Again let z = x + iy be a complex number. Then the complex number x – iy is called the conjugate of z and is denoted by

or z*.

Thus, we have Re (

) = Re (z) and Im (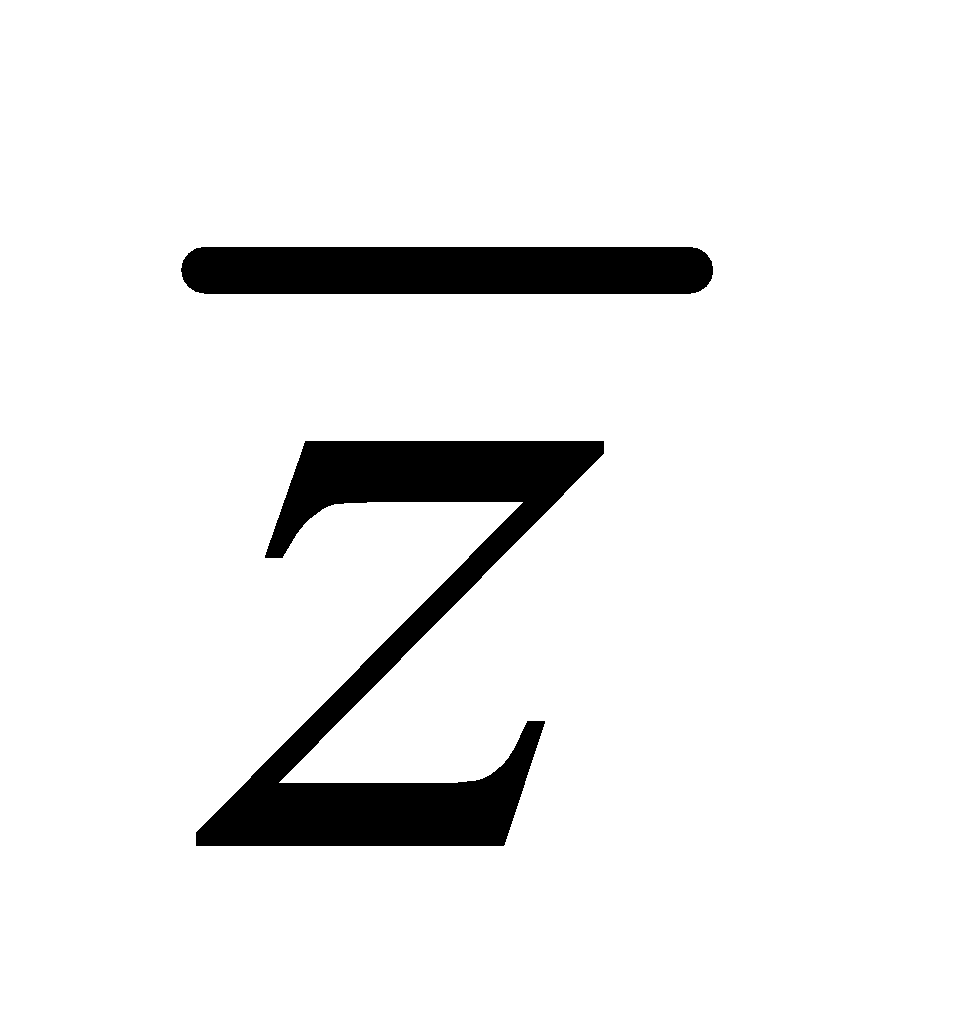

) = – Im (z).

Note :

The additive inverse of ‘z’ is ‘– x – iy’ and conjugate of ‘z’ is ‘x – iy’.
The multiplicative inverse of a non-zero complex number ‘z’ can be given by

IMPORTANT RESULTS TO BE MEMORISED ABOUT CONJUGATE

,
, which is a purely real number
, which is a purely imaginary number.
if and only if z is purely real.
if and only if z is purely imaginary.
If f(z) is a polynomial in a complex variable z, then [where means the complex coefficients are replaced by their conjugate is]
If then

where ai, bi, ci (i = 1, 2, 3) are complex numbers.

GRAPHICAL REPRESENTATION OF COMPLEX NUMBERS

Every complex number x+iy can be represented geometrically as a unique point P (x,y) in the xoy plane with x-coordinate representing its real part and y-coordinate representing its imaginary part.
The Point (x, 0) on the x-axis represents the purely real number x. As such x-axis is called the real axis. Similarly, the point (0, y) on the y-axis represents purely imaginary number iy. Therefore, y-axis is called the imaginary axis.
The plane having a complex number assigned to each of its points, is called the complex plane or Argand plane or Gaussian plane. This representation of complex numbers as points in the plane is known as Argand diagram.
The distance from the origin to the point P(x, y) is defined as the MODULUS (or absolute value) of the complex number z = x + iy, denoted by | z |, thus | z | =
The conjugate of complex number z is represented by the point Q, which is the mirror image of P on the x–axis.

IMPORTANT RESULTS ABOUT MODULUS

, .
(majority of the complex equations are solved using this property)
,
, is a unimodular complex number ().
where a, b ∈ R
If then is purely imaginary.

POLAR FORM (OR TRIGONOMETRIC FORM) OF COMPLEX NUMBERS

Let P represents the nonzero complex number z = x+iy. Let the directed line segment OP be of length r and makes an angle θ with the positive direction of the x–axis (θ in radians)

The point P is uniquely determined by the ordered pair of real numbers (r, θ) called the polar coordinates of the point P. Clearly,

x = r cos θ, y = r sin θ,

, tanθ =

Thus z=r(cosθ + isin θ) is the polar form of z. r is the modulus of the number z and θ is called the ARGUMENT (or AMPLITUDE) of the number z, denoted by arg (z) or amp (z) Hence.

and

z = r(cosθ + i sinθ) is also written as r cis(θ)

Note that θ is not defined uniquely, In fact θ is the solution of simultaneous equations

and

If z = 1 + i,

Polar form of

Clearly the possible arguments of the number z=1+i are the following angles :

Any two arguments of a complex number differ by a number which is a multiple of 2 π.

The unique value of θ, such that

is called the principal value of the Argument.

WORKING RULE FOR FINDING PRINCIPAL ARGUMENT

Let z = x + iy has image P on the argand plane and

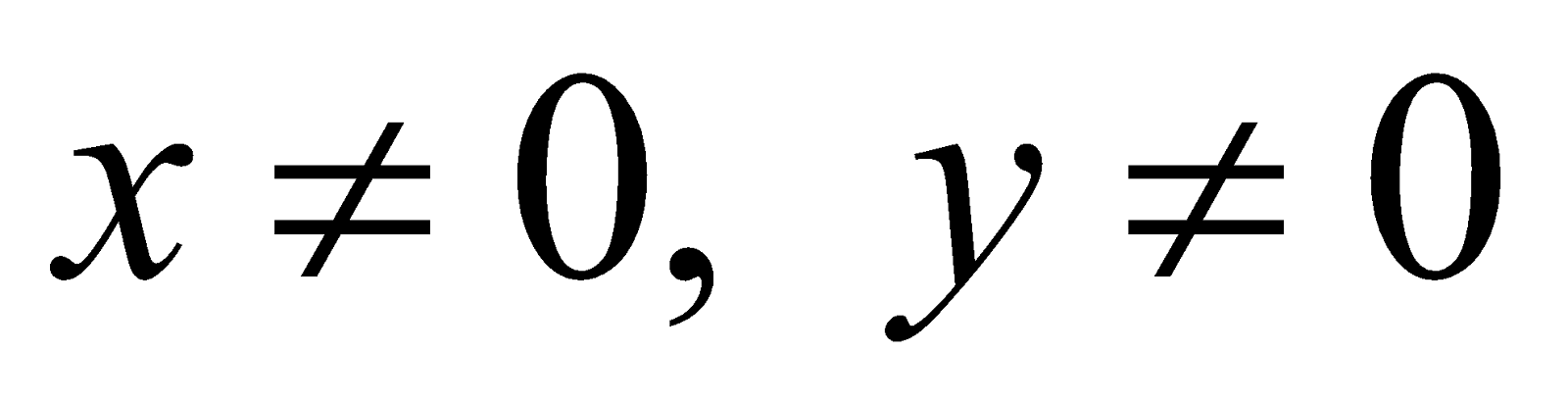
Following cases may arise

Case I : If x > 0, y > 0, then the point P lies in the first quadrant and then

For example, if

, then arg(z) =

Case II : If x < 0, y > 0, then the point P lies in the second quadrant and then

For example, if

, then

Case III : If x < 0, y < 0 then the point P lies in the third quadrant and then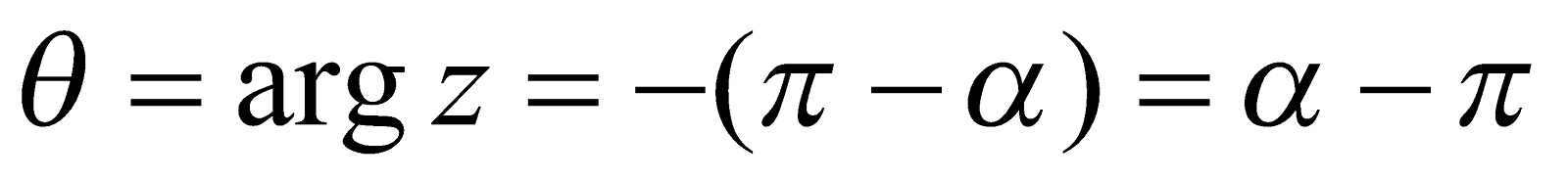

For example, if

, then

Case IV : If x > 0, y < 0 then the point P lies in the fourth quadrant and then

For example, if

then

so,

Case V : If y = 0, then z is purely real and P lies on real axis, and z = x,

so arg (z) = 0 if x > 0; arg (z) = π if x < 0

For example arg(3) = 0 and

Case VI : If x = 0, then z = iy is a purely imaginary number and P lies on imaginary axis

So, arg (z) =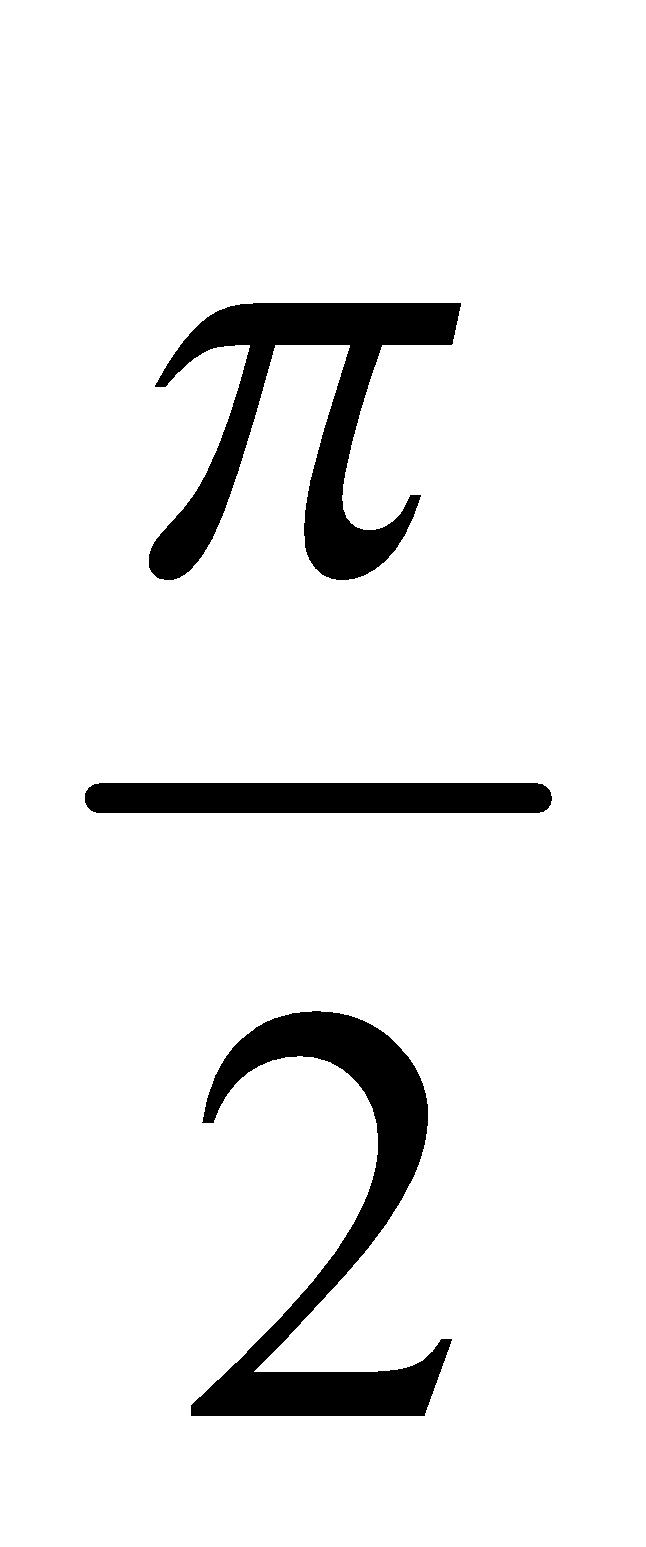

if y > 0 and arg (z) =

if y < 0

For example,

and

IMPORTANT RESULTS ABOUT ARGUMENT

Where k = 0, –1 or 1 would be taken so that the value comes out into the principal value region

If the ,

EULER'S NOTATION

It can be shown that

∴

Also

Again,

LOGARITHM OF A COMPLEX NUMBER

Let

Then

So,

As such the argument of a complex number is not unique, the log of a complex number cannot be unique. In general,

For example,

So,

is one of the values of log (i)

Also,

[Taking principal value only]

DE MOIVRE THEOREM

These are two statements of De Moivre Theorem

(cosθ+i sinθ)n = cos nθ + i sin nθ,
If then cos nθ+i sinnθ is one of the values of (cosθ+ i sinθ)n

IMPORTANT RESULTS

Take care that in fact

ROOTS OF A COMPLEX NUMBER

and n is a positive integer, then

k = 0, 1, 2, ......, n – 1

Putting k = 0, 1, 2, ....., n – 1, we get n values which represent nth roots of complex number z

PROPERTIES

These n roots always form a G. P. with common ratio ei 2π/n
Their images on argand diagram lie on a circle of radius and centre origin.
The points representing these roots from the vertices of a regular polygon of n sides

CUBE ROOTS OF UNITY

, k = 0, 1, 2

So, three cube roots of unity are 1,

and

or 1,

and

So, we denote the non-real roots by ω and ω2 we write mostly

and

ALGEBRAIC METHOD

Let z = (1)1/3

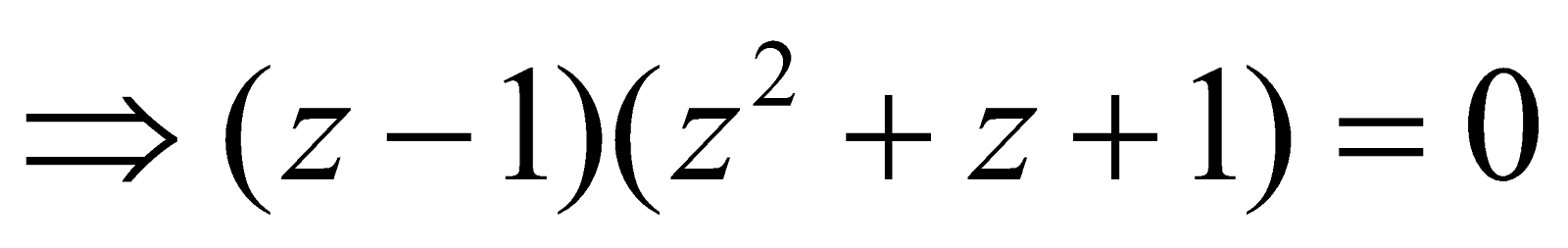, which gives the roots of z as z = 1, the real root and

,the non-real roots , i.e., ω and ω2. Clearly, we can always write

IMPORTANT CHARACTERISTICS OF ω

and , so
and or
For any positive integer k, and
For any real a, b, c;
The cube roots of unity lie on a unit circle and divide the circumference into three equal parts
The points represented by cube roots of unity form the vertices of an equilateral triangle.

SOME USEFUL IDENTITIES

x2 + xy + y2 = (x – yω) (x – yω2), in particular,

x2 + x + 1 = (x – ω) (x – ω2)

x2 – xy + y2 = (x + yω) (x + yω2), in particular,

x2 – x + 1 = (x + ω) (x + ω2)

x2 + y2 + z2 – xy – xz – yz = (x + yω + zω2) (x + yω2 + zω)

nTH ROOTS OF UNITY

Since

, therefore

; k = 0, 1, 2, ........, (n – 1)

; k = 0, 1, 2, ...., (n – 1)

SQUARE ROOTS OF A COMPLEX NUMBER

Let z = x + iy and let the square root of z be the complex number a + ib. Then

Equating real and imaginary part, we get

…(1)

and y = 2ab …(2)

Now,

…(3)

Solving the equations (1) and (3), we get

;

From (2), we can determine the sign of ab. If ab > 0, then a and b will have same sign. Thus

If ab < 0, then

Thus, square roots of z = a + ib are :

for b > 0

and

for b < 0

For example :

Square root of i is , as x = 0, y = 1 > 0 and | i | = 1
Square root of -i is , as x = 0, y = -1 < 0 and | i | = 1
Square root of -3 + 4i is ,
or , As x = –3 and y = 4 > 0.
Square root of is or ; As

GEOMETRY OF A COMPLEX NUMBER

As in vectors, we represent a point by the position vector of the point with respect to origin O. Similarly the point P can be represented by a complex number z, such that length OP= |z| and

. The point P is called the IMAGE of the complex number z and z is said to be AFFIX or complex coordinate of the point P.

DISTANCE BETWEEN TWO POINTS

If two points P and Q have affices z1and z2 respectively then

Affix of Q – Affix of P.

SECTION FORMULA

If a point R (z) divides the join of two points P (z1) and Q (z2) in ratio m : n, then

(internally) and

(externally)

Midpoint of PQ is given by

ANGLE BETWEEN TWO LINES (CONCEPT OF ROTATION)

Consider three points P(z1), Q(z2) and R(z3)

Then angle between PQ an PR (counter clockwise)

If P(z1), Q(z2) and R(z3) be collinear Points, then θ = 0 or π,

i.e.

(A complex number z is purely real if

)

If PR is perpendicular to PQ. Then

is purely imaginary

That is,

(A Complex number z is purely imaginary if z = -

)

Consider Four Points P, Q, R and S with affices respectively and z4. As in (i) the angle between SR and QP.

If SR and QP be perpendicular,

Then

is purely imaginary.

or alternatively

Multiplying a complex number z by i is equivalent to rotating the image of z in Argand plane by 90º about origin, anticlockwise, as |z| = |iz| and

Multiplying a complex number z by ω is equivalent to rotating the image of z in Argand plane by 120º (or 240°) about origin anticlockwise, for |z| = |wz| (|w| = 1) and

ANGLES OF A TRIANGLE

If z1 z2 and z3 be the affices of vertices A, B and C of a triangle ABC described in counterclockwise sense. Then

Similarly relations with other vertical angles can be given.

IMPORTANT RESULTS ABOUT TRIANGLES

If z1, z2 , z3 are the vertices of a triangle then

Centroid z is given by
Incentre I (z) of the ΔABC is given by
Circumcentre O(z) of theΔABC is given by

Orthocentre H(z) of ΔABC is given by

The centroid G lies on the segment joining the orthocentre H and the circumcentre O of the triangle and divides internally in ratio 2 : 1, i.e

Area of the ΔABC is given by the modulus of
Triangle ABC is equilateral if and only if

EQUATION OF STRAIGHT LINE THROUGH TWO POINTS Z₁ AND Z2

Let variable point z be a point on this line then

Let a constant complex number then Also is purely real constant number, say b then the above equation is

It is called the general equation of a straight line

The complex equation represents a straight line in complex plane where 'a' is a complex number and 'b' is a real number. The complex slope of the line is given by .
The equation of the perpendicular bisector of the line segment joining the points A(z1) and B(z2) is

IMPORTANT RESULTS

The complex slope of line joining points A (z1) and B(z2) is define as
Two lines with complex slopes and are parallel if and perpendicular if
The length of perpendicular from a point to the line is given by

EQUATION OF A CIRCLE

Consider a circle with centre C having affix z0 and radius r.

For any point P(z) on this circle CP = r

i.e.

.....(1)

where, r is a positive real number

represents the region inside the circle given by (1)

represents the region outside the circle given by (1).

General equation of a circle

Consider the equation of a circle

Let

a constant complex number and

a constant real number then the above equation becomes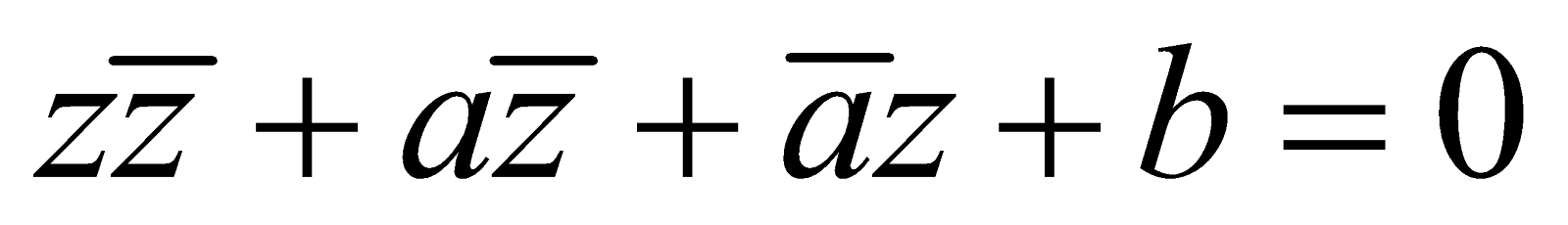

It is called the general equation of circle .

Hence the complex equation

represents a circle in complex plane where 'a' is a complex number and 'b' is a real number. The centre of the circle is a point with affix '–a' and the radius is given by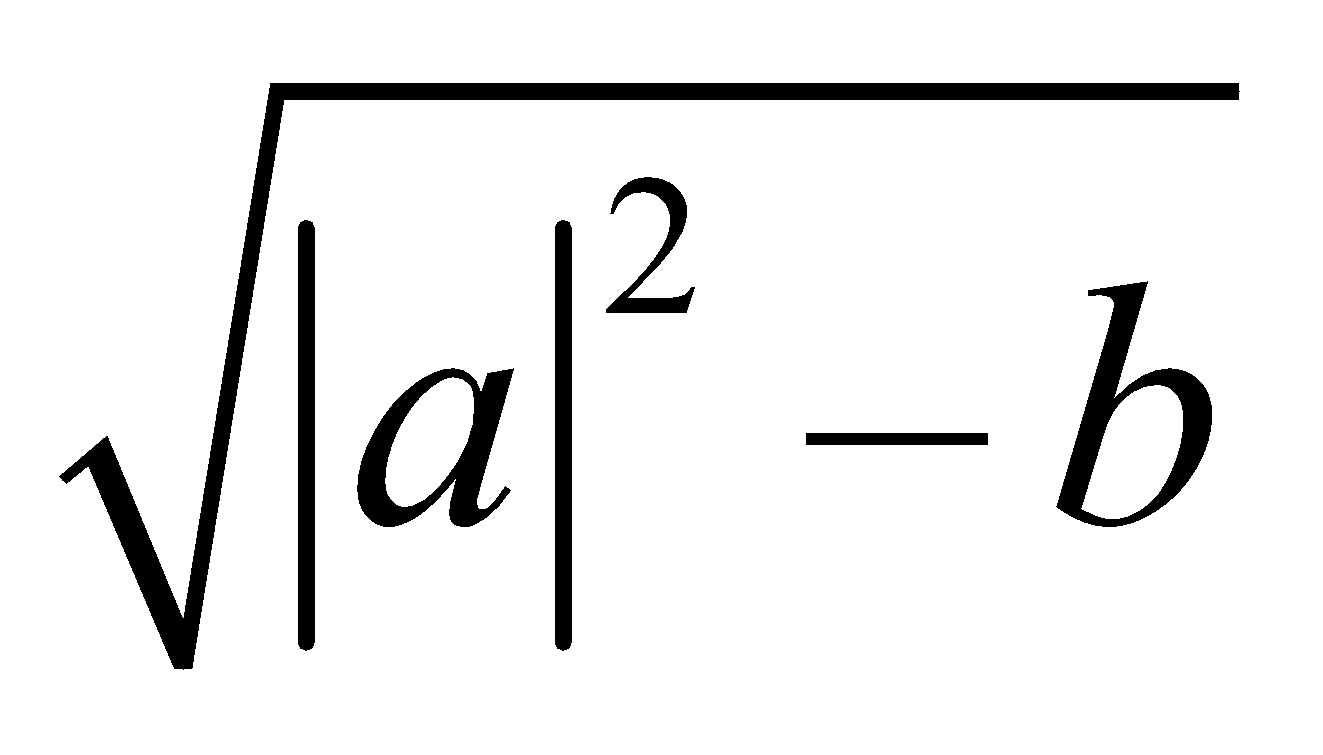

. For the existence of the circle

represents a circle in the complex plane which is described on a line as diameter having extremities z1 and z2.

SOME LOCI IN COMPLEX PLANE

represents a line starting from the origin (excluding origin) and making an angle with the real axis.

represents a line starting from the point z0 (excluding the point z0) and making an angle with the real axis.

If z1 and z2 are two fixed points then locus of z, satisfying is the perpendicular bisector of the segment joining and
The complex equation where 'a' is positive real number represents an ellipse in complex plane, z1 and z2 are affices of two foci of ellipse. If then represents the line segment joining z1 and z2

then the equation does not represent any curve

The complex equation .where , and 'a' is positive real number, represents a hyperbola in complex plane, z1 and z2 are affices of two foci of hyperbola.