INVERSE TRIGONOMETRIC FUNCTIONS
INVERSE TRIGONOMETRIC FUNCTIONS
A function f : A→B is invertible if and only if it is a bijection. The inverse of f is denoted by f–1 and is defined as
Clearly, domain of f–1 = range of f and range of f–1= domain of f.
Consider the sine function with domain R and range [–1, 1]. Clearly this function is not a bijection and so is not invertible. If we restrict the domain of the function in such a way that it become one-one, then it would become invertible. If we consider sine as a function with domain  and co-domain [–1, 1] then it is a bijection and therefore invertible. The inverse of sine function is defined as
and co-domain [–1, 1] then it is a bijection and therefore invertible. The inverse of sine function is defined as 
 where
where  and x ∈ [–1, 1]
and x ∈ [–1, 1]
The sine function is also a bijection with domains ,
,  etc., and the same range,
etc., and the same range,
Thus sin–1 x has infinitely many values for given x ∈ [–1 1]. However there is one value among these values which lies in the interval  . This value is called the PRINCIPAL VALUE.
. This value is called the PRINCIPAL VALUE.
DOMAIN AND RANGE (PRINCIPAL VALUE) OF INVERSE TRIGONOMETRIC FUNCTION
Function Domain Range
sin–1 x [–1, 1] 
cos–1 x [–1, 1] [0 , π]
tan–1 x (–∞, ∞) 
cot–1 x (–∞, ∞) (0 , π)
sec–1 x (–∞ ,−1) ∪ (1, ∞) 
cosec–1 x (–∞ , −1) ∪ (1 , ∞) 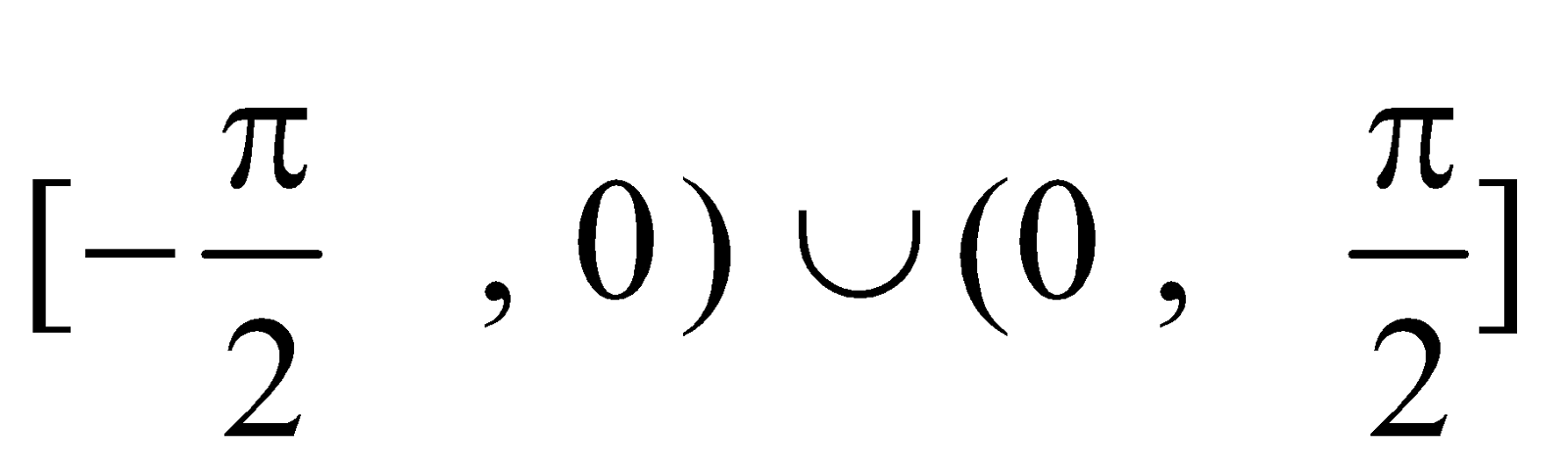
Thus,
sin–1 x = θ ⇔ x = sin θ, where and
and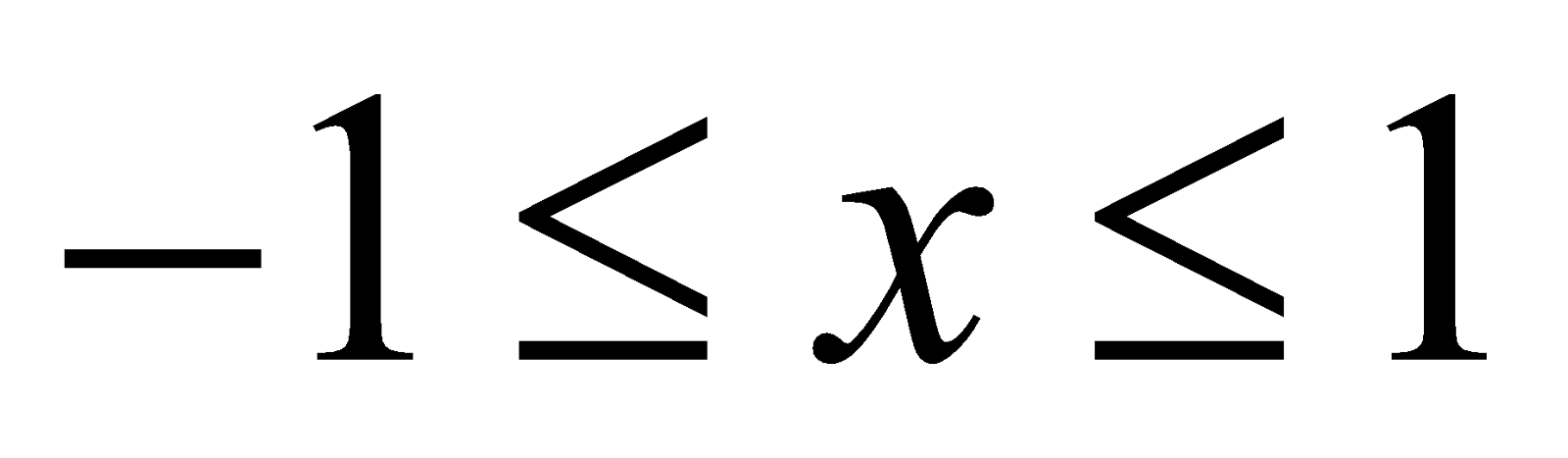
sin–1 x = θ ⇔ x = sin θ, where
cos–1 x = θ ⇔ x = cos θ, where  and 0 ≤ θ ≤ π
and 0 ≤ θ ≤ π
tan–1 x = θ ⇔ x = tan θ, where – ∞ < x < ∞ and 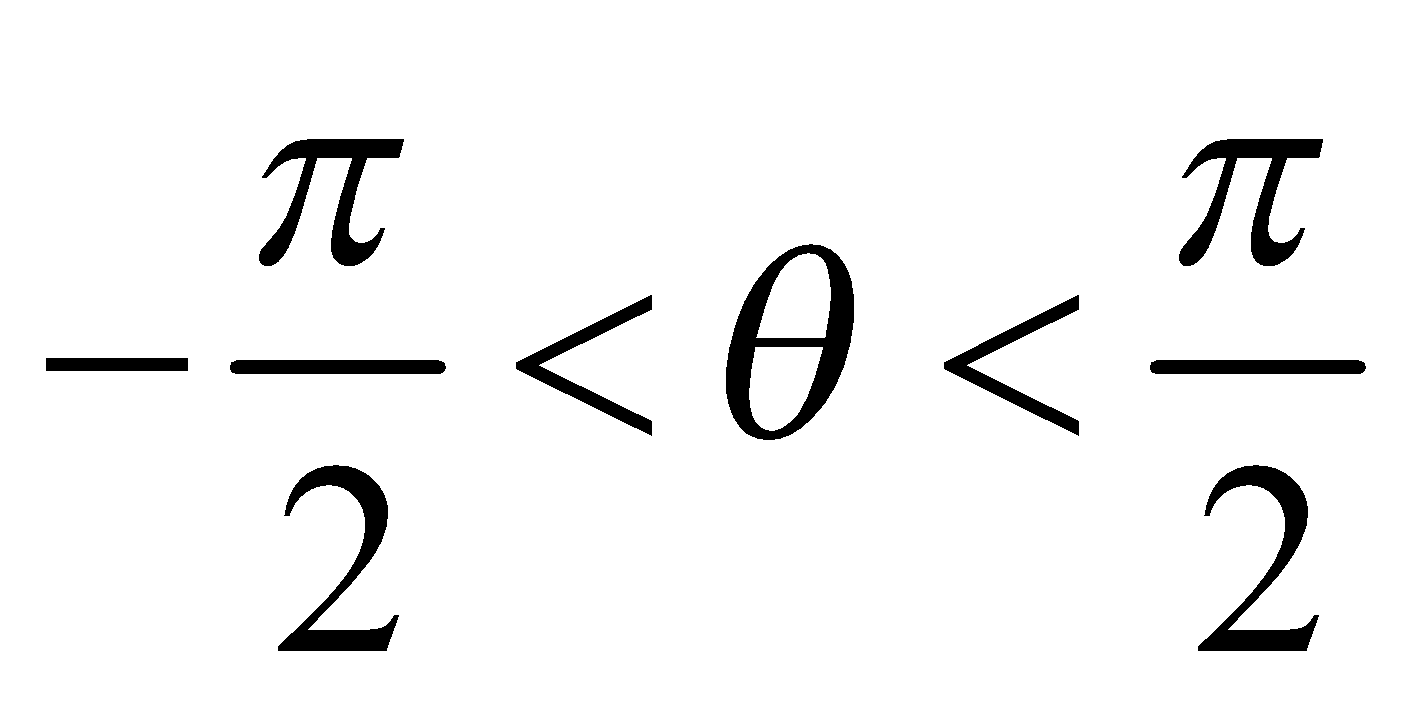
cot–1 x = θ ⇔ x = cot θ, where −∞ < x < ∞ and 0 < θ < π
sec–1 x = θ ⇔ x = sec θ, where – ∞ < x ≤ –1 or 1 ≤ x < ∞ and 
cosec–1 x = θ ⇔ x = cosec θ, where – ∞ < x ≤ –1 or 1 ≤ x < ∞ and 
PROPERTIES OF INVERSE TRIGONOMETRIC FUNCTIONS
1. (i) sin–1 (sin θ) = θ and sin (sin–1 x) = x. Provided that –1 ≤ x ≤ 1 and .
.
(ii)  . Provided that
. Provided that 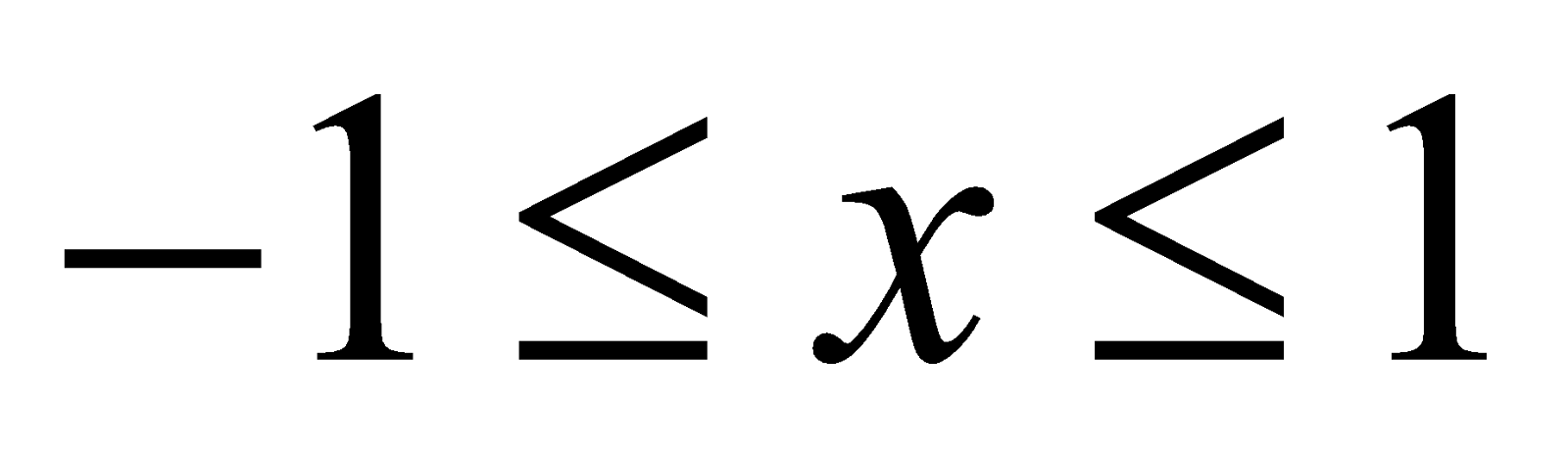 and
and  .
.
(iii)  . Provided that
. Provided that  .
.
(iv) 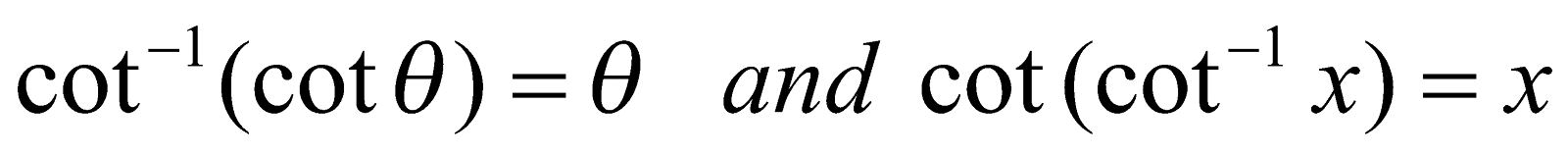 . Provided that
. Provided that 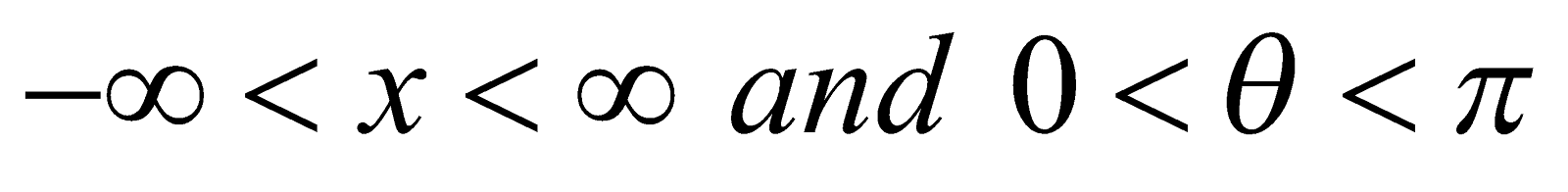 .
.
(v)  .
.
(vi)  where θ and x in (v) and (vi) satisfy the corresponding domains and range.
where θ and x in (v) and (vi) satisfy the corresponding domains and range.
2. (i) 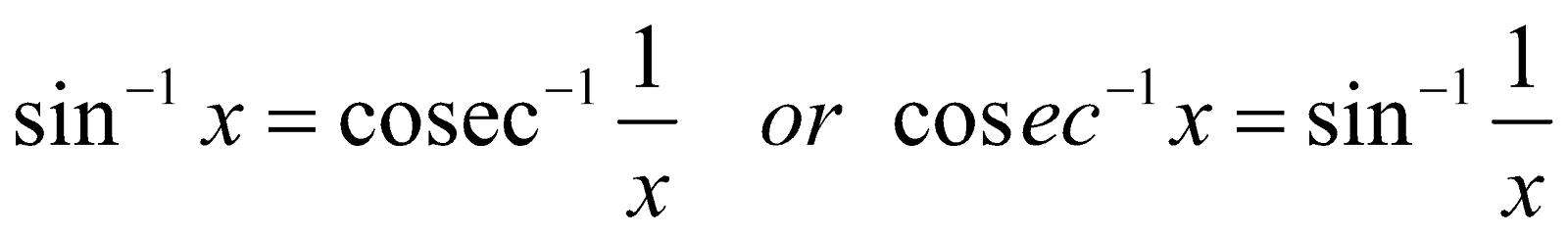
(ii) 
(iii)  if x > 0 and
if x > 0 and
3. (i) 

(ii) 
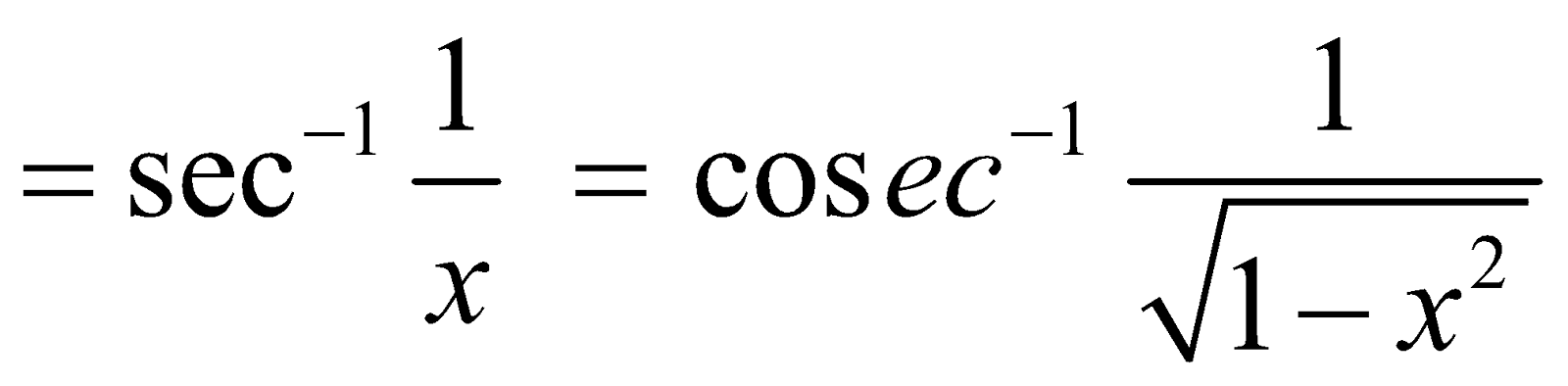
(iii) 

4. (i)  where – 1 ≤ x ≤ 1
where – 1 ≤ x ≤ 1
(ii)  where – ∞ < x < ∞.
where – ∞ < x < ∞.
(iii) 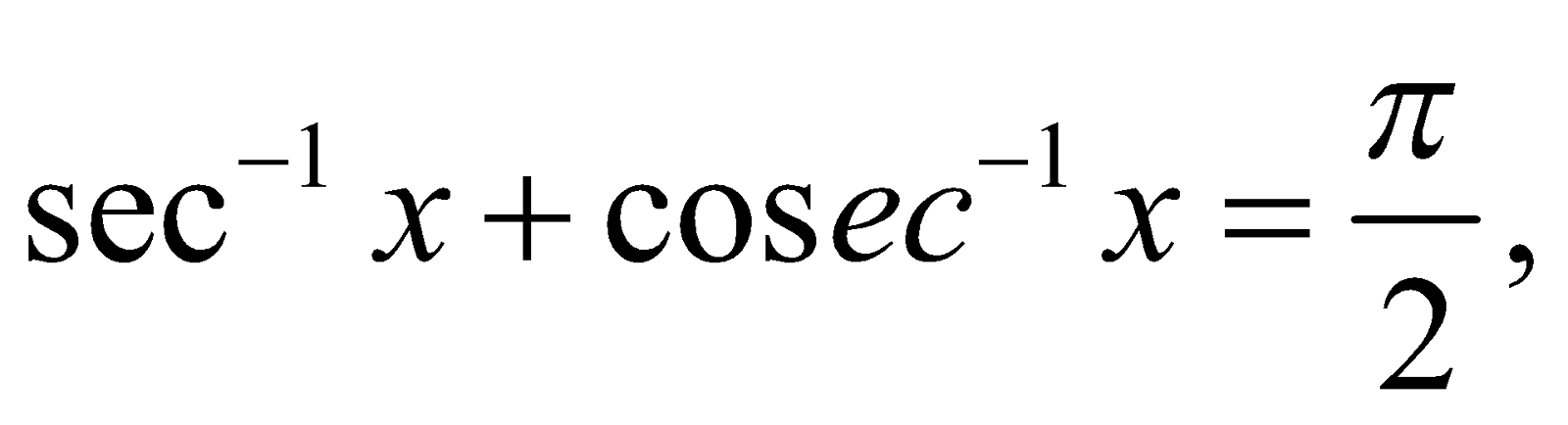 where x ≤ –1 or x ≥ 1.
where x ≤ –1 or x ≥ 1.
5. (a) 
(b) 
(c) 
(d) 
(e) 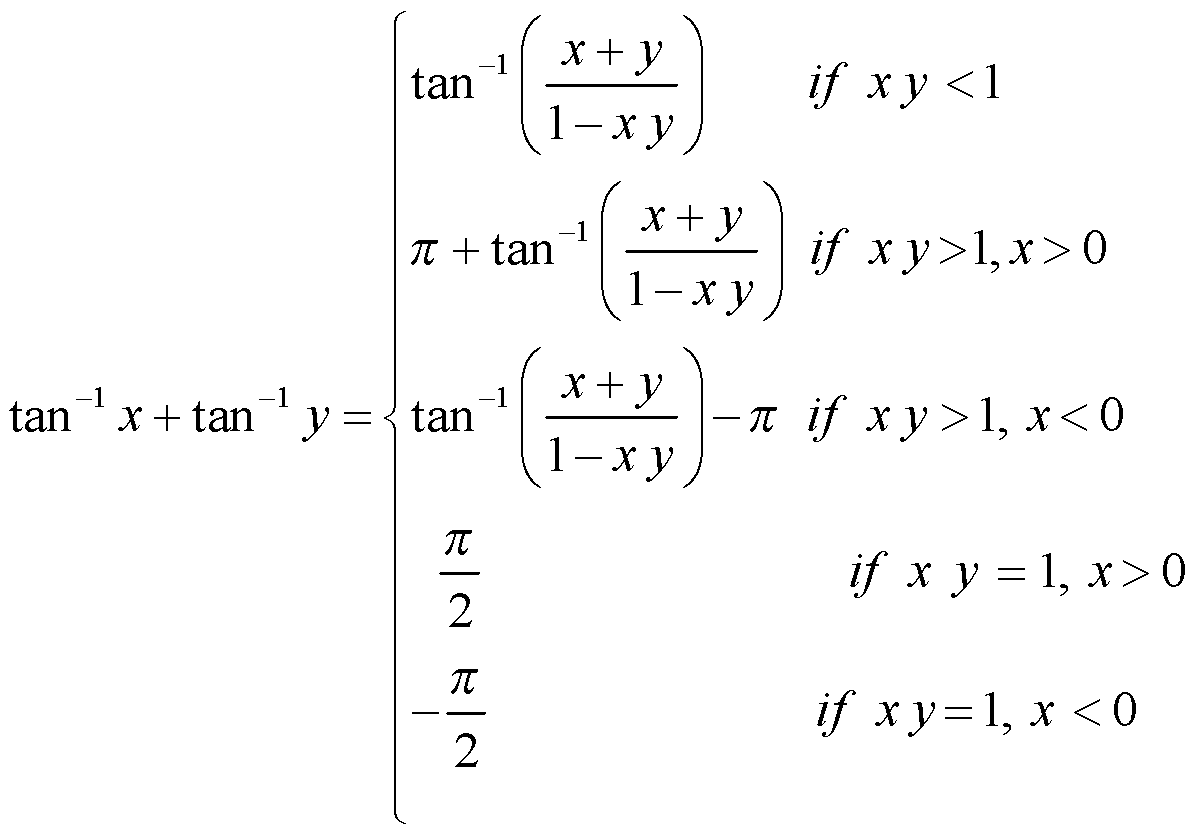
(f) 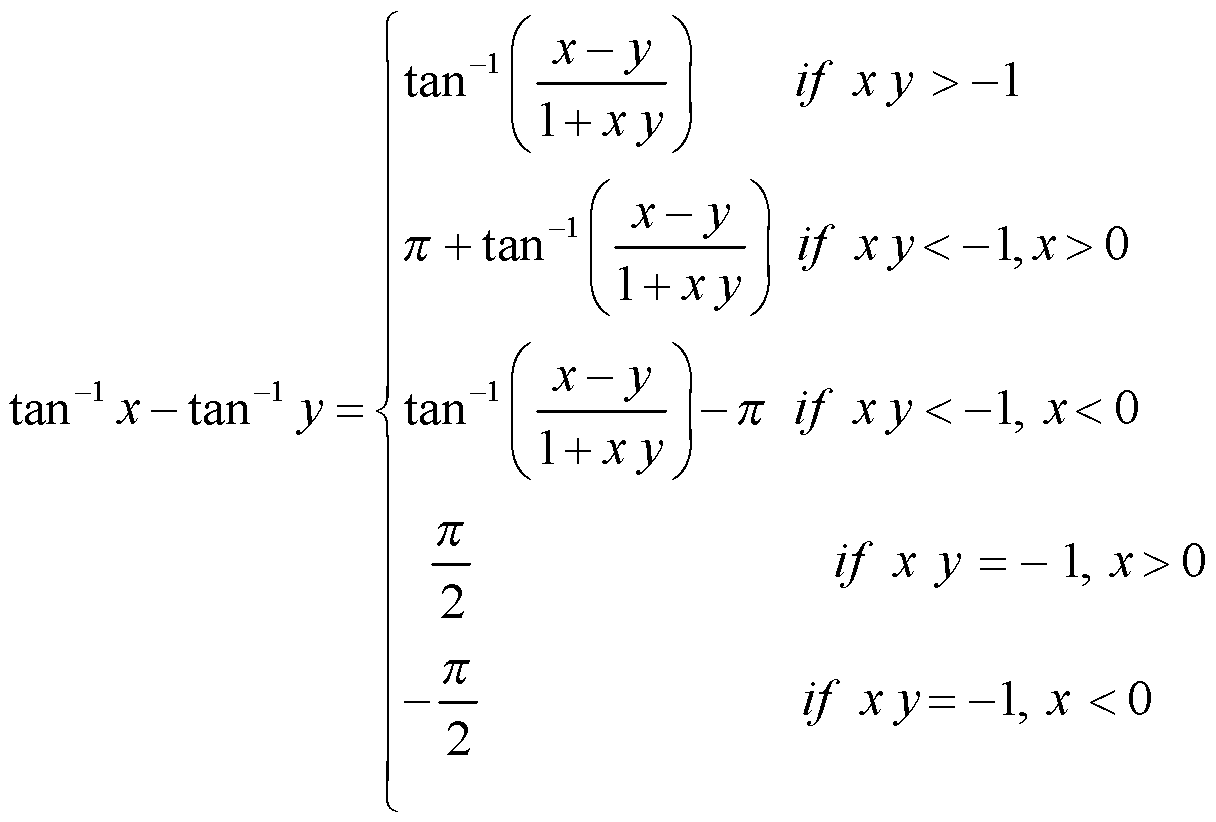
(g) 
(h) 
(i) 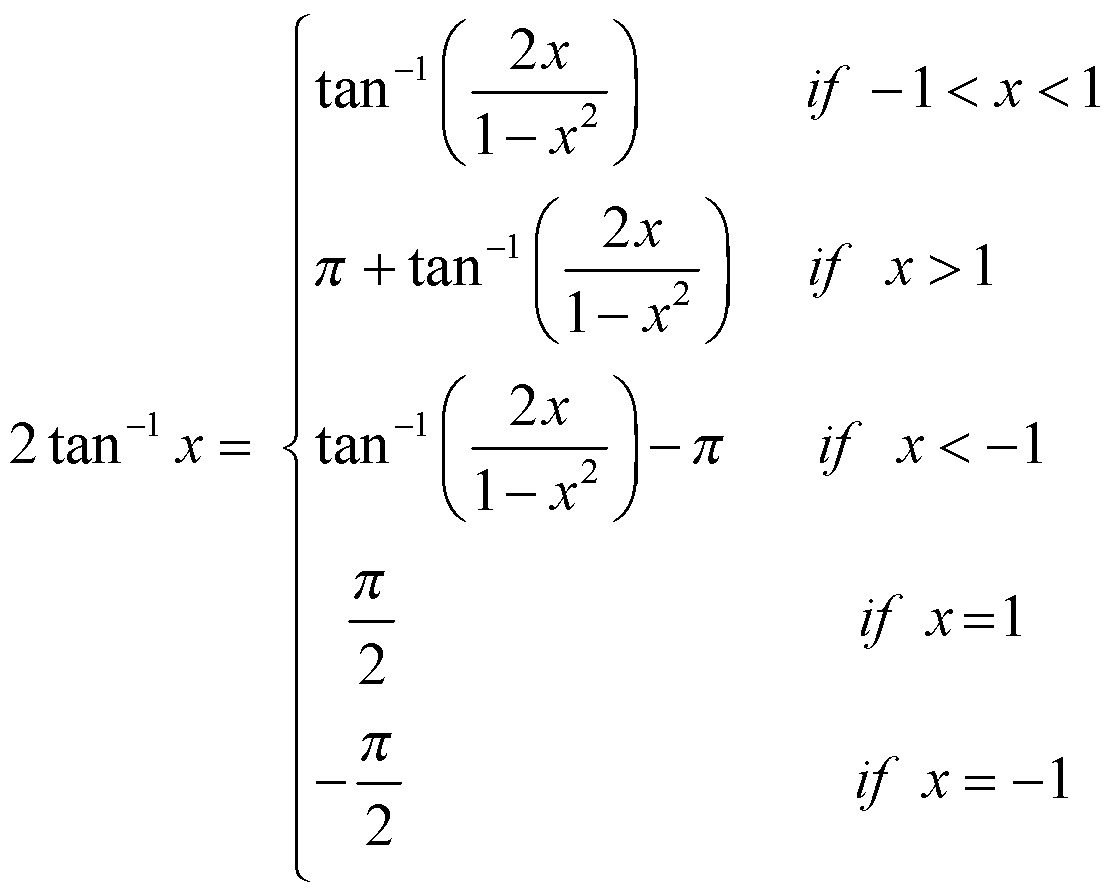
(j) 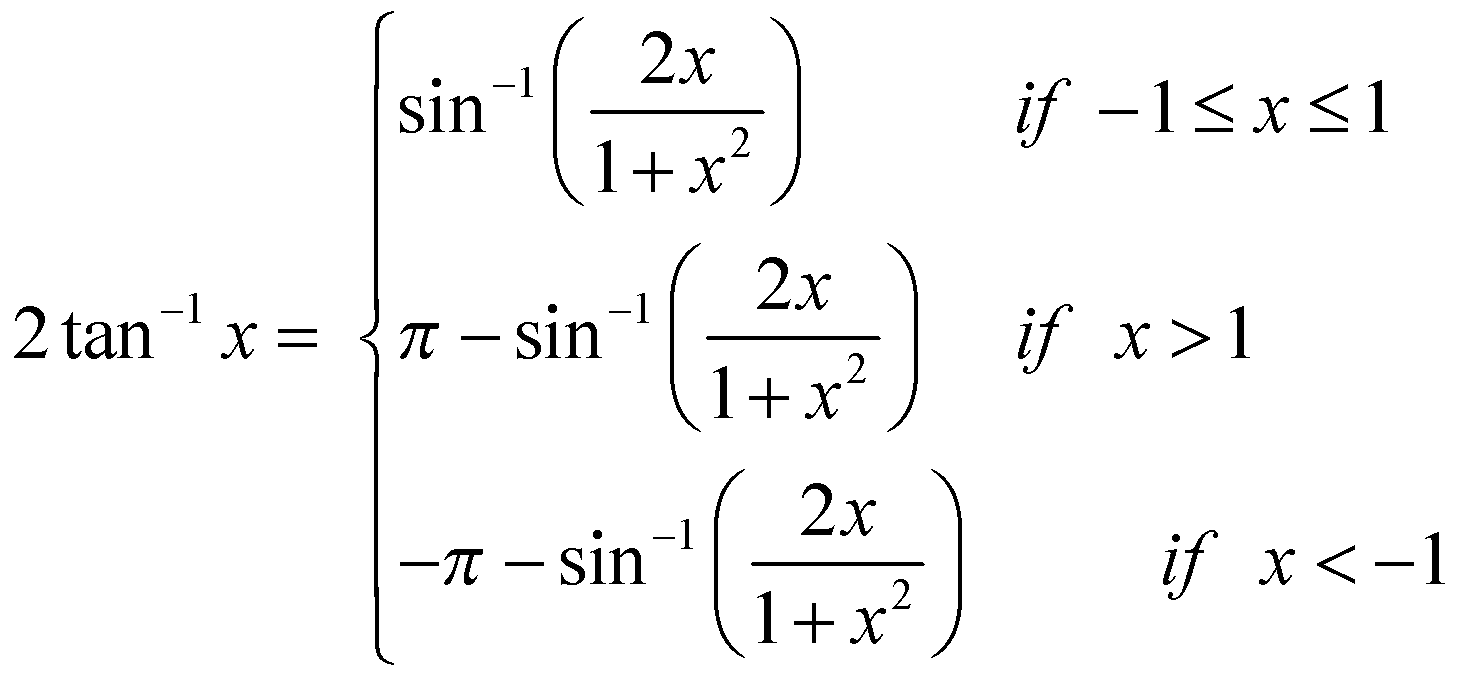
(k) 
6. (i) 
(ii) 
(iii) 
(iv) 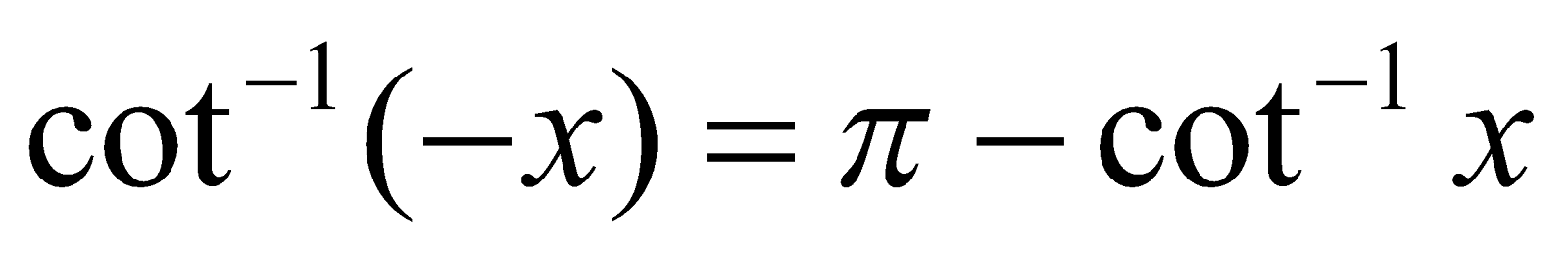
7. (i) 
(ii) 
(iii) 
8. 
SOLVING EQUATIONS CONTAINING INVERSE TRIGONOMETRIC FUNCTIONS
The unknown involved in the equation is evaluated with the help of formulae we previously discussed. Following procedure can be applied for the solution of these equations.
WORKING PROCEDURE
- If the equation involved contains, terms of different inverse functions then try to reduce in a single term
- Convert the inverse functions is LHS and RHS to same if not so and then cancel.
- In general we do not apply restrictions on x while using above formulae so there is always chance that some erroneous roots might occur.
- Check the roots by substituting in the original equation and discard if any of them do not satisfy the equation.







