STATES OF MATTER
STATES OF MATTER
The three important states of the matter are (i) Solid state (ii) Liquid state (iii) Gaseous state, which can exist together at a particular temperature and pressure e.g. water has three states in equilibrium at 4.58 mm and 0.0098ºC.
PLASMA STATE : It is the gaseous mixture of electrons and positive ions existing at extremely high temperatures (in the interior of stars) or internal electrical fields in discharge tubes.
SINGLE SUPER ATOM STATE : At extremely low temperature, all atoms lose their identity and get condensed into a single entity behaving like a single super atom.
MEASURABLE PROPERTIES OF GASES
Four measurable properties are:
- Mass : It is expressed in grams or kg. 1 kg=103 g moles of
gas =
- Volume : It is equal to the volume of the container and is expressed in terms of litres (L), millilitres (ml), cubic centimeters , cubic meters (m3) or cubic decimeters (dm3).
- Pressure : It is equal to force per unit area and expressed in the units such as atmosphere, millimetres (mm), centimetres (cm), torr, bar etc. SI unit of pressure is pascal (Pa) or kilopascal (kPa)
- Temperature : It is measured in celsius scale (°C)or in Kelvin scale (K). SI unit of temperature is Kelvin (K) or absolute degree T (K) =
GAS LAWS
BOYLE’S LAW
The volume of a given mass of a gas is inversely proportional to its pressure at constant temperature.
Value of k depends on mass, temperature and nature of gas.
When mass and temperature are the same we have 
ISOTHERMS
Graphs of V vs P or PV vs P at constant temperature are known as Isotherm.
Graphical representation of Boyle's law
CHARLE’S LAW
The volume of the given mass of a gas increases or decreases by  of its volume at 0°C for each degree rise or fall of temperature at constant pressure.
of its volume at 0°C for each degree rise or fall of temperature at constant pressure.
or
The volume of a given mass of a gas is directly proportional to the absolute temperature at constant pressure.
ABSOLUTE ZERO
If in the above equation we put the value of t as –273.15 ºC the volume of the gas will be zero. It means gas will not exist, which is not possible. In fact all gases get liquified before this temperature is reached. This hypothetical or imaginary temperature at which the gases occupy zero volume is called absolute zero.
ISOBARS
A graph of V vs T at constant pressure is known as Isobar.
GRAPHICAL REPRESENTATION OF CHARLE’S LAW
GAY LUSSAC’S LAW : (AMANTON’S LAW)
The pressure of a given mass, of gas increases or decreases by  of its pressure at 0°C for each degree rise or fall of temperature at constant volume.
of its pressure at 0°C for each degree rise or fall of temperature at constant volume.
or
The pressure of a given mass of a gas at constant volume is directly proportional to absolute temperature
ISOCHORES
A graph of P vs T at constant volume is known as Isochore
GRAPHICAL REPRESENTATION OF GAY LUSSAC’S LAW
AVOGADRO’S LAW
The volume of a gas is directly proportional to number of molecules or moles at constant temperature and pressure.
GRAPHICAL REPRESENTATION OF AVOGADRO’S LAW
IDEAL GAS EQUATION
. 
This is known as ideal gas equation. R is known as universal gas constant.
IDEAL GAS
The gas which obeys the equation at every temperature and pressure range strictly.
REAL OR NON-IDEAL GASES
Since none of the gases present in universe strictly obey the equation , hence they are known as real or non ideal gases. Real gases behave ideally at low P and high T.
, hence they are known as real or non ideal gases. Real gases behave ideally at low P and high T.
DENSITY OF A GAS
We have  ,
, 
Further, 
The above equation shows that density of a gas depends on P and T.
Unit of density of gas :
It is usually expressed in gm/ litre
VAPOUR DENSITY (V.D.)
It is the ratio under similar conditions of P and T
Unit of vapour density : It is a ratio and has no unit.
NATURE OF GAS CONSTANT, (R)
= Work done per degree per mole
Deviation from ideal behaviour in terms of compressibility factor Z
Deviation from ideal behaviour in terms of PV-P curve
NUMERICAL VALUE OF R
As the work can be expressed in different systems of units, R will have different values.
- In litre - atmosphere :
At NTP, P = 1atm, V=22.4 litre and T= 273.15K
- In cgs system :
P = 1 atm = 1×76×13.6×980 dyne cm-2; V = 22400 cm3;
T = 273.15 K
T = 273.15 K
- In mks or SI units :
Unit of R is JouleK–1
107 ergs = 1 Joule or R = 8.314 Joule K–1
NTP OR STP AND SATP
Normal or standard temperature & pressure means 0°C or 273.15 K and 1 atm pressure.
Normal boiling : At 1 atm pressure the boiling temperature is called Normal boiling point.
Standard boiling point : At 1 bar pressure the boiling temperature is called standard boiling point.
Normal boiling point of water is 100 °C (373.13 K)
Standard boiling point of water is 99.6 °C (372.6K)
Standard temperature and pressure (STP)
273.15 K(0 °C) temperature
1 bar (105 pascal) pressure
Molar volume at STP = 22.71098 L mol–1
Normal temperature and pressure (NTP)
273.15 K(0 °C) temperature
1 atom (1.01325 pascal) pressure
Molar volume at NTP = 22.413996 L mol–1
Standard ambient temperature and pressure (SATP)
298.15 K (25 °C) temperature
1 bar (105 pascal) pressure
Molar volume at SATP = 22.784 L mol–1
BOLTZMANN CONSTANT (k)
It is the gas constant per molecule thus  ; Where R=gas constant., N0= Avogadro number.
; Where R=gas constant., N0= Avogadro number.
Value of 
DALTON’S LAW OF PARTIAL PRESSURE
At constant temperature the total pressure, exerted by a mixture of non reacting gases, is the sum of partial pressure of each gas
Partial pressure p of a gas = mole fraction of the gas × total pressure.
For a gas A, pA = xA × P
If n1,n2,and n3 are moles of non reacting gases filled in a vessel of volume V at temperature T.
The total pressure P is given by 
This is the equation of state of a gaseous mixture.
RELATIONSHIP BETWEEN TOTAL PRESSURE AND INDIVIDUAL PRESSURE
On mixing of gases at constant temperature. If a gas A at pressure P1 and volume V1 is mixed with gas B at pressure p2 and volume V2 at same temperature, then
Total pressure, 
AQUEOUS TENSION
It is the pressure exerted by water vapour at a particular temperature. It depends upon temperature.
PRESSURE OF A DRY GAS
When a gas is collected over water, its observed pressure is equal to the sum of the pressure of dry gas and the pressure of water vapour (aqueous tension), then
Pressure of dry gas = pressure of moist gas – aqueous tension
DIFFUSION
The tendency of every gaseous substance to distribute itself uniformly throughout the available space is known as diffusion. It also takes place through a porous vessel.
EFFUSION
The movement of a gas through a small hole when it is subjected to pressure is known as effusion.
GRAHAM’S LAW OF DIFFUSION (OR EFFUSION)
At constant temperature and pressure, the rate of diffusion or effusion of a gas is inversely proportional to the square root of its density.
Rate of diffusion ∝ 
If  and
and  are rates of diffusion of two gases and and their respective densities then,
are rates of diffusion of two gases and and their respective densities then,
Rate of diffusion
If volume diffused is same 
If time of diffusion is same 
Effect of pressure on the rate of diffusion.
Rate of diffusion ∝ pressure, therefore, 
APPLICATIONS OF GRAHAM’S LAW OF DIFFUSION
- Determination of densities and molecular masses of unknown gases.
- Separating the gases having different densities.
- Separation of Isotopes
ATMOLYSIS
The phenomenon of separation of a mixture of gases due to difference in their rates of diffusion is called atmolysis.
KINETIC THEORY OF GASES
Postulates of kinetic theory of gases.
- A gas consists of large number of tiny particles called molecules.
- Volume occupied by gas molecules, is negligible as compared to the total volume of gas.
- There is continuous rapid random motion of gas molecules. The molecules collide with each other and against walls of container.
- The molecules are perfectly elastic bodies and there is no loss of kinetic energy during collisions.
- There are no attractive forces between the molecules of gas.
- The pressure exerted by a gas is due to bombardment of gas molecules against the walls of the container.
- The different molecules possess different velocities and hence different energies. The average K.E. is directly proportional to absolute temperature.
KINETIC GAS EQUATION
Based upon the postulates of Kinetic theory of gases, the kinetic gas equation is
where m = mass of a gas molecule, N= number of molecules,
U= Root mean square velocity.
U= Root mean square velocity.
KINETIC ENERGY OF GAS
It can be obtained from kinetic gas equation
KE of one molecule 
- KE of n moles of gas = 3/2 nRT
- At absolute zero, KE is zero
MAXWELL’S GENERALISATION
Kinetic Energy of translation of ideal gas is directly proportional to absolute temperature of gas or its pressure and is independent of the nature of gas.
THERMAL MOTION
The molecular velocity of a gas is proportional to square root of the absolute temperature. The molecular motion is called thermal motion of molecules.
CALCULATION OF MOLECULAR VELOCITIES OF GASES
- Calculation of velocity when temperature alone is given :
From Kinetic gas equation,
- Calculation of velocity at NTP
It is given by the formula, 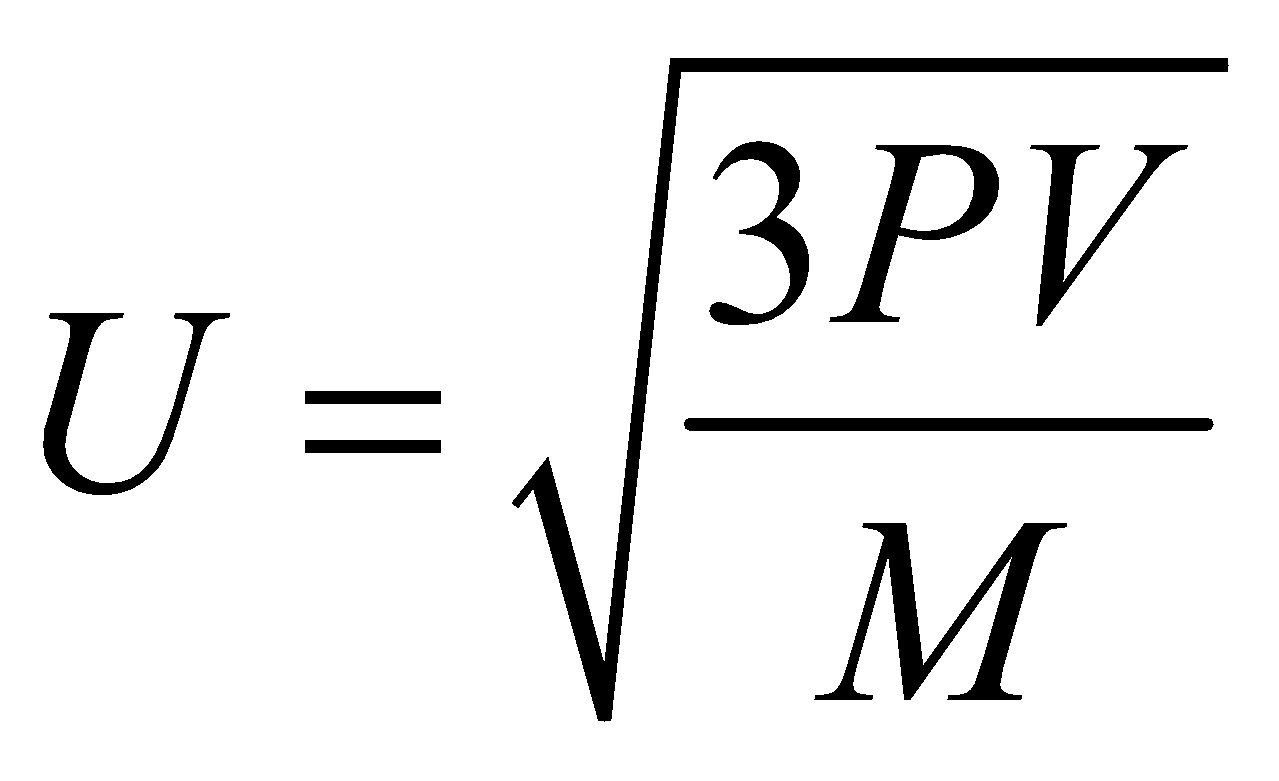
AT NTP, P=dynes cm-2, (molar volume)
- Calculation of velocity when pressure and density are given.
It is given by the following formula,
- Calulation of velocity when pressure and temperature are given but are not the same as NTP
MAXWELL’S DISTRIBUTION OF VELOCITIES
The molecules present in a given sample of gas move with different velocities in all possible directions. Velocities and directions of molecules keep on changing due to intermolecular collisions. Hence it is impossible to find out the individual velocity of each molecule. It is however possible to predict fraction ( ) of the total number of molecules having specific velocities at a particular temperature. As shown by the curve,
) of the total number of molecules having specific velocities at a particular temperature. As shown by the curve,
The gases show ideal behavior at low presence/large volume. Since the volume of molecules can be neglected and at high temperature since intermolecular forces decrease.
Fraction of molecules having very small or very high velocities is very low. No molecule has zero velocity. Fraction of molecules possessing a particular velocity at a particular temperature is constant. The different velocities possessed by gas molecules are:
- Most probable velocity (
) : It is the velocity possessed by maximum fraction of gas molecules at a particular temperature
Mathematically, 
- Average velocity (
) : This is the average of the different velocities of all the molecules.
where c1,c2,c3 etc. are individual velocities of n1,n2,n3 molecules.
Mathematically,  =
=
- Root mean square velocity (U) : It is the square root of the mean of the square of the different velocities of the molecules
Mathematically, U = 
RELATIONSHIP BETWEEN DIFFERENT TYPES OF VELOCITIES :
= =
=
Calculation of root mean square velocity (Urms) : As already discussed, the Urms can be calculated by any of the following relations:
Urms =
Ratio of Urms for two different gases at the same temperature
Ratio of Urms for the same gas at different temperature
EFFECT OF TEMPERATURE ON DISTRIBUTION OF MOLECULAR VELOCITIES
Most probable velocity increases with the rise in temperature but fraction of molecules possessing such velocity decreases.
Deviation from ideal behaviour of gas :
At high pressure and low temperature the gases deviate considerably from the ideal behaviour. Deviation can be expressed in terms of compressibility factor (Z), expressed as 
In case of ideal gas, 
In case of real gas, 
Negative deviation
In such case, Z < 1, gas is more compressible.
Positive deviation
In such case, Z >1, gas is less compressible.
Factors affecting the deviation :
The factors affecting the deviation are:
- Nature of the gas : In general, the most easily liquefiable and highly soluble gases show larger deviation.
- Pressure : The deviation is more at high pressure. CO2 and N2 show negative deviation at low pressure and positive deviation at high pressure.
- Temperature : The deviation is more at low temperature. H2 and He always show positive deviations at 0°C
BOYLE’S TEMPERATURE
Temperature at which a real gas exhibits ideal behaviour for considerable range of pressure is called Boyle’s temperature. Mathematically,
- Boyle temperature is different for different gases
- Below Boyle’s temperature a gas shows negative deviation.
- Above Boyle’s temperature a gas shows positive deviation
CAUSE OF DEVIATION FROM THE IDEAL BEHAVIOUR
It is due to two faulty assumptions of Kinetic theory of gases particularly not valid at high pressure and low temperature.
- Volume occupied by the gas molecules is negligible as compared to the total volume of gas.
- There are no attractive forces between the gas molecules.
VAN DER WAAL'S EQUATION
After volume & pressure correction, van der Waals obtained the following equation for n moles of a gas
Excluded volume or co-volume, (b)
The constant b in van der Waal's equation is known as excluded volume or co-volume. It is nearly four times the actual volume occupied by the gas molecules.
Excluded or co-volume (b) = 4 × actual volume of gas molecules.
Magnitude of attractive forces between gas molecules (a)
It is given by van der Waals constant ‘a’. Different gases have different value for ‘a’.
(i) The greater the value of ‘a’, the greater the strength of van der Waals forces.
(ii) The greater the value of ‘a’, the greater is the ease with which a gas can be liquefied.
Units for Van Der Waal's constant:
Pressure correction,
Volume correction, 
DISCUSSION OF VAN DER WAAL’S EQUATION
Van der Waal’s equation for one mole of gas
- At low pressure and ordinary temperature : V is very large and b can be neglected then
or ; 
Therefore Z is less than 1.
Hence at low pressure the gases show negative deviation.
- At high pressure and ordinary temperature : At high pressure, volume V will be quite small. The quantity
become negligible but ‘b’ cannot be ignored.
or  ; Therefore Z is more than 1.
; Therefore Z is more than 1.
At high pressure the gases show positive deviation
Note : At some intermediate range of pressure and ordinary temperature the gas shows the ideal behaviour.
- At low pressure and high temperature : The effect of
and b is negligible. We have
or
Therefore Z = 1. Hence gas shows ideal behaviour.
- Exceptional behaviour of Hydrogen and Helium :
Due to their small size, the attractive forces between the molecules are too small,is negligible, then
Hence they always show positive deviation.
LIMITATION OF VAN DER WAAL’S EQUATION
There is specific range of temperature and pressure, to apply the equation. It deviates at too high pressure and too low temperature.
Other equations of states :
- Dieterici equation :
- Berthelot’s equation :
- Clausius equation :
Where c is a new constant
- Kammerling onne's equation (virial equation):
- The coefficients A,B,C,D, etc are known as first, second, third, fourth virial coefficients
- At low pressure only A (which is equal to RT) is important, the others cancel out.
- A is always positive and increases with rise of temperature.
- At Boyle temperature B=0
- Relation between B and van der Waals constant is
CRITICAL PHENOMENON AND LIQUEFACTION OF GASES
Increase of pressure and decrease of temperature tend to cause liquefaction of gases. The effect of temperature is, however more important.
CRITICAL TEMPERATURE (TC)
It may be defined as the temperature above which no gas can be liquefied howsoever high the pressure may be, critical temperature of CO2 is 31.1°C.
Critical temperature (Tc) of some gases,
He 5.2 CO2 304.1 CH4 190.2
H2 33.2 N2O 309.6 HCl 324.5
N2 126.0 NH3 405.5 H2S 373.5
CO 134.4 Cl2 417.1 Ar 150.7
O2 154.3 SO2 430.3
CRITICAL PRESSURE (PC)
At critical temperature the pressure needed to liquefy a gas is known as critical pressure.
CRITICAL VOLUME (VC)
The volume occupied by one mole of a gas at critical temperature and critical pressure is known as critical volume.
Relationship between critical constants and van der Waal’s constant:
Relationship between boiling point and critical temperature:
Boiling point = critical temperature.
critical temperature.
Compressibility for 1 mole of gas at critical state:
JOULE THOMSON EFFECT
When a gas under high pressure is allowed to expand adiabatically into a region of extremely low pressure, it suffers change of temperature. The phenomenon is known as Joule -Thomson effect.
CONDITION FOR JOULE-THOMSON EFFECT (INVERSION TEMPERATURE)
In Joule -Thomson effect, cooling is observed only if the gas is present below certain temperature known as inversion temperature, Ti. It is characteristic of each gas and related to Van der Waal’s constant a and b as,
At exact inversion temperature there is no Joule-Thomson effect. Above inversion temperature, there is heating during Joule-Thomson effect. Below inversion temperature there is cooling during Joule-Thomson effect.
Inversion temperature for hydrogen = –80°C and for He = –240°C. Joule-Thomson effect is zero in an ideal gas and enthalpy remains constant. When an ideal gas expands in vacuum, it does no work i.e. W=0 ; (Adiabatic condition). Hence internal energy of a given quantity of an ideal gas at constant temperature is independent of its volume.
Thermodynamically an ideal gas may be defined by following the equations.
- PV = constant, at constant temperature.
JOULE-THOMSON COEFFICIENT ( ) :
) :
The temperature change produced per atmosphere drop in pressure under constant enthalpy conditions on passing a gas through the porous plug is called Joule-Thomson coefficient
The quantity  is called Joule -Thomson coefficient.
is called Joule -Thomson coefficient.
- Joule Thomson Coefficient
is positive for real gases, (cooling)
Or Joule Thomson Coefficient will be positive when 
- When Joule Thomson Coefficient
is negative, (heating)
Or Joule Thomson Coefficient will be negative when 
- When Joule Thomson Coefficient
is zero, (no heating or cooling)
Or Joule Thomson Coefficient will be zero when
Since a, b and R are constants, the sign of Joule-Thomson Coefficient will depend only upon the temperature at which the gas is being allowed to expand. The temperature at which the Joule-Thomson Coefficient changes sign is known as the inversion temperature.
LAW OF CORRESPONDING STATES
When the values of pressure, volume and temperature are expressed as fractions of the corresponding critical values we have. 
where , and are termed, the reduced pressure, the reduced volume and the reduced temperature respectively. If we replace P,V and T by Pc, Vc and Tc in van der Waal’s equation and put the values of Pc, Vc and Tc terms of a, b and R we get,
If the two substances have the same reduced temperature and the same reduced pressure, they will have the same reduced volume. The statement is known as the law of corresponding states.
HEAT CAPACITY OF SYSTEM
For gases it can be at constant volume or at constant pressure.
- Heat capacity at constant volume (CV) is defined as the increase in internal energy of a gas per degree rise of temperature.
- Heat capacity at constant pressure (Cp) is defined as increase in enthalpy of a gas per degree rise of temperature.
For one mole of gas, the heat capacities at constant volume and constant pressure are denoted by Cv and Cp and are termed as molar heat capacities.
RELATION BETWEEN CP AND CV
Cp– Cv = R
R = 1.987 cal or 8.314 Joule
R= PΔV = Work done by one mole of an ideal gas in expansion at constant pressure when heated through 1°C.
MOLAR HEAT CAPACITIES FOR POLYATOMIC GASES
The values  and
and  are for monoatomic gases like He, Ar etc. where the energy supplied increases translational kinetic energy only. In polyatomic gases heat supplied is utilised to increase vibrational and rotational energy also. Thus we have
are for monoatomic gases like He, Ar etc. where the energy supplied increases translational kinetic energy only. In polyatomic gases heat supplied is utilised to increase vibrational and rotational energy also. Thus we have
For monoatomic gas, x = 0, 
for diatomic gases, x = R, 
for triatomic gases,  ,
, 
COLLISION PROPERTIES
- Molecular diameter or collision diameter : The distance between the centers of the molecules at the point of their closest approach.
- Collision frequency (Z) : The number of collisions experienced by molecules per cc of a gas per second is known as collision frequency of gas,
N = number of molecules per cm3
At constant pressure, 
At constant temperature, 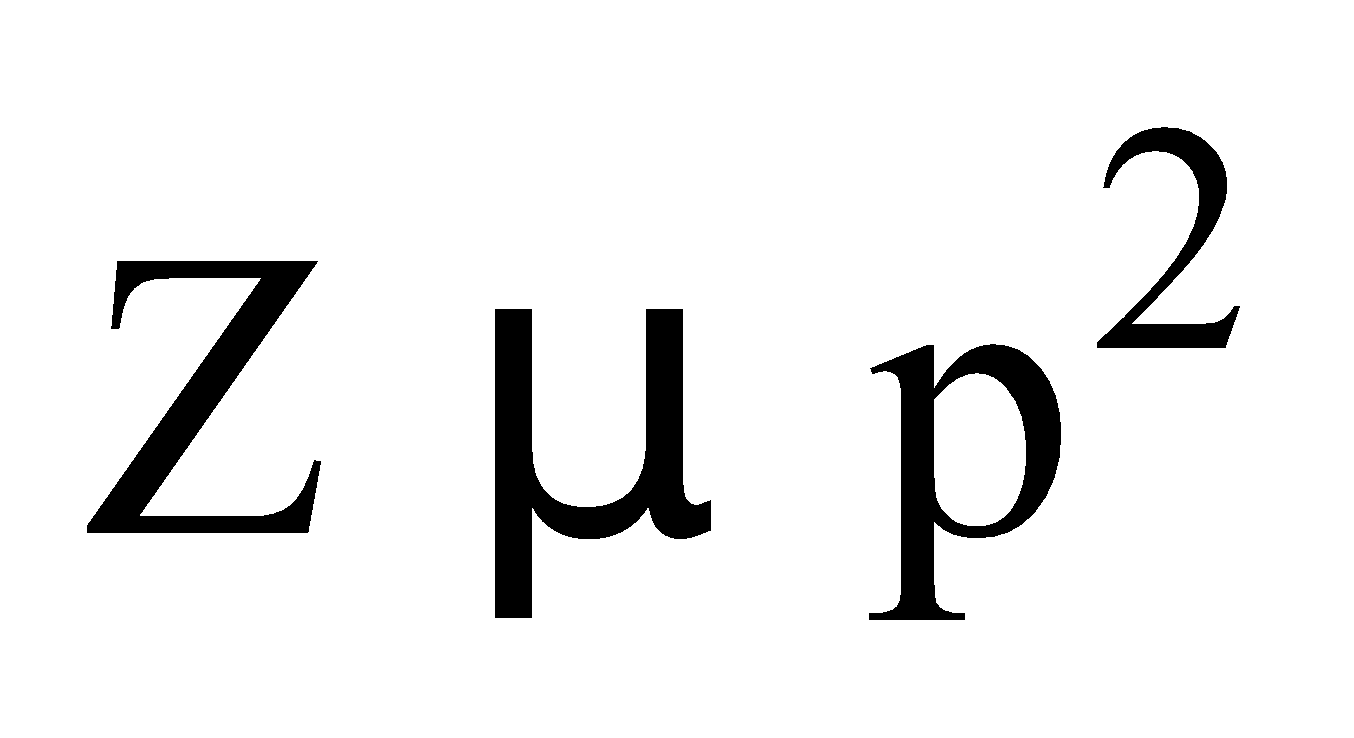
- Collision number (Z1) : Number of collisions undergone by a molecule with other molecules per second present in 1cm3.
Z1 = Collision number =
N = Number of molecules per unit volume of the gas
- Mean free path (l) : The average distance travelled by the molecule between two successive collisions
At constant pressure, 
At constant temperature, l
VOLUME COEFFICIENT
It is defined as the ratio of the increase in volume of the gas at constant pressure per degree rise of temperature to its volume at 0°C
V0 =Volume of a given mass of a gas at 0°C
Vt= Volume of a given mass of a gas at t°C
The value of v is found be 1/273 for all gases (charle's law)
Therefore, 
PRESSURE COEFFICIENT ( )
)
It is defined as the ratio of the increase in pressure of the gas at constant volume per degree rise of temperature to its pressure at 0°C
P0=Pressure of given mass of gas at 0°C
Pt=Pressure of given mass of gas at
The value found by Ragnault & Gay Lussac was in the vicinity of  for all gases and hence
for all gases and hence 
AMAGAT LAW OF PARTIAL VOLUME
The total volume of a mixture of non reacting gases at constant temperature and pressure is equal to the sum of the individual partial volumes of the constituents
V(total)= V1+V2+V3+.....+Vn 
LOSCHMIDT NUMBER
It is the number of molecules present in 1cc of a gas or vapour at STP. Its value is 2.617×1019 per cc.
AVERAGE MOLECULAR WEIGHT OF A GASEOUS MIXTURE
Mmix=
ni= number of moles
Mi= molecular weight of each component
BAROMETRIC FORMULA
The decrease in the atmospheric pressure with increase in altitude given by the following expression is called barometric formula.
ln
P0=Pressure at the sea level
P = Pressure at height h
g = acceleration due to gravity, 9.8 ms-2
R = gas constant ( 8.314 JK-1 mol-1)
T= Temperature in kelvin
ESCAPE VELOCITY
Velocity required by an object to escape from the gravitational field of a body. It is given by 
AVERAGE KINETIC ENERGY
It is KE of a single molecule,  and , where k= Boltzmann constant
and , where k= Boltzmann constant 
Total KE =N (average KE), N (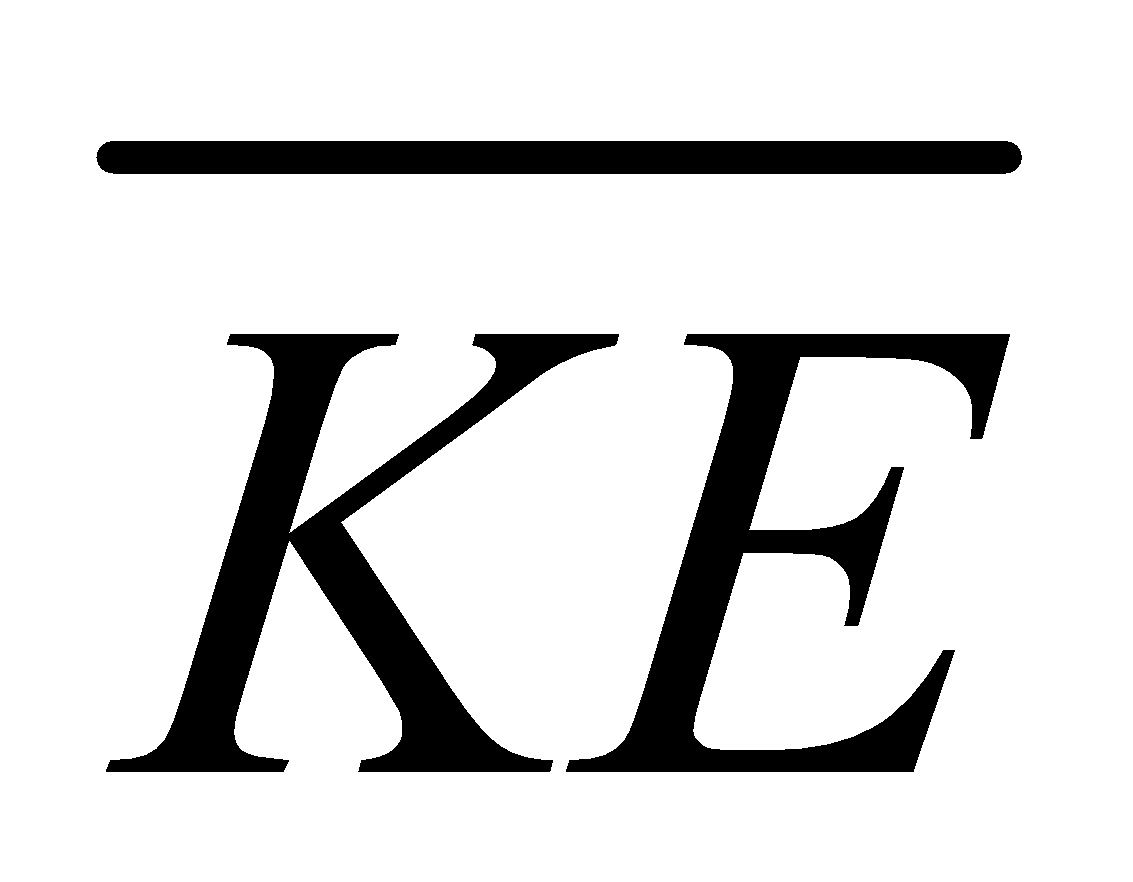 ) =
) = 
LIQUEFACTION OF GASES
Liquefaction of gas can be achieved by
- Increasing pressure : It increases attraction among molecules.
- Decreasing temperature : It decrease Kinetic energy of molecules. The temperature of gas must be lower than its critical temperature, TC.
Liquefaction is further based on the following principles
- Cooling by freezing mixture : eg NaCl & ice (-22°C), CaCl2 & ice(-55°C), KOH & ice (-65°C)
- Cooling by adiabatic expansion (Claude’s Method) : The gas in this process suffers a loss in temperature. Work is done by the gas at the cost of internal energy and temperature is lowered.
- Cooling by Joule-Thomson effect ( Linde’s method) : Expansion of a gas through a small jet under adiabatic conditions results in cooling and liquefaction of gas
LIQUID STATE
- Liquid state of the matter is the intermediate state between the gaseous and the solid state.
- In liquids the molecules of the matter are held together by strong intermolecular forces in comparison to those in gases.
- On the basis of kinetic molecular model, the liquid state is described as follow:
- A liquid is composed of small molecules.
- The molecules of the liquid are held closer by some kind of intermolecular forces.
- The intermolecular forces are not very strong and thus the molecules are always in constant random motion.
- The average kinetic energy of molecules of a liquid is directly proportional to their absolute temperature.
- Properties of the liquid :
Most of the physical properties of liquids are controlled by the strength of intermolecular attractive forces existing between molecules of a liquid. These intermolecular forces arranged in order of their increasing strength are
London forces/induced dipole<dipole attraction< Hydrogen bonding
- Shape: Liquids have no definite shape of their own. It acquires the shape of the container in which it is put.
- Volume: Liquids have a definite volume.
- Density: The densities of liquids are nearly 1000 times more than the densities of the gases under identical conditions.
- Compressibility: Liquids are very less compressible compared to gases.
- Diffusion: Liquids diffuse like gases but the process of diffusion (also known as intermixing) is much slower.
- Evaporation: The process of conversion of a liquid into its vapours (i.e.) gaseous state) at room temperature is known as evaporation.
VAPOUR PRESSURE
At equilibrium state the pressure exerted by vapour phase is called vapour pressure at a specific temperature.
- The magnitude of vapour pressure depends upon the following two factors.
- The liquids having weak intermolecular attraction have greater tendency of escaping from the liquid surface in comparison to liquids having stronger forces of intermolecular attraction. For example, the vapour pressure of ether and acetone is more than that of water or acetic acid at any specific temperature.
- The vapour pressure of a liquid increases with the increase in temperature.
- The vapour pressures of a given liquid at two different temperatures may be compared using Clausius Clapeyron equation
where P1and P2 are the vapour pressures at temperature T1 and T2 ΔH is the heat of vapourisation and R is molar gas constant.
- The temperature at which the vapour pressure of liquid becomes equal to atmospheric pressure (or the external pressure) is termed as the boiling point of liquid. For example at 1 atmospheric pressure acetone boils at 56°C. benzene at 80°C, ethyl alcohol at 78.4°C and water at 100°C.
- The temperature at which the solid state and the liquid form of a substance are in equilibrium at one atmospheric pressure is known as freezing point
SURFACE TENSION
- The surface tension is defined as the force per cm acting perpendicular to the tangential line on the surface of the liquid which tend to compress the surface area.
- The units of surface tension are force per unit length i.e. dynes cm–1 or Nm–1 (in SI units)
- Stronger the forces of intermolecular attraction (cohesive forces) greater is the surface tension.
- The surface tension decreases with rise in temperature or surface tension in inversely proportional to temperature.Surface tension
1/Temperature
- Measurement of surface tension of a liquid by the drop number method is the most convenient method.
VISCOSITY
- Viscosity may be defined as the force of friction between two layers of a liquid moving past one another with different velocities.
- The viscosities of liquids are compared in terms of coefficient of viscosity which is defined as the force per unit area needed to maintain a unit difference in velocities between two consecutive parallel layers which are one cm. apart.
- The units of viscosity are poise (P) where 1P = g cm–1 sec–1. In SI units of viscosity 1P = 0.1 N sec m–2.
- The liquid having stronger forces of attraction has a higher viscosity.
- With the rise in temperature, viscosity of a liquid decreases because the intermolecular attractive force between consecutive layers decrease as temperature increases.










