WORK, POWER AND ENERGY
WORK
WORK DONE BY A CONSTANT FORCE
Work done (W) by a force 
in displacing a body through a displacement x is given by
in displacing a body through a displacement x is given by 
= Fx cos θ
Where θ is the angle between the applied force and displacement
.
and displacement.
The S.I. unit of work is joule, CGS unit is erg and its dimensions are [ML2T–2].
1 joule = 107 erg
- When θ = 0° then W = Fx
- When θ is between 0 and π/2 then
W = Fx cos θ = positive
- When θ = Ï€/2 then W = Fx cos 90° = 0 (zero)
Work done by centripetal force is zero as in this case angle θ = 90°
- ∴ When θ is between Ï€/2 and Ï€ then
W = Fx cos θ = negative
WORK DONE BY A VARIABLE FORCE
When the force is an arbitrary function of position, we need the techniques of calculus to evaluate the work done by it. The figure shows Fx as function of the position x. We begin by replacing the actual variation of the force by a series of small steps.
The area under each segment of the curve is approximately equal to the area of a rectangle. The height of the rectangle is a constant value of force, and its width is a small displacement Δx. Thus, the step involves an amount of work ΔWn = Fn Δxn. The total work done is approximately given by the sum of the areas of the rectangles.
i.e., W ≈ 
Δxn.
Δxn. 
As the size of the steps is reduced, the tops of the rectangle more closely trace the actual curve shown in figure. If the limit Δx → 0, which is equivalent to letting the number of steps tend to infinity, the discrete sum is replaced by a continuous integral.
Thus, the work done by a force Fx from an initial point A to final point B is
The work done by a variable force in displacing a particle from x1 to x2
= area under force displacement graph
CAUTION : When we find work, we should be cautious about the question, work done by which force? Let us take an example to understand this point. Suppose you are moving a body up without acceleration.
Work done by applied force
Work done by gravitational force
ENERGY
It is the capacity of doing work. Its units and dimensions are same as that of work.
POTENTIAL ENERGY
The energy possessed by a body by virtue of its position or configuration is called potential energy. Potential energy is defined only for conservative forces. It does not exist for non-conservative forces.
ELASTIC POTENTIAL ENERGY (POTENTIAL ENERGY OF A SPRING)
Let us consider a spring, its one end is attached to a rigid wall and other is fixed to a mass m. We apply an external force 
on mass m in the left direction, so that the spring is compressed by a distance x.
on mass m in the left direction, so that the spring is compressed by a distance x.
If spring constant is k, then energy stored in spring is given by
P.E. of compressed spring = ½kx2
Now if the external force is removed, the mass m is free to move then due to the stored energy in the spring, it starts oscillating
GRAVITATIONAL POTENTIAL ENERGY
When a body is raised to some height, above the ground, it acquires some potential energy, due to its position. The potential energy due to height is called gravitational potential energy. Let us consider a ball B, which is raised by a height h from the ground.
In doing so, we do work against gravity and this work is stored in the ball B in the form of gravitational potential energy and is given by
W = Fapp.h = mgh = gravitational potential energy ...(i)
Further if ball B has gravitational P.E. (potential energy) Uo at ground and at height h, Uh, then
Uh–Uo =mgh ...(ii)
If we choose Uo= 0 at ground (called reference point) then absolute gravitational P.E of ball at height h is
Uh = mgh ...(iii)
In general, if two bodies of masses m1 and m2 are separated by a distance r, then the gravitational potential energy is
KINETIC ENERGY
The energy possessed by a body by virtue of its motion is called kinetic energy.
The kinetic energy Ek is given by
Ek = ½ mv2 ...(i)
Where m is mass of body, which is moving with velocity v. We know that linear momentum (p) of a body which is moving with a velocity v is given by
p = mv ...(ii)
So from eqs. (i) and (ii), we have
...(iii)
This is the relation between momentum and kinetic energy.
The graph between 
and p is a straight line
and p is a straight line 
The graph between 
and 
is a rectangular hyperbola
and is a rectangular hyperbola
The graph between Ek and 
is a rectangular hyperbola
is a rectangular hyperbola
KEEP IN MEMORY
- Work done by the conservative force in moving a body in a closed loop is zero.
Work done by the non-conservative force in moving a body in a closed loop is non-zero.
- If the momenta of two bodies are equal then the kinetic energy of lighter body will be more.
- If the kinetic energies of two bodies are same then the momentum of heavier body will be more.
WORK-ENERGY THEOREM
Let a number of forces acting on a body of mass m have a resultant force 
and by acting over a displacement x (in the direction of 
), 
does work on the body, and there by changing its velocity from u (initial velocity) to v (final velocity). Kinetic energy of the body changes.
and by acting over a displacement x (in the direction of ), does work on the body, and there by changing its velocity from u (initial velocity) to v (final velocity). Kinetic energy of the body changes.
So, work done by force on the body is equal to the change in kinetic energy of the body.
This expression is called Work energy (W.E.) theorem.
LAW OF CONSERVATION OF MECHANICAL ENERGY
The sum of the potential energy and the kinetic energy is called the total mechanical energy.
The total mechanical energy of a system remains constant if only conservative forces are acting on a system of particles and the work done by all other forces is zero.
i.e., ΔK + ΔU = 0
or Kf – Ki + Uf – Ui = 0
or Kf + Uf = Ki + Ui = constant
LAW OF CONSERVATION OF ENERGY
Energy is of many types – mechanical energy, sound energy, heat energy, light energy, chemical energy, atomic energy, nuclear energy etc.
In many processes that occur in nature energy may be transformed from one form to other. Mass can also be transformed into energy and vice-versa. This is according to Einstein’s mass-energy equivalence relation, E = mc2.
In dynamics, we are mainly concerned with purely mechanical energy.
The study of the various forms of energy and of transformation of one kind of energy into another has led to the statement of a very important principle, known as the law of conservation of energy.
"Energy cannot be created or destroyed, it may only be transformed from one form into another. As such the total amount of energy never changes".
KEEP IN MEMORY
- Work done against friction on horizontal surface = μ mgx and work done against force of friction on inclined plane = (μmg cosθ) x where μ = coefficient of friction.
- If a body moving with velocity v comes to rest after covering a distance ‘x’ on a rough surface having coefficient of friction μ, then (from work energy theorem), 2μ gx = v2. Here retardation is
- Work done by a centripetal force is always zero.
- Potential energy of a system decreases when a conservative force does work on it.
- If the speed of a vehicle is increased by n times, then its stopping distance becomes n2 times and if momentum is increased by n times then its kinetic energy increases by n2 times.
- Stopping distance of the vehicle
- Two vehicles of masses M1 and M2 are moving with velocities u1 and u2 respectively. When they are stopped by the same force, their stopping distance are in the ratio as follows :
Since the retarding force F is same in stopping both the vehicles. Let x1 and x2 are the stopping distances of vehicles of masses M1 & M2 respectively, then
....(i)
where u1 and u2 are initial velocity of mass M1 & M2 respectively & final velocity of both mass is zero.
....(ii)
Let us apply a retarding force F on M1 & M2, a1 & a2 are the decelerations of M1 & M2 respectively. Then from third equation of motion
:
:
....(iii a)
and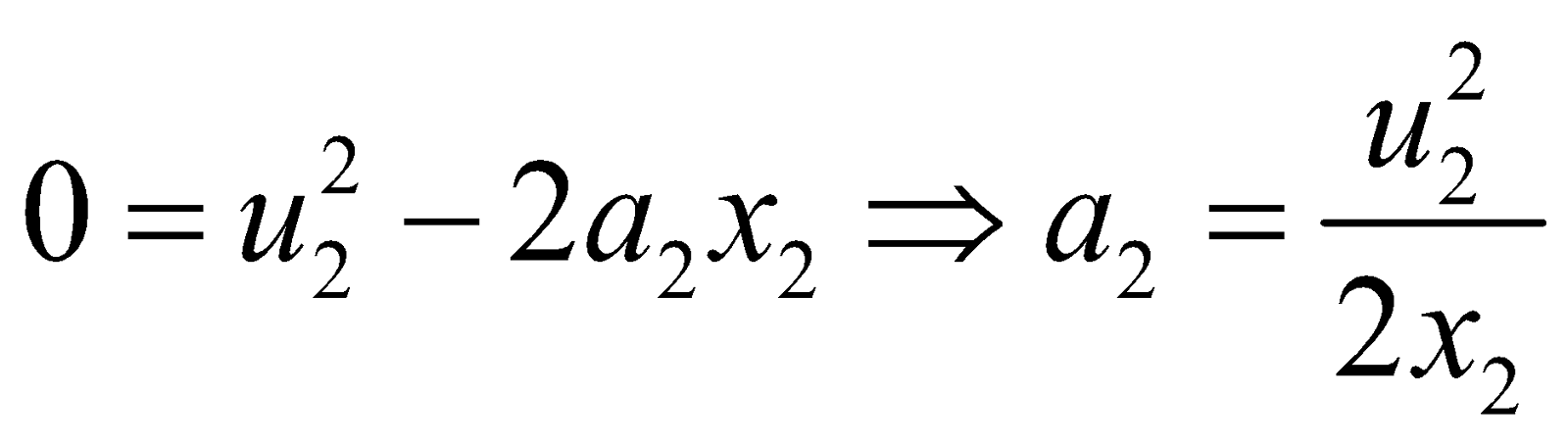 
....(iii b )
....(iii b )
If t1 & t2 are the stopping time of vehicles of masses
M1 & M2 respectively, then from first equation of motion (v = u+at)
M1 & M2 respectively, then from first equation of motion (v = u+at)
....(iv a)
and 
....(iv b)
....(iv b)
Then by rearranging equation (i), (iii) & (iv), we get
- If
- If
- If M1u1 = M2u1 ⇒ t1 = t2 and
- Consider two vehicles of masses M1 & M2 respectively.
If they are moving with same velocities, then the ratio of their stopping distances by the application of same retarding force is given by
and let M2 > M1 then x1 < x2
lighter mass will cover less distance then the heavier mass
And the ratio of their retarding times are as follows :
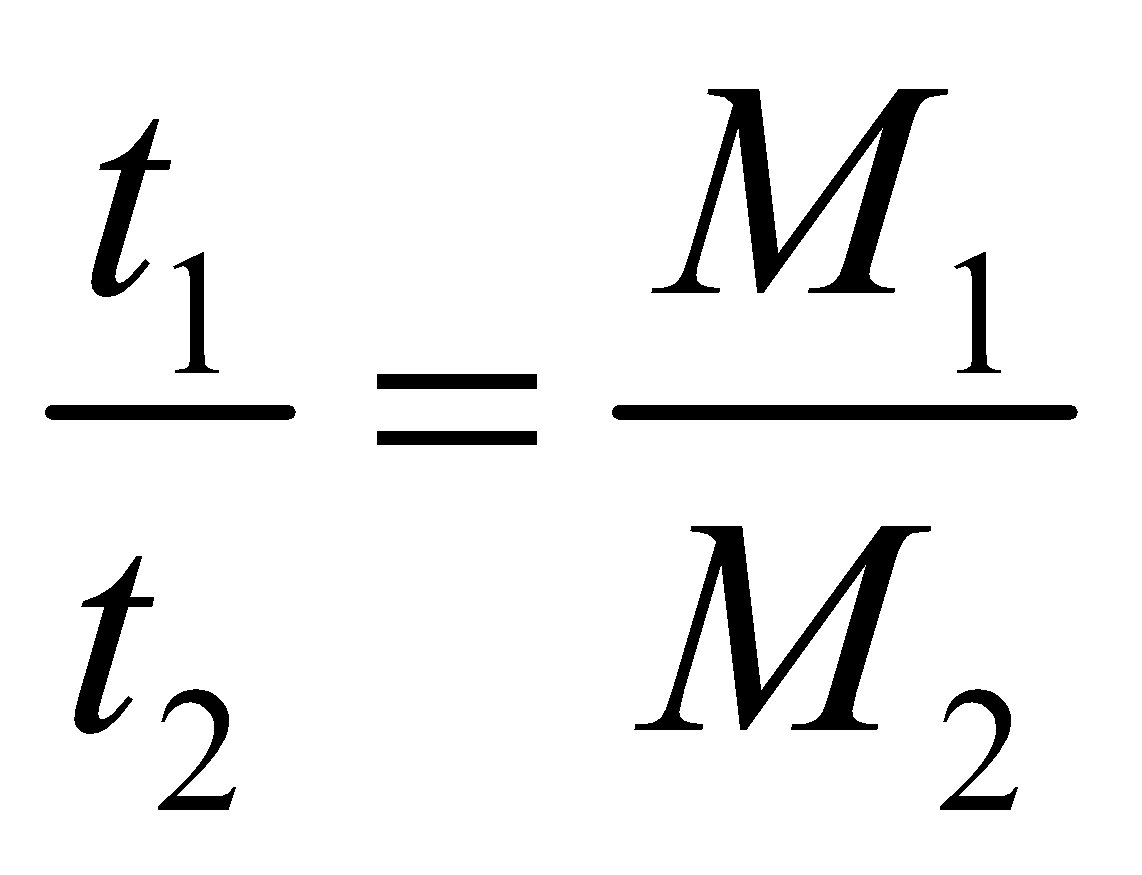i.e 
i.e - If kinetic energy of a body is doubled, then its momentum becomes
times,
- If two bodies of masses m1 and m2 have equal kinetic energies, then their velocities are inversely proportional to the square root of the respective masses. i.e.
- The spring constant of a spring is inversely proportional to the no. of turns i.e.
or kn = const.
Greater the no. of turns in a spring, greater will be the work done i.e. W ∝ n
The greater is the elasticity of the spring, the greater is the spring constant.
- Spring constant : The spring constant of a spring is inversely proportional to length i.e.,
or Kl = constant.
- If a spring is divided into n equal parts, the spring constant of each part = nK.
- If spring of spring constant K1, K2, K3 .......... are connected in series, then effective force constant
- If spring of spring constant K1, K2, K3........... are connected in parallel, then effective spring constant
Keff = K1 + K2 + K3 +.............
POWER
Power of the body is defined as the time rate of doing work by the body.
The average power Pav over the time interval Δt is defined by
...(i)
And the instantaneous power P is defined by
...(ii)
Power is a scalar quantity
The S.I. unit of power is joule per second
1 joule/sec = 1watt
The dimensions of power are [ML2T–3]
(force is constant over a small time interval)
So instantaneous power (or instantaneous rate of working) of a man depends not only on the force applied to body, but also on the instantaneous velocity of the body.
COLLISION
Collision between two bodies is said to take place if either of two bodies come in physical contact with each other or even when path of one body is affected by the force exerted due to the other.
- Elastic collision : The collision in which both the momentum and kinetic energy of the system remains conserved is called elastic collision.
Forces involved in the interaction of elastic collision are conservative in nature.
- Inelastic collision : The collision in which only the momentum of the system is conserved but kinetic energy is not conserved is called inelastic collision.
Perfectly inelastic collision is one in which the two bodies stick together after the collision.
Forces involved in the interaction of inelastic collision are non-conservative in nature.
COEFFICIENT OF RESTITUTION (OR COEFFICIENT OF RESILIENCE)
It is the ratio of velocity of separation after collision to the velocity of approach before collision. i.e., e = | v1 – v2 |/ | u1 – u2 |
Here u1 and u2 are the velocities of two bodies before collision and v1 and v2 are the velocities of two bodies after collision.
- 0 < e < 1 (Inelastic collision)
Collision between two ivory balls, steel balls or quartz ball is nearly elastic collision.
- For perfectly elastic collision, e = 1
- For a perfectly inelastic collision, e = 0
OBLIQUE ELASTIC COLLISION
When a body of mass m collides obliquely against a stationary body of same mass then after the collision the angle between these two bodies is always 90°.
ELASTIC COLLISION IN ONE DIMENSION (HEAD ON)
Let two bodies of masses M1 and M2 moving with velocities u1 and u2 along the same straight line, collide with each other. Let u1>u2. Suppose v1 and v2 respectively are the velocities after the elastic collision, then:
According to law of conservation of momentum
...(1)
From law of conservation of energy
...(2)
...(3)
Relative velocity of a Relative velocity of a
body before collision body after collision
Solving eqs. (1) and (2) we get,
...(4) 
...(5)
From eqns. (4) and (5), it is clear that :
- If M1 = M2 and u2 = 0 then v1 = 0 and v2 = u1. Under this condition the first particle comes to rest and the second particle moves with the velocity of first particle after collision. In this state there occurs maximum transfer of energy.
- If M1>> M2 and (u2=0) then, v1 = u1, v2 = 2u1 under this condition the velocity of first particle remains unchanged and velocity of second particle becomes double that of first.
- If M1 << M2 and (u2 = 0) then v1 = –u1 and v2 =
0 under this condition the second particle remains at rest while the first particle moves with the same velocity in the opposite direction.
- If M1 = M2 = M but u2 ≠0 then v1 = u2 i.e., the particles mutually exchange their velocities.
- If second body is at rest i.e., u2 = 0, then fractional decrease in kinetic energy of mass M1, is given by
INELASTIC COLLISION
Let two bodies A and B collide inelastically. Then from law of conservation of linear momentum
M1u1 + M2u2 = M1v1+M2v2 ...(i)
e 
...(ii)
...(ii)
From eqns.(i) and (ii), we have,
...(iii)
...(iv)
Loss in kinetic energy (–ΔEk) = initial K.E. – final K.E
⇒ 
⇒ 
...(v)
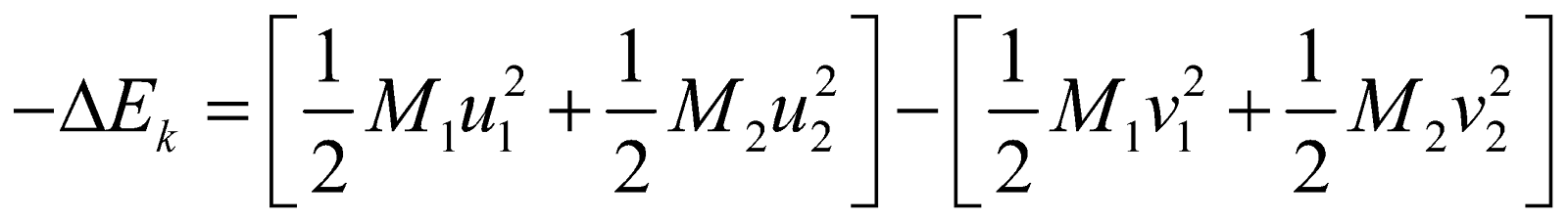
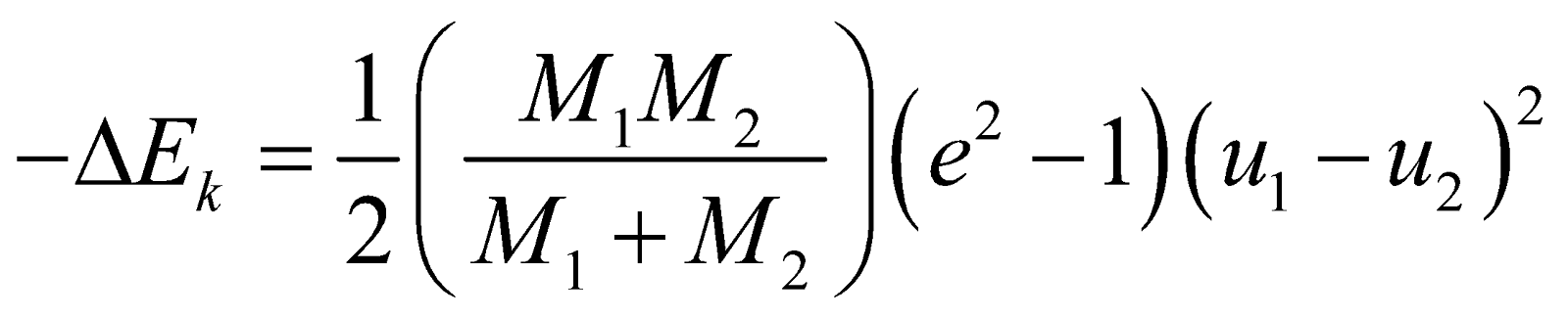...(v)
Negative sign indicates that the final kinetic energy is less than initial kinetic energy.
PERFECTLY INELASTIC COLLISION
In this collision, the individual bodies A and B move with velocities u1 and u2 but after collision move as a one single body with velocity v.
So from law of conservation of linear momentum, we have
M1u1+M2u2=(M1+M2)V ...(i)
or 
...(ii)
...(ii)
And loss in kinetic energy, –ΔEk = total initial K.E – total final K.E
or,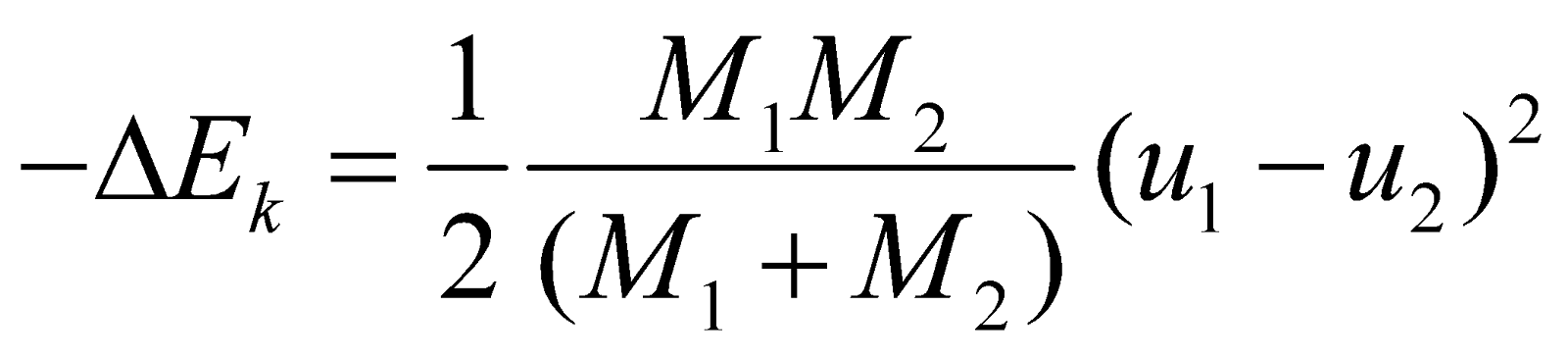 
...(iii)
...(iii)OBLIQUE COLLISION
This is the case of collision in two dimensions. After the collision, the particles move at different angle.
We will apply the principle of conservation of momentum in the mutually perpendicular direction.
Along x-axis, m1u1 = m1v1 cosθ + m2 v2 cosφ
Along y-axis, 0 = m1v1 sinθ - m2 v2 sinφ
KEEP IN MEMORY
- Suppose, a body is dropped from a height h0 and it strikes the ground with velocity v0. After the (inelastic) collision let it rise to a height h1. If v1 be the velocity with which the body rebounds, then the coefficient of restitution.
= 
- If after n collisions with the ground, the velocity is vn and the height to which it rises be hn, then
- When a ball is dropped from a height h on the ground, then after striking the ground n times , it rises to a height hn = e2n ho where e = coefficient of restitution.
- If a body of mass m moving with velocity v, collides elastically with a rigid ball, then the change in the momentum of the body is 2 m v.
- If the collision is elastic then we can conserve the energy as
- If two particles having same mass and moving at right angles to each other collide elastically then after the collision they also move at right angles to each other.
- If a body A collides elastically with another body of same mass at rest obliquely, then after the collision the two bodies move at right angles to each other, i.e. (θ + φ) =
- In an elastic collision of two equal masses, their kinetic energies are exchanged.
- When two bodies collide obliquely, their relative velocity resolved along their common normal after impact is in constant ratio to their relative velocity before impact (resolved along common normal), and is in the opposite direction.
Study Notes for JEE Main/JEE Advanced
Study Notes for NEET/AIIMS
