Dual Nature of Radiation and Matter | Physics Notes for IITJEE/NEET

DUAL NATURE OF RADIATION AND MATTER

CATHODE RAYS

DISCHARGE TUBE EXPERIMENTS

When a very strong potential difference is applied across the two electrodes in a discharge tube and the pressure of the air is lowered gradually, then a stage is reached at which the current begins to flow through the air with cracking noise. The potential at which this happens is called sparking potential.

• As pressure is lowered to 0.1 mm. Hg – cathode glow, Crooke’s dark space, negative glow, Faraday’s dark space and striations are observed.
• At a pressure 0.01 mm. Hg entire tube is dark (Crooke’s dark space) except the glass wall behind anode. Colour is yellowish-green for soda glass and greyish-blue for lead glass.
• The luminous streaks travelling from cathode to anode, below the pressure 0.01 mm. Hg, are called cathode rays.

PROPERTIES OF CATHODE RAY

• Emitted perpendicularly to cathode,
• Travel in straight lines
• Carry energy
• Possesses momentum
• Deflected by electric and magnetic fields
• Excite fluorescence
• Ionise gas
• Produce highly penetrating secondary radiation when suddenly stopped
• Effect photographic plate

J.J. THOMSON’S E/M VALUE OF ELECTRON

This value of 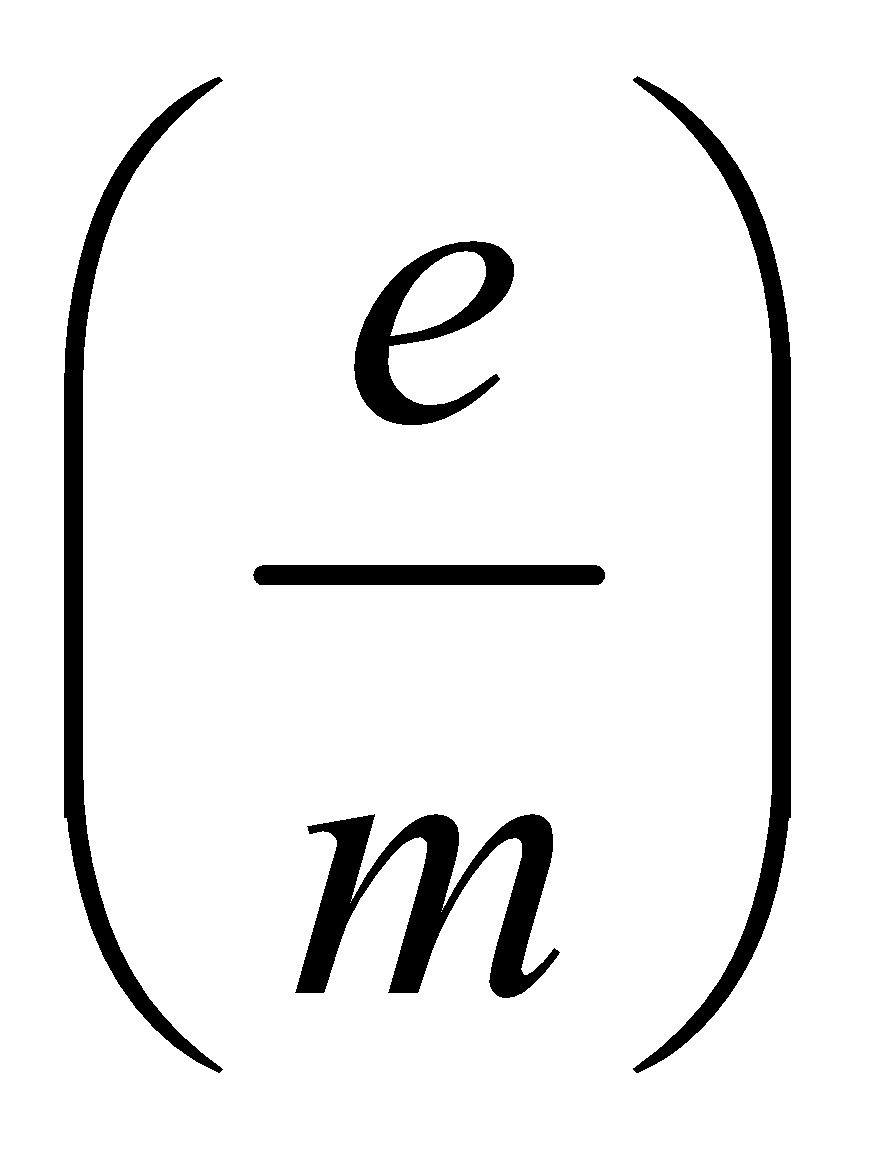is for electron.

MILLIKAN’S OIL DROP METHOD FOR E/M

In fig.(a) we consider a single drop of mass m carrying a negative charge –q in the absence of electric field. Then

Fviscous 1 = mg   [from Stoke’s law Fviscous = 6πηrv]

or   6π rv1 = mg …(1)

where 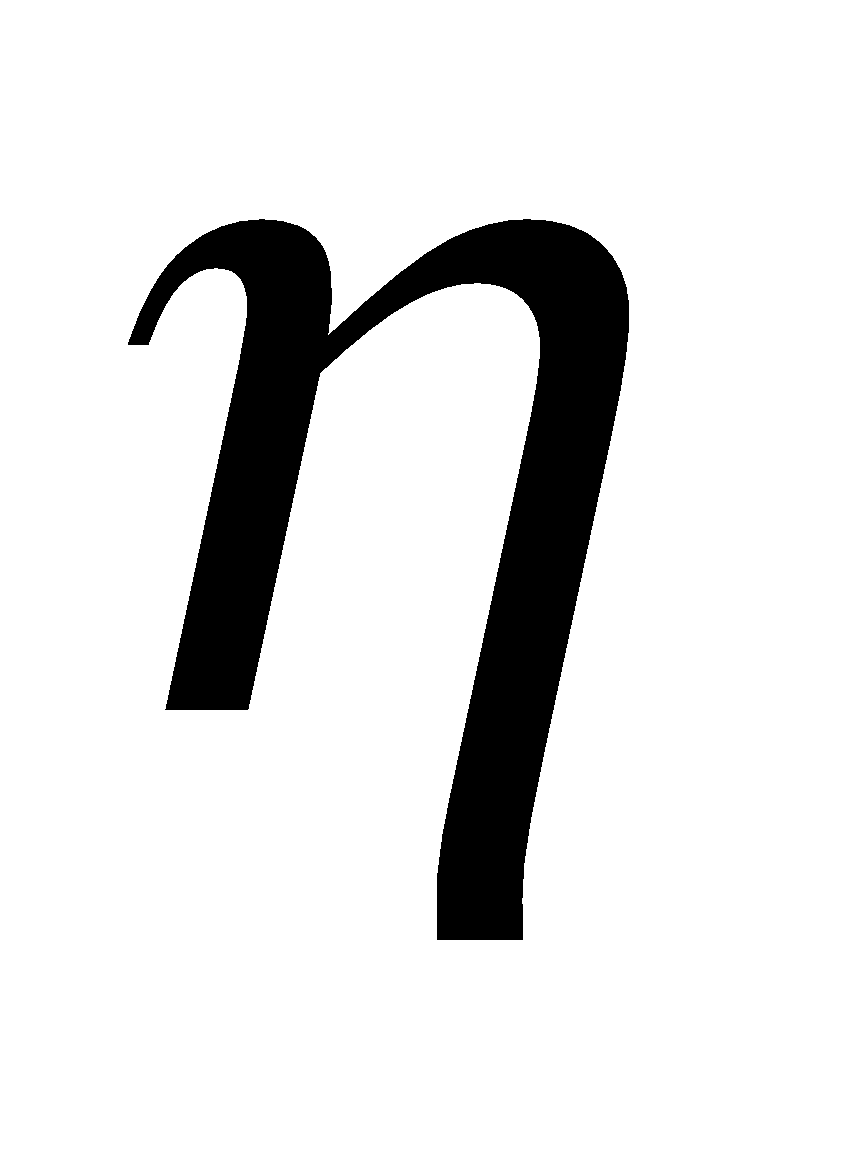is coefficient of viscosity of air, r is radius of drop  and v1 is the terminal velocity of drop.

In fig. (b) we consider a single drop of mass m, radius r carrying a negative charge –q in the presence of electric field acting downward. Then by free body diagram (fig. (b)), we get

…(2)

where v2 is the terminal speed in this case. Then from eqn (1), we have.

…(3)

and radius of drop from equation (1)

or …(4)

where ρ is density of drop.

Millikan repeated these measurements on thousands of drops and he found that the charge q calculated for each drop was some integral multiple of an elementary charge e. (e = 1.6 × 10–19C).

Hence, q = ne,   n = 0, ±1, ±2 ...(5)

This experiment gives the evidence of quantisation of charge.

EMISSION OF ELECTRON

Electrons from the metal surface are emitted by anyone of the following physical processes :

• Thermionic emission : The emission of electrons by suitably heating  the metal surface.
• Field emission : The emission of electrons by applying very  strong field of the order of 108 Vm–1 to a metal.
• Photoelectric emission : The emission of electrons when light of suitable frequency illuminates metal surface.

PHOTOELECTRIC EFFECT (EINSTEIN’S PHOTOELECTRIC EQUATION)

In 19th century, experiments showed that when light is incident on certain metallic surfaces, electrons are emitted from the surfaces. This phenomenon is known as the photoelectric effect & emitted electrons are called photoelectrons. The first discovery of this phenomenon was made by Hertz.

When light strikes the cathode C (metallic surface), photo electrons are ejected. Electrons are collected at anode A, constituting a current in the circuit. (Photoelectric effect)

Fig. shows, when light strikes the cathode C, electrons are emitted & they are collected on anode A due to potential difference provided by battery and constitutes the current in the circuit (observed by Galvanometer G.)

A plot of photoelectric current versus the potential difference V between cathode & anode is shown in fig below.

Photoelectric current versus voltage for two light intensities.
At a voltage less than –V0 the current is zero.

It is clear from fig. that photoelectric current increases as we increase the intensity of light & obtain saturation value at larger value of potential difference V between cathode & anode. If V is negative then, photoelectrons are repelled by negative cathode and only those electrons reaches anode, who have energy equal to or greater than eV. But if V is equal to V0, called stopping potential (i.e., cut off. potential), no electrons will reach the anode

i.e., Maximum kinetic energy of electron = eV0

or Kmax = eV0 ...(1)

where e is charge of electron (e = 1.6 × 10–19 coulomb).

But some features of photoelectric effect cannot be explained by classical physics & the wave theory of light.

• No photoelectrons are emitted, if the frequency of incident light is less than some cut-off frequency (i.e., threshold frequency) ν0. It is inconsistent with the wave theory of light, which predicts that photoelectric effect occurs at any frequency provided intensity of incident light is sufficiently high.
• The maximum kinetic energy of the photoelectrons is independent of light intensity, but increases with increasing the frequency of incident light.
• Electrons are emitted from surface almost instantaneously (less than 10–9 sec after the surface illumination), even at low intensity of incident light (classically we assume that the electrons would require some time to absorb the incident light before they acquire enough kinetic energy to escape from metal).

These above points were explained by Einstein in 1905 by treating the light as stream of particles.

Taking Max Planck assumptions, Einstein postulated that a beam of light consists of small packets of energy called photons or quanta. The energy E of a photon is equal to a constant h times its frequency ν

i.e., ...(2)

where h is a universal constant called Planck’s constant & numerical value of  h = 6.62607 × 10–34 J.s

When a photon arrives at surface, it is absorbed by an electron. This energy transfer is an All-or-None process, in contrast to continuous transfer of energy in classical theory; the electrons get all photon’s energy or none at all. If this energy is greater than the work function (φ) of the metal (φ is the minimum energy required to remove the electron from metal surface), the electron may escape from the surface. Greater intensity at a particular frequency means greater number of photons per second absorbed & consequently greater number of electrons emitted per second & so greater current.

To obtain maximum kinetic energy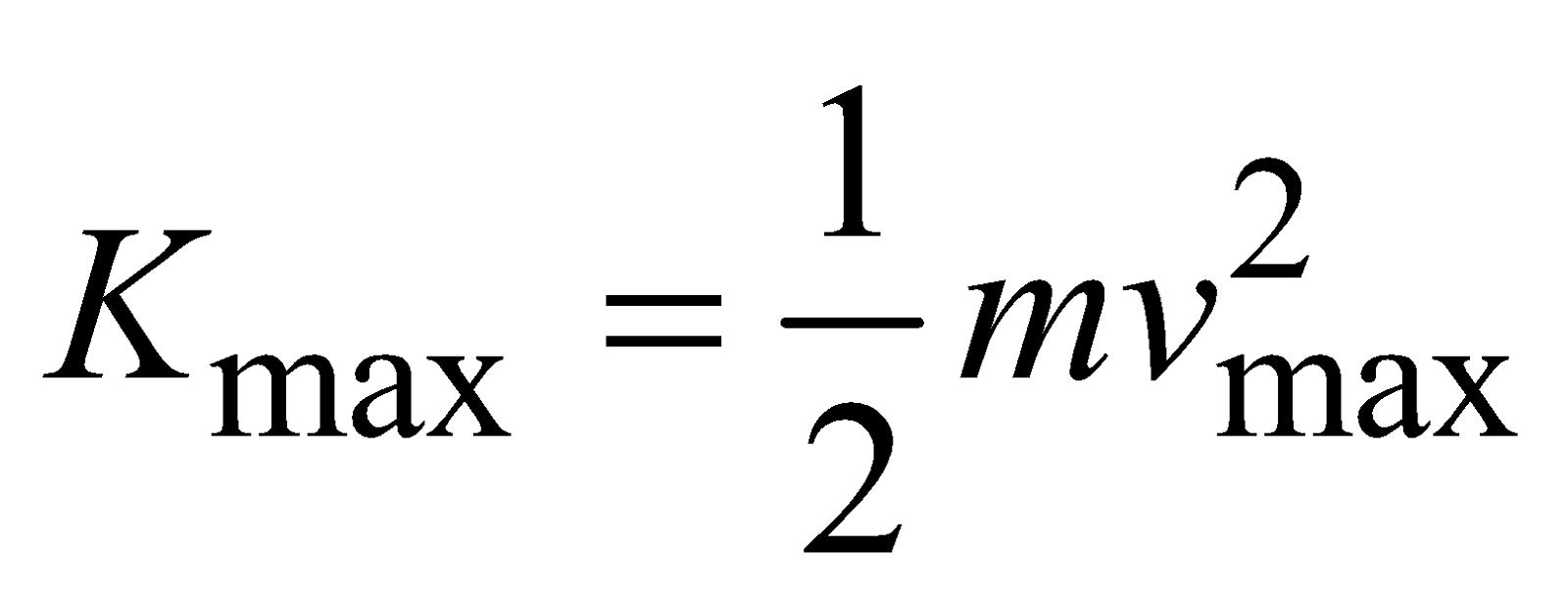  

for an emitted electron, applying law of conservation of energy.

According to it

               

               ...(3)

or       ...(4)

or,

This is the Einstein’s photoelectric equation.

where   V0 = cut-off potential

            νmax = maximum velocity obtained by photoelectrons

            ν = frequency of incident light i.e., photon

            ν0 = cut off frequency or threshold frequency.

ν0 is different for different metallic surfaces. For most metals the threshold frequency is in ultraviolet region of spectrum. (Corresponding to λ between 200 & 300 nm), but for potassium & cesium oxides, it is in the visible spectrum (λ between 400 & 700 nm).

Work Function (φ) of Some Elements Given in Brackets :

Al (4.3eV) Ni   (5.1 eV)

C (5.0 eV) Si   (4.8 eV)

Cu (4.7 eV) Ag   (4.3 eV)

Au (5.1eV) Na (2.7 eV)

where 1 eV = 1.602 × 10–19 joule.

Within the framework of photon theory of light (Quantum theory of light) we can explain above failures of classical physics.

• It is clear from eq. (3) that if energy of photon is less than the work function of metallic surface, the electrons will never be ejected from the surface regardless of intensity of incident light.
• Kmax is independent of intensity of incident light, but it depends on the frequency of incident light i.e., Kmax ∝ ν (frequency of light).
• Electrons are emitted almost instantaneously consistent with particle view of light in which incident energy is concentrated in small packets (called photons) rather than over a large area (as in wave theory).

VARIOUS GRAPHS RELATED TO PHOTOELECTRIC EFFECT

Photocurrent versus intensity of light graph

Photocurrent versus potential graph

Maximum kinetic energy versus potential graph

KEEP IN MEMORY

1. Mass spectrograph is an apparatus used to determine the mass or the specific charge (e/m) of positive ions. Examples are (a) Thomson mass spectrograph (b) Bain bridge mass spectrograph (c) Aston mass spectrograph (d) Dempster mass spectrograph etc.
2. In photoelectric effect all photoelectrons do not have same kinetic energy. Their KE ranges from zero to Emax which depends on frequency of incident radiation and nature of cathode.
3. The photoelectric effect takes place only when photons strike bound electrons because for free electrons energy and momentum conservations do not hold together.
4. Cesium is the best photo sensitive material.
5. Efficiency of photoemission

Therefore,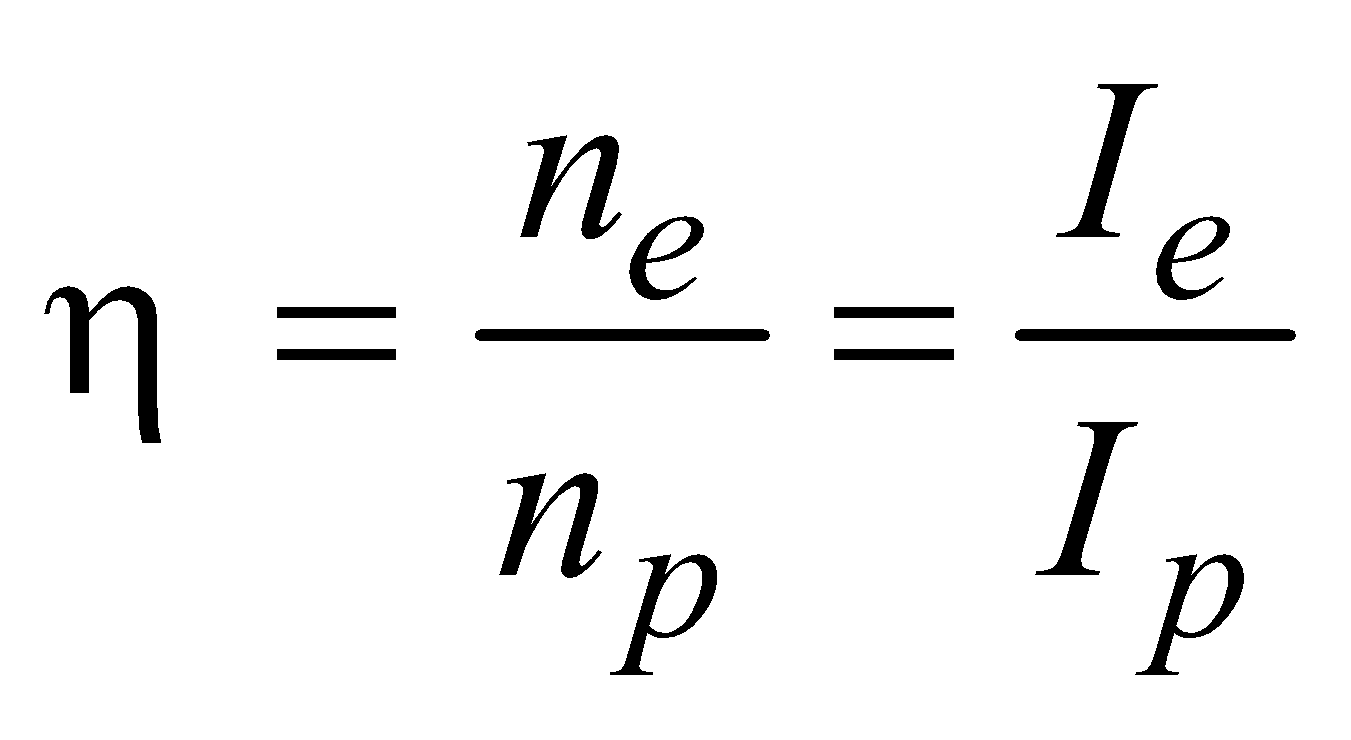  

6. Maximum velocity of emitted electrons

7. Stopping potential

DE-BROGLIE EQUATION (DUAL NATURE OF MATTER)

In 1924, Louis de Broglie, wrote a doctoral dissertation in which he proposed that since photons have wave and particle characteristics, perhaps all forms of matter have wave as well as particle properties.

This is called dual nature of matter.  According to which a matter particle moving with a velocity v can be treated as a wave of wavelength λ. This λ is called de-Broglie wavelength & it is defined as :

...(1)

where m is the mass of matter particle & these waves are called matter waves.

Further with the analogy of photon, the frequency of matter waves is

...(2)

The dual nature of matter is quite apparent in these two equations (equations (1) & (2)). i.e.,  each equation contains both particle concepts (mv & E) & wave concepts (λ & ν). It is clear from next topic that Compton effect confirm the validity of p = h/λ for photons, and the photoelectric effect confirms the validity and E = hν for photons.

de-Broglie wavelength associated with electron accelerated under a potential difference V volt is given by

de-Broglie wave is not an electromagnetic wave but the matter wave.

WAVELENGTH OF MATTER WAVES ASSOCIATED WITH ACCELERATED CHARGED PARTICLES

If V is the accelerating voltage applied then :

• For the charged particle

Energy E = qV ;

Velocity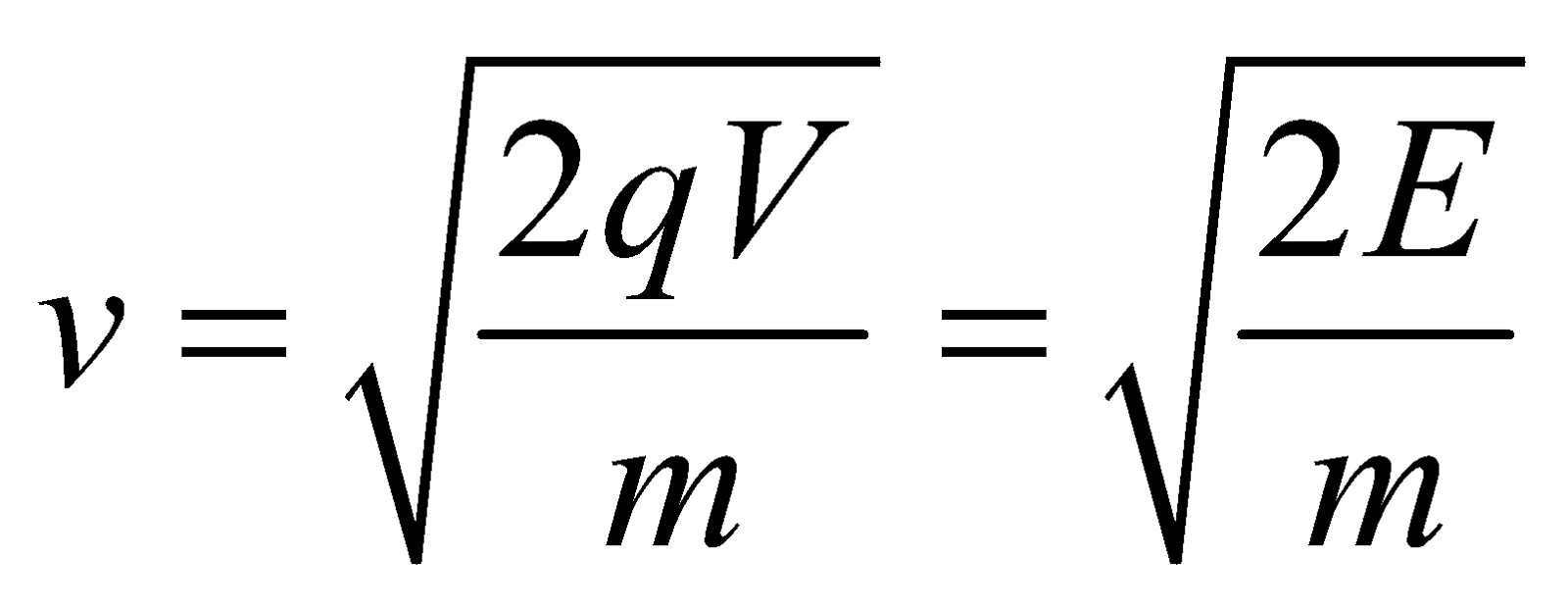

Momentum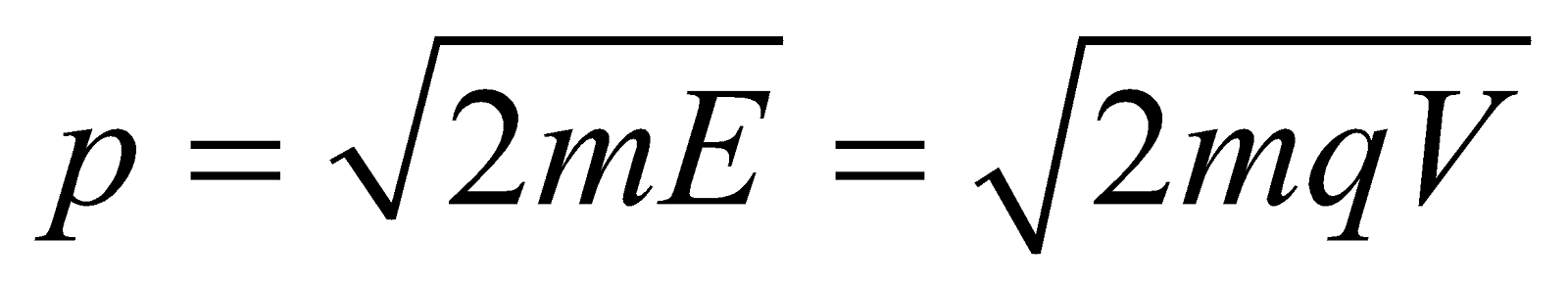  

Wavelength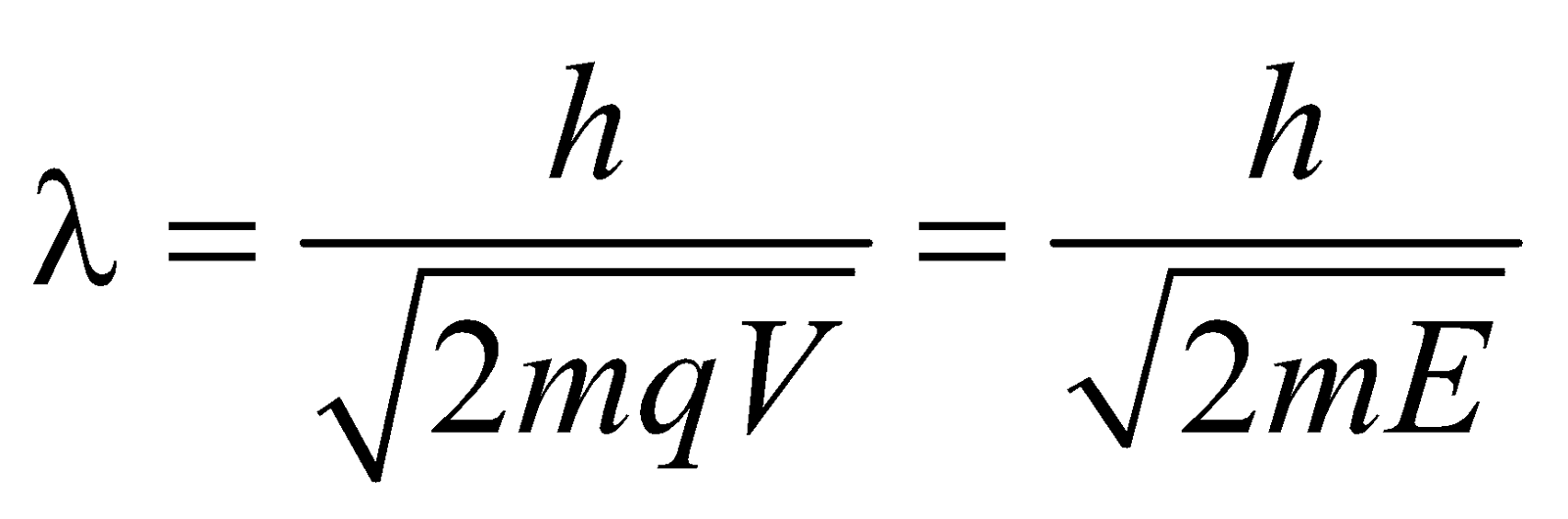  

• For electron λe = Å
• For proton λp = Å
• For alpha particle λα = Å
• For deuteron λd = Å
• For neutral particles (neutron, atom or molecule)
• If E is the energy of the particle, then,
• If T is the temperature, then,

DAVISSON-GERMER EXPERIMENT

Idea of de-Broglie wave was tested beautifully in 1926 in an experiment performed by C. Davisson (1881-1958) and L.H. Germer (1896-1971). They directed a beam of electrons at a crystal and observed that the electrons scattered in various directions for a given crystal orientation.

In this experiment the pattern formed by the electrons reflected from the crystal lattice of aluminium is almost identical to that produced by X-rays. This strongly suggests that the electrons have a wavelength λ associated with them and that the Bragg condition for X-ray diffraction holds true for electron also :

BRAGG’S EQUATION

nλ = D sin θ or nλ = 2d sin φ.

Diffraction maximum of electrons accelerated with 54 volt is obtained at θ = 50º for the Nickel crystal.

EXPLANATION OF BOHR’S QUANTUM CONDITION

• According to Bohr’s quantum conditions :

Angular momentum,

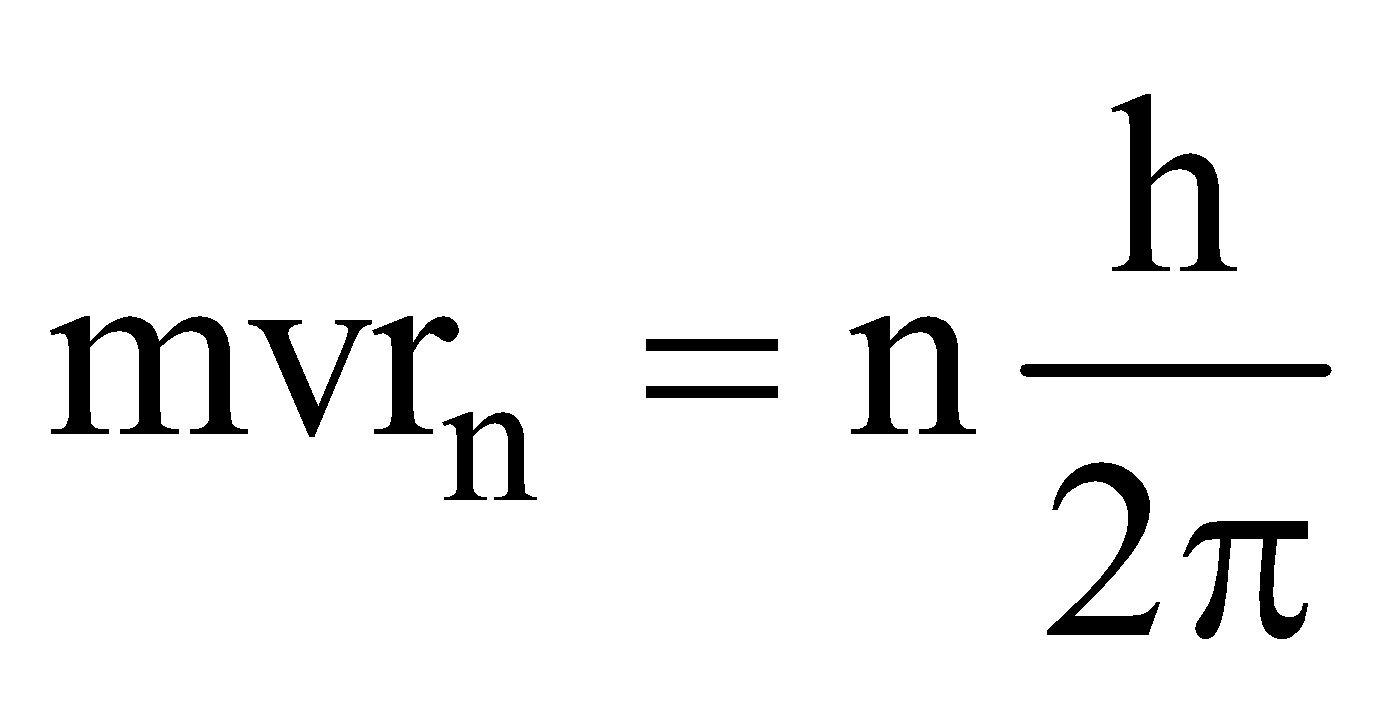
• Matter waves associated with the electrons moving in an orbit are stationary waves.
• For the production of stationary waves in the orbit the circumference of the orbit should be integral multiple of wavelength of waves associated with the electron,

i.e.,  2πrn = nλ, where   

∴

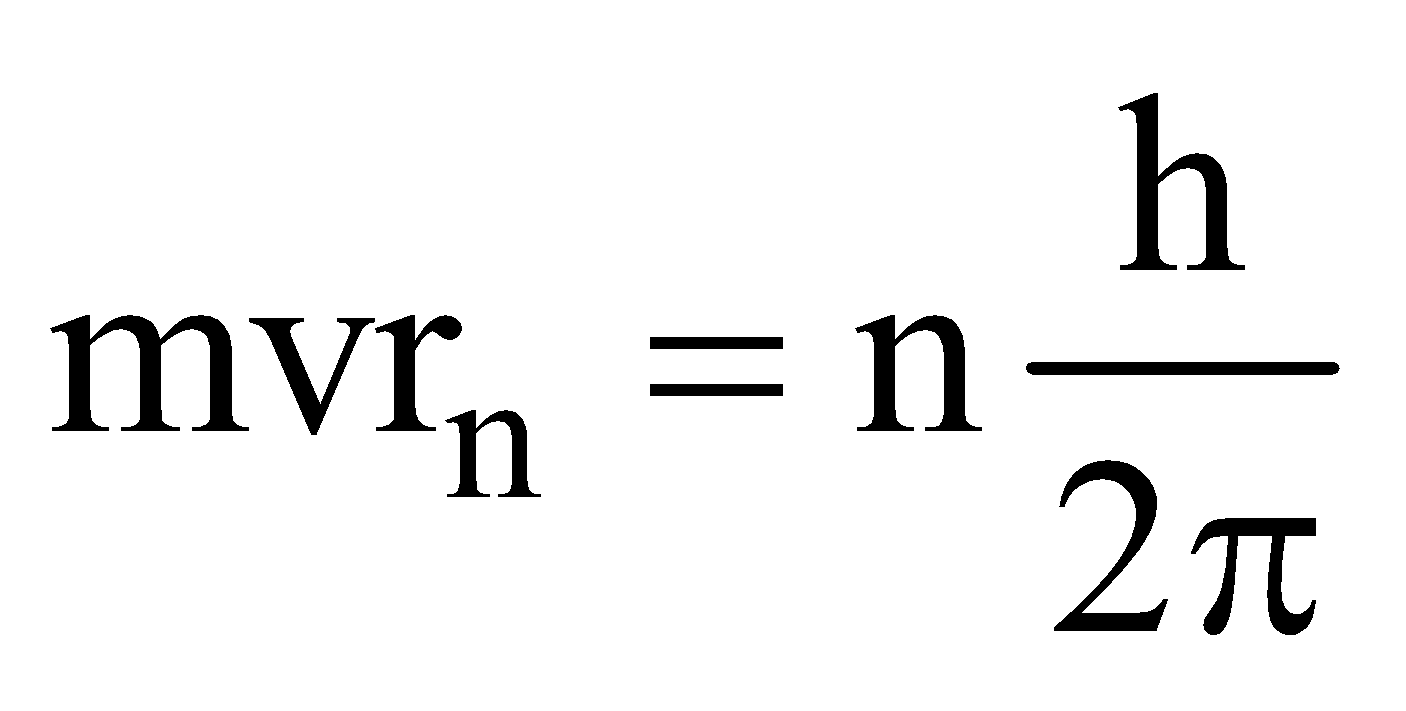
COMPTON EFFECT

Further experimental proof for photon concept (i.e., particle nature of light) was discovered in 1923 by American Physicist, A.H. Compton. According to which, when a monochromatic beam of X-rays (wavelength λ0) strikes the electron in a carbon target, two types of X-rays are scattered. The first type of scattered wave has same wavelength (λ0) as the incoming X-rays, while second type has a longer wavelength (λ) than incident rays (First type of X-rays are called unmodified x-rays, while second type of X-rays are called modified X-rays.) This change in wavelength i.e. Δλ = λ –  λ0 is called Compton shift & this effect is called Compton effect.

Diagram shows Compton scattering of an x-rays by free electron in a carbon target. The scattered x-rays has less energy than the incident x-rays. The excess energy is taken by recoiling electrons.

This effect cannot be explained by classical theory (by wave nature of light). According to classical model, when X-rays of frequency ν0 is incident on the material containing electrons, then electrons do oscillate & reradiate electromagnetic waves of same frequency ν0. Hence scattered X-rays has same frequency ν0 & same wavelength as that of incident X-rays.

Compton treated this processes as a collision between a photon & an electron. In this treatment, the photon is assumed as a particle of energy

E = hν0 = hc/λ0 ...(1)

Further, the rest mass of photon is zero (because photon travels with the speed of light) hence the momentum of photon can be written as

...(2)

To derive the Compton shift. Δλ, we apply both conservation of energy & momentum.

CONSERVATION OF ENERGY

...(3)

Where hc/λ is energy of scattered X-rays, Ke is kinetic energy of recoiling electron & hc/λ0 is the energy of incoming X-rays. Since the electron may travel with the speed of light, so we must use relativistic expression of Ke in equation (3), and we obtain

...(4)

where m is rest mass of electron and mc2 is the rest mass energy of the electron

where

CONSERVATION OF MOMENTUM

x-component ...(5)

y-component ...(6)

where pe = γmv is the relativistic expression for momentum of recoiling electron.

By eliminating v & φ from equation (4) to (6), we obtain

...(7)

or 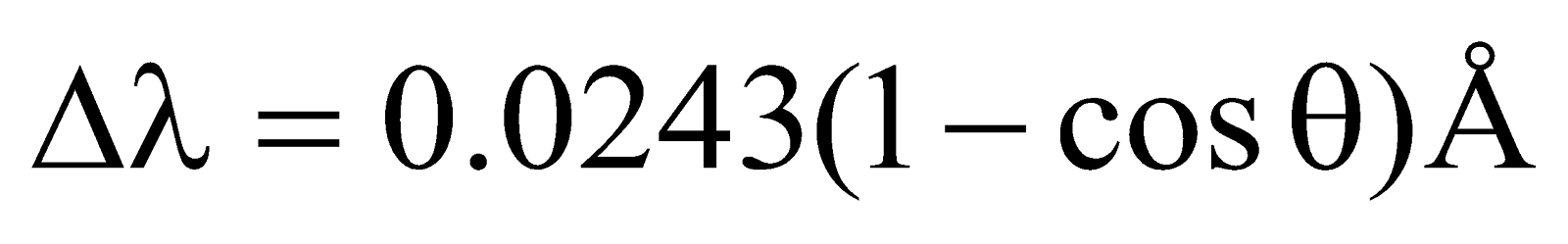...(8)

It is clear from expression (7) that Compton shift Δλ depends on scattering angle θ & not on the wavelength.

KEEP IN MEMORY

1. The wave nature of light shows up in the phenomena of interference, diffraction and polarisation whereas photoelectric effect and Compton effect shows particle nature of light.
2. The maximum kinetic energy of the photoelectrons varies linearly with the frequency of incident radiation but is independent of its intensity.

X-RAYS

• The X-rays were discovered by Prof. Roentgen, a German scientist in 1885. He was awarded Nobel Prize for this discovery in 1901. X-rays are electromagnetic waves.
• The modern apparatus for the production of X-rays was developed by Dr. Coolidge in 1913.
• X-rays are produced when fast moving electrons are suddenly stopped on a metal of high atomic number.

PROPERTIES OF X-RAYS

• They are not deflected by electric or magnetic field.
• They travel with the speed of light.
• There is no charge on X-rays.
• X-rays show both particle and wave nature.
• They are invisible.

CONTINUOUS AND CHARACTERISTIC X-RAYS

Experimental observation and studies of spectra of X-rays reveal that X-rays are of two types and so are their respective spectras. Characteristic X-rays and Continuous X-rays.

CHARACTERISTIC X-RAYS

The spectra of this group consists of several radiations with specific sharp wavelengths and frequency similar to the spectrum (line) of atoms like hydrogen. The wavelengths of this group show characteristic discrete radiations emitted by the atoms of the target material. The characteristic X-rays spectra helps us to identify the element of target material.

When the atoms of the target material are bombard with high energy electrons (or hard X-rays), which possess enough energy to penetrate into the atom, knock out the electron of inner shell (say K shell, n = 1). When an electron is missing in the ‘K’ shell, an electron from next upper shell makes a quantum jump to fill the vacancy in ‘K’ shell. In the transition process the electron radiates energy whose frequency lies in the X-rays region. The frequency of emitted radiation (i.e. of photon) is given by

where R is constant and Ze is effective atomic number. Generally Ze is taken to be equal to Z – σ, where Z is proton number or atomic number of the element and σ is called the screening constant. Due to the presence of the other electrons. The charge of the nucleus as seen by the electron will be different in different shells.

Knocking out e- of K shell by incident electron ei emission of X-ray photon (Kα- series)

Another vacancy is now created in the ‘L’ shell which is again filled up by another electron jump from one of the upper shell (M) which results in the emission of another photon, but of different X-rays frequency. This transition continues till outer shells are reached. Thus resulting in the emission of series of spectral line.

The transitions of electrons from various outer shells to the innermost ‘K’ shell produces a group of X-rays lines called as K-series. These radiations are most energetic and most penetrating. K-series is further divided into …. depending upon the outer shell from which the transition is made.

The jump of electrons from outer shells to ‘L’ shell results in L-Series X-rays and so on.

CONTINUOUS X-RAYS

In addition to characteristic X-rays tubes emit a continuous spectrum also. The characteristic line spectra is superimposed on a continuous X-rays spectra of varying intensities. The wavelength of the continuous X-rays spectra are independent of material. One important feature of continuous X-rays is that they end abruptly at a certain lower wavelength for a given voltage. If an electron beam of energy eV (electron volts) is incident on the target material; the electrons are suddenly stopped. If the whole of the energy is converted to continuous radiation, then λmin (corresponding to energy maximum) = hc/Ve where V is the voltage applied.

The classical theory of electromagnetism states that the suddenly accelerated or decelerated electrons emit radiations of electromagnetic nature called as bremsstrahlung (braking radiation) and wavelength of such radiation is continuous because the loss in energy is statistical. At the peak, the probability of maximum number of electrons producing radiation.

The wavelength of X-rays emitted is minimum corresponding to the electron which hits the target with maximum speed. This electron is completely stopped and will emit the photon of highest energy.

As the electrons lose energy by collision, longer wavelengths are produced the shape of the curve is statistical.

WAVELENGTH OF X-RAYS (DUANE HUNT LAW)

• When an electron is accelerated through a potential difference V then the energy acquired by electron
  
• When these high energy electrons fall on target T of high atomic number, then X-rays are produced, whose wavelength is given by
  
• The energy of X-rays of wavelength λ is
  
• The shortest wavelength of X-rays emitted is
  i.e.

It is called Duane Hunt law.

TYPES OF X-RAYS

• Hard X-rays : The X-rays of high frequency or low wavelength are said to be hard X-rays. They have higher penetrating power.
• Soft X-rays : The X-rays of longer wavelength are called soft X-rays.

MOSELEY’S LAW

Moseley used different elements as target in the X-ray tube. He found that Kα radiation of different elements were different

Mathematically,

where a and b depend on the particular line of the radiation

For Kα, 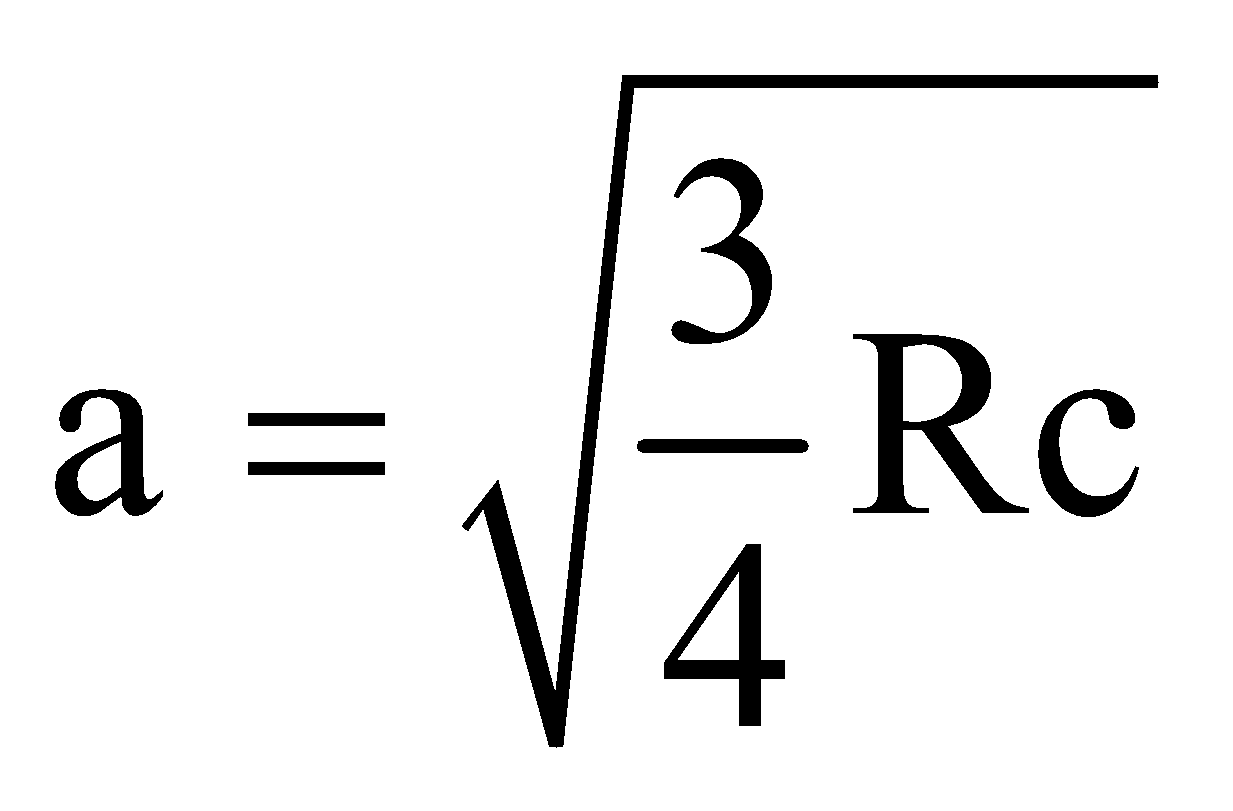and b = 1

where R = Rydberg constant and c = speed of light

In general the wavelength of K - lines are given as

where n = 2, 3, .....

ABSORPTION OF X-RAYS

• X-rays are absorbed by the materials according to the relation I = I0  e–μx, where μ is absorption coefficient and x is the thickness of the material. Here I is the intensity after penetrating the material through distance x and I0 is the initial intensity of the X-rays.
• The coefficient of absorption (μ) of the material is given by
  
  where x1/2 is the distance after traversing which the intensity of X-rays is reduced to half.
• Absorption coefficient depends on the nature of material and wavelength of X-rays i.e. μ = cZ4 λ3.

It means that (a) μz4 (b) μλ3 (c) μν–3.

FLUORESCENCE

Certain substances (like quinine sulphate, fluorescein, barium platinocyanide, uranium oxide etc.), when illuminated with light of high frequency (ultraviolet, violet, etc.) emit light of lower frequency. The phenomenon is called fluorescence.

• When quinine sulphate is illuminated with ultraviolet or violet light it gives out blue light. The fluorescence of barium sulphate as well as uranium oxide gives out green light when illuminated with ultraviolet or violet light.
• The house hold tubes are painted from inside with magnesium tungstate or zinc-beryllium silicate. They are fluorescent materials. The ultraviolet light generated inside the tube falls on the walls, where magnesium tungstate gives blue light and zinc beryllium silicate gives yellow orange light. The mixture of the two produces white light. If the inner side of the tube is painted with cadmium borate it gives fluorescence of pink light and when painted with zinc silicate, it gives fluorescence of green light.
• The fluorescence occurs as long as the material is illuminated.

PHOSPHORESCENCE

Fluorescent materials emit light only so long as light is incident on them. There are certain substances which continue emitting light for some time after the light incident on them is stopped. This phenomenon is called phosphorescence. For example, if we make blue light incident on a zinc-sulphide (ZnS) screen, then it produces phosphorescence of green colour. Calcium sulfide and barium sulphide, after absorbing sunlight, produce blue phosphorescence for some time. Time of phosphorescence is different for different materials.

KEEP IN MEMORY

1. The stopping potential (and hence the maximum kinetic energy of emitted electrons) is independent of the intensity of light but that the saturation current (and hence the number of emitted photoelectrons) is proportional to the intensity.
2. Photoelectric effect doesn't take place below the threshold frequency for the photo metal used.
3. In Compton effect, the change in wavelength is independent of incident photon as well as of the nature of the scatterer, but depends only on the angle of scattering (θ).
4. The quantity is called Compton wavelength.
5. The maximum wavelength change possible in Compton effect is 0.05Å.
6. Compton effect can't be observed for visible light rays.
7. In Compton effect, the direction of recoil electron is given by
   
8. The kinetic energy of recoil electron is given by

9. de-Broglie wavelength of a particle of K.E., Ek is given by
   
10. de-Broglie wavelength for a charged particle with charge q and accelerated through a potential difference V is given by
    
11. de-Broglie wavelength of a material particle at temperature T is given by

, where k is Boltzmann’s constant.

APPLICATION OF X-RAYS

Following are some important and useful applications of X-rays.

• Scientific applications : The diffraction of X-rays at crystals opened new dimension to X-rays crystallography. Various diffraction patterns are used to determine internal structure of crystals. The spacing and dispositions of atoms of a crystal can be precisely determined by using Bragg’s law : nλ = 2d sin θ.
• Industrial applications : Since X-rays can penetrate through various materials, they are used in industry to detect defects in metallic structures in big machines, railway tracks and bridges. X-rays are used to analyse the composition of alloys and pearls.
• In radiotherapy : X-rays can cause damage to the tissues of body (cells are ionized and molecules are broken). So X-rays damages the malignant growths like cancer and tumours which are dangerous to life, when is used in proper and controlled intensities.
• In medicine and surgery : X-rays are absorbed more in heavy elements than the lighter ones. Since bones (containing calcium and phosphorus) absorb more X-rays than the surrounding tissues (containing light elements like H, C, O), their shadow is casted on the photographic plate. So the cracks or fracture in bones can be easily located. Similarly intestine and digestive system abnormalities are also detected by X-rays.

Physics Study Notes

• Physical World
• Units and Measurements
• Motion in a Straight Line
• Motion in a Plane
• Laws of Motion
• Work, Energy and Power
• System of particles and Rotational Motion
• Gravitation
• Mechanical Properties of Solids
• Mechanical Properties of Fluids
• Thermal Properties of Matter
• Thermodynamics
• Kinetic Theory of Gases
• Oscillations
• Waves
• Electric Charges and Fields
• Electrostatic Potential and Capacitance
• Current Electricity
• Moving Charges and Magnetism
• Magnetism and Matter
• Electromagnetic Induction
• Alternating Current
• Electromagnetic Waves
• Ray Optics and Optical Instruments
• Wave Optics
• Dual Nature of Radiation and Matter
• Atoms
• Nuclei
• Semiconductor Electronics : Materials, Devices and Simple Circuits
• Communication Systems
• Experimental Skills in Physics

Study Notes for JEE Main/JEE Advanced

Study Notes for NEET/AIIMS