THERMODYNAMICS
THERMAL EQUILIBRIUM
Two systems are said to be in thermal equilibrium with each other if they have the same temperature.
ZEROTH LAW OF THERMODYNAMICS
If objects A and B are separately in thermal equilibrium with a third object C then objects A and B are in thermal equilibrium with each other.
FIRST LAW OF THERMODYNAMICS
First law of thermodynamics gives a relationship between heat, work and internal energy.
HEAT
It is the energy which is transferred from a system to surrounding or vice-versa due to temperature difference between system and surroundings.
- It is a macroscopic quantity.
- It is path dependent i.e., it is not point function.
- If system liberates heat, then by sign convention it is taken negative, If system absorbs heat, it is positive.
WORK
It is the energy that is transmitted from one system to another by a force moving its points of application. The expression of work done on a gas or by a gas is
where V1 is volume of gas in initial state and V2 in final state.
- It is also macroscopic and path dependent function.
- By sign convention it is +ive if system does work (i.e., expands against surrounding) and it is -ive, if work is done on system (i.e., contracts).
- In cyclic process the work done is equal to area under the cycle and is -ive if cycle is anti-clockwise and +ive if cycle is clockwise (shown in fig.(a) and (b)).
INTERNAL ENERGY
The internal energy of a gas is sum of internal energy due to molecular motion (called internal kinetic energy UK) and internal energy due to molecular configuration (called internal potential energy UP.E.)
i.e., U = UK + UP.E. ……(1)
- In ideal gas, as there is no intermolecular attraction, hence
(for n mole of ideal gas)
- Internal energy is path independent i.e., point function.
- In cyclic process, there is no change in internal energy (shown in fig.)
i.e., dU =Uf – Ui = 0
⇒ Uf = Ui
- Internal energy of an ideal gas depends only on temperature eq.(2).
First law of thermodynamics is a generalisation of the law of conservation of energy that includes possible change in internal energy.
FIRST LAW OF THERMODYNAMICS
If certain quantity of heat dQ is added to a system, a part of it is used in increasing the internal energy by dU and a part is use in performing external work done dW
i.e., 
The quantity dU (i.e., dQ – dW) is path independent but dQ and dW individually are not path independent.
APPLICATIONS OF FIRST LAW OF THERMODYNAMICS
- In isobaric process P is constant
so 
so dQ = dU + dW = n CP dT
- In cyclic process heat given to the system is equal to work done (area of cycle).
- In isothermal process temperature T is constant and work done is
Since, T = constant so for ideal gas dU = 0
Hence,  (for ideal gas)
(for ideal gas)
- In isochoric process W = 0 as V = constant
It means that heat given to system is used in increasing internal energy of the gas.
- In adiabatic process heat given or taken by system from surrounding is zero
i.e., dQ = 0
It means that if system expands dW is +ive and dU is –ive (i.e., temperature decrease) and if system contracts dW is –ive and dU is +ive (i.e., temperature increase).
THERMODYNAMIC PROCESSES
ISOTHERMAL PROCESS
If a thermodynamic system is perfectly conducting to surroundings and undergoes a physical change in such a way that temperature remains constant throughout, then process is said to be isothermal process.
For isothermal process, the equation of state is
PV = nRT = constant, where n is no. of moles.
For ideal gas, since internal energy depends only on temperature.
or 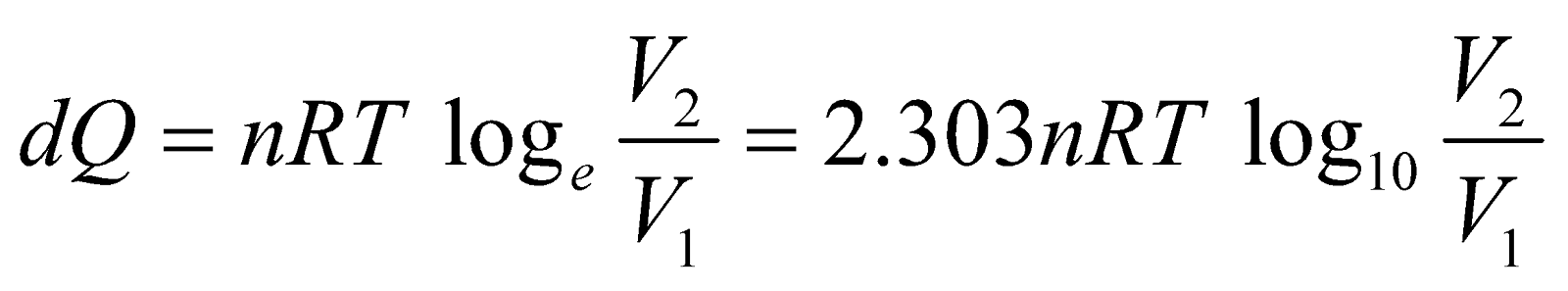
ADIABATIC PROCESS
If system is completely isolated from the surroundings so that no heat flows in or out of it, then any change that the system undergoes is called an adiabatic process.
For ideal gas, dQ = 0
dU = μCVdT (for any process)
(where PVγ = K = constant)
where PVγ = constant is applicable only in adiabatic process. Adiabatic process is called isentropic process (in these process entropy is constant).
ISOBARIC PROCESS
A process taking place at constant pressure is called an isobaric process. In this process
dQ = n CpdT, dU = n CVdT and dW = P(V2–V1)
ISOCHORIC PROCESS
A process taking place at constant volume is called isochoric process.
In this process, dQ = dU =n CVdT and dW = 0
CYCLIC PROCESS
In this process the initial state and final state after traversing a cycle (shown in fig.) are same.
In cyclic process, dU = 0 = Uf – Ui and dW = area of cycle = area (abcd)
Slope of adiabatic and isothermal curve
For isothermal process PV = constant
On differentiating, we get PdV + VdP = 0
And slope of isothermal curves
For adiabatic process PVγ = constant
On differentiation, we get slope of adiabatic curve
It is clear from equation (1) and (2) that the slope of adiabatic curve is more steeper than isothermal curve as shown by fig by γ time (γ = CP/CV)
GRAPHS OF THERMODYNAMIC PROCESSES
- In the figure (i) P–V graph the process ab is isothermal, bc is isobaric and ca is isochoric.
The fig (ii) is the P–T diagram of fig (i)
- Figure below shows P–V diagrams for two processes.
The heat absorbed in process I is more than that in II. Because, area under process I is also more than area under process II. The work done in the process I is more than that in II. Also, the change in internal energy is same in both cases.
- The P–V and corresponding V–T diagram for a cyclic process abca on a sample of constant mass of ideal gas are shown below:
- For isochoric process, the P–V, V–T and P–T graphs :
- For isobaric process, the P – V, P – T and V – T graphs :
- For isothermal process, the P – V, V – T and P – T graphs :
KEEP IN MEMORY
- In thermodynamics heat and work are not state variables, whereas internal energy is a state variable.
- For ideal-gas
- relation between P and V is PVγ = constant
- relation between V and T is TV γ–1 = constant
- relation between P and T is TγP1–γ = constant
- A quasi-static process is an infinitely slow process such that system remains in thermal and mechanical equilibrium with the surroundings throughout.
- Pressure, volume, temperature and mass are state variables. Heat and work are not state variables.
- A graphical representation of the state of a system with the help of two thermodynamic variables is called indicator diagram.
REVERSIBLE AND IRREVERSIBLE PROCESS
REVERSIBLE PROCESS
A process which can proceed in opposite direction in such a way that the system passes through the same states as in direct process and finally the system and the surroundings acquire the initial conditions.
CONDITIONS FOR A PROCESS TO BE REVERSIBLE
- The process must be extremely slow.
- There should no loss of energy due to conduction, or radiation. The dissipating forces should not be in the system.
- The system must always be in thermal and chemical equilibrium with the surroundings.
Examples : Fusion of ice, vaporisation of water, etc.
IRREVERSIBLE PROCESS
The process which cannot be traced back in the opposite direction is defined as irreversible process.
Examples : Work done against friction, magnetic hysteresis.
In nature all process are irreversible, because no natural process can fulfil the requirement of a reversible process.
HEAT ENGINE
A heat engine is a device which converts heat energy into mechanical energy.
Efficiency of heat engine is given by
where Q2 = amount of heat rejected per cycle to the sink (of temp T2)
Q1 = amount of heat energy absorbed per cycle from the source (of temp T1).
The efficiency of heat engine η is never greater than unity, η =1 only for ideal engine & for practical heat engine η < 1.
REFRIGERATOR AND HEAT PUMP
Refrigerator or heat pump is a heat engine running in backward direction i.e. working substance (a gas) takes heat from a cold body and gives out to a hotter body with the use of external energy i.e. electrical energy. A heat pump is the same as a refrigerator.
The coefficient of performance of refrigerator or heat pump is
where T2 is temperature of cold body and T1 is temperature of hot body.
CARNOT ENGINE
Carnot devised an ideal engine which is based on a reversible cycle of four operations in succession : isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression.
Efficiency of Carnot engine,
The points B and C are connected by an adiabatic path as are the points D and A. Hence, using this eqn. and the adiabatic gas eqn.
T1V2(γ – 1) = T2 V3(γ – 1) and T1V1(γ – 1) = T2 V4(γ – 1).
Combination of the above eqns. gives  , and,
, and,
or, 
The percentage efficiency of Carnot’s engine,
The efficiency of a Carnot engine is never 100% because it is 100% only if temperature of sink T2 = 0 which is impossible.
In a Carnot cycle, 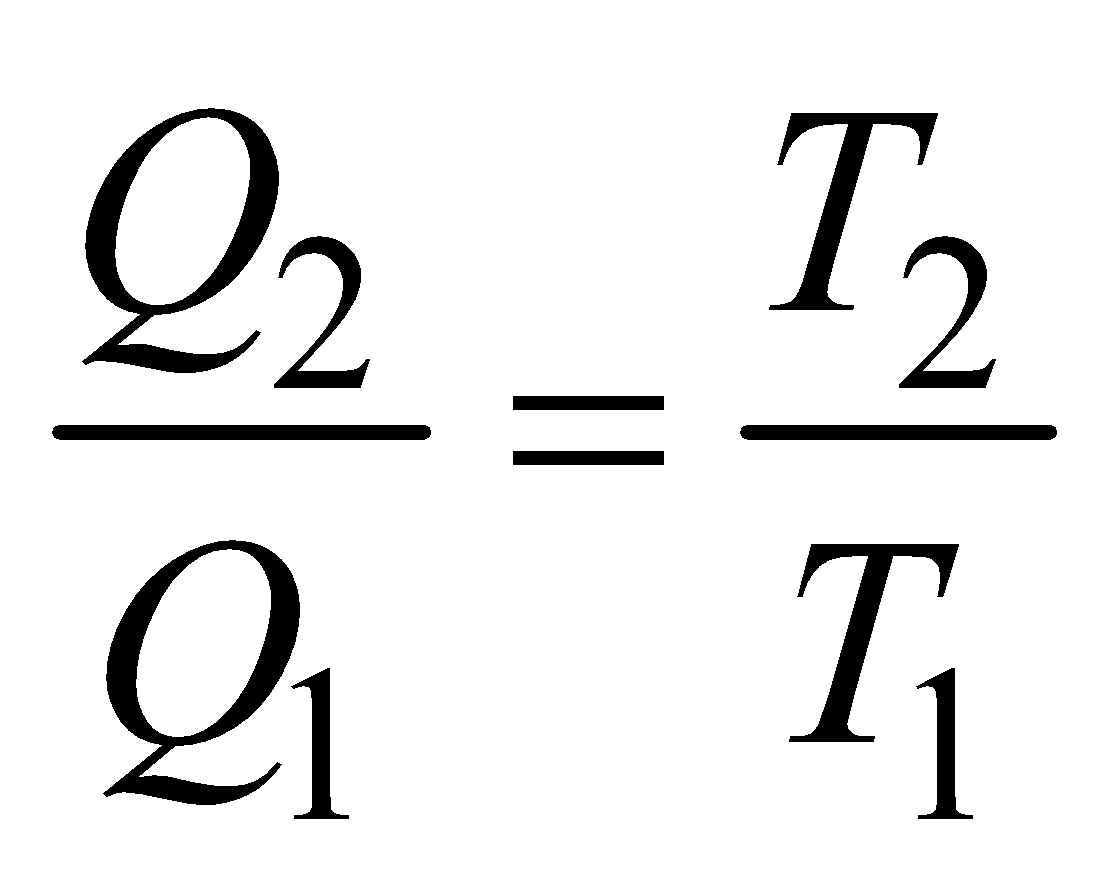 or
or
CARNOT THEOREM
No irreversible engine (I) can have efficiency greater than Carnot reversible engine (R) working between same hot and cold reservoirs.
i.e.,  or
or 
SECOND LAW OF THERMODYNAMICS
It states that it is impossible for a self acting machine unaided by any external agency, to transfer heat from a body at a lower temperature to a body at higher temperature.
It is deduced from this law that the efficiency of any heat engine can never be 100%.
ENTROPY
Entropy is a measure of disorder of the molecular motion of a system. The greater the disorder, the greater is the entropy. The change in entropy is given by
Clausius inequality
or, dQ = TdS ≥ dU + PdV
Also, S = K logeω
- Energy entering a body increases disorder
- Energy leaving a body decreases disorder
When a hot body is brought into thermal contact with a cold body for a short time, then :
- Each body will experience a change in the entropy of its particle.
- The hot body experiences a decrease in entropy (a negative change) of magnitude
- The cold body experiences an increase in entropy (a positive change) of magnitude
- The net change in entropy
The effect of naturally occurring processes is always to increase the total entropy (or disorder) of the universe.










