Mechanical Properties of Fluids | Physics Notes for IITJEE/NEET

MECHANICAL PROPERTIES OF FLUIDS

FLUIDS

Fluid is something that can flow. All liquids and gases are fluids. The force exerted normally at a unit area of the surface of a fluid is called fluid pressure.

i.e.,  P =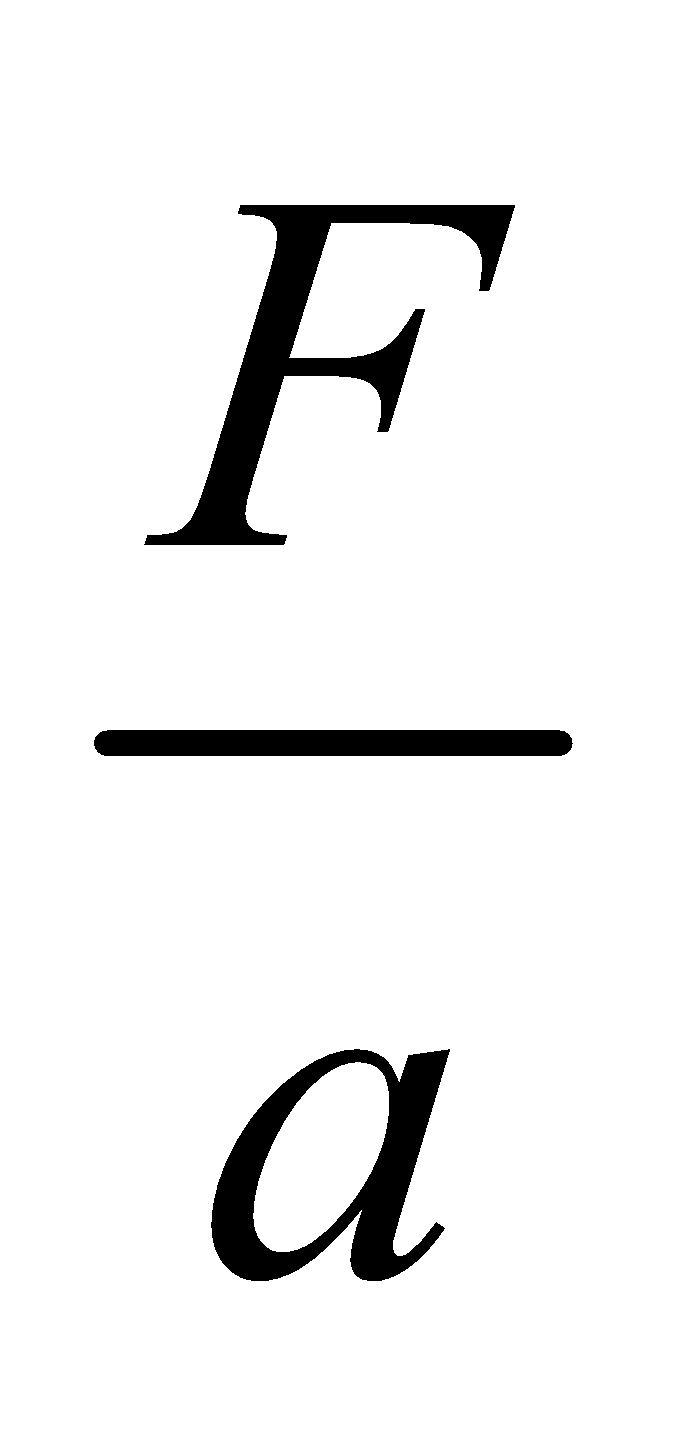

Its S.I. unit is Nm–2 or Pascal. Its dimensions are [ML–1T–2].

PASCAL'S LAW AND ITS APPLICATIONS

PASCAL'S LAW
Pressure in a fluid in equilibrium is the same everywhere, if the effect of gravity is neglected.

ANOTHER FORM OF PASCAL'S LAW

The excess pressure, applied anywhere in a mass of confined incompressible fluid is transmitted by the fluid in all directions without being diminished in magnitude.

APPLICATIONS OF PASCAL'S LAW  

Hydraulic lift : Its working is based on Pascal's law. A piston of small cross-sectional area (a) exerts a force (f) on the liquid.

The pressure is transmitted undiminished to the larger cylinder of cross-sectional area A.

Hydraulic brakes also work on pascal's law.   

ATMOSPHERIC, HYDROSTATIC AND GAUGE PRESSURE

ATMOSPHERIC PRESSURE

The atmosphere exerts pressure on the  earth's surface. The atmospheric pressure at sea level is given by P0  = 1.01 × 105 Pa

HYDROSTATIC PRESSURE

The hydrostatic pressure at a depth h below the surface of a fluid is given by

P = hρg, where ρ is the density of the fluid, g acceleration due to gravity and h is the depth of the liquid column.

GAUGE PRESSURE

The pressure at any point in a fluid is equal to the sum of the atmospheric pressure acting on its surface and the hydrostatic pressure due to the weight of the fluid above that point which is at a depth h below the surface of the fluid.

The gauge pressure is given by

P = P0 + hρg

or,        P – P0 = hρg

BUOYANCY AND ARCHIMEDES' PRINCIPLE

BUOYANCY

If a body is partially or wholly immersed in a fluid, it experiences an upward force due to the fluid surrounding it.  The phenomenon of force exerted by fluid on the body called buoyancy and the force is called buoyant force or upthrust.

A body experiences buoyant force whether it floats or sinks, under its own weight or due to other forces applied on it.

ARCHIMEDES' PRINCIPLE  

When any body is immersed (totally or partially) in a liquid it appears to lose part of its weight and the apparent loss of weight is equal to the weight of liquid displaced.

Let a body of weight W is immersed in a fluid and W' is upthrust on it then

• if W > W', then body will sink.
• if W = W', then the body floats with whole or some part of its volume inside the fluid.

Let V be the volume of a body of density d and V' be the volume of liquid of density ρ displaced. If the body floats then Vd = V′ρ

∴gives the fraction of the volume inside the liquid in which the body floats.

Also, body immersed in a fluid experiences an upward buoyant force equivalent to the weight of the fluid displaced by it.  

The proof of this principle is very simple. Imagine a body of arbitrary shape completely immersed in a liquid of density ρ as shown in the figure (a). A body is being acted upon by the forces from all directions. Let us consider a vertical element of height h and cross-sectional area dA (as shown in the figure (b)).

(a)     (b)

The force acting on the upper surface of the element is F1 (downward) and that on the lower surface is F2 (upward). Since F2 > F1, therefore, the net upward force acting on the element is   dF = F2 – F1

It can be easily seen from the figure (b), that

and so

Also, h2 – h1 = h and d(dA) = dV

∴ The net upward force is

Hence, for the entire body, the buoyant force is the weight of the volume of the fluid displaced.

The buoyant force acts through the centre of gravity of the displaced fluid.

KEEP IN MEMORY

1. The pressure is perpendicular to the surface of the fluid.
2. The upthrust on a body immersed in a liquid does not depend on the mass, density or shape of the body. It only depends on the volume of the body.
3. The weight of the plastic bag full of air is same as that of the empty bag because the upthrust is equal to the weight of the air enclosed.
4. The cross-section of the water stream from a top decreases as it goes down in accordance with the equation of continuity.
5. We cannot sip a drink with a straw on the moon, because there is no atmosphere on the moon.
6. The line joining the centre of gravity and centre of buoyancy is called central line.
7. Metacenter - is a point where the vertical line passing through the centre of buoyancy intersects the central line.
8. The floating body is in stable equilibrium when the metacenter is above the centre of gravity (centre of gravity is below the centre of buoyancy).
9. The floating body is in the unstable equilibrium when the metacenter lies below the centre of gravity (centre of gravity is above the centre of buoyancy).
10. The floating body is in the neutral equilibrium when centre of gravity coincides with the metacenter (centre of gravity coincides with the centre of buoyancy).
11. The wooden rod cannot float vertically in a pond of water because centre of gravity lies above the metacenter.
12. (i) If a body just floats in a liquid (density of the body is equal to the density of liquid) then the body sinks if it is pushed downwards.

(ii) If two bodies have equal upthrust when just immersed in a liquid, both will have the same volume.

(iii) If a person floats on his back on the surface of water, the apparent weight of person is zero.

13. The hydrometer can be used to measure density of the liquid or fluid.

RELATIVE DENSITY (OR SPECIFIC GRAVITY)

Liquids may be treated as incompressible. Hence their density may be assumed to be constant throughout.

Relative density =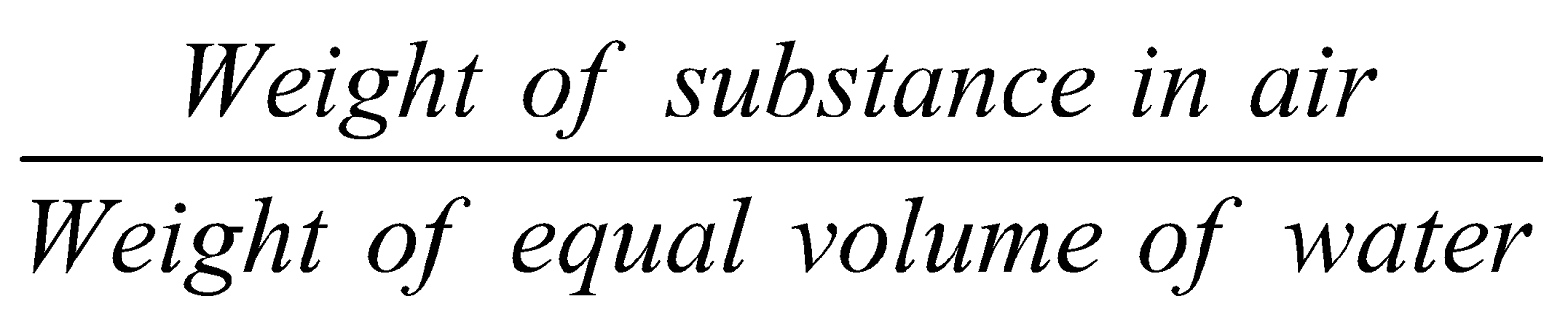

Density in SI system = 1000 × density in the cgs system.

• The density of liquid of bulk modulus B at a depth h is given by whereis the density of liquid on its surface and is the average density of liquid.
• The density of liquid changes with pressure as

where change in pressure and B = bulk modulus of liquid.

• If two liquids of masses m1, m2 and densities ρ1, ρ2 are mixed together, then the density of the mixture is given by

And if m1 = m2 but different densities are mixed together, then the density of the mixture is harmonic mean of the densities.   

i.e.,  or

• If two drops of same volume but different densities are mixed together, then the density of the mixture is the arithmetic mean of the densities.

i.e.,   (as )

SURFACE TENSION    

It is defined as the force per unit length acting at right angles on either side of an imaginary line drawn on the free surface of the liquid.

i.e.,  

The surface tension is also defined as the work required to increase unit area of that liquid film.

Its SI unit is N/m or J/m2 and dimensions are [ML0T–2].

KEEP IN MEMORY

1. The liquid surface always acquires minimum surface area due to surface tension (ST). So, the small droplet of any liquid is always spherical.
2. The ST is a molecular phenomenon as ST is due to 'cohesion' between the molecules of a liquid.
3. The force of attraction between the molecules of the same substance is called a cohesive force and that between molecules of different substance is called adhesive force.
4. The molecular range is the maximum distance (10–9 m) upto which the molecules attract each other.
5. In general the ST of liquids decreases with increase in temperature but the ST of molten Cadmium and Copper increases with increase in temperature.
6. If the impurity is completely soluble then on mixing it in the liquid, its surface tension increases. For example on dissolving ionic salts in small quantities in a liquid, its surface tension increases. On dissolving salt in water, its surface tension increases.
7. If the impurity is partially soluble in a liquid, then its surface tension decreases. For example on mixing detergent or phenol in water its surface tension decreases.
8. On increasing temperature surface tension decreases. At critical temperature and boiling point it becomes zero. Surface tension of water is maximum at 4°C.

ANGLE OF CONTACT

The angle between the tangent to the liquid surface and the tangent to the solid surface at the point of contact (inside the liquid) is known as angle of contact.

Some values of angle of contact of solid and liquid :

KEEP IN MEMORY

1. The value of angle of contact lies between 0º and 180º. For pure water and glass it is 0º, for tap water and glass it is 8º and for mercury and glass it is 135º.
2. For all those liquids which wet the solid surface and which rise up in a capillary tube, the angle of contact is an acute angle (θ < 90°), e.g. water and glass.
3. For all those liquids which do not wet a solid surface and which depress in a capillary tube, the angle of contact is an obtuse angle (θ > 90°), e.g. glass and mercury.
4. For all those liquids which neither rise nor get depressed in a capillary tube, the angle of contact is right angle (θ = 90°), e.g. silver and water.
5. Angle of contact depends on impurities, water proofing agent, surface in contact and temperature. Angle of contact θC ∝ T where T is the temperature.

CAPILLARITY

The phenomenon of rise or fall of liquids in capillary tube is known as capillarity.

The rise or fall of a liquid in a capillary tube is given by

where T = surface tension,
θ = angle of contact,
ρ = density of liquid,  
r = radius of capillary tube,
R = radius of meniscus.

• If capillary tube is of insufficient length l (i.e. l < h), then the liquid rises to a full height h with radius R' such that hR = lR'
• When the capillary tube is tilted from vertical by an angle α, then the vertical height h of liquid column remains the same. The length of liquid in capillary increases such that or .

According to Zurin's law capillary rise where r is the radius of the capillary tube.

KEEP IN MEMORY

1. Work done in forming a liquid drop of radius R, surface tension T is, W = 4πR2T.
2. Work done in forming a soap bubble of radius R, surface tension T is, W = 2×4πR2T = 8πR2T.
3. When n no. of smaller drops of liquid, each of radius r, surface tension T are combined to form a bigger drop of radius R then .
4. The surface area of bigger drop = 4πR2 = 4πn2/3 r2. It is less than the area of n smaller drops.

SHAPE OF LIQUID MENISCUS

The pressure on the concave side is always greater than the pressure on the convex side.

PA=P0–2Τ/r  PA=P0+2T/r

(r is radius of meniscus)

Excess pressure of liquid drop and soap bubble :

• Excess of pressure for spherical soap bubble is p = 4T/r and excess of pressure for liquid drop and air bubble in a liquid is p = 2T/r.
• Excess of pressure within a cylindrical liquid drop p = T/R
• Excess of pressure within a cylindrical soap bubble  p = 2T/R

where T = surface tension, R = radius of the cylindrical drop.

KEEP IN MEMORY

1. Work done in breaking a liquid drop of radius R into n equal small drops = ; where T = surface tension.
2. Work done in breaking a soap bubble of radius R into n equal small drops = ; where T = surface tension.

FLOW OF LIQUIDS

The motion of fluids are of following four types :

STREAMLINE MOTION

When fluid in motion, if fluid particles preceding or succeeding a fluid particle follow the same path, then the path is called streamline and the motion of the fluid is called streamline motion. This type of motion takes place in non-viscous fluids having very small speed.

Principle of continuity : When incompressible, non-viscous liquid flows in non-uniform tube then in streamline flow product of area and velocity at any section remains same.

The mass of liquid flowing in equals the mass flowing out.

i.e., m1 = m2

or, v1A1ρ1 Δt = v2 A2ρ2Δt ..... (1)

As we have considered the fluid incompressible thus,   

v1A1 = v2A2  or     Av = constant ....(2)

(Since  ρ1 = ρ2)

Equations (1) and (2) are said to be as equation of continuity.

STEADY STATE MOTION

In a liquid in motion, when liquid particles, crossing a point, cross it with same velocity, then the motion of the liquid is called steady state motion. This type of motion takes place in non-viscous liquids having very small speed.

LAMINAR MOTION

Viscous liquids flow in bounded region or in a pipe, in layers and when viscous liquid is in motion, different layers have different velocities. The layers in contact with the fixed surface has least velocity and the velocity of other parallel layers increases uniformly and continuously with the distance from the fixed surface to the free surface of the liquid. This is called laminar motion of the liquid.

TURBULENT MOTION

When the velocity of a liquid is irregular, haphazard and large, i.e. Beyond a limiting value called critical velocity the flow of liquid loses steadiness then  the motion of the liquid is called turbulent motion.

Critical velocity Vc

Here η is called coefficient of viscosity.

VISCOSITY

The internal friction of the fluid, which tends to oppose relative motion between different layers of the fluid is called viscosity.

The viscous force between two layers of a fluid of area A having a velocity gradient is given by

where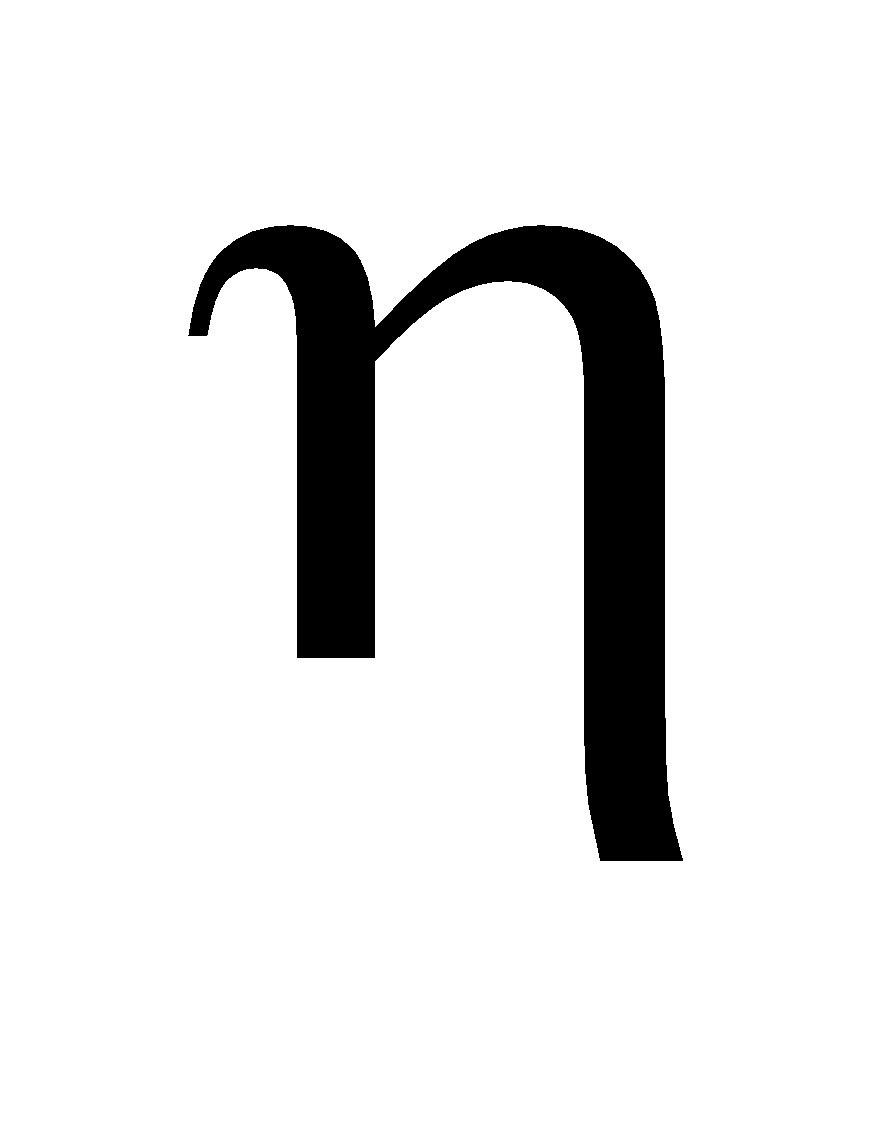 is called the coefficient of viscosity.

Its S.I. unit is poiseuille or decapoise.

The C.G.S. unit is called poise.

1 decapoise = 10 poise.

EFFECTS ON VISCOSITY

• Effect of temperature : On increasing temperature viscosity of a liquid decreases.
• Effect of pressure : On increasing pressure viscosity of a liquid increases but viscosity of water decreases.

KEEP IN MEMORY

1. The viscosity of gases increases with increase of temperature, the rate of diffusion increases.
2. The viscosity of liquids decrease with increase of temperature, because the cohesive force between the liquid molecules decreases with increase of temperature.

CRITICAL VELOCITY

It is the maximum velocity of a fluid above which a stream line flow changes to a turbulent flow, i.e. it is the maximum velocity of a liquid below which its flow remains streamline.

• Reynold's formula for critical velocity is

 or  

where N = Reynold's no., = coefficient of viscosity,

ρ = density of liquid;

r = radius of tube,

N = 1000 for narrow tube.

• (a) If 0 < N < 2000 then the flow is laminar

(b) If 2000 < N < 3000 then flow of liquid is unstable and may change from laminar to turbulent

(c) If N > 3000, then the flow is turbulent.

• When velocity of fluid is less than its critical velocity then the flow of liquid is determined by its viscosity, its density has no effect on its flow.
• When the velocity of liquid is more than its critical velocity then its flow is determined by its density, where viscosity has little effect on its flow. For example lava from volcano is highly thick, despite that it comes out with high speed.
• When the flow of liquid is streamline and when V > Vc then the flow of liquid is turbulent.

for same liquid, which is flowing in two tubes of radii r1 and r2 respectively.      

• The critical velocity of a liquid with high viscosity and smaller radius is higher than that of a liquid with low viscosity and greater radius.

REYNOLD'S NUMBER (N)

It is pure number which determines the nature of flow of liquid through a pipe.

 
N is a dimensionless quantity and carries no unit.

BERNOULLI'S THEOREM

For non-viscous, incompressible, streamline flow of fluids the sum of pressure per unit volume, potential energy per unit volume and Kinetic energy per unit volume remain constant.

i.e.,  + gh +v2 = constant

where ρ = density of fluid.

When h = 0 then

Bernoulli's theorem is strictly applicable for an ideal fluid.
An ideal fluid is one which is (a) incompressible (b) streamline (c) irrotational and (d) non-viscous.

APPLICATIONS OF BERNOULLI’S PRINCIPLE

• Wings of aeroplane : The wings of the aeroplane are having tapering. Due to this specific shape of wings when the aeroplane runs, air passes at higher speed over it as compared to its lower surface. This difference of air speeds above and below the wings, in accordance with Bernoulli's principle, creates a pressure difference, due to which an upward force called 'dynamic lift' (= pressure difference  area of wing) acts on the plane. If this force becomes greater than the weight of the plane, the plane will rise up.

• Ball moving without spin : The velocity of fluid (air) above and below the ball at corresponding points is the same resulting in zero pressure difference. The air therefore, exerts no upward or downward force on the ball.
• Ball moving with spin : A ball which is spinning drags air along with it. If the surface is rough more air will be dragged. The streamlines of air for a ball which is moving and spinning at the same time. The ball is moving forward and relative to it the air is moving backwards. Therefore, the velocity of air above the ball relative to it is larger and below it is smaller. The streamlines thus get crowded above and rarified below.

This difference in the velocities of air results in the pressure difference between the lower and upper faces and their is a net upward force on the ball. This dynamic lift due to spinning is called Magnus effect.

Some other applications of Bernoulli’s principle :

• The action of carburetor, sprayer or atomizer based on Bernoulli’s principle.
• The action of bunsen burner, exhaust pump etc.
• Air foil or lift on aircraft wing works on Bernoulli’s principle.
• Motion of a spinning ball  i.e., magnus effect.
• Blowing of roofs by wind storms etc. based on Bernoulli's principle.

STOKE’S LAW  

When a solid moves through a viscous medium, its motion is opposed by a viscous force depending on the velocity and shape and size of the body. The energy of the body continuously decreases in overcoming the viscous resistance of the medium. This is why cars, aeroplanes etc. are shaped streamline to minimize the viscous resistance on them.

The viscous drag on a spherical body of radius r, moving with velocity v, in a viscous medium of viscosity η is given by  

This relation is called Stokes' law. .

Importance of Stoke’s law

• It is used in the determination of electronic charge with the help of millikan's experiment.
• It accounts the formation of clouds.
• It accounts why the speed of raindrops is less than that of a body falling freely with a constant velocity from the height of clouds.
• It helps a man coming down with the help of a parachute.

TERMINAL VELOCITY

When a spherical body is allowed to fall through viscous medium, its velocity increases till the viscous drag plus upthrust is equal to the weight of the body. After that body moves with constant velocity, called terminal velocity.

The terminal velocity is given by

where d = density of body,

= density of medium,

η = coefficient of viscosity of medium,

R = radius of the spherical body.

From terminal velocity, ,  i.e. greater the viscosity, smaller is the terminal speed.

FLOW OF LIQUID THROUGH TUBE/PIPE

Poiseuille's equation is , where p is the pressure difference between the two ends of the tubes, r is the radius, l is the length of the tube and η is the coefficient of viscosity, Q = rate of flow of liquid.

Equivalent liquid resistance = , when tube are joined in series.

It means that liquid flow through capillary tube is similar to flow of electric current through a conductor i.e., Q (rate of liquid flow) corresponds to I (rate of flow of charge), pressure difference similar to potential difference.

When two tubes are joined in series then the volume of fluid flowing through the two tubes is the same but the pressure difference across the two tubes is different. The total pressure difference, P = P1 + P2.

If two tubes are joined in parallel then the pressure difference across the two tubes is the same but the volume of fluid flowing through the two tubes is different. The total volume of the fluid flowing through the tube in one second is Q = Q1 + Q2.

VELOCITY  OF EFFLUX AND TORRICELLI'S THEOREM

• Torricelli's theorem : For liquid filled in a tank upto a height H having a hole O at a depth h from free level of liquid through which the liquid is coming out,  velocity of efflux of liquid v =.
• Time taken by the liquid in falling from hole to ground level
  

• The horizontal range covered by the liquid

x = horizontal velocity (v) ×time (t)

For maximum horizontal range, differentiating both side w.r.t. h and we get h = H/2, the range is maximum.

KEEP IN MEMORY

1. The cross-section of the water stream from a top decreases as it goes down in accordance with the equation of continuity.
2. When a hale blows over a roof, the force on the roof is upwards.
3. Sudden fall in atmospheric pressure predicts possibility of a storm.
4. Venturimeter is a device used for the measurement of the rate of flow of incompressible fluid through a tube. Its working is based on Bernoulli’s principle.

Physics Study Notes

• Physical World
• Units and Measurements
• Motion in a Straight Line
• Motion in a Plane
• Laws of Motion
• Work, Energy and Power
• System of particles and Rotational Motion
• Gravitation
• Mechanical Properties of Solids
• Mechanical Properties of Fluids
• Thermal Properties of Matter
• Thermodynamics
• Kinetic Theory of Gases
• Oscillations
• Waves
• Electric Charges and Fields
• Electrostatic Potential and Capacitance
• Current Electricity
• Moving Charges and Magnetism
• Magnetism and Matter
• Electromagnetic Induction
• Alternating Current
• Electromagnetic Waves
• Ray Optics and Optical Instruments
• Wave Optics
• Dual Nature of Radiation and Matter
• Atoms
• Nuclei
• Semiconductor Electronics : Materials, Devices and Simple Circuits
• Communication Systems
• Experimental Skills in Physics

Study Notes for JEE Main/JEE Advanced

Study Notes for NEET/AIIMS