Units and Measurements | Physics Notes for IITJEE/NEET

UNITS AND MEASUREMENTS

PHYSICAL QUANTITY

All the quantities in terms of which laws of physics are described and which can be measured directly or indirectly are called physical quantities. For example mass, length, time, speed, force etc.

TYPES OF PHYSICAL QUANTITY

1. Fundamental quantities : The physical quantities which do not depend upon other physical quantities are called fundamental or base physical quantities. e.g. mass, length, time temperature electric current, luminous intensity and amount of substance.
2. Derived quantities : The physical quantities which depend on fundamental quantities are called derived quantities
   e.g. speed, acceleration, force, etc.

UNIT

The process of measurement is a comparison process.

Unit is the standard quantity used for comparison.

The chosen standard for measurement of a physical quantity, which has the same nature as that of the quantity is called the unit of that quantity.

Choice of a unit (Characteristics of a unit):

• It should be suitable in size (suitable to use)
• It should be accurately defined (so that everybody understands the unit in same way)
• It should be easily reproducible.
• It should not change with time.
• It should not change with change in physical conditions i.e., temperature, pressure, moisture etc.
• It should be universally acceptable.

Every measured quantity (its magnitude) comprises of a number and a unit. Ex: In the measurement of time, say

If Q is the magnitude of the quantity (which does not depend on the selection of unit) then

Q = n u = n1 u1 = n2 u2 ⇒

Where u1 and u2 are the units and n1 and n2 are the numerical values in two different system of units.

FUNDAMENTAL (OR BASE) AND DERIVED UNITS

Fundamental units are those, which are independent of unit of other physical quantity and cannot be further resolved into any other units or the units of fundamental physical quantities are called fundamental or base units. e.g., kilogram, metre, second etc,

All units other than fundamental are derived units (which are dependent on fundamental units) e.g., unit of speed (ms–1) which depends on unit of length (metre) and unit of time (second), unit of momentum (Kgms–1) depends on unit of mass, length and time etc.

SYSTEM OF UNITS

A system of units is a complete set of fundamental and derived units for all physical quantities.

DIFFERENT TYPES OF SYSTEM OF UNITS

F.P.S. (Foot - Pound - Second) system. (British engineering system of units.): In this system the unit of length is foot, mass is pound and time is second.

C.G.S. (Centimetre - Gram - Second) system. (Gaussian system of units): In this system the unit of length is centimetre, mass is gram and time is second.

M.K.S (Metre - Kilogram - Second) system. This system is related to mechanics only. In this system the unit of length is metre, mass is kilogram and time is second.

S.I.  (International system) units. (Introduced in 1971) Different countries use different set of units. To avoid complexity, by international agreement, seven physical quantities have been chosen as fundamental or base physical quantities and two as supplementary. These quantities are

MERITS OF S.I. UNITS

• SI is a coherent system of units: This means that all derived units are obtained by multiplication and division without introducing any numerical factor.
• SI is a rational system of units: This is because it assigns only one unit to a particular physical quantity.
• SI is an absolute system of units: There is no gravitational unit in this system.
• SI system is applicable to all branches of science.

CONVENTIONS OF WRITING OF UNITS AND THEIR SYMBOLS

• Unit is never written with capital initial letter.
• For a unit named after scientist the symbol is a capital letter otherwise not.
• The unit or symbol is never written in plural form.
• Punctuations marks are not written after the symbol.

DEFINITIONS OF FUNDAMENTAL UNITS

• Metre : One metre is equal to 1650763.73 wavelength in vacuum of the radiation corresponding to transition between the levels 2p10 and 5d5 of the krypton – 86 atom

or
The distance travelled by light in vacuum in second is called 1 metre.

• Kilogram : The mass of cylinder (of height and diameter 39 cm) made of Platinum-iridium alloy kept at International Bureau of weights and measures in paris is defined as 1kg.
• Second : It is the duration of 9,192,631,770 periods of radiation corresponding to the transition between the two hyperfine levels of the ground state of Caesium (133) atom.
• Ampere : It is the current which when flows through two infinitely long straight conductors of negligible cross-section placed at a distance of one metre in air or vacuum produces a force of 2 × 10–7 N/m between them.
• Candela : It is the luminous intensity in a perpendicular direction, of a surface of 1/600,000 square metre of a black body at the temperature of freezing platinum under a pressure of 1.013 × 105 N/m2.
• Kelvin : It is the 1/273.16 part of thermodynamic temperature of triple point of water.
• Mole : It is the amount of substance which contains as many elementary entities as there are in 0.012 kg of Carbon-12.

S.I. PREFIXES

The magnitudes of physical quantities vary over a wide range. For example, the atomic radius, is equal to 10–10m, radius of earth is 6.4×106 m and the mass of electron is 9.1×10–31 kg. The internationally recommended standard prefixes for certain powers of 10 are given in the table:

SOME IMPORTANT PRACTICAL UNITS

• For large distance (macro-cosm)

Astronomical unit: It is the average distance of the centre of the sun from the centre of the earth.
1 A.U. = 1.496 × 1011m

Light year: It is the distance travelled by the light in vacuum in one year.
1 ly = 9.46 × 1015m

Parsec: One parsec is the distance at which an arc 1A.U. long subtends an angle of one second.
1 parsec = 3.1 × 1016m

• For small distance (micro-cosm)

1 micron = 10–6m
1 nanometre = 10–9m
1 angstorm = 10–10m
1 fermi = 10–15m

• For small area
  1 barn = 10–28m2
  
• For heavy mass
  1 ton = 1000kg
  1 quintal = 100kg
  1 slug = 14.57kg
  1 C.S.L (chandrasekhar limit) = 1.4 times the mass of the sun
  
• For small mass
  1 amu = 1.67 x 10–27kg
  1 pound = 453.6g = 0.4536 kg
  
• For small time
  1 shake = 10–8s
  
• For large time

Lunar month: It is the time taken by the earth to complete one rotation about its axis with respect to sun.

1L.M.  = 27.3 days.

Solar day: It is the time taken by the earth to complete one rotation about its axis with respect to sun.

Sedrial day: It is the time taken by earth to complete one rotation on its axis with respect to distant star.

• For measuring pressure

1 bar = 1atm pressure = 105N/m2 = 760mmHg

1torr = 1 mmHg

1 poiseuille = 10 Poise

DIMENSIONS

The powers to which the fundamental units of mass, length and time must be raised to represent the physical quantity are called the dimensions of that physical quantity.

For example :

Force = mass × acceleration

 = mass ×  = [MLT–2]

Hence the dimensions of force are 1 in mass 1 in length and (– 2) in time.

DIMENSIONAL FORMULA

Unit of a physical quantity expressed in terms of M, L and T is called dimensional formula. It shows how and which of the fundamental quantities represent the dimensions.

For example, the dimensional formula of work is [ML2T–2]

DIMENSIONAL EQUATION

When we equate the dimensional formula with the physical quantity, we get the dimensional equation.

For example : Work = [ML2T–2]

CLASSIFICATION OF PHYSICAL QUANTITIES (ON THE BASIS OF DIMENSIONS)

DIMENSIONAL FORMULA OF SOME IMPORTANT PHYSICAL QUANTITIES

SHORT CUTS / TIME SAVING TECHNIQUES

• To find dimensions of a typical physical quantity which is involved in a number of formulae, try to use that formula which is easiest for you. For example if you want to find the dimensional formula of magnetic induction then you can use the following formulae

Out of these the easiest is probably the third one.

• If you have to find the dimensional formula of a combination of physical quantities, then instead of finding the dimensional formula of each, try to correlate the combination of physical quantities with a standard formula. For example, if you have to find the dimension of CV2, then try to use formula where E is energy of a capacitor.
• velocity of light in vacuum
• Dimensions of the following are same

[ML2T–2]

• Dimensions of the following are same

Force = Impulse / time

= q v B = q E

= Thrust

= weight  = energy gradient   [MLT–2]

• The dimension of RC = is same as that of time
• Dimensions of the following are same

Velocity =     [M°LT–1]

• Dimensions of the following are same

Frequency [M°L°T–1]

• Dimensions of the following are same

(E) Modulus of elasticity = Y (Young's modulus)

               = B (Bulk modulus)

   = η (Modulus of rigidity)

    = Stress

  = Pressure = [ML–1T–2]

• Dimensions of the following are same

Acceleration, retardation, centripetal acceleration, centrifugal acceleration, gravitational intensity/strength.       [M°LT–2]

• Dimensions of the following are same

Water equivalent, thermal capacity, entropy, Boltzmann's constant. [ML2T–2K–1]

KEEP IN MEMORY

The dimensional formula of

• all trigonometric ratio is [M0L0T0]
• x in ex is [M0L0T0]
• ex is [M0L0T0]
• x in log x is [M0L0T0]
• log x is [M0L0T0]

DIMENSIONAL ANALYSIS AND ITS APPLICATIONS

Principle of Homogeneity : Only those physical quantities can be added /subtracted/equated /compared which have the same dimensions.

USES OF DIMENSIONS

1. Conversion of one system of unit into another

Example : Convert a pressure of 106 dyne/cm2 in S.I units.

Sol. We know that 1N = 105 dyne ⇒ 1 dyne = 10–5 N

Also 1m = 100 cm ⇒ 1cm = 10–2 m

Now, the pressure 106 dyne/cm2 in SI unit is

2. Checking the accuracy of various formulae

Example : Check the correctness of the following equation dimensionally

where F = force, η  = coefficient of viscosity, A = area, gradient w.r.t distance, θ = angle of contact

Sol. L.H.S = force = [MLT–2]

R.H.S =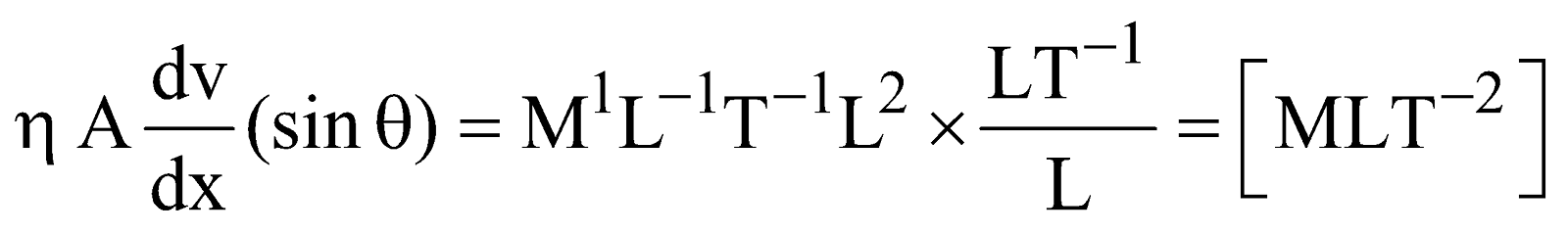

The equation is dimensionally correct.

3. Derivation of formula

Example : The air bubble formed by explosion inside water performed oscillation with time period T which is directly proportional to Pa db Ec where P is pressure, d is density and E is the energy due to explosion. Find the values of a, b and c.

Sol. Let us assume that the required expression for time period is T = K Pa db Ec

where K is a dimensionless constant.

Writing dimensions on both sides,

Equating the powers,

a +  b + c = 0 ....(1)

– a  – 3b + 2c = 0 ....(2)

– 2a – 2c = 1 ....(3)

Solving these equations,  we get,

a = , b = , c = .

LIMITATIONS OF DIMENSIONAL ANALYSIS

• No information about the dimensionless constant is obtained during dimensional analysis
• Formula cannot be found if a physical quantity is dependent on more than three physical quantities.
• Formula containing trigonometrical /exponential function cannot be found.
• If an equation is dimensionally correct it may or may not be absolutely correct.

SIGNIFICANT FIGURES

The number of digits, which are known reliably in our measurement, and one digit that is uncertain are termed as significant figures.

RULES TO DETERMINE THE NUMBERS OF SIGNIFICANT FIGURES

1. All non-zero digits are significant. 235.75 has five significant figures.
2. All zeroes between two non-zero digits are significant. 2016.008 has seven significant figures.
3. All zeroes occurring between the decimal point and the non-zero digits are not significant provided there is only a zero to left of the decimal point.  0.00652 has three significant figures.
4. All zeroes written to the right of a non-zero digit in a number written without a decimal point are not significant. This rule does not work if zero is a result of measurement. 54000 has two significant figures whereas 54000m has five significant figures.
5. All zeroes occurring to the right of a non-zero digit in a number written with a decimal point are significant. 32.2000 has six significant figures.
6. When a number is written in the exponential form, the exponential term does not contribute towards the significant figures. 2.465 × 105 has four significant figures.

KEEP IN MEMORY

• The significant figures depend upon the least count of the instrument.
• The number of significant figure does not depend on the units chosen.

ROUNDING OFF

• If digit to be dropped is less than 5 then preceding digit should be left unchanged.
• If digit to be dropped is more than 5 then one should raise preceding digit by one.
• If the digit to be dropped is 5 followed by a digit other than zero then the preceding digit is increased by one.
• If the digit to be dropped is 5 then the preceding digit is not changed if it is even.
• If digit to be dropped is 5 then the preceding digit is increased by one if it is odd.

ARITHMETICAL OPERATIONS WITH SIGNIFICANT FIGURES AND ROUNDING OFF

• For addition or subtraction, write the numbers one below the other with all the decimal points in one line. Now locate the first column from the left that has a doubtful digit. All digits right to this column are dropped from all the numbers and rounding is done to this column.  Addition subtraction is then done.

Example : Find the sum of 23.623 and 8.7 to correct significant figures.

Sol. Step-1 :- 23.623 + 8.7
Step-2 :-  23.6 + 8.7=32.3

• In multiplication and division of two or more quantities, the number of significant digits in the answer is equal to the number of significant digits in the quantity, which has minimum number of significant digits.

The insignificant digits are dropped from the result if they appear after the decimal point. They are replaced by zeroes if they appear to the left of the decimal point. The least significant digit is rounded off.

Example : 107.88 (5. S. F.) × 0.610 (3 S. F.) =  65.8068 ≅ 65.8

ACCURACY, PRECISION OF INSTRUMENTS AND ERRORS IN MEASUREMENTS

Accuracy and Precision are two terms that have very different meanings in experimental physics. We need to be able to distinguish between an accurate measurement and a precise measurement. An accurate measurement is one in which the results of the experiment are in agreement with the ‘accepted’ value.

Note:- This only applies to experiments where this is the goal like measuring the speed of light. A precise measurement is one that we can make to a large number of decimal places.

The following diagrams illustrate the meaning of terms accuracy and precision

In the above figure : The centre of the target represents the accepted value. The closer to the centre, the more accurate the experiment. The extent of the scatter of the data is a measure of the precision.

A - Precise and accurate

B - Accurate but imprecise

C - Precise but not accurate

D - Not accurate nor precise

When successive measurements of the same quantity are repeated there are different values obtained. In experimental physics it is vital to be able to measure and quantify this uncertainty. (The words "error" and "uncertainty" are often used interchangeably by physicists - this is not ideal - but get used to it!)

Error in measurements is the difference of actual or true value and measured value.

Error = True value – Measured value

KEEP IN MEMORY

1. Accuracy depends on the least count of the instrument used for measurement.
2. In the addition and subtraction operation, the result contains the minimum number of decimal places of the figures being used
3. In the multiplication and division operation, the result contains the minimum number of significant figures.
4. Least count (L.C.) of vernier callipers =  one MSD – one VSD

where MSD = mains scale division, VSD = vernier scale division

5. Least count of screw gauge  (or spherometer)
   where pitch is the ratio of number of  divisions moved on linear scale and number of rotations given to circular scale.
6. Pure number or unmeasured value do not have significant numbers
7. Change in the position of decimal does not change the number of significant figures. Similarly the change in the units of measured value does not change the significant figures.

COMMON ERRORS IN MEASUREMENTS

It is not possible to measure the 100% correct value of any physical quantity, even after measuring it so many times. There always exists some uncertainty, which is usually referred to as experimental error.

EXPERIMENTAL ERRORS

Random error : It is the error that has an equal chance of being positive or negative.

It occurs irregularly and at random in magnitude and direction. It can be caused

• by the lack of perfection of observer
• if the measuring instrument is not perfectly sensitive.

Systematic error :  It tends to occur in one direction either positive or negative. It occurs due to

• measuring instrument having a zero error.
• an instrument being incorrectly calibrated (such as slow- running-stop clock)
• the observer persistently carrying out a mistimed action (e.g., in starting and stopping a clock)

For measuring a particular physical quantity, we take a number of readings. Let the readings be X1, X2............,Xn. Then the mean value is found as follows

METHODS OF EXPRESSING ERROR

Absolute error :  It is the difference between the mean value and the measured value of the physical quantity.

|ΔX1|  = |Xmean–X1|  

..................................

..................................

|ΔXn|  = |Xmean–Xn|  

Mean absolute error:

ΔXmean or =

Relative error : It is the ratio of the mean absolute error and the value of the quantity being measured.

Percentage error : It is the relative error expressed in percent

Percentage error

TO FIND THE MAXIMUM ERROR IN COMPOUND QUANTITIES

SUM AND DIFFERENCE
We have to find the sum or difference of two values given as (a ± Δa) and (b ± Δb), we do it as follows

X ± ΔX = (a ± Δa) + (b ± Δb) = (a + b) ± (Δa + Δb)

⇒ X = a + b and ΔX = Δa + Δb in case of sum

And X = (a – b) and ΔX = Δa + Δb in case of difference.

PRODUCT AND QUOTIENT
We add the fractional or percentage errors in case of finding product or quotient.

If P = ab then

If  then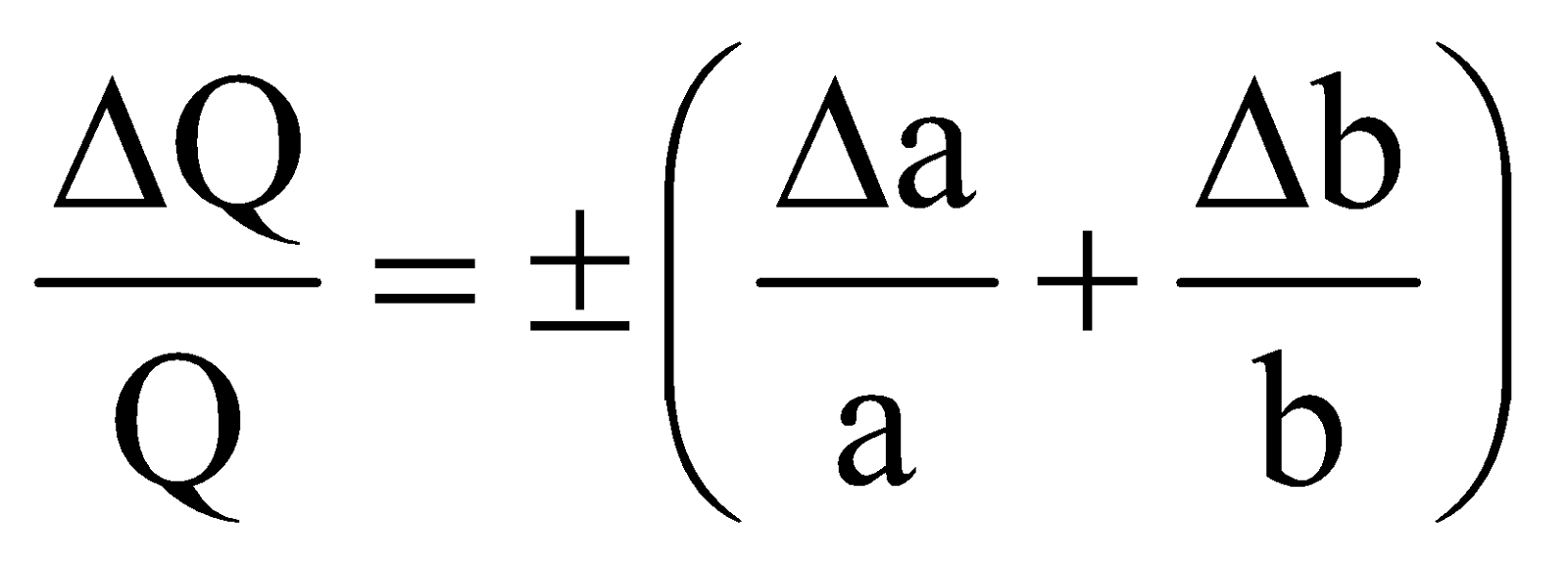

POWER OF A QUANTITY
If  x = an then

Example :   

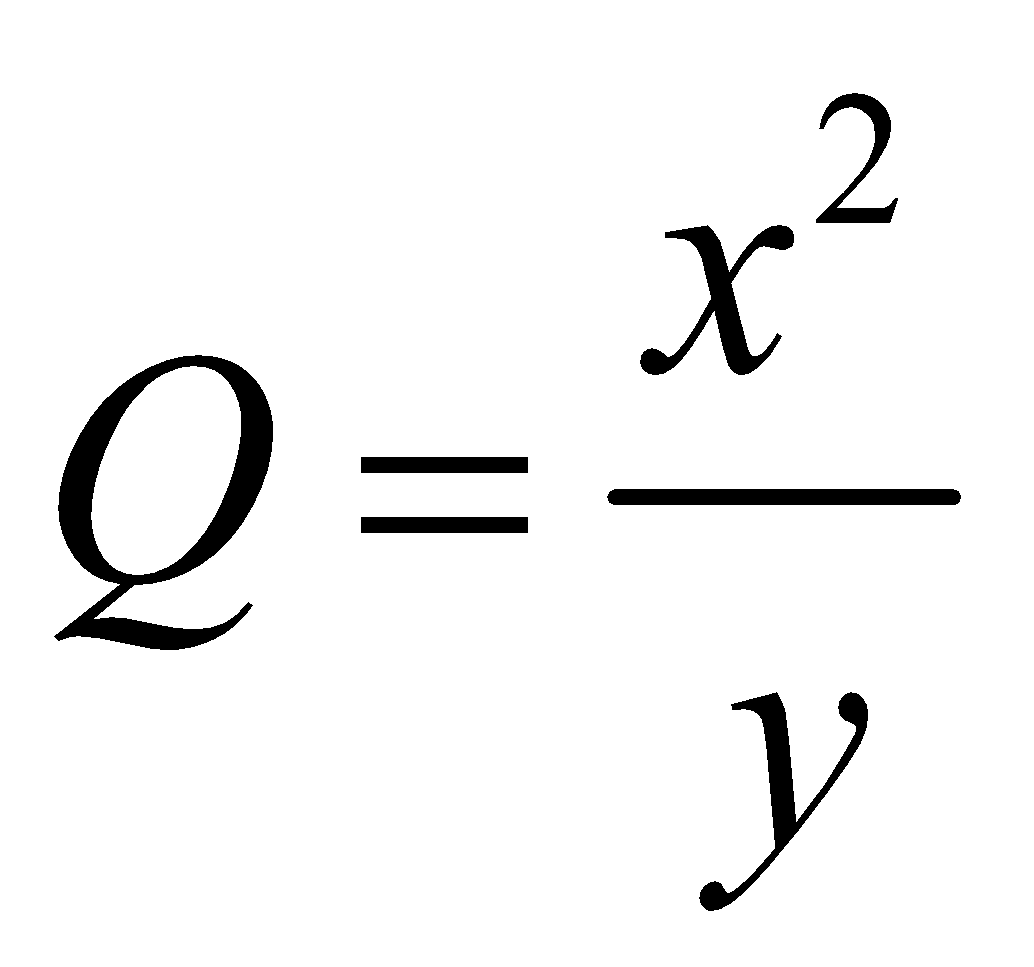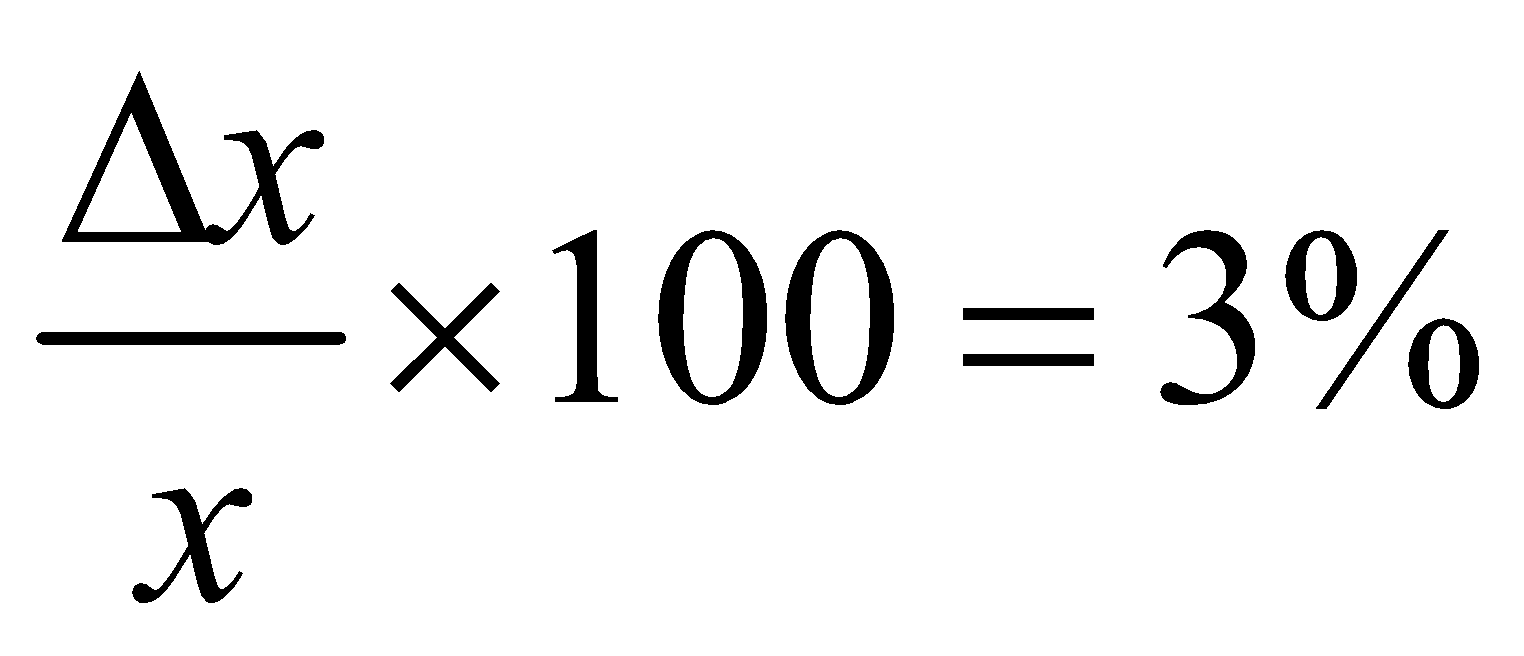For, If and

Then × 100 = (2 × 3 + 4)% = 10%

Similarly :

KEEP IN MEMORY

1. More the accuracy, smaller is the error.
2. Absolute error |ΔX| is always positive.
3. |ΔX| has the same dimensions as that of X.
4. If the least count of measuring instrument is not given and the measured value is given the least error in the measurement can be found by taking the last digit to be 1 and rest digit to be zero. For e.g. if the measured value of mass m = 2.03 kg then.
5. If a number of physical quantities are involved in an expression then the one with higher power contributes more in errors and therefore should be measured more accurately.
6. Relative error is a dimensionless quantity.
7. We are always interested in calculating the maximum possible error.

Physics Study Notes

• Physical World
• Units and Measurements
• Motion in a Straight Line
• Motion in a Plane
• Laws of Motion
• Work, Energy and Power
• System of particles and Rotational Motion
• Gravitation
• Mechanical Properties of Solids
• Mechanical Properties of Fluids
• Thermal Properties of Matter
• Thermodynamics
• Kinetic Theory of Gases
• Oscillations
• Waves
• Electric Charges and Fields
• Electrostatic Potential and Capacitance
• Current Electricity
• Moving Charges and Magnetism
• Magnetism and Matter
• Electromagnetic Induction
• Alternating Current
• Electromagnetic Waves
• Ray Optics and Optical Instruments
• Wave Optics
• Dual Nature of Radiation and Matter
• Atoms
• Nuclei
• Semiconductor Electronics : Materials, Devices and Simple Circuits
• Communication Systems
• Experimental Skills in Physics

Study Notes for JEE Main/JEE Advanced

Study Notes for NEET/AIIMS