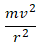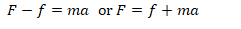Work power energy is the most important chapter when it comes to mechanics, for JEE (Advanced). The chapter is quite tricky and takes a lot of time and devotion on your part to understand and master. But this chapter is a complete gold medal for almost all the questions of the mechanics can be solved by the work power energy approach if you master this topic..
Q1.A mass of 2 kg slides down 1/4 circular track of radius 1 m. If the speed of mass at the bottom is 4 ms^(-1), work done by the frictional force is
Solution
Loss in PE=mgr=2×10×1=20 J
But gain in KE =1/2×2×4^2=16 J
Frictional work=16-20=-4 J
Loss in PE=mgr=2×10×1=20 J
But gain in KE =1/2×2×4^2=16 J
Frictional work=16-20=-4 J
Q3. A body of mass m is moving in a circle of radius r with a constant speedv. The force on the body is mv^2/r and is force in moving the body over half the circumference of the circle?
Solution
Zero, because there is no displacement in the direction of force. Centripetal force does not do work
Zero, because there is no displacement in the direction of force. Centripetal force does not do work
Q4. A heavy weight is suspended from a spring. A person raises the weight till the spring becomes slack. The work done by him isW. The energy stored in the stretched spring was E. What will be the gain in gravitational potential energy?
Solution
Total gravitational energy gained is Work done+ energy released by the spring = W+E
Total gravitational energy gained is Work done+ energy released by the spring = W+E
Q5.Two particles are interacting only because of conservation forces. They complete round trips, ending at the point from where they started. Over this trip
Solution
Factual
Factual
Q8.A block of mass m is moving with a constant acceleration a on a rough plane. If the coefficient of friction between the block and the ground is μ, the power delivered by the external agent after a time t from the beginning is equal to
Q9.Work done by a conservative force on a system is equal to
Solution
We know that dU=-dW Where dU is the change in potential energy And dW is the work done by conservative forces Hence, work done by conservation forces on a system is equal to the negative of the change in potential energy
We know that dU=-dW Where dU is the change in potential energy And dW is the work done by conservative forces Hence, work done by conservation forces on a system is equal to the negative of the change in potential energy