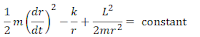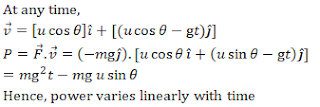Work Energy and Power-Quiz-14

WORK ENERGY AND POWER Quiz-14

Dear Readers,

Work power energy is the most important chapter when it comes to mechanics, for JEE (Advanced). The chapter is quite tricky and takes a lot of time and devotion on your part to understand and master. But this chapter is a complete gold medal for almost all the questions of the mechanics can be solved by the work power energy approach if you master this topic..

Q1.

•  0 J
•  +600 J
•  -600 J
•  +1600 J

Solution

f=3/10 mg
W=-fs =-3/10 mgS
=-3/10×200×10 J=-600 J

Q2.In the above questions, the work done by frictional force is

•  +1600 J
•  -1600 J
•  +3200 J
•  -3200 J

Solution

Work done by friction force is equal to negative of the work done by the coolies

Q3.  

•  Only statement I is true
•  Only statement II is true
•  Only I and III are true
•  Only II and III are true

Solution

Q4. A spring is compressed between two toy carts of masses m_1 andm_2. When the toy carts are released, the spring exerts on each toy cart equal and opposite forces for the same small timet. If the coefficients of friction μ between the ground and the toy carts are equal, then the magnitude of displacements of the toy carts are in the ration

•  s1/s2 =m2/m1
•  s1/s2 =m1/m2
•  s1/s2 =(m2/m1 )^2
•  s1/s2 =(m1/m2 )^2

Solution

Minimum stopping distance =s
Work done against the friction =W=μmgs
Initial momentum gained by both toy carts will be same
Because same force acts for same time Initial kinetic energy of the toy cart =(p^2/2m) Therefore, (μmgsp^2)/2m or s=(p^2/(2μgm^2 ))
For the two toy carts, momentum is numerically the same. Further μ and g are the same for the toy carts. So s1/s2 =(m2/m1 )^2

Q5.Let r be the distance of a particle from a fixed point to which it is attracted an inverse square law force given by F=k/r^2 (k= constant). Let m be the mass of the particle and L be its angular momentum with respect to the fixed point. Which of the following formulae is correct about the total energy of the system

•  
  
•  
  
•  
  
•  
  

Solution
 

Q6. Two trucks A andB, one loaded and the other unloaded, are moving and have same kinetic energy. The mass of A is double that ofB. Brakes (providing same retarding force) are applied to both and are brought to rest. If the distance converted by A before coming to rest is s1 and that of B is s2, then

•  s1=s2
•  s1=2s2
•  2s1=s2
•  s1=4s2

Solution

Work done by braking force=change in KE -Fs=0-KEi ⇒s=(KEi)/F KEi and F are same for both, Hence, s is also same for both

Q7.A force F=-K(yi+xj) (where K is a positive constant) acts on a particle moving in the xy-plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particles is

•  -2 Ka^2
•  2Ka^2
•  -Ka^2
•  Ka^2

Solution

Q8.A lorry and a car moving with the same K.E. are brought to rest by applying the same retarding force, then

•  Lorry will come to rest in a shorter distance
•  Car will come to rest in a shorter distance
•  Both come to rest in a same distance
•  None of the above

Solution

Stopping distance =(kinetic energy)/(retarding force)⇒s=1/2 (mu^2)/F
If lorry and car both possess same kinetic energy and retarding force is also equal then both come to rest in the same distance

Q9. The energy required to accelerate a car from rest to 10 ms^(-1) is E. What energy will be required to accelerate the car from 10 ms^(-1) to 20 ms^(-1)?

•  E
•  3E
•  5E
•  7E

Solution

Q10. A particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force

•  Varies linearly with time
•  Is constant throughout
•  Is negative for complete path
• None of these

Solution