Important topics for Thermodynamics has been designed in such a way that it offers very practical and application-based learning to further make it easier for students to understand every concept or topic by correlating it with the day-to-day experiences.
Q1. The efficiency of a Carnot engine working between source temperature T_1 and sink temperature T_2 is η=1-T_2/T_1 . The efficiency cannot be 100% as we cannot maintain T_2=0. Coefficient of performance of a refrigerator working between the same two temperature is
Coefficient of performance T_2/(T_1-T_2 )=(1-η)/η
The efficiency of a Carnot engine working between 27℃ and -73℃ is:
Q2.The changes in pressure and volume of a gas when heat content of the gas remains constant are called adiabatic changes. The equation of such changes is pV^γ= constant. The changes must be sudden and the container must be perfectly insulting to disallow any exchange of heat with the surrounding. In such changes, dQ=0. As per first law of thermodynamics, dQ=dU+W=0. Therefore, dU=-dW.
A gas in a container is compressed suddenly. Its temperature would:
Q3. Three moles of an ideal gas (C_p=7R/2) at pressure P_A and temperature T_A are isothermally expanded to twice the original volume. The gas is then compressed at constant pressure to its original volume. Finally the gas is heated at constant volume to its original pressure P_A
Which of the graphs shown in Fig. represents the P-V diagram for the complete process?:
Q4. Two moles of an ideal gas at volume V, pressure 2 P and temperature T undergo a cyclic process ABCDA as shown in Fig. The volume (V_B) of the gas in state B is
Q5.Two moles of a monoatomic ideal gas occupy a volume Vat 27°C. The gas is expanded adiabatically to volume 2√2 V. Gas constant R=8.3 JK^(-1) mol^(-1)The final temperature of the gas is
Q6. A sample of 2 kg of monoatomic helium (assumed ideal) is taken through the process ABC and another sample of 2 kg of the same gas is taken through the process ADC as shown in Fig. The molecular mass = 4 and R = 8.3 J K^(-1) mol^(-1). The temperature of state A is
Q7.One mole of an ideal monoatomic gas is taken round the cyclic process ABCA as shown in Fig. :
The work done by the gas is
Q8.Two moles of an ideal mono-atomic gas is taken through a cycle ABCA as shown in the P-T diagram (Fig). During the process AB, pressure and temperature of the gas vary such that PT=K, where K is a constant
Constant K is given by:
Q9.A monoatomic ideal gas of 2 moles is taken through a cyclic process starting from A as shown in Fig:
The temperature of the gas at point B is
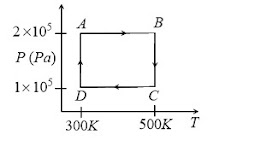
Q10. Two moles of helium gas are taken over the cycle ABCDA, as shown in the P-T diagram:
Assuming the gas to be ideal the work done on the gas in taking it from A to B is