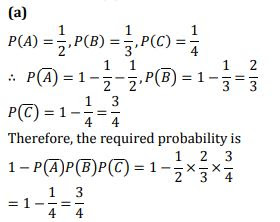Probability is an important topic in JEE advanced
examination. In this exam, probability carries weightage of
7% of questions. With focused practice good marks can be
fetched from this topic
.
Q1. Three integers are chosen at random from the set of first 20 natural numbers. The chance that their product is a multiple of 3 is:
Q2.A purse contains 2 six-sided dice. One is a normal fair die, while the other has two 1’s , and two 5’s. A die is picked up and rolled. Because of some secret magnetic attraction of the unfair die, there is 75% chance of picking the unfair die and a 25% chance of picking a fair die. The die is rolled and shows up the face 3.The probability that a fair die was picked up is:
Q3. A problem in mathematics is given to three students A,B,C and their respective probability of solving the problem is 1/2, 1/3 and 1/4. Probability that the problem is solved is:
Q4. A fair die is thrown 20 times. The probability that on the 10th throw, the fourth six appears is:
Q5. Mr. A lives at origin on the Cartesian plane and has his office at (4, 5). His friend lives at (2,3) on the same plane. Mr. A can go to his office travelling one black at a time either in the +y or +x direction. If all possible paths are equally likely then the probability that Mr. A passed his friends house is (shortest path for any event must be considered):
Q6. There are two urns A and B. Urn A contains 5 red, 3 blue and 2 white balls, urn B contains 4 red, 3 blue and 3 white balls. An urn is choosen at random and a ball is drawn. Probability that the ball drawn is red is:
Q7. In a game a coin is tossed 2n+m times and a player wins if he does not get any two consecutive outcomes same for atleast 2n times in a row. The probability that player wins the game is:
Q8.Let A and B be events. Suppose P(A)=0.4,P(B)=p and P(P∪B)=0.7. The value of p for which A and B are independent is:
Q9.If a and b are chosen randomly from the set consisting of numbers 1, 2, 3, 4, 5, 6 with replacement. Then the probability that lim(x→0)〖[(ax+bx)/2]2/x 〗=6 is:
Q10. Four die are thrown simultaneously. The probability that 4 and 3 appear on two of the die given that 5 and 6 have appeared on other two die is: