Permutations and Combinations is one of the most important chapters of Algebra in the JEE syllabus and other engineering exams. For JEE Mains, it has 4% weightage and for JEE Advanced, it has 5% weightage..
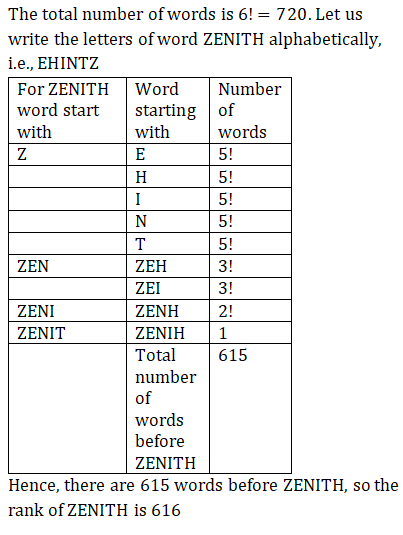
Q1. The letters of word ‘ZENITH’ are written in all possible ways. If all these words are written in the order of a dictionary, then the rank of the word ‘ZENITH’ is
Q2.Let there be circles in a plane. The value of for which the number of radical centres is equal to the number of radical axes is (assume that all radical axes and radical centre exist and are different)
Solution
For a radical centre, 3 circles are required. The total number or radical centres is nC3. The total number or radical axis is nC2. Now, nC2 = nC3 => n = 5
For a radical centre, 3 circles are required. The total number or radical centres is nC3. The total number or radical axis is nC2. Now, nC2 = nC3 => n = 5
Q3. In a class tournament, all participants were to play different games with one another. Two players fell ill after having played three games each. If the total number of games played in the tournament is equal to 84, the total number of participants in the beginning was equal to
Q4. There are four letters and four directed envelopes. The number of ways in which all the letters can be put in the wrong envelope is
Solution
There is concept of derangement. The required number is
4![1 - 1/1! + 1/2! - 1/3! + 1/4!] = 9
There is concept of derangement. The required number is
4![1 - 1/1! + 1/2! - 1/3! + 1/4!] = 9
Q5.Ten IIT and 2 DCE students sit in a row. The number of ways in which exactly 3 IIT students sit between 2 DCE students is
Solution
Three IIT students who will be between the IIT students can be selected in 10C3 ways. Now, two DCE students having three IIT students between them can be arranged in 2! x 3! ways. Finally, a group of above five students and the remaining seven students together can be arranged in 8! ways. Hence, total number of ways is 10C3 x 2! x 3! x 8!
Three IIT students who will be between the IIT students can be selected in 10C3 ways. Now, two DCE students having three IIT students between them can be arranged in 2! x 3! ways. Finally, a group of above five students and the remaining seven students together can be arranged in 8! ways. Hence, total number of ways is 10C3 x 2! x 3! x 8!
Q6. A variable name in certain computer language must be either an alphabet or an alphabet followed by a decimal digit. The total number of different variable names that can exist in that language is equal to
Solution
Total number of variables if only alphabet is used is 286. Total number of variables if alphabets and digits both are used is 26 x 10. Hence, the total number of variables is 26(1 + 10) = 286
Total number of variables if only alphabet is used is 286. Total number of variables if alphabets and digits both are used is 26 x 10. Hence, the total number of variables is 26(1 + 10) = 286
Q7.A student is allowed to select at most n books from a collection of (2n + 1) books. If the total number of ways in which he can select at least one book is 63, then the value of n is
Q8.Let Tn denote the number of triangles, which can be formed using the vertices of a regular polygon of n sides. If Tn+1 - Tn = 21, then n equals
Q9.The number of seven digit integers, with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only, is
Solution
There are two possible cases
Case I Five 1’s, one 2’s, one 3’s
Number of numbers = 7!/5! = 42
Case II Four 1’s, three 2’s
Number of numbers = 7!/4!3! = 35
Total number of numbers 42 + 35 = 77
There are two possible cases
Case I Five 1’s, one 2’s, one 3’s
Number of numbers = 7!/5! = 42
Case II Four 1’s, three 2’s
Number of numbers = 7!/4!3! = 35
Total number of numbers 42 + 35 = 77
Q10.The number of ordered pairs of integers (x,y) satisfying the equation x2 + 6x + y2 = 4
Solution
(x + 3)2 + y2 = 13
x + 3 = ±3 or x + 3 = ±3, y = ±2
(x + 3)2 + y2 = 13
x + 3 = ±3 or x + 3 = ±3, y = ±2