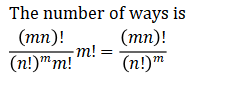Permutations and Combinations-Quiz-3

Permutations and Combinations Quiz-3

Dear Readers,

Permutations and Combinations is one of the most important chapters of Algebra in the JEE syllabus and other engineering exams. For JEE Mains, it has 4% weightage and for JEE Advanced, it has 5% weightage..

Q1. 2m white counters and 2n red counters are arranged in a straight line with (m + n) counters on each side of a central mark. The number of ways of arranging the counters, so that the arrangements are symmetrical with respect to the central mark, is

•  ^m+nC_m
•  ^2m+2nC_2m
•  1/2 x (m + n)!/m!n!
•  None of these

Solution

Q2.The number of even divisors of the number N = 12600 = 2³3²5²7 is

•  72
•  54
•  18
•  None of these

Solution
Number of even divisors is equal to number of ways in which one or more ‘2’, zero more ‘3’, zero or more ‘5’ and zero or more ‘7’ can be selected, and is given by (3)(2 + 1)(2 + 1)(1 + 1) = 54

Q3.  The total number not more than 20 digits that are formed by using the digits 0,1,2,3 and 4 is

•  5²⁰
•  5²⁰ - 1
•  5²⁰ + 1
•  None of these

Solution
Each position can be filled in 5 ways. Hence, the total number of numbers is 5²⁰

Q4. There are (n + 1) white and (n + 1) black balls each set numbered 1 to n. The number of ways in which the balls can be arranged in a row so that the adjacent balls are of different color is

•  (2n + 2)!
•  (2n + 2)! x 2
•  (n + 1)! x 2
•  2{(n + 2)!}²

Solution
Since the balls are to be arranged in a row so that the adjacent balls are of different colors, we can therefore begin with a white ball or a black ball. If we begin with a white ball. We find that n + 1 white balls numbered 1 to n + 1 can be arranged in a row in (n + 1)! ways. Now n + 2 places are created among n + 1 white balls which can be filled by n + 1 black balls in (n + 1)! ways So, the total number of arrangements in which adjacent balls are of different colors and first ball is a white ball is (n + 1)! x (n + 1)! = [(n + 1)!]². But we can begin with a black ball also. Hence, the required number of arrangements is 2[(n + 1)!]²

Q5.If m parallel lines in a plane are intersected by a family of n parallel lines, the number of parallelograms that can be formed is

•  1/4(mn(m - 1)(n - 1))
•  1/2(mn(m - 1)(n - 1))
•  1/4(m²n²)
•  None of these

Solution
The number of selection of two parallel lines from m lines is ^mC₂
The number of selection of two parallel lines from n lines is ⁿC₂
Hence, the number of parallelograms lines is ^mC₂ X ⁿC₂ = 1/4(mn(m - 1)(n - 1))

Q6. A person predicts the outcome of 20 cricket matches of his home team. Each match can result in a either win, loss or tie for the home team. Total number of ways in which he can make the predictions so that exactly 10 predictions are correct is equal to

•  ²⁰C₁₀ X 2¹⁰
•  ²⁰C₁₀ X 3²⁰
• ²⁰C₁₀ X 3¹⁰
•  ²⁰C₁₀ X 2²⁰

Solution
Matches whose predictions are correct can be selected in ²⁰C₁₀ ways. Now each wrong prediction can be made in 2 ways. Thus, the total number of ways is ²⁰C₁₀ X 2¹⁰

Q7.The number of ways in which we can distribute mn students equally among m sections is given by

•  (mn)!/n!
•  (mn)!/(n!)^m
•  (mn)!/(m!n!)
•  (mn)^m

Solution

Q8.The number of possible outcomes in a throw of ordinary dice in which at least one of the dice shows an odd number is

•  6ⁿ - 1
•  3ⁿ - 1
•  6ⁿ - 3ⁿ
•  None of these

Solution
The total number of ways is 6 x 6 x ... to n times = 6ⁿ. The total number of ways to show only even numbers is 3 x 3 x ... to n times = 3ⁿ. Therefore, the required number of ways is 6ⁿ - 3ⁿ

Q9.The total number of ways of selecting six coins out of 20 one rupee coins, 10 fifty-paise coins and 7 twenty-five paise coins is

•  28
•  56
•  ³⁷C₆
•  None of these

Solution
Since the total number of selections of r things from n things where each thing can be repeated as many times as one can is ^n+r-1C_r. Therefore the required number is ^3+6-1C₆ = 28

Q10. A seven-digit number without repetition and divisible by 9 is to be formed by using seven digits out of 1,2,3,4,5,6,7,8,9. The number of ways in which this can be done is

•  9!
•  2(7!)
•  4(7!)
• None of these

Solution
Sum of 7 digits is a multiple of 9. Sum of numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 is 45; so two left digits should also have sum of 9. The pairs of left numbers are (1,8),(2,7),(3,6),(4,5). With each pair left number of 7-digit number is 7!. So with all 4 pairs, total number is 4 X 7!