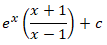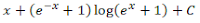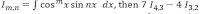Integrals- Quiz 1

Integrals Quiz-1

Dear Readers,

Important topics for Maths has been designed in such a way that it offers very practical and application-based learning to further make it easier for students to understand every concept or topic by correlating it with the day-to-day experiences.

Q1. 

 is equal to

•  π/4
•  π/2
•  π
•  none of these

Solution
Put x=tan⁡θ ∴dx=sec^2⁡θdθ When x=∞,tan⁡θ= ∞,∴θ=π/2

Q2.

•  1/2 [sec^2 x-tan⁡x ]+c
•  1/2 [x sec^2 x-tan⁡x ]+c
•  1/2 [x sec^2 x+tan⁡x ]+c
•  1/2 [sec^2 x+tan⁡x ]+c

Solution
∫x sin⁡x sec^3x dx  =∫x sin⁡x 1/(cos^3 x) dx  =∫x tan⁡x sec^2 x dx  =x∫sec⁡x(sec⁡x tan⁡x )dx-∫[sec⁡x(sec⁡x tan⁡x )dx ]dx+C   =x sec^2⁡x/2-∫sec^2⁡x/2 dx+C  =x sec^2⁡x/2-tan⁡x/2+C

Q3.The value of

is

•  0
•  3
•  4
•  1

Solution

Q4. 

•  
  
•  
  
•  
  
•  
  

Solution
I=∫√(e^x-1 ) dx  Let e^x-1=t^2⇒e^x dx=2t dt ⇒dx=2t/(t^2+1) dt  ⇒I=∫t 2t/(t^2+1) dt=∫(2t^2)/(t^2+1) dt  =∫(2(t^2+1)-2)/(t^2+1) dt=∫2dt-∫2dt/(t^2+1)  =2t-2 tan^(-1)⁡t+C  =2√(e^x-1)-2 tan^(-1)⁡√(e^x-1)+C

Q5.

•  
  
•  
  
•  
  
•  None of these

Solution
 ∫(e^x (x^2+1))/(x+1)^2 dx  =∫(e^x (x^2-1+2))/(x+1)^2 dx  =∫e^x [(x-1)/(x+1)+2/(x+1)^2 ]dx  =∫e^x [f(x)+f^' (x)]dx,where f(x)=(x-1)/(x+1) and  f^'(x)=2/(x+1)^2   =e^x ((x-1)/(x+1))+C 

Q6. 

•  2
•  -2
• 1/2
•  -1/2

Solution

Q7.  The value of the definite integral 

•  cos⁡2+cos⁡4
•  cos⁡2-cos⁡4
•  sin⁡2+sin⁡4
•  sin⁡2-sin⁡4

Solution

Q8. If I =

then I equals:

•  
  
•  
  
•  
  
•  None of these

Solution
I=-e^(-x) log⁡(e^x+1)+∫(e^(-x) e^x)/(e^x+1) dx  = -e^(-x) log⁡(e^x+1)+∫e^(-x)/(e^(-x)+1) dx  = -e^(-x) log⁡(e^x+1)-log⁡(e^(-x)+1)+C  = -e^(-x) log⁡(e^x+1)-log⁡(1+e^x )+x+C  = -(e^(-x)+1) log⁡(e^x+1)+x+C

Q9. If f(x) is monotonic differentiable function on [a,b], then

•  bf(a)-af(b)
•  bf(b)-af(a)
•  f(a)+f(b)
•  Cannot be found

Solution
∫_a^bf(x)dx=[xf(x)]a^b-∫_a^bxf^'(x)dx (1) Now, put f(x)=t ∴ x=f^(-1 ) (t) and f^' (x)dx=dtand adjust the limits Therefore, ∫_a^bf(x)dx=[bf(b)-af(a) ]-∫_(f(a))^(f(b))f^(-1) (t)dt by (1) ∴∫_a^bf(x) +∫_(f(a))^(f(b))f^(-1) (x)dx=bf (b)-af(a)

Q10. If I_(m,n)=

is equal to

•  Constant
•  
  
•  
  
• cos⁡7x-cos⁡4x+C

Solution
I_4,3=∫cos^4⁡x sin⁡3xdx  Integrating by parts, we have  I_4,3=-cos⁡3x cos^4⁡x /3-4/3 ∫cos^3⁡x sin⁡x cos⁡3xdx  But sin⁡x cos⁡3x=-sin⁡2x+sin⁡3x cos⁡x , so  I_4,3=-cos⁡x cos^4⁡x /3+4/3 ∫cos^3⁡x sin⁡2xdx-4/3 ∫cos^4⁡x sin⁡3xdx+C   =-cos⁡3x cos^4⁡x/3+(4/3) I_3,2(-4/3) I_4,3+C Therefore, 7/3 I_4,3(-4/3) I_3,2=-cos3x cos^3⁡x /3+C Or 7I_4,3-4I_3,2=-cos⁡3x cos^4⁡x+C