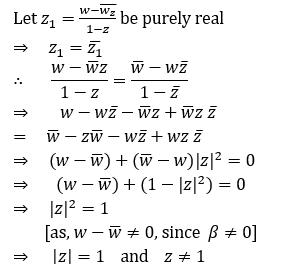Complex Numbers and Quadratic Equations-Quiz-9

Complex Number & Quadratic Equation Quiz-9

Dear Readers,

Complex numbers and quadratic equations is a segment of maths that deals with crucial theorems and concepts along with various formulae. It comprises of linear and quadratic equations along with roots related to the complex number's set (known as complex roots)..

Q1. The set of values of a for which (a - 1)x^2 - (a + 1)x + a - 1 ≥ 0 is true for all x≥2

•  (-∞ , 1)
•  (1 , 7/3)
•  (7/3 , ∞)
•  None of these

Solution
(c) Given,
(a - 1)x^2 - (a + 1)x + a - 1 ≥ 0
⇒ a(x^2 - x + 1) - (x^2 + x + 1) ≥ 0
⇒ a ≥ ( x^2 + x + 1 )/( x^2 - x + 1 )
= 1 + 2x/( x^2 - x + 1 )
= 1 + 2/( x + 1/x - 1) (1)
Let y = x + 1/x. Now, y is increasing in [2,∞). Hence,
1 + 2/( x + 1/x - 1)∈(1 , 7/3]
For all x ≥ 2, Eq. (1) should be true. Hence, a > 7/3

Q2.If w = α + iβ, where β ≠ 0 and z ≠ 1, satisfies the condition that (( w - w ̅z )/( 1 - z ) ) is purely real, then the set of values of z is

•   |z| = 1, z ≠ 2
•  |z| = 1 and z ≠ 1
•  z= ̅z
•  None of these

Solution
(b)

Q3.  The number of points of intersection of two curves y = 2 sin⁡x and y = 5x^2 + 2x + 3 is

•  0
•  1
•  2
•   ∞

Solution
(a)
Minimum value of 5x^2 + 2x + 3 is
-D/4a = -( (2)^2 - 4(5)(3) )/( 4(5) ) >2
Where maximum value of 2 sin⁡x is 2. Therefore, the two curves do not meet at all

Q4. 

•  n
•  n^2
•  n^n
•  0

Solution
(a)
Clearly,

Q5. If one root of the equation ax^2 + bx + c = 0 is square of the other, then a( c - b )^3 = cX, where X is

•  a^3 - b^3
•  a^3+b^3
•  (a - b)^3
•  None of these

Solution
 (c)
If one root is square of the other root of the equation ax^2 + bx + c = 0, then
β = α^2 ⇒ α^2 + α = -b/a and α^2 a = c/a
By eliminating α, we get
b^3 + ac^2 + a^2 c = 3abc
Which can be written in the form a(c - b)^3 = c(a - b)^3
Alternative solution:
Let the roots be 2 and 4. Then the equation is x^2 - 6x + 8 = 0
Here obviously,
X = ( a(c - b)^3 )/c = ( 1(14)^3 )/8 = 14/2 × 14/2 × 14/2 = 7^3
Which is given by ( a - b )^3 = 7^3

Q6. Let x,y,z,t be real numbers x^2 + y^2 = 9 , z^2 + t^2 = 4 and xt - yz = 6. Then the greatest value of P = xz is

•  2
•  3
• 4
•  6

Solution
(b)
x = 3 cos⁡θ ; y = 3sin⁡θ
z = 2cos⁡ϕ ; t = 2sin⁡ϕ
∴ 6cos⁡θ sin⁡ϕ - 6sin⁡θ cos⁡[ϕ=6]
⇒sin⁡[(ϕ - θ)] = 1
⇒ϕ = 90° + θ
⇒P = xz = -6sin⁡θ cos⁡θ = -3sin⁡2θ
⇒P_max = 3

Q7. Let λ ∈ R , the origin and the non-real roots of 2z^2 + 2z + λ = 0 form the three vertices of an equilateral triangle in the Argand plane then λ is

•  1
•  2/3
•  2
•  -1

Solution


(b)
2z^2 + 2z + λ = 0
Let the roots be z_1 , z_2. Then,
z_1 + z_2 = -1 and z_1 z_2 = λ/2
0 , z_1 , z_2 form, an equilateral triangle
∴ z_1^2 + z_2^2 = z_1 z_2
⇒ (z_1 + z_2 )^2 = 3z_1 z_2
⇒ 1 = 3λ/2
⇒ λ = 2/3

Q8. The number of values of k for which [x^2 - (k - 2)x +k^2 ]× [x^2 + kx + (2k - 1)] is a perfect square is

•  2
•  1
•  0
•  None of these

Solution
(b)
Verify by selecting particular values of a and b
Let a = -9 and b = 4. Then,
√a √b = √( -9 ) √4 =( 3i )( 2 ) = 6i
From option (a), we have
-√( |a|b ) = -√(|-9|×4) = -√36 = -6
From option (b), we have
√( |a|bi ) = √( |-9|×4 ) i = 6i

Q9. Let p(x) = 0 be a polynomial equation of the least possible degree, with rational coefficients, having ∛7+∛49 as one of its roots. Then the product of all the roots of p(x) = 0 is

•  56
•  63
•  7
•  49

Solution
(a)
x = ∛7 + ∛49
⇒ x^3 = 7 + 49 + 3∛7 ∛49 ( ∛7 + ∛49 ) = 56 + 21x
⇒ x^3 - 21x - 56 = 0
Therefore, the product of roots is 56

Q10. The number of real solutions of the equation |x|^2 - 3|x| + 2 = 0 is

•  4
•  1
•  2
• 0

Solution
(a)
|x|^2 - 3|x| + 2 = 0
⇒ ( |x| - 2) (|x| - 1) = 0
⇒ |x| = 1 or 2
⇒x = ±1 , ±2
Hence, there are four real solutions