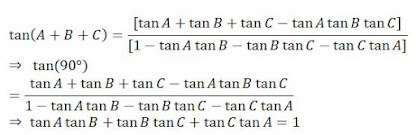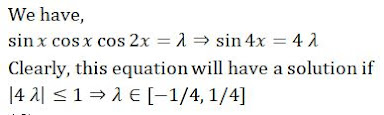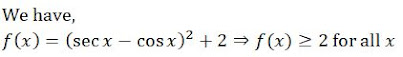Admissions,1,Alternating Current,60,AP EAMCET 2020,1,Basic Maths,2,BCECE 2020,1,best books for iit jee,2,best coaching institute for iit,1,best coaching institute for iit jee preparation,1,best iit jee coaching delhi,1,best iit jee coaching in delhi,2,best study material for iit jee,4,BITSAT Registration 2020,1,Blog,62,books for jee preparation,1,books recommended by iit toppers,3,Capacitance,3,CBSE,1,CBSE accounts exam,1,CBSE boards,1,CBSE NEET,9,cbse neet 2019,3,CBSE NEET 2020,1,cbse neet nic,1,Centre of Mass,2,Chemistry,58,Class 12 Physics,15,coaching for jee advanced,1,coaching institute for iit jee,2,Collision,2,COMEDK UGET 2020 Application Form,1,COMEDK UGET 2020 Exam Form,1,COMEDK UGET news,1,CUCET 2020,2,Current Electricity,4,CVR college,1,Digestion and Absorption Notes PDF,1,Electromagnetic Induction,3,Electronics,1,Electrostatics,3,Energy,1,Engineering & Medical,1,Fluid Mechanics,4,Gravitation,2,GUJCET 2020 Application Form,1,Heat,4,iit admission,1,iit advanced,1,iit coaching centre,3,iit coaching centre in delhi,2,iit coaching classes,2,iit coaching in delhi,1,iit coaching institute in delhi,1,iit entrance exam,1,iit entrance exam syllabus,2,iit exam pattern,2,iit jee,5,iit jee 2019,3,iit jee advanced,2,iit jee books,3,iit jee coaching,2,iit jee exam,3,iit jee exam 2019,1,iit jee exam pattern,3,iit jee institute,1,iit jee main 2019,2,iit jee mains,3,iit jee mains syllabus,2,iit jee material,1,iit jee online test,3,iit jee practice test,3,iit jee preparation,6,iit jee preparation in delhi,2,iit jee preparation time,1,iit jee preparation tips by toppers,2,iit jee question paper,1,iit jee study material,3,iit jee study materials,2,iit jee syllabus,2,iit jee syllabus 2019,2,iit jee test,3,iit preparation,2,iit preparation books,5,iit preparation time table,2,iit preparation tips,2,iit syllabus,2,iit test series,3,IITJEE,100,Important Biology Notes for NEET Preparation,1,IPU CET,1,JEE Advanced,83,jee advanced exam,2,jee advanced exam pattern,1,jee advanced paper,1,JEE Books,1,JEE Coaching Delhi,3,jee exam,3,jee exam 2019,6,JEE Exam Pattern,2,jee exam pattern 2019,1,jee exam preparation,1,JEE Main,85,jee main 2019,4,JEE Main 2020,1,JEE Main 2020 Application Form,2,JEE Main 2020 news,2,JEE Main 2020 Official Answer Key,1,JEE Main 2020 Registration,1,JEE Main 2020 Score,1,JEE Main application form,1,jee main coaching,1,JEE Main eligibility criteria,3,jee main exam,1,jee main exam 2019,3,jee main online question paper,1,jee main online test,3,JEE Main Paper-2 Result,1,jee main registration,2,jee main syllabus,2,JEE mains 2020,1,jee mains question bank,1,jee mains test papers,3,JEE Mock Test,2,jee notes,1,jee past papers,1,JEE Preparation,2,jee preparation in delhi,1,jee preparation material,4,JEE Study Material,1,jee syllabus,6,JEE Syllabus Chemistry,1,JEE Syllabus Maths,1,JEE Syllabus Physics,1,jee test series,3,KCET - 2020,1,Kinematics,1,Latest article,5,Latest Articles,61,Latest News,34,latest news about neet exam,1,Laws of Motion,2,Magnetic Effect of Current,3,Magnetism,3,MHT CET 2020,2,MHT CET 2020 exam schedule,1,Modern Physics,1,NCERT Solutions,15,neet,3,neet 2019,1,neet 2019 eligibility criteria,1,neet 2019 exam date,2,neet 2019 test series,2,NEET 2020,2,NEET 2020 Application Form,1,NEET 2020 Eligibility Criteria,1,NEET 2020 Registration,1,neet application form,1,neet application form 2019 last date,1,Neet Biology Syllabus,1,Neet Books,3,neet eligibility criteria,3,neet exam 2019,7,neet exam application,1,neet exam date,1,neet exam details,1,neet exam pattern,6,neet exam pattern 2019,2,neet examination,1,neet mock test 2019,1,Neet Notes,3,Neet Online Application Form,3,neet online test,2,neet past papers,1,neet physics syllabus,1,neet practice test,2,NEET preparation books,1,neet qualification marks,1,NEET question paper 2019,1,neet question papers,1,neet registration,1,Neet Study Material,3,neet syllabus,6,neet syllabus 2019,5,NEET Syllabus 2020,1,neet syllabus chemistry,1,neet syllabus for biology,1,neet syllabus for physics,1,neet test series,1,neet ug 2019,2,news,5,online study material for iit jee,1,Optical Instruments,1,Physics,110,physics books for iit jee,1,Power,1,Practical Physics,1,Quiz,5,Ray Optics,1,Rotational Motion,3,SHM,3,Simple Harmonic Motion,3,study materials for iit jee,1,Study Notes,110,study notes for iit jee,1,Thermodynamics,4,TS EAMCET Notification,2,Units and Dimensions,1,UPSEE 2020,1,UPSEE 2020 Application Form,2,UPSEE EXAM,1,Vectors,2,VITEE Application form,1,Wave Motion,3,Wave Optics,1,WBJEE 2020 Admit Card,1,WBJEE 2020 Answer Key,1,Work,1,